一种大规模MIMO系统的上行功率控制方法及装置与流程

本发明涉及无线通信技术领域，更具体地，涉及一种大规模mimo系统的上行功率控制方法及装置。

背景技术：

多入多出(multiple-inputmultiple-output，mimo)技术是指在发射端和接收端分别使用多个发射天线和接收天线，使信号通过发射端与接收端的多个天线传送和接收，从而改善通信质量。它能充分利用空间资源，通过多个天线实现多发多收，在不增加频谱资源和天线发射功率的情况下，可以成倍的提高系统信道容量，显示出明显的优势，被视为下一代移动通信的核心技术。

大规模mimo(massivemimo)时分双工系统作为一种新颖的蜂窝网络结构成为当前的研究热点，在大规模mimo系统中，基站端有数量巨大的低功率小天线，天线数目远远超过同时调度的单天线用户设备数量，基站和用户设备之间通过时分双工进行通信。大规模天线阵列提供了很高的阵列增益和很高的空间分辨率。在较好的传播条件下，线性大规模mimo系统可以有效地消除小区内的干扰和噪声。

目前，现有的大规模mimo系统在功率分配时，将总功率平均分配给所有用户设备，这样不能充分挖掘大规模mimo系统在单用户功率控制方面的潜力；并且大规模mimo系统内所有用户设备的和速率也未达到最大，没有发挥大规模mimo系统的优势。

技术实现要素：

针对上述的技术问题，本发明提供一种大规模mimo系统的上行功率控制方法及装置。

第一方面，本发明实施例提供一种大规模mimo系统的上行功率控制方法，包括：s1，根据系统和速率上界建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；s2，根据所述凸性优化函数，获取小区内用户设备的功率分配结果。

其中，在所述s1之前还包括：s0，根据获取的小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和大尺度衰落系数，获取系统和速率上界。

其中，所述s0包括：s01，根据小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备发射功率和大尺度衰落系数，获取本小区基站的接收信号；s02，根据所述基站接收的信号获取信道状态矩阵，并根据所述信道状态矩阵获取所述小区内各用户设备的信噪比；s03，根据所述信噪比及詹森不等式，获得所述系统和速率上界。

其中，所述s1中的将所述非凸性优化函数转化为凸性优化函数包括：s11，根据对数下界不等式和变量指数变换，将所述非凸性优化函数转化为半非凸性优化函数；s12，通过一阶泰勒级数展开，将所述半非凸性优化函数转化为所述凸性优化函数；其中，所述半非凸性优化函数为目标函数为凸、约束条件为非凸的函数。

其中，所述s2包括：s21，获取所述凸性优化函数的解，并根据所述解获取所述非凸性优化函数的解；s22，根据所述非凸性优化函数的解更新对数下界不等式的参数，然后再次基于获取的所述凸性优化函数的解，获取所述非凸性优化函数的解；s23，直到获取的所述非凸性优化函数第t次与第t-1次的解的差的范数平方小于预设阈值时，得到小区内用户设备的功率分配结果，其中t≥2。

其中，所述信噪比为：

其中，γlk为第l小区内的第k个用户设备的信噪比；plk为第l小区内的第k个用户设备的发射功率；为信道估计误差的自相关矩阵；为小区间干扰的自相关矩阵；为噪声的自相关矩阵；为信道状态矩阵；为第i小区的第k个用户设备到第l个小区基站的路损和阴影衰落效应，即大尺度衰落系数；pik为第i小区内的第k个用户设备的发射功率。

相应地，所述和速率上界为：

其中，为信道估计带来的速率损失，t为各信道相干间隔，为用户设备发射的导频序列长度，

其中，所述非凸性优化函数为：

所述凸性优化函数为：

第二方面，本发明提供一种大规模mimo系统的上行功率控制装置，包括：获取模块，用于根据小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备发射功率和大尺度衰落系数，获取系统和速率上界；转化模块，用于根据所述和速率上界，建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；分配模块，用于根据所述凸性优化函数，获取小区内用户设备的功率分配结果。

第三方面，本发明提供一种大规模mimo系统的上行功率控制装置，包括：至少一个处理器；以及与所述处理器通信连接的至少一个存储器，其中，所述存储器存储有可被所述处理器执行的程序指令，所述处理器调用所述程序指令能够执行如权利要求1至7任一所述的方法。

第四方面，本发明实施例提供一种非暂态计算机可读存储介质，所述非暂态计算机可读存储介质存储计算机指令，所述计算机指令使所述计算机执行如权利要求1至7任一所述的方法。

本发明提供的一种大规模mimo系统的上行功率控制方法及装置，通过根据系统和速率上界建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；然后根据所述凸性优化函数，获取小区内用户设备的功率分配结果。这样在满足本小区内用户设备速率需求的同时，使得大规模mimo系统内所有用户设备的速率之和达到最大，充分发挥了大规模mimo系统的潜力。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作一简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的大规模mimo系统的上行功率控制方法的流程图；

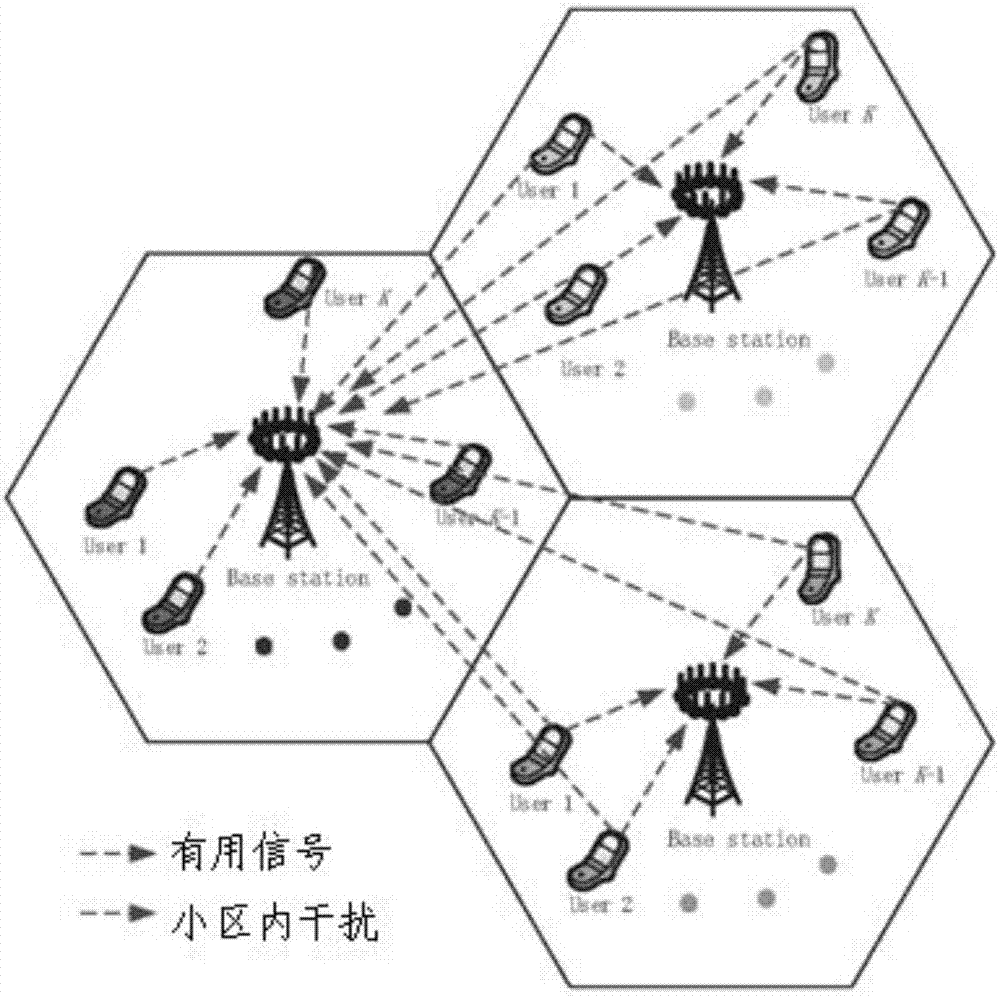
图2为图1所述的大规模mimo系统的上行功率控制方法中的大规模mimo系统的结构示意图；

图3为图1所述的大规模mimo系统的上行功率控制方法的根据凸性优化函数获取小区内用户设备的功率分配结果的流程图；

图4为本发明另一实施例提供的大规模mimo系统的上行功率控制方法中系统和速率随基站天线数的变化图；

图5为本发明另一实施例提供的大规模mimo系统的上行功率控制方法中优化后的速率增益随基站天线数的变化图；

图6为本发明另一实施例提供的大规模mimo系统的上行功率控制方法中本小区内用户设备的总发射功率随基站天线数的变化图

图7为本发明实施例提供的大规模mimo系统的上行功率控制装置的结构框图；

图8为本发明另一实施例提供的大规模mimo系统的上行功率控制装置的结构框图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

图1为本发明实施例提供的大规模mimo系统的上行功率控制方法的流程图，如图1所示，该方法包括：s1，根据系统和速率上界建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；s2，根据所述凸性优化函数，获取小区内用户设备的功率分配结果。

其中，mimo(multiple-inputmultiple-output)技术指在发射端和接收端分别使用多个发射天线和接收天线，使信号通过发射端与接收端的多个天线传送和接收，从而改善通信质量。它能充分利用空间资源，通过多个天线实现多发多收，在不增加频谱资源和天线发射功率的情况下，可以成倍的提高系统信道容量，显示出明显的优势、被视为下一代移动通信的核心技术。

在本发明实施例中，以一个具有多个小区的大规模mimo系统为例，系统中由六边形形状的l个小区组成，每个小区的中心有一个基站，基站有m根天线，且假定每个小区内有k个单天线用户，满足大规模mimo系统条件，即m＞＞k。另外，假定每个小区使用相同的频率资源，即频率再使用因子为1，整个系统操作在时分双工(timedivisionduplexing，tdd)模式。图2为一个有3个小区的大规模mimo系统，假定在上行接收，每个基站预先不知道对用户的信道状态信息(csi)，并采用破零(zf)滤波处理。csi的获取通过导频训练获得，即在每个信道相干间隔(t)的开始，每个用户都向所在的基站发射一个长度为τ的导频序列，这里显然满足t＞τ。小区内的用户使用正交的导频序列集，且正交导频序列集在所有相邻的小区中重复使用。

其中，凸函数就是一个定义在某个向量空间的凸子集c(区间)上的实值函数。

具体地，在控制大规模mimo系统的上行功率时，根据mimo系统的和速率上界建立非凸性优化函数，为了较方便的获得非凸性优化函数的解，将该非凸性优化函数转化为凸性优化函数。对凸性优化函数进行求解，根据求得的凸性优化函数的解获取到非凸性优化函数的解，即可以获取到小区内用户设备的功率分配结果。

本发明实施例与现有技术相比，通过根据系统和速率上界建立非凸性优化函数，并将非凸性优化函数转化为凸性优化函数，然后通过求解凸性优化函数获取到非凸性优化函数的解，进而得到小区内用户设备的功率分配结果，这样在满足本小区内用户设备速率需求的同时，使得大规模mimo系统内所有用户设备的速率之和达到最大，充分发挥了大规模mimo系统的潜力。

在上述实施例的基础上，在所述s1之前还包括：s0，根据获取的小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和大尺度衰落系数，获取系统和速率上界。

其中，大尺度衰落系数是指系统内所有用户设备到本小区基站的路损和阴影衰落效应对应的参数。

具体地，在根据系统和速率上界建立非凸性优化函数之前，需要先获取到系统的和速率上界。在每个小区的用户设备同时向各自所在对的小区基站发射导频训练序列后，各个小区的基站都会获取到小区内用户设备的发射功率，并根据发射功率计算出大尺度衰落系数，然后系统内其他小区基站会将小区内用户设备的发射功率和大尺度衰落系数反馈至本小区。然后根据本小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和所有用户设备到本小区基站的大尺度衰落系数，可以获取到系统的和速率上界。

在本发明实施例中，通过根据本小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和所有用户设备到本小区基站的大尺度衰落系数，获取到系统的和速率上界，这样保证了在系统的速率之和达到最大时进行小区内用户设备的功率分配，充分发挥的大规模mimo系统的潜能。

在上述实施例的基础上，所述s0包括：s01，根据小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备发射功率和大尺度衰落系数，获取本小区基站的接收信号；s02，根据所述基站接收的信号获取信道状态矩阵，并根据所述信道状态矩阵获取所述小区内各用户设备的信噪比；s03，根据所述信噪比及詹森不等式，获得所述系统和速率上界。

其中，信道状态信息(channelstateinformation，csi)在无线通信领域就是通信链路的信道属性，它描述了信号在每条传输路径上的衰弱因子，即信道增益矩阵h中每个元素的值，如信号散射(scattering)，环境衰弱(fading，multipathfadingorshadowingfading)，距离衰减(powerdecayofdistance)等信息。csi可以使通信系统适应当前的信道条件，在多天线系统中为高可靠性高速率的通信提供了保障。

其中，信噪比英文名称叫做snr或s/n(signal-noiseratio)，又称为讯噪比，是指一个电子设备或者电子系统中信号与噪声的比例。这里面的信号指的是来自设备外部需要通过这台设备进行处理的电子信号，噪声是指经过该设备后产生的原信号中并不存在的无规则的额外信号(或信息)，并且该种信号并不随原信号的变化而变化。

其中，詹森不等式是关于凸性(convexity)的不等式，它给出积分的凸函数值和凸函数的积分值间的关系。其中，凸性是非常好的性质，在最优化问题里面，线性和非线性不是本质的区别，只有凸性才是。如果最优化的函数是凸的，那么局部最优就意味着全局最优，否则无法推得全局最优。

具体地，在根据获取的小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和系统内所有用户设备到本小区基站的大尺度衰落系数，获取系统和速率上界时，先根据小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和所有用户设备到本小区基站的大尺度衰落系数，获取本小区基站的接收信号。然后对本小区基站的接收信号进行处理得到所有用户设备到本小区基站的信道矩阵，并根据基站接收的信号和该信道矩阵可以获得本小区内各用户设备的信噪比。最后通过应用詹森不等式和根据该信噪比，以获得系统的和速率上界。

在本发明实施例中，通过根据获得的信噪比和应用詹森不等式获得系统的和速率上界，这样在满足小区内用户设备的功率需求的同时，可以使系统的速率之和达到最大，充分体现了大规模mimo系统的优势。

在上述实施例的基础上，所述s1中的将所述非凸性优化函数转化为凸性优化函数包括：s11，根据对数下界不等式和变量指数变换，将所述非凸性优化函数转化为半非凸性优化函数；s12，通过一阶泰勒级数展开，将所述半非凸性优化函数转化为所述凸性优化函数；其中，所述半非凸性优化函数为目标函数为凸、约束条件为非凸的函数。

其中，对数下界不等式是指有最小值的对数不等式。

其中，指数变换是指将变量用其对应的指数替换。

其中，泰勒级数用无限项连加式——级数来表示一个函数，这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(sirbrooktaylor)的名字来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做迈克劳林级数，以苏格兰数学家科林·麦克劳林的名字命名。泰勒级数在近似计算中有重要作用。

具体地，在根据获取的和速率上界建立好非凸性欧化函数之后，需要将建立的非凸性优化函数转化为凸性优化函数，首先根据对数下界不等式和变量的指数变换，将非凸性优化函数转化为半非凸性优化函数，即目标函数为凸、约束条件为非凸的函数。然后再通过一阶泰勒级数展开，将半非凸性优化函数转化为凸性优化函数，这样就可以通过使用离线优化工具包求解凸性优化函数，例如，用cvx获取凸性优化函数的解，然后根据获取的凸性优化函数的解来得到非凸性优化函数的解，进而获得本小区内用户设备的功率分配结果。

在本发明实施例中，通过根据对数不等式、变量的指数变换以及一阶泰勒级数展开，将非凸性优化函数转化为凸性优化函数，这样可以较简单和快速的得到凸性优化函数的解，进而得到非凸性优化函数的解，达到简化求解过程的目的，并且使得获得本小区内用户设备的功率分配更准确。

在上述实施例的基础上，结合图3，所述s2包括：s21，获取所述凸性优化函数的解，并根据所述解获取所述非凸性优化函数的解；s22，根据所述非凸性优化函数的解更新对数下界不等式的参数，然后再次基于获取的所述凸性优化函数的解，获取所述非凸性优化函数的解；s23，直到获取的所述非凸性优化函数第t次与第t-1次的解的差的范数平方小于预设阈值时，得到小区内用户设备的功率分配结果，其中t≥2。

其中，范数是数学中的一种基本概念，在泛函分析中，范数是一种定义在赋范线性空间中函数，满足相应条件后的函数都可以被称为范数。

具体地，在根据系统和速率上界建立好非凸性优化函数，并将非凸性优化函数转化为凸性优化函数之后，先求解转化得到的凸性优化函数，并根据获得的凸性优化函数的解得到之前非凸性优化函数的解。然后根据获取的非凸性优化函数的解更新对数下界不等式中的参数，然后根据更新后的对数下界不等式再次对凸性优化函数进行求解，并根据求得的解再次对凸性优化函数进行求解。这样一直循环直到获取的非凸性优化函数第t次与第t-1次的解的差的范数平方小区预设阈值，其中t≥2，例如，非凸性优化函数第t次与第t-1次的解的差的范数平方小于10^-6，则可以结束循环，将该第t次获得的非凸性优化函数的解作为最终解，即可以得到小区内用户设备的功率分配结果。

在本发明实施例中，通过不断的更新对数不等式的参数，并且对每次获得的非凸性优化函数的解进行检测，直到相近两次非凸性优化函数的解满足条件时，才停止更新对数不等式，并将最后一次非凸性优化函数的解作为本小区内用户设备的功率分配结果，这样可以提高本小区内用户设备功率分配的准确性，使得功率分配更合理。

在上述实施例的基础上，所述信噪比为：

其中，γlk为第l小区内的第k个用户设备的信噪比；plk为第l小区内的第k个用户设备的发射功率；为信道估计误差的自相关矩阵；为小区间干扰的自相关矩阵；为噪声的自相关矩阵；为估计的信道矩阵；为第i小区的第k个用户设备到第l个小区基站的路损和阴影衰落效应，即大尺度衰落系数；pik为第i小区内的第k个用户设备的发射功率；相应地，所述和速率上界为：

其中，为信道估计带来的速率损失，t为各信道相干间隔，为用户设备发射的导频序列长度，

具体地，在获取到小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备发射功率和大尺度衰落系数之后，则小区内的基站接收的数据为：

其中，pl是对角矩阵，其对角元素[pl]k,k＝plk表示第l个小区内的第k个用户的数据发射功率，si是第i个小区内k个用户发射的数据向量，满足nl表示第l个小区基站m根天线上接收到的独立加性高斯噪声向量，假定噪声的功率已被归一化，即

利用估计的信道矩阵，基站执行破零(zeroforcing，zf)检测后输出的信号可写成，

这里的为zf滤波器，i1,i2,i3定义如下，

其中，i1,i2和i3分别代表由信道估计误差带来的干扰，小区间干扰和噪声。它们的均值都为零，自相关矩阵计算如下，

根据基站输出的信号可以获得第l小区内的第k个用户设备的信噪比，用γlk表示，即

其中，是第i小区的第k个用户设备到第l个小区基站的路损和阴影衰落效应，即大尺度衰落系数。

根据香农公式，于是第l个小区遍历的上行可达和速率可表示为：

其中，是信道估计带来的速率损失。

由于估计矩阵的复杂分布和信噪比公式中的矩阵求逆操作，导致γlk的分布将更加复杂，再加上和速率公式中的对数操作，使得求解精确的和速率rl变得非常困难。于是，我们可以求出精确速率的边界。

定义则γlk可以表示成由估计理论和随机矩阵理论可知，是服从自由度为m的维希特(wishart)分布，即

其中，根据wishart分布的变换性质，即

变换矩阵m是秩为k的k×m维矩阵，当m取特殊的形式时，可知是服从δllkx～w1(m-k+1,δllk)分布，其相应的概率密度函数为：

其中，m-k+1是形状参数影响着分布的形状不仅包括位置移动及伸展/收缩，δllk是速率参数，该值越大概率密度函数的形状拉伸的越厉害，该值越小概率密度的形状函数越集中。

利用f(x)＝log2(1+x)是x的凹函数的结论，并对和速率表达式应用詹森不等式，可以得到，

因为则函数x＞0也是关于x的凹函数，再次使用詹森不等式，e(γlk)可进一步放大为：

由(11)和(12)可得：

根据(10)式容易计算出e(x)＝(m-k+1)δllk。将这个结果带入(13)，可得到上行速率的上界：

这里，和

其中，在信道矩阵估计阶段，每个小区的用户设备同时都向各自所在的小区基站发射长度为τ的导频训练序列，用符号表示每个小区内k个用户的正交导频序列集，满足φ^hφ＝ik。用户设备发射完导频序列后，第l小区的基站接收的训练信号可以表示成，

其中，yp,l的下标p表示导频(pilot)信号，下标l指第l个小区；表示第i小区内的k个用户到第l个小区基站的信道矩阵；表示用户到基站的瑞利衰落效应，其中的元素都是均值为零、方差为1的独立同分布(i.i.d.)复高斯随机变量，即对角阵表示第i小区内的k个用户到第l个小区基站的路损和阴影衰落效应，并假定是已知的；对角阵q的对角元素[qi]k,k＝qik表示第i小区内的第k个用户发射的导频功率；矩阵nl表示第l个小区基站的m根天线上接收的噪声，满足

为了估计信道状态信息(channelstateinformation，csi)，基站首先对接收到的信号乘以正交的导频序列集φ并进行预处理可得，

由于用户设备位置独立，所以gll的各列向量gllk，k＝1,2,…,k也是独立的，因而可以取出gll中的某个列向量单独进行估计，于是

ek表示第k个元素为1，其余元素为0的k×1维的列向量。注意：由于正交变换不影响元素的分布特性，故上式中省略了nl后的正交矩阵φ。

利用mmse估计理论，可得gllk的mmse估计结果为：

因此，要估计的信道矩阵可以写成如下形式

类似地，还能容易地得出第i个小区的k个用户到第l个小区基站的信道矩阵即

其中，

根据估计理论，估计向量和误差矢量是相互独立的，并分别服从分布和其中，

在上述实施例的基础上，所述非凸性优化函数为：

所述凸性优化函数为：

具体地，在根据系统和速率上界建立好非凸性优化函数时，对于其他小区固定而已知的发射功率，通过下行控制优化用户的发射功率以获得最大小区吞吐量，则非凸性优化函数可建模为，

由于上面的目标函数

具有凸差分(d.c.)结构，因此该非凸性优化函数关于pl1,pl2,…,plk是非凸的，则通过下面的办法转化成凸性优化函数。

将下面的对数下界不等式，

log2(1+z)≥ξlog2z+μ(24)

当近似常数作如下选择时，上面的不等式在z＝z0时将非常的紧，

为此，定义将和带入到zk可得：

应用(24)式和变量指数变换到问题非凸性优化函数可松弛为下面的半非凸性优化函数

其中，

上式中的ck定义为ξk和μk由(25)式和(26)式分别给出。

给定ξk和μk，由于(29)式中第一项是线性函数和凹函数之和(注意log-sum-exp是凸函数)，因此，问题的目标按说关于变量是凹函数。很明显，(28)式中的第一个约束条件也是凸函数，但第二个约束条件还是非凸的，此时得到的是半非凸性优化函数。则对第二个约束条件的左边用一阶泰勒级数展开，通过迭代逼近该约束条件，于是可转换为下面的凸性优化函数

其中，是第t-1次的迭代结果，因而在第t次迭代求解时是已知的。显然，已经是一个标准的凸性优化函数了，可以用离线优化工具包，比如cvx进行有效求解。

通过不断地进行迭代，直到非凸性优化函数的解收敛，例如，非凸性优化函数第t次与第t-1次的解的差的范数平方小于预设阈值，例如，预设阈值为10^-6。这样就可以得到最终的非凸性优化函数的解，即可以得到本小区用户设备的功率分配结果。

以下对本发明实施例进行举例说明，但不限制本发明的保护范围。假设有3个小区，每个小区有5个用户设备，以第1个小区为例，设第1个小区的用户设备到本基站的大尺度衰落系数为β11＝[1,0.8,0.4,0.1,0.05]，第2个小区的用户设备到第1个小区的基站的大尺度衰落系数为β12＝10^-2×[0.17,0.15,0.14,0.105,0.08]，第3个小区的用户设备到第1个小区的基站的大尺度衰落系数为β13＝10^-2×[0.18,0.16,0.13,0.07,0.06]。第1个小区内的每个用户设备发射功率都为30db，第2个和第3个小区的5个用户设备的发射功率取相同的一组值，即5db，10db，15db，20db，30db。每个用户的最大发射功率为50db，最小发射功率为5db。可以得到，如图4所示的系统和速率随基站天线数的变化情况；如图5所示的优化功率控制获得的速率增益随基站天线数的变化情况；如图6所示的优化功率控制后的用户设备的发射功率之和随基站天线数的变化情况。

图4中带星号的虚线是每个用户设备以30db的功率发射时获得的仿真和速率；菱形的虚线是每个用户设备以30db的功率发射时得到的可达和速率的上界；带星号的实线是通过本发明实施例提供的方法进行优化功率控制以后的得到的仿真和速率，带菱形的实线是通过本发明实施例提供的方法进行优化功率控制以后的得到的可达和速率上界。从图4可以看出，无论是否进行功率控制，增加基站天线数都可以提高系统的可达和速率；且得到的闭式的可达和速率上界表达式在整个基站天线范围内都能精确地匹配仿真得到的速率；基站对用户设备的发射功率进行优化控制以后，在考虑的基站天线数范围内都可以使得系统获得的可达和速率得到明显地提高。

图5给出了速率增益δr＝r^opt-r随基站天线数的变化情况，其中，r^opt表示基站对用户设备进行优化功率控制后系统获得的可达和速率，r表示基站对用户设备没有进行优化功率控制，即基站都按照30db发射功率时系统获得的可达和速率。从图5可以明显地看出，当基站的天线数增加时，功率控制的优势也越来越明显，即功率控制后获得的速率增益随着基站天线数的增加也在不断增加。

图6给出了优化功率控制后第l个小区所有用户设备总的发射功率随基站天线数的变化情况。从图6可以看出，随着基站天线数的增加，所有用户设备总的发射功率在不断减小，特别是基站天线数比较小时，增加天线数会使总的发射功率得到明显降低。应该注意的是，即使是总的发射功率降低了，从图5可知，系统获得的可达和速率是在增大的，所以说，使用本发明实施例提供的功率控制方法，不仅可以提高系统的可达和速率，还可以减少用户设备的辐射功率。

图7为本发明实施例提供的大规模mimo系统的上行功率控制装置的结构框图，如图7所示，该功率控制装置包括：获取模块701、转化模块702及分配模块703。

具体地，在控制大规模mimo系统的上行功率时，每个小区的用户设备同时向各自所在对的小区基站发射导频训练序列，然后获取模块701会获取到小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率以及所有用户设备到本小区基站的大尺度衰落系数。获取模块701则根据本小区内用户设备的发射功率、系统内其他小区基站反馈的用户设备的发射功率和大尺度衰落系数，可以获取到系统的和速率上界。然后转化模块702根据和速率上界建立非凸性优化函数，且将非凸性优化函数转化为凸性优化函数。最后分配模块703对凸性优化函数进行求解，进而获取到非凸性优化函数的解，即得到小区内用户设备的功率分配结果。

本发明实施例与现有技术相比，通过转化模块根据系统和速率上界建立非凸性优化函数，并将非凸性优化函数转化为凸性优化函数，然后通过分配模块求解凸性优化函数获取到非凸性优化函数的解，进而得到小区内用户设备的功率分配结果，这样在满足本小区内用户设备速率需求的同时，使得大规模mimo系统内所有用户设备的速率之和达到最大，充分发挥了大规模mimo系统的潜力。

图8为本发明另一实施例提供的大规模mimo系统的上行功率控制装置的结构框图，如图8所示，该识别装置包括：处理器801、存储器802和总线803；

其中，处理器801和存储器802通过总线83完成相互间的通信；所述处理器801用于调用所述存储器802中的程序指令，以执行上述各方法实施例所提供的方法，例如包括：根据系统和速率上界建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；根据所述凸性优化函数，获取小区内用户设备的功率分配结果。

在另一实施例中，提供一种非暂态计算机可读存储介质，所述非暂态计算机可读存储介质存储计算机指令，所述计算机指令使所述计算机执行上述各方法实施例所提供的方法，例如包括：根据系统和速率上界建立非凸性优化函数，并将所述非凸性优化函数转化为凸性优化函数；根据所述凸性优化函数，获取小区内用户设备的功率分配结果。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。