一种降低FBMC‑OQAM系统PAPR的低复杂度SLM算法的利记博彩app
本发明涉及一种通信技术的优化方法,尤其涉及一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法。
背景技术:
滤波器组多载波(FBMC)是一种频谱效率高、实现复杂度尚可、无需同步的多载波传输方案。偏移正交幅度调制(OQAM)可以消除FBMC系统中各子带交叠将带来的载波间干扰(ICI)。FBMC与OQAM结合,具有很多OFDM技术没有的优势,例如优秀的频率定位和较低的功率谱密度(PSD)旁瓣等,比OFDM更适合5G无线接入技术(RAT)。FBMC-OQAM系统日益成为无线电波即将到来的5G无线接入技术(RAT)的领跑者。像正交频分复用(OFDM)一样,FBMC-OQAM存在较高的PAPR,这将降低高功率放大器(HPA)的效率,导致信号失真、频谱扩展、系统性能下降。所以,FBMC-OQAM系统PAPR减小技术是目前研究的一个重大课题。
PAPR减小技术可以分为以下几种:限幅技术、编码技术、加扰技术、自适应预失真技术和离散傅立叶变换(DFT)扩频技术。限幅技术是在峰值附近采用限幅或非线性饱和来减少PAPR,包括块缩放技术、削波和滤波技术、傅里叶映射技术、以及判决辅助重建技术;编码技术是选择能够使PAPR最小或PAPR减小的码字,可以使用Colay互补序列、M序列和Hadamard码;加扰技术是对输入数据进行加扰,并发射具有最小PAPR的数据块;自适应预失真技术可以补偿OFDM系统中HPA的非线性效应。
FBMC-OQAM由于其重叠结构而无法运用OFDM中很好降低PAPR的方法。目前,有学者讨论了PAM符号的FBMC-OQAM系统降低PAPR的方案,但是这些方案仅限于PAM符号且BER性能较差。还有学者实现了运用迭代补偿的剪切方案减小FBMC-OQAM系统的PAPR,但是该系统需要设计一个复杂的接收机来满足剪切噪音的补偿。多模块联合优化(MBJO)技术和滑动窗口语音预留(SWTR)技术目前也都运用于FBMC-OQAM系统的PAPR降低中,但是它们有一个较高的复杂度。有学者提出了一种重叠的选择性映射(OSLM)方法,提出连续符号之间的独立性假设不成立,考虑了FBMC-OQAM的自然重叠,但是有一个巨大的内存和计算复杂度。后来又有学者提出一种色散选择性映射(DSLM)方法,这种方法与传统的SLM类似,同时考虑了FBMC-OQAM的重叠性,解决了FBMC-OQAM信号时间色散的性质,但是计算的是[0,4T]区间内的PAPR值,复杂度比较高。基于上述陈述,本发明在SLM算法的基础上进行改进,合理利用FBMC信号的重叠性质和功率分布规律,提出了一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,即LD-SLM算法。
技术实现要素:
由对FBMC-OQAM信号的平均功率仿真可知,每个信号周期的能量主要集中分布在[T,3T]内,本发明提出了一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,即LD-SLM算法。传统的SLM算法只计算[0,T]区间内所有点数PAPR值,在此区间搜索最小PAPR值,这是无法匹配FBMC-OQAM信号重叠性质的,结果导致不能有效降低FBMC-OQAM系统PAPR,本发明在传统的SLM的基础上进行改进,根据FBMC-OQAM信号功率分布集中在中间[T,3T](T为符号周期)区间的特点,计算集中在区间[T,3T]内符号的PAPR值,找出区间[T,3T]内最小PAPR值来选择最佳旋转符号。
一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,包括以下步骤:
S1、首先初始化旋转矢量,生成U个长度为N的相位旋转矢量:
其中:n∈[0,N-1],u∈[0,U-1];
S2、将当前数据块与旋转矢量相乘,每个输入数据块Xm都与U个不同的旋转矢量相乘:
其中:·表示矩阵点对点乘法;
S3、对信号进行采样、滤波和调制,由于FBMC-OQAM信号的重叠性质,需要考虑当前数据块之前的信号,从而得到如下信号:
其中:m∈[0,2π],t∈[0,(m+1/2)T+4T];
S4、根据下列公式计算信号xu(t)的PAPR,计算区间为Tc;
S5、根据PAPR计算的结果,选择最优旋转方案,得到当PAPR值最小时的旋转矢量编号,即并将umin作为边信息保存在USI=[USI umin]中;
S6、最后更新输入,根据umin选择最佳旋转矢量,与当前数据块相乘,更新输入信号矩阵然后返回步骤S2中,对下一个信号周期的信号Xm+1重复上述步骤,直至m=M-1。
所述LD-SLM算法只计算集中在区间[T,3T]内符号的PAPR值,找出区间[T,3T]内最小PAPR值来选择最佳旋转符号,不是SLM算法的[0,T]区间,也不是DSLM的[0,4T]区间。
本发明提出的一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,在优化算法复杂度的同时,具有降低系统PAPR的特性,既考虑到了FBMC-OQAM信号的自然重叠部分,又缩短了搜索时间,比DSLM算法在时间复杂度上更有优势,与DSLM算法相比,由于计算PAPR值之前步骤相同,即输入的FBMC信号经过采样和滤波,通过滤波器需要2N(Lh+1)(MT0+Lh-1)个实数乘法,接着将每个数据块与生成的旋转矢量相乘,需要UN(Lh+T/2)个复数乘法;对当前数据块和之前数据块进行调制需要UN((2m+1)T/2+4T)个复数乘法;计算PAPR值时需要2UNTc个实数乘法和NUTc个实数加法,求最大值需要NUTc次查找比较,求均值和取对数运算分别需要1次实数除法和UNTc次对数运算,以及1次实数乘法,此处将1次实数乘法、实数加法、实数除法、对数运算和一次查找比较运算均记作1次实数运算;因此,主要比较计算PAPR时的区别,即对公式的实现算法不同,因此DSLM算法的计算复杂度为:CDSLM=16MNUT+4MNUT+M,即CDSLM=20MNUT+M;本发明提出的LD-SLM算法,采样、滤波和与旋转因子相乘的过程与DSLM相同,由于在求取最佳旋转因子时,PAPR计算区间为[T,3T],因此旋转和计算PAPR时的计算量有所区别,对于低复杂度SLM算法的计算复杂度为:CLD-SLM=8MNUT+2MNUT+M,即CLD-SLM=10MNUT+M;式中:N为子载波个数;M为数据块个数;T为码元宽度/符号周期;K为采样因子/重叠因子;Lh为滤波器冲激响应长度;T0为采样周期,Tc为计算PAPR值所取的区间,m为当前数据块,且m∈[0,M-1];通过分析对比上述结果可知,本发明提出的LD-SLM算法比DSLM算法在复杂度上减少10MNUT次实数运算,CLD-SLM≈0.5CDSLM,计算复杂度降低约50%,本发明提出的一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,由于综合考虑了FBMC-OQAM符号的重叠性,即信号大部分能量集中在第2和第3连续的两个FBMC-OQAM符号周期内,故能够很好的适用于FBMC-OQAM系统,在降低系统的PAPR时,本发明提出的LD-SLM算法的性能与DSLM算法非常接近,且计算复杂度与DSLM算法相比减少10MNUT次实数运算,即计算复杂度降低约50%。
附图说明
图1为FBMC-OQAM信号模型;
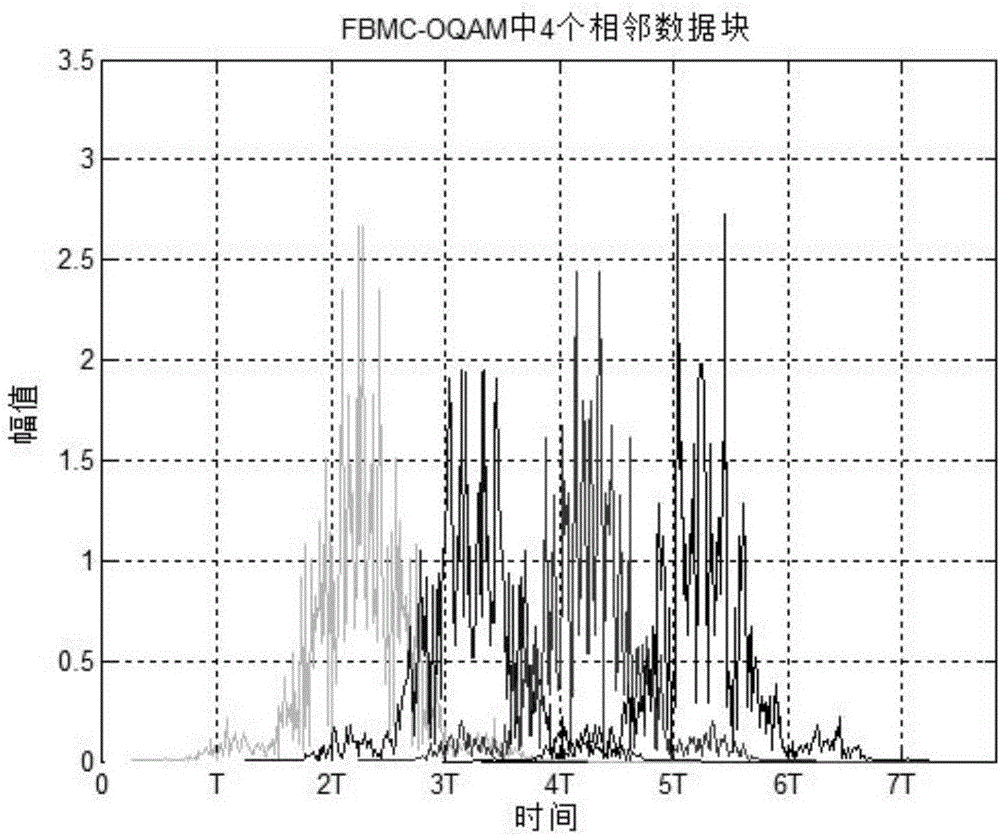
图2为FBMC-OQAM连续4个数据块功率分布;
图3为SLM技术框图;
图4为OFDM-SLM系统不同U值下PAPR;
图5为U=4时不同方案下PAPR分布;
图6为FBMC信号与OFDM信号对比。
具体实施方式
为了进一步说明本发明的技术方案,下面对照附图并结合具体实施例对本发明进行详细的说明。
实施例
本发明提出的一种降低FBMC-OQAM系统PAPR的低复杂度SLM算法,包括以下步骤:
S1、首先初始化旋转矢量,生成U个长度为N的相位旋转矢量:
其中:n∈[0,N-1],u∈[0,U-1];
S2、将当前数据块与旋转矢量相乘,每个输入数据块Xm都与U个不同的旋转矢量相乘:
其中:·表示矩阵点对点乘法;
S3、对信号进行采样、滤波和调制,由于FBMC-OQAM信号的重叠性质,需要考虑当前数据块之前的信号,从而得到如下信号:
其中:m∈[0,2π],t∈[0,(m+1/2)T+4T];
S4、根据下列公式计算信号xu(t)的PAPR,计算区间为Tc;
分析图2仿真结果可知每个信号的功率主要分布在每个信号周期的中间2T区间,故此处Tc∈[mT+T,mT+3T],跨越2T,而DSLM技术中Tc∈[mT,mT+4T],跨越4T;
S5、根据PAPR计算的结果,选择最优旋转方案,得到当PAPR值最小时的旋转矢量编号,即并将umin作为边信息保存在USI=[USI umin]中;
S6、最后更新输入,根据umin选择最佳旋转矢量,与当前数据块相乘,更新输入信号矩阵然后返回步骤S2中,对下一个信号周期的信号Xm+1重复上述步骤,直至m=M-1。
图1所示为FBMC-OQAM信号模型;在FBMC-OQAM系统中,我们采用基于OQAM调制的信号传输,对于含有M个复杂输入信号,N个子载波的发射端可以写成:
其中和分别是第n个子载波上传输的第m个数据块的实部和虚部,信号的实部和虚部在时域上相差T/2(T为符号周期,也称码元宽度),对信号进行过采样,采样周期为T0,过采样因子为K,过采样因子K≥4时,采样后信号的PAPR值与连续信号的PAPR值非常接近,下文仿真中K取4;紧接着信号通过滤波器,通过原型滤波器h(t)和被N个子载波调制之后可以得到:
其中,n=0,1,…,N-1;然后,在N个子载波信号上叠加,可以得到在第m个数据块上的信号:
其中:L为原型滤波器h(t)的长度,可以看出Xm(t)的长度为(L+T/2);最后,将M个数据块叠加在一起可以得到FBMC-OQAM最终信号X(t):
由(2)和(4)可得:
其中,n=0,1,…,N-1;m=0,1,…,M-1,h(t)为原型滤波器的脉冲响应,本文采用PHYDYAS原型滤波器,运用频谱抽样技术,滤波器的长度为L=kN-1,k为重叠因子,N为子载波数数量,其中:
滤波器的脉冲响应如下:
其中,为标准化常量。
图2所示为4个相邻数据块的功率分布,从图中可以看出,每个FBMC-OQAM信号持续4.5T,与随后的3个信号均重叠,且从图中可以看出FBMC-OQAM信号的功率主要分布在其信号持续周期的第2至第3个符号周期之间,即集中在[mT,(m+2)T]之间。对于原型滤波器,能量主要位于主瓣,其长度影响着FBMC-OQAM信号脉冲响应的持续时间,我们定义FBMC-OQAM信号的功率分布如下:
Pavg[X(t)]=|X(t)|2
图3所示为传统的用于减小OFDM系统PAPR的SLM技术的框图。将输入数据X与具有U个不同相位的序列相乘,得到一个修正的数据块Xu,其中n=0,1,…,N-1,u=1,…,U。对U个独立的序列{Xu[n]}取IFFT得到序列xu=[xu[0],xu[1],…,xu[N-1]]T,选择其中具有最小PAPR的序列发射:
图4所示为OFDM-SLM系统不同U值下PAPR,为了使接收机能够恢复原始数据块,需要将作为边信息(Side Information,SI)保存在USI矩阵中,我们选取105个FBMC符号,64个子载波,16个数据块作为仿真参数,仿真OFDM信号运用SLM技术,取不同U值时的PAPR性能,图中曲线从右到左分别是Original,U=4,U=8,U=16,U=32时PAPR的CCDF曲线,分析仿真结果可知,相比原始OFDM系统,运用SLM技术后,其PAPR值有效降低,且随着U值的增大,性能对比也有所提升。
图5所示为U=4时不同方案下PAPR分布,选取105个FBMC符号进行仿真,参数选择为:周期T=64,子载波数N=64,采用4-QAM调制,向量旋转矢量范围为,过采样因子K为4,采样周期T0取4T,选择原型滤波器,跨度为4T。由前面的分析可知,FBMC-OQAM信号的能量主要集中在第2和第3符号周期,故仿真时我们选取的仿真区间为[T,3T],在这个区间计算PAPR的值比之前计算[0,4T]范围内的PAPR值的计算次数大大降低。图5为原始FBMC-OQAM信号PAPR性能与运用DSLM以及运用LD-SLM的FBMC-OQAM在N=64时的PAPR性能对比情况。由图5中仿真结果可以看出,采用LD-SLM算法后,FBMC-OQAM信号的PAPR性能与原始FBMC信号相比有3.5dB的提升;与采用DSLM技术相近,相差只有约0.5dB性能。这说明本文提出的LD-SLM技术在降低FBMC-OQAM系统的PAPR性能上与DSLM相近,但相较原始信号有明显提升。
图6所示为FBMC信号与OFDM信号对比图。我们将运用LD-SLM技术的FBMC-OQAM信号的PAPR与运用传统SLM技术的OFDM信号的PAPR性能作对比。从图6中可以看出,采用LD-SLM算法的FBMC-OQAM信号的PAPR性能与SLM算法PAPR性能很接近,这意味着本文提出的LD-SLM减小PAPR的方案能合理利用FBMC-OQAM信号的重叠性质,且能显著减小信号的PAPR。从图6也可以看出,备选信号数增加时,系统PAPR性能进一步提高。
以上所述,仅为本发明较佳的具体实施方式,但本发明的保护范围并不局限于此,任何熟悉本技术领域的技术人员在本发明揭露的技术范围内,根据本发明的技术方案及其发明构思加以等同替换或改变,都应涵盖在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!