基于校验矩阵的编解码方法和装置与流程
本发明涉及通信技术领域,特别是涉及基于校验矩阵的编码方法和装置以及基于校验矩阵的解码方法和装置。
背景技术:
在数据通过通信链路传输的过程中,由于存在例如噪声的干扰因素,接收端接收到的数据存在一些错误的信息。为了实现数据的可靠传输,可以采用前向纠错(Forward Error Correction,简称FEC)技术,以使得接收端能够识别出接收到的错误信息。作为FEC技术的一种具体实现方式,低密度奇偶校验码(Low Density Parity Check Code,简称LDPC Code或LDPC码)不但具有良好的理论性能而且也适于硬件实现。具体地,LDPC码的理论性能是,LDPC不仅几乎适用于所有的信道而且还能够接近于香农限。LDPC码适于硬件实现的原因在于,LDPC码不仅译码复杂度低,而且可并行实现。基于此,LDPC码已被广泛应用于多种通信协议中,如卫星数字视频广播DVB-S.2、宽带无线接入协议IEEE802.16e以及以太网规范10GBASE-T。
基于LDPC码实现的数据传输具体包括如下步骤:当需要传输数据时,先采用预先构造的LDPC校验矩阵对数据进行编码从而得到编码数据。然后,通过实际链路对编码数据进行传输。接收端接收到编码数据后,采用预先构造的LDPC校验矩阵对编码数据进行解码从而得到所述数据。
在现有技术中,已经出现了一些能够用于编码和解码的LDPC校验矩阵。例如,一种现有的LDPC校验矩阵H如下所示:
其中,LDPC校验矩阵H由J个子矩阵H1、H2、……、Hj组成。LDPC校验矩阵H是m×n维矩阵。子矩阵H1~Hj均是(m/J)×n维矩阵。在矩阵H 中,每行中元素“1”的数量为L,每列中元素“1”的数量为J。在子矩阵H1中,每行中元素“1”的数量为L,每列中元素“1”的数量为J,每行中的L元素“1”是连续的。子矩阵H2~Hj是分别对子矩阵H1进行列置换得到的。
需要说明的是,以LDPC校验矩阵各行表示的校验方程作为校验节点,以LDPC校验矩阵各列表示的变量作为变量节点,可以形成LDPC校验矩阵的泰纳图(Tanner Graph,简称TG),该TG的围长(girth)表示该TG最短环的长度。发明人经过研究发现,现有技术中LDPC校验矩阵对应的TG的围长为4。当围长等于4时,LDPC码性能较低。具体来说,当传输中的LDPC码的信噪比较低时,对接收到的LDPC码进行解码得到的数据的误码率较高。
技术实现要素:
本发明实施例提供一种基于校验矩阵的编码或者解码方法,以及相关装置,以解决现有技术中由于难以避免LDPC校验矩阵的TG的围长等于4而导致的LDPC码性能较低的技术问题。
第一方面,本发明实施例提供了一种基于校验矩阵的编码方法,包括:
编码器获取数据;以及
所述编码器通过利用LDPC校验矩阵对所述数据进行编码,生成编码数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的 数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的 数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
在第一方面的第一种可能的实现方式中,所述LDPC校验矩阵为矩阵H。
在第一方面的第二种可能的实现方式中,所述LDPC校验矩阵是对矩阵H进行行置换和/或列置换而得到的。
第二方面,本发明实施例提供了一种基于校验矩阵的解码方法,包括:
解码器获取编码数据;以及
所述解码器通过利用LDPC校验矩阵对所述编码数据进行解码,生成数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1” 的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
在第二方面的第一种可能的实现方式中,所述LDPC校验矩阵为所述矩阵H。
在第二方面的第二种可能的实现方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或随机列置换而得到的。
第三方面,本发明实施例提供了一种基于校验矩阵的装置,包括:
获取单元,用于获取数据;
生成单元,用于通过利用LDPC校验矩阵对所述第一获取单元获取到的所述数据进行编码,生成编码数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对 角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r) 维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
在第三方面的第一种可能的实现方式中,所述LDPC校验矩阵为所述矩阵H。
在第三方面的第二种可能的实现方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或列置换而得到的。
第四方面,本发明实施例提供了一种基于校验矩阵的装置,包括:
获取单元,用于获取编码数据;
生成单元,用于通过利用LDPC校验矩阵对所述获取模块获取到的所述编码数据进行解码,生成数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3;矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
在第四方面的第一种可能的实现方式中,所述LDPC校验矩阵为所述矩阵H。
在第四方面的第二种可能的实现方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或列置换而得到的。
与现有技术相比,本发明实施例至少具有以下优点:
采用本发明实施例的技术方案,LDPC校验矩阵是基于m×n维的矩阵H而生成的,矩阵H是由三个(m/3)×n维的子矩阵组成,在这三个子矩阵中,每行中元素“1”的数量为L,每列中元素“1”的数量为1,并且,以A表示矩阵中任意两个同一行上的元素“1”之间间隔的元素数量,这三个子矩阵对应A的取值范围是各不相同的,因此,矩阵H中任意两行与任意两列的四个交汇的元素处均至少存在一个“0”,可见,矩阵H对应的TG的围长大于4,这就可以保证LDPC校验矩阵对应的TG的围长大于4,因此,采用这样的LDPC校验矩阵对数据进行编码和解码,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的的误比特率较低,因此,LDPC码的性能得以提高。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本申请中记载的一些实施例,对于本领域普通技术人员来讲,还可以根据这些附图获得其他的附图。
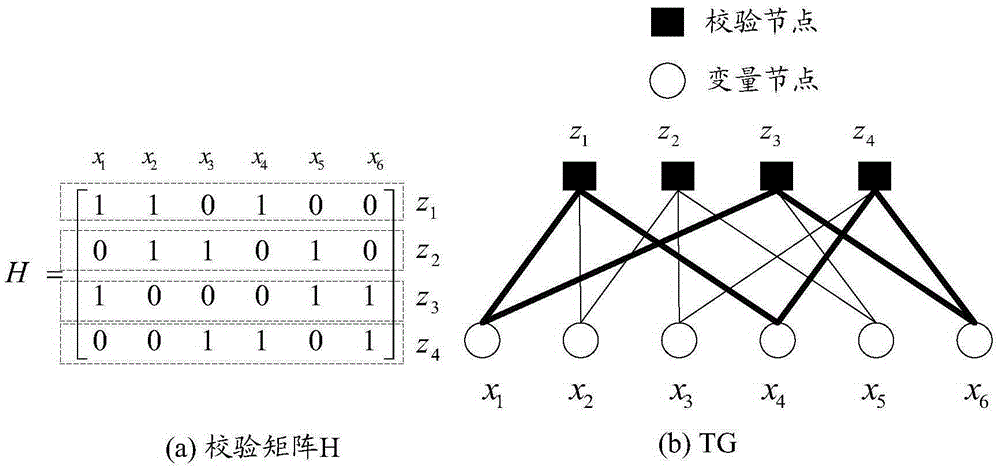
图1为本发明实施例中一种LDPC校验矩阵H与TG之间对应关系的示意图;
图2为本发明实施例中一种对应最小围长的LDPC校验H与TG的示意图;
图3为本发明实施例提供的一应用场景所涉及的系统框架示意图;
图4为本发明实施例中一种基于校验矩阵的编码方法的流程示意图;
图5为本发明实施例中一种矩阵H示例中元素排布的示意图;
图6为本发明实施例中一种矩阵H示例的构造示意图;
图7a为本发明实施例中构造一种矩阵H涉及到的矩阵示意图;
图7b为本发明实施例中构造一种矩阵H涉及到的矩阵示意图;
图8为本发明实施例中一种基于校验矩阵的解码方法的流程示意图;
图9为本发明实施例中一种基于校验矩阵的装置的结构示意图;
图10为本发明实施例中一种基于校验矩阵的装置的结构示意图;
图11为本发明实施例中一种编码器的结构示意图;
图12为本发明实施例中一种解码器的结构示意图。
具体实施方式
为了使本技术领域的人员更好地理解本发明中的方案,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚地描述。显然,所描述的实施例仅是本发明一部分实施例,而不是全部的实施例。
需要说明的是,本申请提及的术语“交汇处”,是指同时位于矩阵中相交的某行和某列的元素的位置。每个交汇处由矩阵中的一个元素占据。可以理解,矩阵中的一行与一列构成一个交汇处。矩阵中的两行与两列构成4个交汇处。此外,本申请中,对于一个矩阵一行来说,该行上任意两个元素“1”之间的元素个数的取值范围,称之为该行的取值范围。如果一个矩阵的每一行中任意两个元素“1”之间的元素个数具有相同的取值范围,则该取值范围即称之为该矩阵的取值范围。例如,对于一个3行的矩阵来说,第1行中任意两个元素“1”之间至少具有a个元素且至多具有b个元素,第2行中任意两个元素“1”之间至少具有a个元素且至多具有b个元素,第3行中任意两个元素“1”之间至少具有a个元素且至多具有b个元素,则第1、2、3行的取值范围均为[a,b],则该矩阵的取值范围为[a,b]。
发明人经过研究发现,在现有技术中,组成LDPC校验矩阵的多个子矩阵是由同一子矩阵经过随机列置换而形成的,导致LDPC校验矩阵对应的TG的围长等于4。而LDPC码的性能高低与LDPC校验矩阵对应的TG的围长有关,当LDPC校验矩阵对应的TG的围长等于4时,LDPC码的性能较低,也即,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的误比特率就会比较高。
图1所示的是LDPC校验矩阵H与TG之间的对应关系。图1包括(a)校验矩阵H以及(b)TG。图1所示的LDPC校验矩阵H与图1所示的TG是相 对应的。其中,该TG包括变量节点x1~x6和校验节点z1~z4。可见,矩阵H的每一列分别对应TG上的一个变量节点,矩阵H的每一行分别对应TG的一个校验节点。对于任意一个变量节点xi与任意一个校验节点zj来说,如果矩阵H中xi所在列与zj所在行交汇处的元素为“1”,则TG上xi与zj是相连的(参见图1中的(b)TG中的粗线)。如果矩阵H中xi所在列与zj所在行交汇处的元素为“0”,则TG上xi与zj是不相连的(参见图1中的(b)TG中的细线)。
可以理解的是,如果要在TG上形成一个环,那么这个环至少要包括两个变量节点和两个校验节点,也就是说,TG理论上的最小围长为4。图2所示的是对应最小围长的LDPC校验矩阵H与TG。图2包括(a)girth为4的校验矩阵H和(b)girth 4的校验矩阵所对应的TG。图2所示的LDPC校验矩阵H与图2所示的TG是相对应的。在该矩阵H上,变量节点x1、x2所在的两行与校验节点z1、z2所在的两列形成了四个交汇处,这四个交汇处的元素均为“1”。因此,在该TG上就形成了由两个变量节点和两个校验节点构成的最短环。因此,该TG的围长为4。由此可见,如果矩阵H上包含满足如下第一约束条件的两行与两列,则该矩阵H对应的TG围长即为4。所述第一约束条件为所述两行与所述两列的四个交汇处的元素都为“1”。如果矩阵H上每两行与每两列均满足如下第二约束条件,则该矩阵H对应的TG围长就大于4。所述第二约束条件为每两行与每两列的四个交汇处的元素均至少存在一个“0”。
在现有技术中,LDPC校验矩阵H由多个子矩阵H1~HJ构成。在每个子矩阵的内部,每一列都只有一个元素“1”。因此,对于任一子矩阵内部的任意两行来说,这两行与任意两列的四个交汇处的元素至少存在两个“0”。但是,矩阵H2~HJ都是由子矩阵H1通过随机列置换得到的,在这种构造下,对于矩阵H中来自两个不同子矩阵的两行来说,无法保证这两行与矩阵H的任意两列的四个交汇处的元素必然存在至少一个“0”,因此,现有技术无法保证LDPC校验矩阵对应的TG的围长大于4,从而导致了LDPC码的性能低。
在本发明实施例中,为了提升LDPC码的性能,提供了一种基于校验矩阵的编解码方法和装置。其中,在用于编解码的LDPC校验矩阵中,任意两行与任意两列的四个交汇处的元素均至少存在一个“0”,从而保证LDPC校验矩阵对应的TG的围长大于4。
图3为本发明实施例提供的技术方案的一种应用场景所涉及的系统框架示意图。参见图3,本发明实施例提供的技术方案可以应用到由编码器301与解码器302组成的系统中。在该系统中,编码器301与解码器302可以采用相同的LDPC校验矩阵实现数据编码和数据解码。具体地,编码器301对于获取到的数据,可以通过利用LDPC校验矩阵对该数据进行编码,生成编码数据。解码器302在获取到该编码数据时,可以通过利用所述LDPC校验矩阵对该数据进行编码,生成该数据。
需要注意的是,上述应用场景仅是为了便于理解本发明的原理而示出,不用于限定本发明实施例提供的技术方案。
下面结合附图,通过实施例来详细说明本发明中基于校验矩阵的编解码和设备的实现方式。
图4为本发明实施例中一种基于校验矩阵的编码方法的流程示意图。在本实施例中,所述方法可以包括如下步骤:
步骤401、编码器获取数据。
步骤402、所述编码器通过利用LDPC校验矩阵对所述数据进行编码,生成编码数据。
具体实现时,所述数据可以是比特串。所述编码数据可以是编码比特串。编码器在获取到所述比特串时,可以利用LDPC校验矩阵对该比特串进行编码,从而生成编码比特串。该编码比特串可以用于在数据链路中传输。例如,所述数据链路可以是光缆、电缆等物理链路,也可以是标签交换路径(Label Switching Path,简称LSP)、伪线(Pseudo Wire,简称PW)等逻辑链路。
在本实施例中,用于编码的LDPC校验矩阵是基于矩阵H生成的。矩阵H是一个m×n维的矩阵。在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3。可见,矩阵H中元素“1”的总数量可以表示为m×L,也可以表示为3×n,因此,m×L=3×n,也即,n=m/3×L。其中,m、n可以由LDPC校验矩阵的实际应用场景来确定。其中,n的取值取决于实际链路中的数据帧长,m的取值取决于编码数据的净荷长度例如,若实际链路的数据帧长为5000并且数据帧长中要求至少要传输3000bit的有用数据,n的取值为 5000,m的取值为5000-3000,即2000。
为了便于构造对应TG的围长大于4的矩阵H,可以将矩阵H划分成三个子矩阵,这三个子矩阵分别构成矩阵H的第1行至第m/3行、第m/3+1行至第2m/3行、第2m/3+1行至第m行。在每个子矩阵中,每行中元素“1”的数量为L,每列中元素“1”的数量为1。在这种情况下,在每个子矩阵内部,任意两行与任意两列的四个交汇处的元素均至少存在两个“0”,因此,在构造每个子矩阵时,仅需要考虑矩阵H中来自两个不同子矩阵的两行与矩阵中任意两列的四个交汇处的元素是否必然存在“0”。
在矩阵H的每一个子矩阵中,各行的取值范围可以是相同的,因此,对于任意一个子矩阵来说,该子矩阵上各行的取值范围即是该子矩阵的取值范围,而任意两个子矩阵的取值范围可以是没有交集的,此时,矩阵H中位于两个不同子矩阵的任意两行与矩阵H中任意两列的四个交汇的元素处必然存在“0”。举例来说,图5为一种矩阵H示例的结构示意图。该矩阵H的行数不小于2,列数不小于13。图5示出了矩阵H的第i行和第j行,以及第z-6列至第z+6列。具体地说,假设两个不同的子矩阵分别对应取值范围[0,2]和[3,4],分别来自这两个子矩阵的i行、j行与z列的两个交汇处的元素均为“1”,在i行上的其余元素“1”仅可能出现在第z-3列至第z-1列或第z+1列至第z+3列,在j行上的其余元素“1”仅可能出现在第z-4列至第z-5列或第z+4列至第z+5列,也即,i行、j行仅与z列的两个交汇处的元素都为“1”,与其他列的两个交汇处的元素都至少存在一个“0”。可见,当各个子矩阵的取值范围各不相同时,对于矩阵H的任意两行来说,如果这两行分别位于两个不同的子矩阵,则这两行与矩阵H的任意两列的四个交汇处的元素中就必然存在“0”。
需要说明的是,为了使得任意两个子矩阵对应的取值范围没有交集,可以根据m/3是否能被L整除,采用不同的方式来构造矩阵H的各子矩阵。当m/3能够被L整除时,采用下述第一种情况介绍的矩阵H,当m/3不能够被L整除时,采用下述第二种情况介绍的矩阵H,也即,本实施例可以采用下述第一情况的矩阵H,或者,也可以采用下述第二种情况的矩阵H。
第一种情况:m/3=k×L且k为正整数,即m/3能够被L整除。
在第一种情况下,矩阵H可以表示为:
具体地,矩阵H可以由矩阵H1、矩阵H2和矩阵H3组成,也即,矩阵H1、矩阵H2和矩阵H3是矩阵H的三个子矩阵。矩阵H1可以构成矩阵H的第1行至第m/3行,矩阵H2可以构成矩阵H的第m/3+1行至第2m/3行,矩阵H3可以构成矩阵H的第2m/3+1行至第m行。可见,矩阵H1、矩阵H2和矩阵H3均为(m/3)×n维。考虑到第一种情况下m/3=k×L,因此,矩阵H1、矩阵H2和矩阵H3的维数也均可以表示成(k×L)×(k×L2)维。
对于(k×L)×(k×L2)维的矩阵H1,矩阵H1的总列数是能够被L整除的,因此,矩阵H1可以按照如下方式来构造:
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。例如,在矩阵H1第1行中,位于第1至L列的元素为“1”,其余元素为“0”。又如,在矩阵H1第2行中,位于第1至L列的元素为“1”,其余元素为“0”。
可见,在矩阵H1的第a1行中,元素“1”均位于第(a1-1)×L+b1列,其中,a1的取值范围为1至k×L中的所有整数,b1的取值范围为1至L中的所有整数。
对于矩阵H1中的任意一行来说,由于该行上所有的L个元素是连续排列在一起的,因此,该行的取值范围的最小值为0,该行的取值范围最大值为L-2。可见,以A1表示矩阵H1中任意一行上任意两个元素“1”之间的元素个数,矩阵H1的取值范围为A1≤L-2。
对于(k×L)×(k×L2)维的矩阵H2,矩阵H2的总列数是能够被总行数整除的,并且,整除的商是L。因此,矩阵H2可以按照如下方式来构造:
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”。
具体地,在矩阵H2中,第1至k×L列构成一个矩阵H4,第k×L+1列至第k×L×2列构成另一个H4,第k×L×2+1列至第k×L×3列构成又一个H4,……,第k×L×(L-1)+1列至第k×L2列构成又一个H4。在任意一个矩阵H4中,位于第1行第1列的元素为“1”,位于第2行第2列的元素为“1”,……,位于第k×L行第k×L列的元素为“1”,其余元素均为“0”。
可见,在矩阵H2的第a2行中,元素“1”均位于第a2+b2×k×L列,其中,a2的取值范围为1至k×L中的所有整数,b2的取值范围为0至L-1中的所有整数。例如,在矩阵H2第1行中,位于第1、k×L+1、k×L×2+1、……、k×L×(L-1)+1列的元素为“1”。又如,在矩阵H2第2行中,位于第2、k×L+2、k×L×2+2、……、k×L×(L-1)+2列的元素为“1”。
对于矩阵H2中的任意一行来说,该行上每两个相距最近的元素“1”之间均具有有k×L-1个元素“0”,并且,该行上元素“1”的数量为L,可见,该行的取值范围的最小值为k×L-1,该行的取值范围的最大值为k×L×(L-1)-1。可见,以A2表示矩阵H2中任意一行上任意两个元素“1”之间的元素个数,矩阵H2的取值范围为k×L-1≤A2≤k×L×(L-1)-1。
对于(k×L)×(k×L2)维的矩阵H3,矩阵H3的总列数能够被L2整除且整除得到的商为k,矩阵H3的总行数能够被L整除且整除得到的商也为k。因此,矩阵H3可以按照如下方式来构造:
在矩阵H3中,每行中元素“1”的数量等于L,每列中元素“1”的数量 等于1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”。在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数。
具体地,在矩阵H3中,第1行至第L行与第1列至第L2列构成第1个矩阵H5,即对应于i取1,第L+1行至第2×L行至第L2+1列至第2×L2列构成第2个矩阵H5,即对应于i取2,……,第(k-1)×L+1行至k×L行与第(k-1)×L2+1列至第k×L2列构成第i个矩阵H5,即对应于i取k。在任意一个矩阵H5中,第1列至第L列构成一个矩阵H6,第L+1列至第2×L列构成另一个矩阵H6,……,第(L-1)×L列至第L2列构成又一个矩阵H6。在任意一个矩阵H6中,位于第1行第1列的元素为“1”,位于第2行第2列的元素为“1”,……,位于第L行第L列的元素为“1”,其余元素均为0。
可见,在矩阵H3的第a3+b3×L行中,元素“1”均位于第a3+b3×L2+c3×L列,其中,a3的取值范围为1至L中的所有整数,b3的取值范围为0至k-1中的所有整数,c3的取值范围为0至L-1范围内的所有整数。例如,矩阵H3第1行对应a3取1且b3取0,在矩阵H3第1行中,位于第1、L+1、……、L×(L-1)+1列的元素为“1”。又如,矩阵H3第2行对应a3取2且b3取0,在矩阵H3第2行中,位于第2、L+2、……、L×(L-1)+2列的元素为“1”。再如,矩阵H3第L+1行对应a3取1且b3取1,在矩阵H3第L+1行中,位于第L2+1、L2+L+1、……、L2+L×(L-1)+1列的元素为“1”。
对于矩阵H3中的任意一行来说,该行上每两个相距最近的元素“1”之间均间隔有L-1个元素“0”,并且,该行上元素“1”的数量为L,可见,该行的取值范围的最小值为L-1,该行的取值范围的最大值为L×(L-1)-1。可见,以A3表示矩阵H3中任意一行上任意两个元素“1”之间的元素个数,矩阵H3的取值范围为L-1≤A3≤L×(L-1)-1。
作为一种示例,根据前述矩阵H1、矩阵H2和矩阵H3的构造方式,当k=3且L=2时,矩阵H可以构造成如图6所示的形式。
需要说明的是,对于本实施例第一种情况的矩阵H,在k大于L的情况 下,上述A1、A2、A3的取值范围是互不相同的,因此,该矩阵H中任意两行与任意两列的四个交汇处的元素均至少存在一个“0”,因此,该矩阵H对应TG的围长不为4。
具体地,以i行和j行表示矩阵H的任意两行。i行与j行可以位于矩阵H的同一子矩阵,即,i行与j行可以均位于矩阵H1、矩阵H2和矩阵H3中的任意一个矩阵。i行与j行也可以位于矩阵H的两个不同的子矩阵,即,i行与j行可以分别位于矩阵H1、矩阵H2和矩阵H3中的任意两个矩阵。
在i行与j行位于同一子矩阵的情况下,由于矩阵H1、矩阵H2和矩阵H3的每列中均有且只有一个元素“1”,因此,i行、j行与矩阵H中任意一列的两个交汇处的元素都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H1,j行可以位于矩阵H2。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处的元素均为“1”,根据矩阵H1的取值范围和矩阵H2的取值范围,除了z列上的元素“1”之外,i行上的其他元素“1”仅可能位于第z-L+1列至第z+L-1列,j行上的其他元素“1”仅可能位于第z-k×L×(L-1)列至第z-k×L列及第z+k×L列至第z+k×L×(L-1)列,可见,在k为正整数的情况下,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j行与任意两列的四个交汇处的元素中都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H1,j行可以位于矩阵H3。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处的元素均为“1”,根据矩阵H1的取值范围和矩阵H3的取值范围,除了z列上的元素“1”之外,i行上的其他元素“1”仅可能位于第z-L+1列至第z+L-1列,j行上的其他元素“1”仅可能位于第z-L×(L-1)列至第z-L列及第z+L列至第z+L×(L-1)列,可见,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j行与任意两列的四个交汇处的元素中都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H2,j行可以位于矩阵H3。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处的元素均为“1”,根据矩阵H2的取值范围和矩阵H3的取值范围,除了z列上的 元素“1”之外,i行上的其他元素“1”仅可能位于第z-k×L×(L-1)列至第z-k×L列及第z+k×L列至第z+k×L×(L-1)列,j行上的其他元素“1”仅可能位于第z-L×(L-1)列至第z-L列及第z+L列至第z+L×(L-1)列,可见,在k大于L的情况下,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j行与任意两列的四个交汇处的元素中都至少存在一个“0”。
通过上述分析可知,对于矩阵H中的任意两行,无论这两行是均位于矩阵H1、矩阵H2和矩阵H3中的任意一个矩阵,还是分别位于矩阵H1、矩阵H2和矩阵H3中的任意两个矩阵,这两行与矩阵H中任意两列的四个交汇处的元素都至少存在一个“0”,因此,矩阵H对应的TG的围长大于4。
第二种情况:m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,即m/3不能够被L整除。
在第二种情况下,矩阵H可以表示为:
具体地,矩阵H可以由矩阵H1’、矩阵H2’和矩阵H3’组成,也即,矩阵H1’、矩阵H2’和矩阵H3’是矩阵H的三个子矩阵。矩阵H1’可以构成矩阵H的第1行至第m/3行,矩阵H2’可以构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’可以构成矩阵H的第2m/3+1行至第m行。可见,矩阵H1’、矩阵H2’和矩阵H3’均为(m/3)×n维。考虑到第一种情况下m/3=k×L+r,因此,矩阵H1’、矩阵H2’和矩阵H3’的维数也可以表示成(k×L+r)×(k×L2+r×L)维的矩阵。
对于(k×L+r)×(k×L2+r×L)维的矩阵H1’,矩阵H1’的总列数是能够被L整除的。因此,矩阵H1’可以按照如下方式来构造:
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量 等于1,每行中的L个元素“1”是连续的。例如,在矩阵H1’第1行中,位于第1至L列的元素为“1”,其余元素为“0”。又如,在矩阵H1’第2行中,位于第1至L列的元素为“1”,其余元素为“0”。
可见,在矩阵H1’的第a1’行中,元素“1”均位于第(a1’-1)×L+b1’列,其中,a1’的取值范围为1至k×L+r中的所有整数,b1’的取值范围为1至L中的所有整数。
可以理解的是,由于矩阵H1’与前述矩阵H1在每行上对元素“1”采用了相似的排列方式,参考前述矩阵H1可知,以A1’表示矩阵H1’中任意一行上任意两个元素“1”之间的元素个数,矩阵H1’的取值范围为A1’≤L-2。
对于(k×L+r)×(k×L2+r×L)维的矩阵H2’,矩阵H2’的总列数是能够被总行数整除的,并且,整除得的商是L。因此,矩阵H2可以按照如下方式来构造:
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”。
具体地,在矩阵H2’中,第1至k×L+r列构成一个矩阵H4’,第k×L+r+1列至第k×L×2+r×2列构成另一个H4’,……,第k×L×(L-1)+r×(L-1)+1列至第k×L2+r×L列构成又一个H4’。在任意一个矩阵H4’中,元素“1”位于第1行第1列、第2行第2列、……、第k×L+r行第k×L+r列的位置。
可见,在矩阵H2’的第a2’行中,元素“1”均位于第a2’+b2’×(k×L+r)列,其中,a2的取值范围为1至k×L+r中的所有整数,b2’的取值范围为0至L-1中的所有整数。例如,在矩阵H2’第1行中,元素“1”位于第1、k×L+r+1、k×L×2+r×2+1、……、k×L×(L-1)+r×(L-1)+1列。又如,在矩阵H2’第2行中,元素“1”位于第2、k×L+r+2、k×L×2+r×2+2、……、k×L×(L-1)+r×(L-1)+2列。
可以理解的是,由于矩阵H2’与前述矩阵H2在每行上对元素“1”采用了相似的排列方式,参考前述矩阵H2可知,以A2’表示矩阵H2’中任意一行上任 意两个元素“1”之间的元素个数,矩阵H2’的取值范围为k×L+r-1≤A2’≤(k×L+r)×(L-1)-1。
对于(k×L+r)×(k×L2+r×L)维的矩阵H3’,矩阵H3’的总列数不能够被L2整除,矩阵H3’的总列数除以L2,商为k,余数为r×L,并且,矩阵H3的总行数不能够被L整除,矩阵H3’的总行数除以L,商为k,余数为r。因此,可以先构造一个(k×L+r)×(k×L2+r×L)维的矩阵H5’,再对矩阵H5’进行列置换可以得到矩阵H3’。其中,矩阵H5’可以按照如下方式来构造:
在矩阵H5’中,第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”。矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H6’等于矩阵H3。矩阵H7’为r×(r×L)维的矩阵,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
具体地,矩阵H6’与前述矩阵H3均是(k×L)×(k×L2)维的矩阵,因此可以采用矩阵H3作为矩阵H6’。参照矩阵H3可知,在矩阵H6’中的第a6’+b6’×L行中,元素“1”均位于第a6’+b6’×L2+c6’×L列,其中,a6’的取值范围为1至L中的所有整数,b6’的取值范围为0至k-1中的所有整数,c6’的取值范围为0至L-1范围内的所有整数。
矩阵H7’与前述矩阵H1具有相似的特点,两者均是总列数除以总行数的商为L,因此参照矩阵H1,可以将矩阵H7’每行上的元素“1”连续排列在一起,即,在矩阵H7’中的第a7’行,元素“1”均位于第(a7’-1)×L+b7’列,其中,a7’的取值范围为1至r中的所有整数,b7’的取值范围为1至L中的所有整数。
由矩阵H6’和矩阵H7’可知,在矩阵H5’第1行至第k×L行中的第a5’+b5’×L行中,元素“1”均位于第a5’+b5’×L2+c5’×L列,在矩阵H5’第k×L+1行至第k×L+r行中的第d5’+k×L行中,元素“1”均位于第(d5’-1)×L+e5’+k×L2列,其中,a5’- 的取值范围为1至L中的所有整数,b5’的取值范围为0至k-1中的所有整数,c5’的取值范围为0至L-1范围内的所有整数,d5’的取值范围为1至r中的所有整数,e5’的取值范围为1至L中的所有整数。例如,矩阵H5’第1行对应a5’取1且b5’取0,在矩阵H5’第1行中,元素“1”位于第1、L+1、……、L×(L-1)+1列。又如,矩阵H5’第k×L行对应a5’取L且b5’取k-1,在矩阵H5’第k×L行中,元素“1”位于第L、L×2、……、L×L列。又如,矩阵H5’第k×L+1行对应d5’取1,在矩阵H5’第k×L+1行中,元素“1”位于第k×L2+1至k×L2+L列的元素。又如,矩阵H5’第k×L+r行对应d5’取r,在矩阵H5’第k×L+r行中,元素“1”位于第k×L2+(r-1)×L+1至k×L2+r×L列。
在矩阵H5’构造完成之后,将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换,可以得到矩阵H3’,其中,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数。例如,对应b取0且c取1,需要将矩阵H5’中第k×L2+1列与第1列进行位置互换。又如,对应b取1且c取2,需要将矩阵H5’中第k×L2+L+2列与第L2+L+2列进行位置互换。又如,对应b取r-1且c取L,需要将矩阵H5’中第k×L2+r×L列与第r×L2列进行位置互换。
可以理解的是,按照上述方式构造的矩阵H3’,可以表示为:
具体地,矩阵H3’包括矩阵H8’、矩阵H9’、矩阵H10’和矩阵H11’。矩阵H3’中第1行至第r×L行与第1列至第r×L2列对应的矩阵等于矩阵H8’,矩阵H3’中第r×L+1行至第k×L行与第r×L2+1列至第k×L2列对应的矩阵等于矩阵H9’,矩阵H3’中第1行至第r×L行与第k×L2+1列至第k×L2+r×L列对应的矩阵等于矩阵H10’,矩阵H3’中其余元素为“0”。
矩阵H8’包括r个矩阵H12’,所述r个矩阵H12’中第i个矩阵等于矩阵H8’中第(i-1)×L+1行至第i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至r中的所有整数。所述矩阵H12’是由矩阵H121’、矩阵H122’、……、矩阵H12L’共L个矩阵组成。在矩阵H121’至矩阵H12L’中的任意一个矩阵中,位于主对角线上的L个元素包括L-1个元素“1”和1个元素“0”。在矩阵H121’至矩阵H12L’中的矩阵H12i’中,第i行第i列上的元素为“0”。
矩阵H9’包括k-r个矩阵H13’,所述k-r个矩阵H13’中第i个矩阵等于矩阵H9’中第(i-1)×L+1行至第i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k-r中的所有整数。矩阵H13’等于前述的矩阵H5。
矩阵H10’为(r×L)×(r×L)维的矩阵,矩阵H10’主对角线上的元素为“1”。
矩阵H11’包括r个矩阵H14’,所述r个矩阵H14’中第i个矩阵等于矩阵H11’中第i行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至r中的所有整数。矩阵H14’包括L个元素“1”。在矩阵H14’中,每两个相距最近的元素“1”之间间隔有L-1个元素“0”。
由上述构造的矩阵H3’可知,在矩阵H3’第1行至第r×L行中的第a3’+b3’×L行中,元素“1”均位于第a3’+d3’×L2+c3’×L列及第a3+b3’×L+k×L2列,在矩阵H3’第r×L+1行至第k×L行中的第a3’+b3’×L行中,元素“1”均位于第a3’+b3’×L2+c3’×L列,在矩阵H5’第k×L+1行至第k×L+r行中的第e3’+k×L行中,元素“1”均位于第(e3’-1)×L 2+(f5’-1)×L+f5’列,其中,a3’的取值范围为1至L中的所有整数,b3’的取值范围为0至k-1中的所有整数,c3’的取值范围为0至L-1范围内的所有整数,d3’=b3’且d3’≠a3’-1,e3’的取值范围为1至r中的所有整数,f3’的取值范围为1至L中的所有整数。
在矩阵H3’第1行至第r×L行中的任意一行上,前k×L2列共有L-1个“1”元素,其中,两个元素“1”之间至少具有L-1个元素,两个元素“1”之间至多具有L×(L-1)-1个元素。在该行上,位于后r×L列的元素中仅有1个“1”,该元素“1”与位于前k×L2列的元素“1”之间至少具有k×L2-r×L2+r×L-1。在矩阵H3’第r×L+1行至第k×L行中的任意一行上,两个元素“1”之间至少具有L-1个元素,两个元素“1”之间至多具有L×(L-1)-1个元素。在矩阵H3’第k×L+1行至第k×L+r行中的任意一行上,两个元素“1”之间至少具有L个元素,两个元素“1”之间至多具有L2个元素。由此可见,以A3’表示矩阵H3’中任意一行上任意两个元素“1”之间的元素个数,矩阵H3’的取值范围为L-1≤A3’≤L2-1或A3’≥k×L2-r×L2+r×L-1。
作为一种示例,根据前述矩阵H1’、矩阵H2’和矩阵H3’的构造方式,当k=3、L=2且r=1时,矩阵H可以构造成如图7a和图7b所示的形式。其中,图7a示出的是构造矩阵H1’的方式、构造矩阵H2’的方式以及构造矩阵H5’的方式,图7b示出的是矩阵H5’经过列置换构造矩阵H3’的方式以及矩阵H1’、矩阵H2’和矩阵H3’构造矩阵H的方式。
需要说明的是,对于本实施例第二种情况的矩阵H,在k大于L2-L的情况下,上述矩阵H1’、矩阵H2’、矩阵H3’的取值范围是互不相同的,因此,该矩阵H中任意两行与任意两列的四个交汇处的元素均至少存在一个“0”,因此,该矩阵H对应TG的围长大于4。
具体地,以i行和j行表示矩阵H的任意两行。i行与j行可以位于矩阵H的同一子矩阵,即,i行与j行可以均位于矩阵H1’、矩阵H2’和矩阵H3’中 的任意一个矩阵。i行与j行也可以位于矩阵H的两个不同的子矩阵,即,i行与j行可以分别位于矩阵H1’、矩阵H2’和矩阵H3’中的任意两个矩阵。
在i行与j行位于同一子矩阵的情况下,由于矩阵H1’、矩阵H2’和矩阵H3’的每列中均有且只有一个元素“1”,因此,i行、j行与矩阵H中任意一列的两个交汇处的元素都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H1’,j行可以位于矩阵H2’。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处的元素均为“1”,根据矩阵H1’的取值范围和矩阵H2’的取值范围,除了z列上的元素“1”之外,i行上的其他元素“1”仅可能位于第z-L+1列至第z+L-1列,j行上的其他元素“1”仅可能位于第z-(k×L+r)×(L-1)列至第z-k×L-r列及第z+k×L+r列至第z+(k×L+r)×(L-1)列,可见,在k大于L2-L的情况下,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j行与任意两列的四个交汇处的元素中都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H1’,j行可以位于矩阵H3’。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处的元素均为“1”,根据矩阵H1’的取值范围和矩阵H3’的取值范围,除了z列上的元素“1”之外,i行上的其他元素“1”仅可能位于第z-L+1列至第z+L-1列,j行上的其他元素“1”仅可能位于第z-L2列至第z-L列及第z+L列至第z+L2列、第z-k×L2+r×L2-r×L列和第z+k×L2-r×L2+r×L列,可见,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j行与任意两列的四个交汇处的元素中都至少存在一个“0”。
在i行与j行位于不同子矩阵的情况下,i行可以位于矩阵H2’,j行可以位于矩阵H3’。假设矩阵H中存在一个z列使得i行、j行与z列的两个交汇处元素均为“1”,根据矩阵H2’的取值范围和矩阵H3’的取值范围,除了z列上的元素“1”之外,i行上的其他元素“1”仅可能位于第z-(k×L+r)×(L-1)列至第z-k×L-r列及第z+k×L+r列至第z+(k×L+r)×(L-1)列,j行上的其他元素“1”仅可能位于第z-L2列至第z-L列及第z+L列至第z+L2列、第z-k×L2+r×L2-r×L列和第z+k×L2-r×L2+r×L列,可见,在k大于L2-L的情况下,除了z列之外,i行的元素“1”与j行的元素“1”不会同时出现在同一列上,因此,i行、j 行与任意两列的四个交汇处的元素中都至少存在一个“0”。
通过上述分析可知,对于矩阵H中的任意两行,无论这两行是均位于矩阵H1’、矩阵H2’和矩阵H3’中的任意一个矩阵,还是分别位于矩阵H1’、矩阵H2’和矩阵H3’中的任意两个矩阵,这两行与矩阵H中任意两列的四个交汇处的元素都至少存在一个“0”,因此,矩阵H对应的TG围长大于4。
在一些实施方式中,LDPC校验矩阵可以是矩阵H。矩阵H本身对应的TG的围长大于4,即相当于LDPC校验矩阵对应的TG的围长大于4。
在另一些实施方式中,LDPC校验矩阵可以是对矩阵H进行行置换而得到的,即,从矩阵H中选择任意多行进行位置互换,互换后得到LDPC矩阵。例如,选取矩阵H的第1、5、10行,将第1行换到第5行,将第5行换到第10行,将第10行换到第1行,从而得到LDPC校验矩阵。
在又一些实施方式中,LDPC校验矩阵可以是对矩阵H进行列置换而得到的,即,从矩阵H中选择任意多列进行位置互换,互换后得到LDPC校验矩阵。例如,选取矩阵H的第3、6、7列,将第3列换到第7列,将第6行换到第3列,将第7列换到第6列,从而得到LDPC校验矩阵。
在又一些实施方式中,LDPC校验矩阵可以是对矩阵H进行行置换和列置换而得到的,即,从矩阵H中先选择任意多行进行位置互换再选择任意多列进行位置互换,互换后得到LDPC校验矩阵,或者,从矩阵H中先选择任意多列进行位置互换再选择任意多行进行位置互换,互换后得到LDPC校验矩阵。
可以理解的是,无论是矩阵的行置换还是矩阵的列置换,都不会改变矩阵对应的TG的围长。因此,通过矩阵H的行置换和/或列置换得到的LDPC校验矩阵,与矩阵H具有相同的TG的围长,因此,LDPC校验矩阵对应的TG的围长大于4。
需要说明的是,矩阵X中第Y行表示矩阵X从最顶端开始向下的第Y个行向量,矩阵X中第Z列表示矩阵X从最左侧开始向右的第Z个行向量,其中,矩阵X可以是上述提及的任意一个矩阵,第Y行可以是上述提及的任意一个矩阵的任意一行,第Z列可以是上述提及的任意一个矩阵的任意一列。
通过本实施例的技术方案,无论是上述第一种情况还是上述第二种情况, m×n维的矩阵H都是由三个(m/3)×n维的子矩阵组成,在这三个子矩阵中,每行中元素“1”的数量为L,每列中元素“1”的数量为1,并且,这三个子矩阵的取值范围是各不相同的,这使得矩阵H中任意两行与任意两列的四个交汇处的元素均至少存在一个“0”,保证矩阵H对应的TG的围长大于4,因此,基于矩阵H生成LDPC校验矩阵,就可以保证LDPC校验矩阵对应的TG的围长大于4,因此,采用这样的LDPC校验矩阵对数据进行编码,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的的误比特率较低,因此,LDPC码的性能得以提高。
图8为本发明实施例中一种基于校验矩阵的解码方法的流程示意图。在本实施中,所述方法包括如下步骤:
步骤801、解码器获取编码数据。
步骤802、所述解码器通过利用低密度奇偶校验LDPC校验矩阵对所述编码数据进行解码,生成数据。
需要说明的是,图4所示的方法以及图8所示的方法可以应用于图3所示的应用场景。具体地,图4所示的方法的执行主体可以是图3中的编码器301。图8所示的方法的执行主体可以是图3中的解码器302。图8中步骤801涉及的编码数据可以是图4中步骤402涉及的编码数据。图8所示的步骤802中的解码处理是图4所示的步骤402中的编码处理的逆处理。因此,图8所示的步骤802具体实现时,可以参考实施例对图8所示的步骤802的描述。
具体实现时,解码器可以以比特串的形式对数据进行获取和解码。解码器在获取到编码比特串时,可以利用LDPC校验矩阵对该编码比特串进行解码,从而生成比特串。该编码比特串可以用于在实际数据链路中传输。在本实施例中,用于解码的LDPC校验矩阵是基于矩阵H生成的。在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵。其中,本实施例可以采用下述第一种情况的矩阵H,或者,也可以采用下述第二种情况的矩阵H。
第一种情况:m/3=k×L且k为正整数,即m/3能够被L整除。
在第一种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵。
矩阵H1可以按照如下方式来构造:
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2可以按照如下方式来构造:
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”。
矩阵H3可以按照如下方式来构造:
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”。 在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数。
第二种情况:m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,即m/3不能够被L整除。
在第二种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵。
矩阵H1’可以按照如下方式来构造:
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2’可以按照如下方式来构造:
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”。
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位 置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数。
矩阵H5’可以按照如下方式来构造:
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”。
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵。矩阵H6’等于矩阵H3。在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
可选的,在一些实施方式中,所述LDPC校验矩阵为所述矩阵H。
可选的,在另一些实施方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或随机列置换而得到的。
需要说明的是,本实施例中,矩阵H、LDPC校验矩阵可以采用图4所示实施例中提及方式进行构造,具体可参见前述图4所示的实施例的相关内容,本实施例在此不再赘述。
通过本实施例的技术方案,无论是上述第一种情况还是上述第二种情况,m×n维的矩阵H都是由三个(m/3)×n维的子矩阵组成,在这三个子矩阵中,每行中元素“1”的数量为L,每列中元素“1”的数量为1,并且,这三个子矩阵的取值范围是各不相同的,这使得矩阵H中任意两行与任意两列的四个交汇处的元素均至少存在一个“0”,保证矩阵H对应的TG的围长大于4,因此,基于矩阵H生成LDPC校验矩阵,就可以保证LDPC校验矩阵对应的TG的围长大于4,因此,采用这样的LDPC校验矩阵对数据进行解码,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的的误比特率较低,因此,LDPC码的性能得以提高。
图9为本发明实施例中一种基于校验矩阵的装置900的结构示意图。所述装置900具体包括:
获取单元901,用于获取数据;
生成单元902,用于通过利用低密度奇偶校验LDPC校验矩阵对所述获取单元901获取到的所述数据进行编码,生成编码数据。
举例来说,图9所示的基于校验矩阵的设备可以用于执行图4所示的方法。具体地,获取单元901可以用于执行图4中的步骤401。生成单元902可以用于执行图4中的步骤402。
具体实现时,获取单元901可以以比特串的形式对数据进行获取,生成单元902可以以比特串的形式对数据进行编码。在编码器900中,获取单元901获取一个比特串,生成单元902利用LDPC校验矩阵对该比特串进行编码,从而生成一个编码比特串。该编码比特串可以用于在实际数据链路中传输。其中,所述装置900例如可以实现为编码器、处理器芯片等。所述获取单元901例如可以实现为接收器、存储器等获取电路。所述生成单元902例如可以实现为编码电路。
在本实施例中,用于编码的LDPC校验矩阵是基于矩阵H生成的。在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵。其中,本实施例可以采用下述第一种情况的矩阵H,或者,也可以采用下述第二种情况的矩阵H。
第一种情况:m/3=k×L且k为正整数,即m/3能够被L整除。
在第一种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵。
矩阵H1可以按照如下方式来构造:
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2可以按照如下方式来构造:
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”。
矩阵H3可以按照如下方式来构造:
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”。在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数。
第二种情况:m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,即m/3不能够被L整除。
在第二种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵。
矩阵H1’可以按照如下方式来构造:
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2’可以按照如下方式来构造:
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”。
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数。
矩阵H5’可以按照如下方式来构造:
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”。
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵。矩阵H6’等于矩阵H3。在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
可选的,在一些实施方式中,所述LDPC校验矩阵为所述矩阵H。
可选的,在另一些实施方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或随机列置换而得到的。
需要说明的是,本实施例中,矩阵H的构造、LDPC校验矩阵的构造,具体可参见前述图4所示的实施例的相关内容,本实施例在此不再赘述。
通过本实施例的技术方案,可以保证矩阵H对应的TG的围长大于4,因此,基于矩阵H生成LDPC校验矩阵,就可以保证LDPC校验矩阵对应的TG的围长大于4,因此,装置900采用这样的LDPC校验矩阵对数据进行编码,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的的误比特率较低,因此,LDPC码的性能得以提高。
图10为本发明实施例中一种基于校验矩阵的装置1000的结构示意图。所述装置1000包括:
获取单元1001,用于获取编码数据;
生成单元1002,用于通过利用低密度奇偶校验LDPC校验矩阵对所述获取单元1002获取到的所述编码数据进行解码,生成数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3;矩阵H为m×n维的矩阵。
图10所示的基于校验矩阵的设备可以用于执行图8所示的方法。具体地, 获取单元1001可以用于执行图8中的步骤801。生成单元1002可以用于执行图8中的步骤802。
具体实现时,获取单元1001可以以比特串的形式对数据进行获取,生成单元1002可以以比特串的形式对数据进行解码。在解码器1000中,获取单元1001获取一个编码比特串,生成单元1002利用LDPC校验矩阵对该编码比特串进行解码,从而生成一个比特串。该编码比特串可以用于在实际数据链路中传输。其中,所述装置1000例如可以实现为解码器、处理器芯片等。所述获取单元1001例如可以实现为接收器、存储器等获取电路。所述生成单元1002例如可以实现为解码电路。在本实施例中,用于解码的LDPC校验矩阵是基于矩阵H生成的。在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵。其中,本实施例可以采用下述第一种情况的矩阵H,或者,也可以采用下述第二种情况的矩阵H。
第一种情况:m/3=k×L且k为正整数,即m/3能够被L整除。
在第一种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵。
矩阵H1可以按照如下方式来构造:
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2可以按照如下方式来构造:
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”。
矩阵H3可以按照如下方式来构造:
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”。在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数。
第二种情况:m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,即m/3不能够被L整除。
在第二种情况下,矩阵H可以表示为:
具体地,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵。
矩阵H1’可以按照如下方式来构造:
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的。
矩阵H2’可以按照如下方式来构造:
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”。
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数。
矩阵H5’可以按照如下方式来构造:
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”。
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵。矩阵H6’等于矩阵H3。在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
可选的,在一些实施方式中,所述LDPC校验矩阵为所述矩阵H。
可选的,在另一些实施方式中,所述LDPC校验矩阵是对所述矩阵H进行随机行置换和/或随机列置换而得到的。
需要说明的是,本实施例中,矩阵H的构造、LDPC校验矩阵的构造,具体可参见前述图4所示的实施例的相关内容,本实施例在此不再赘述。
通过本实施例的技术方案,可以保证矩阵H对应的TG的围长大于4,因此,基于矩阵H生成LDPC校验矩阵,就可以保证LDPC校验矩阵对应的TG的围长大于4,因此,解码器1000采用这样的LDPC校验矩阵对数据进行解码,当传输中的LDPC码的信噪比比较低时,对接收到的LDPC码进行解码得到的数据的的误比特率较低,因此,LDPC码的性能得以提高。
图11为本发明实施例中一种编码器的结构示意图。在本实施例中,编码器1100包括:处理器1101、存储器1102、网络接口1103、总线系统1104。
所述总线系统1104,用于将编码器设备1100的各个硬件组件耦合在一起。
所述网络接口1103,用于实现编码器设备1100与至少一个其它网元之间的通信连接,可以使用互联网,广域网,本地网,城域网等方式。
所述存储器1102,用于存储程序指令和数据。
所述处理器1101,用于读取存储器1102中存储的指令和数据,执行以下操作:
处理器1101获取数据;以及
处理器1101通过利用低密度奇偶校验矩阵LDPC校验矩阵对所述数据进行编码,生成编码数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
可选的,处理器1101采用的所述LDPC校验矩阵,例如可以为矩阵H。
可选的,处理器1101采用的所述LDPC校验矩阵,例如可以是对矩阵H 进行行置换和/或列置换而得到的。
图11所示的编码器可以用于实现图9所示的基于校验矩阵的装置。另外,图11所示的编码器可以用于执行图4所示的方法。
图12为本发明实施例中一种解码器的结构示意图。在本实施例中,解码器1200包括:处理器1201、存储器1202、网络接口1203、总线系统1204。
所述总线系统1204,用于将解码器设备1200的各个硬件组件耦合在一起。
所述网络接口1203,用于实现解码器设备1200与至少一个其它网元之间的通信连接,可以使用互联网,广域网,本地网,城域网等方式。
所述存储器1202,用于存储程序指令和数据。
所述处理器1201,用于读取存储器1202中存储的指令和数据,执行以下操作:
处理器1201获取编码数据;以及
处理器1201通过利用低密度奇偶校验LDPC校验矩阵对所述编码数据进行解码,生成数据,所述LDPC校验矩阵是基于矩阵H生成的,在矩阵H中,每行中元素“1”的数量为L,每列中元素“1”的数量为3,矩阵H为m×n维的矩阵;
m/3=k×L且k为正整数,矩阵H由矩阵H1、矩阵H2和矩阵H3组成,矩阵H1构成矩阵H的第1行至第m/3行,矩阵H2构成矩阵H的第m/3+1行至第2m/3行,矩阵H3构成矩阵H的第2m/3+1行至第m行,矩阵H1、矩阵H2和矩阵H3均为(k×L)×(k×L2)维的矩阵;
其中,
在矩阵H1中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2由L个矩阵H4组成,矩阵H4为(k×L)×(k×L)维的对角阵,矩阵H4的主对角线上的元素都是“1”;
在矩阵H3中,每行中的元素“1”的数量为L,每列中的元素“1”的数量为1,矩阵H3包括k个矩阵H5,矩阵H5包括L个矩阵H6,矩阵H5为L×L2维的矩阵,矩阵H6为L×L维的对角阵,矩阵H6的主对角线上的元素都是“1”;
在矩阵H3中,所述k个矩阵H5之外的元素均为“0”,所述k个矩阵H5中第i个矩阵等于矩阵H3中第(i-1)×L+1行至i×L行与第(i-1)×L2+1列至第i×L2列对应的矩阵,i的取值范围为1至k中的所有整数;
或者,
m/3=k×L+r且k为正整数、r为1至L-1范围内的正整数,矩阵H由矩阵H1’、矩阵H2’和矩阵H3’组成,矩阵H1’构成矩阵H的第1行至第m/3行,矩阵H2’构成矩阵H的第m/3+1行至第2m/3行,矩阵H3’构成矩阵H的第2m/3+1行至第m行,矩阵H1’、矩阵H2’和矩阵H3’均为(k×L+r)×(k×L2+r×L)维的矩阵;
其中,
在矩阵H1’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,每行中的L个元素“1”是连续的;
在矩阵H2’中,每行中元素“1”的数量等于L,每列中元素“1”的数量等于1,矩阵H2’由L个矩阵H4’组成,矩阵H4’为(k×L+r)×(k×L+r)维的对角阵,矩阵H4’的主对角线上的元素都是“1”;
矩阵H3’是将矩阵H5’中第k×L2+b×L+c列与第b×L2+(c-1)×L+c列进行位置互换而得到的,b的取值范围为0至r-1内的所有整数,c的取值范围为1至L内的所有整数;
矩阵H5’中第1行至k×L行与第1列至k×L2列对应的矩阵等于矩阵H6’,矩阵H5’中第k×L+1行至第k×L+r行与第k×L2+1列至k×L2+r×L列对应的矩阵等于矩阵H7’,矩阵H5’中矩阵H6’和矩阵H7’之外的元素均为“0”;
矩阵H6’为(k×L)×(k×L2)维的矩阵,矩阵H7’为r×(r×L)维的矩阵,矩阵H6’等于矩阵H3,在矩阵H7’中,每行中元素“1”的数量为L,每列中元素“1”的数量等于1,每行的L个元素“1”是连续的。
可选的,处理器1201采用的所述LDPC校验矩阵,例如可以为矩阵H。
可选的,处理器1201采用的所述LDPC校验矩阵,例如可以是对矩阵H进行行置换和/或列置换而得到的。
图12所示的解码器可以用于实现图10所示的基于校验矩阵的装置另外,图12所示的解码器可以用于执行图8所示的方法。
需要说明的是,本发明实施例中的处理器可能是一种集成电路芯片,具有信号的处理能力。在实现过程中,上述方法的各步骤可以通过处理器中的硬件的集成逻辑电路或者软件形式的指令完成。这些指令可以通过其中的处 理器以配合实现及控制,用于执行本发明实施例揭示的方法。上述处理器还可以是通用处理器、数字信号处理器(Digital Signal Processing,DSP)、专用集成电路(application specific integrated circuit)、现成可编程门阵列(Field Programmable Gate Array,FPGA)或者其他可编程逻辑器件、分立门或者晶体管逻辑器件、分立硬件组件。
其中,上述通用处理器可以是微处理器或者该处理器也可以是任何常规的处理器,解码器等。结合本发明实施例所公开的方法的步骤可以直接体现为硬件处理器执行完成,或者用处理器中的硬件及软件模块组合执行完成。软件模块可以位于随机存储器,闪存、只读存储器,可编程只读存储器或者电可擦写可编程存储器、寄存器等本领域成熟的存储介质中。
另外,需要说明的是,总线系统除了包括数据总线之外,还可包括电源总线、控制总线和状态信号总线。但是为了清楚说明起见,在图8、9中将各种总线都标为总线系统。
通过以上的实施方式的描述可知,本领域的技术人员可以清楚地了解到上述实施例方法中的全部或部分步骤可借助软件加通用硬件平台的方式来实现。基于这样的理解,本发明的技术方案本质上或者说对现有技术做出贡献的部分可以以软件产品的形式体现出来,该计算机软件产品可以存储在存储介质中,如ROM/RAM、磁碟、光盘等,包括若干指令用以使得一台计算机设备(可以是个人计算机,服务器,或者诸如媒体网关等网络通信设备)执行本发明各个实施例或者实施例的某些部分所述的方法。
需要说明的是,本说明书中的各个实施例均采用递进的方式描述,各个实施例之间相同相似的部分互相参见即可,每个实施例重点说明的都是与其他实施例的不同之处。尤其,对于方法实施例和设备实施例而言,由于其基本相似于系统实施例,所以描述得比较简单,相关之处参见系统实施例的部分说明即可。以上所描述的设备及系统实施例仅仅是示意性的,其中作为分离部件说明的模块可以是或者也可以不是物理上分开的,作为模块显示的部件可以是或者也可以不是物理模块,即可以位于一个地方,或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部模块来实现本实施例方案的目的。本领域普通技术人员在不付出创造性劳动的情况下, 即可以理解并实施。
以上所述仅是本发明的优选实施方式,并非用于限定本发明的保护范围。应当指出,对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以作出若干改进和润饰,这些改进和润饰也应视为本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!