射频接收机及其射频信号处理方法及装置与流程
本发明涉及无线通信
技术领域:
,特别是涉及一种射频接收机及其射频信号处理方法及装置。
背景技术:
:射频接收机(RadioFrequencyreceiver)需要对接收到的信号进行混频。射频信号混频时,当中频频率小于射频输入载波频段(band)的1/2时,会有镜像落在接收信号所在的频道(channel)内。因此,射频接收机尤其是低中频射频接收机需要采取措施来抑制混频过程中产生的镜像信号。现有的镜像抑制方法有Hartley和Weaver结构。此外,多相滤波器(polyphasefilter)、∑-Δmodulator(ADC)、以及数字自适应滤波器等方法,也被用于镜像抑制。对于在数字部分进行失真补偿的方案,现有技术中通常是数字中频补偿(即在数字部分中频进行失真补偿)。从理论推导的角度来看,数字基带补偿(即在数字部分基带进行失真补偿)理论上也可以抑制混频过程中产生的镜像信号。但数字基带补偿涉及复杂的数学运算,尤其是涉及浮点数的运算,且这些运算需要由接收机来完成。出于成本等因素的考虑,目前绝大多数的接收机通常仅支持定点数的运算,而并不支持浮点数的运算。基于上述原因,尽管数字基带补偿理论上也可以抑制混频过程中产生的镜像信号,但现有技术无法将数字基带补偿应用于不支持浮点数运算的接收机上,来抑制混频过程中产生的镜像信号。技术实现要素:本发明解决的技术问题是:对于不支持浮点数运算的射频接收机,如何抑制混频过程中产生的镜像信号。为了解决上述技术问题,本发明实施例提供一种射频信号处理方法,包括:计算接收到的射频信号与失真补偿后得到的信号之间的关系;对实际接收到的射频信号进行复数混频;对所述进行复数混频后输出的信号进行带通滤波;将所述进行带通滤波后输出的信号转换为数字信号;将所述转换为数字信号后得到的信号在数字域频谱搬移,并进行低通滤波;依据所述射频信号与失真补偿后得到的信号之间的关系、以及所述实际接收到的射频信号,计算实际失真补偿后得到的信号,以所述实际失真补偿后得到的信号作为输出信号;输出所述实际失真补偿后得到的信号。可选的,所述复数混频为两路混频或两路以上混频,所述进行复数混频后输出的信号包括至少两路。可选的,所述计算接收到的射频信号与失真补偿后得到的信号之间的关系包括:计算接收到的射频信号进行复数混频后输出的信号;计算复数混频后输出的信号进行带通滤波后输出的信号;计算带通滤波后输出的信号转换为数字信号后输出的信号;计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号;依据所述低通滤波后输出的信号,计算失真估计值;依据所述失真估计值计算失真补偿值;依据所述失真补偿值计算失真补偿后得到的信号。可选的,所述计算接收到的射频信号进行复数混频后输出的信号包括:令接收到的射频信号为式37:xsig(t)=xbb(t)·cos(ωct),设所述接收机晶振的幅度失真为ε,相位失真为φ,令:K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>则用于进行所述复数混频的信号为式38:cLO(t)=cos(ω1t)-j·(1+ϵ)sin(ω1t+φ)=K1·e-jωLot+K2·ejωLot]]>其中,本振信号频率为:ωLo=fc+fIF,所述本振信号频率为上变频频率。可选的,所述计算复数混频后输出的信号进行带通滤波后输出的信号包括:对所述复数混频后输出的信号进行带通滤波后,输出的信号为式39:rIF(t)=K1s(t)e-jwIFt+K1i(t)ejwIFt+K2s*(t)ejwIFt+K2i*(t)e-jwIFt.]]>可选的,所述计算带通滤波后输出的信号转换为数字信号后输出的信号包括:所述转换为数字信号后输出的信号为式40:r~IF(n)=r~IF,i(n)+j·r~IF,q(n).]]>可选的,所述计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号包括:所述进行低通滤波后得到d(n)为式41:d(n)=LPF{r~IF(n)·ejnωIF}=LPF{K1s(n)+K1i(n)ej2nωIF+K2s*(n)ej2nωIF+K2i*(n)}=K1s(n)+K2i*(n)]]>所述进行低通滤波后得到v(n)为式42:v(n)=LPF{r~IF(n)·e-jnωIF}=LPF{K1s(n)e-j2nωIF+K1i(n)+K2s*(n)+K2i*(n)e-j2nωIF}=K1i(n)+K2s*(n).]]>可选的,所述依据所述低通滤波后输出的信号,计算失真估计值包括:由d(n)和v(n)得到式43:d(n)v*(n)=Ks(n)i*(n)]]>其中,K=K1K2K2*K1*]]>为所述失真估计值,K1+K2*=K1*+K2=1.]]>可选的,所述依据所述失真估计值计算失真补偿值包括:由式43:d(n)v*(n)=Ks(n)i*(n)]]>当ε≠-1,或ε≠0且φ≠0时,K满秩,由式43得到式44:s^(n)i^*(n)=K^-1d(n)v*(n)]]>为对K的估计,所述失真补偿值为:K^-1=1||K1||2-||K2||2·K^1*-K^2-K^2*K^1.]]>可选的,所述依据所述失真补偿值计算失真补偿后得到的信号包括:计算K1K2;计算g1和g2,其中,所述g1和g2均为中间变量;计算进行失真补偿之后得到的信号。可选的,所述计算K1K2包括:由:E{d(n)v(n)}=K1K2E{s(n)s*(n)}+K1K2E{i(n)i*(n)}+K12E{s(n)i(n)}+K22E{s*(n)i*(n)}=K1K2(Ps(n)Pi(n))E{||d(n)+v*(n)||2}=E{||s(n)+i*(n)||2}=E{s(n)s*(n)}+E{i(n)i*(n)}+E{s(n)i(n)}+E{s*(n)i*(n)}=(Ps(n)Pi(n))计算得出式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}.]]>可选的,所述计算g1和g2包括:由K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>以及式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}.]]>计算得到式46:K1K2=14{[1-(1+ϵ)2]-j·2(1+ϵ)sinφ};]]>由式46和式39计算得到式47:g1=(1+ε)sinφ=-2·Im{K1K2}由式46和式39计算得到式48:g2=(1+ϵ)cosφ=1-4·Re{K1K2}-g12=1-4y≈1-2y-2y2-4y3;]]>其中,y=Re{K1K2}+(Im{K1K2})2。可选的,所述计算进行失真补偿之后得到的信号包括:由式47和式48计算得到式49:K^1=1+(1+ϵ)·e-jφ2=12·(1+g2-j·g1)]]>式50:K^2=1-(1+ϵ)·ejφ2=12·(1-g2-j·g1)]]>式51:||K^1||2-||K^2||2=(1+ϵ)cosφ=g2]]>由式49、式50和式51计算得到式52:s^(n)=1||K1||2-||K2||2·[K^1*·d(n)-K^2·v*(n)]=c·[(1+g2+j·g1)·d(n)-(1-g2-j·g1)·v*(n)]]]>其中,为失真补偿后得到的信号。为了解决上述技术问题,本发明实施例还提供一种射频接收机的射频信号处理装置,包括:第一计算单元、混频单元、带通滤波单元、模数转换单元、低通滤波单元、第二计算单元和输出单元;其中:第一计算单元,用于接收到的射频信号与失真补偿后得到的信号之间的关系;混频单元,用于对实际接收到的射频信号进行复数混频;带通滤波单元,用于对所述进行复数混频后输出的信号进行带通滤波;模数转换单元,用于将所述进行带通滤波后输出的信号转换为数字信号;低通滤波单元,用于将所述转换为数字信号后得到的信号在数字域频谱搬移,并进行低通滤波;第二计算单元,用于依据所述射频信号与失真补偿后得到的信号之间的关系、以及所述实际接收到的射频信号,计算实际失真补偿后得到的信号,以所述实际失真补偿后得到的信号作为输出信号;输出单元,用于输出所述实际失真补偿后得到的信号。可选的,所述复数混频为两路混频或两路以上混频,所述进行复数混频后输出的信号包括至少两路。可选的,所述计算接收到的射频信号与失真补偿后得到的信号之间的关系包括:计算接收到的射频信号进行复数混频后输出的信号;计算复数混频后输出的信号进行带通滤波后输出的信号;计算带通滤波后输出的信号转换为数字信号后输出的信号;计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号;依据所述低通滤波后输出的信号,计算失真估计值;依据所述失真估计值计算失真补偿值;依据所述失真补偿值计算失真补偿后得到的信号。可选的,所述计算接收到的射频信号进行复数混频后输出的信号包括:令接收到的射频信号为式37:xsig(t)=xbb(t)·cos(ωct),设所述接收机晶振的幅度失真为ε,相位失真为φ,令:K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>则用于进行所述复数混频的信号为式38:xLO(t)=cos(ω1t)-j·(1+ϵ)sin(ω1t+φ)=K1·e-jωLot+K2·ejωLot]]>其中,本振信号频率为:ωLo=fc+fIF,所述本振信号频率为上变频频率。可选的,所述计算复数混频后输出的信号进行带通滤波后输出的信号包括:对所述复数混频后输出的信号进行带通滤波后,输出的信号为式39:rIF(t)=K1s(t)e-jwIFt+K1i(t)ejwIFt+K2s*(t)ejwIFt+K2i*(t)e-jwIFt.]]>可选的,所述计算带通滤波后输出的信号转换为数字信号后输出的信号包括:所述转换为数字信号后输出的信号为式40:r~IF(n)=r~IF,i(n)+j·r~IF,q(n).]]>可选的,所述计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号包括:所述进行低通滤波后得到d(n)为式41:d(n)=LPF{r~IF(n)·ejnωIF}=LPF{K1s(n)+K1i(n)ej2nωIF+K2s*(n)ej2nωIF+K2i*(n)}=K1s(n)+K2i*(n)]]>所述进行低通滤波后得到v(n)为式42:v(n)=LPF{r~IF(n)·e-jnωIF}=LPF{K1s(n)e-j2nωIF+K1i(n)+K2s*(n)+K2i*(n)e-j2nωIF}=K1i(n)+K2s*(n).]]>可选的,所述依据所述低通滤波后输出的信号,计算失真估计值包括:由d(n)和v(n)得到式43:d(n)v*(n)=Ks(n)i*(n)]]>其中,K=K1K2K2*K1*]]>为所述失真估计值,K1+K2*=K1*+K2=1.]]>可选的,所述依据所述失真估计值计算失真补偿值包括:由式43:d(n)v*(n)=Ks(n)i*(n)]]>当ε≠-1,或ε≠0且φ≠0时,K满秩,由式43得到式44:s^(n)i^*(n)=K^-1d(n)v*(n)]]>为对K的估计,所述失真补偿值为:K^-1=1||K1||2-||K2||2·K^1*-K^2-K^2*K^1.]]>可选的,所述依据所述失真补偿值计算失真补偿后得到的信号包括:计算K1K2;计算g1和g2,其中,所述g1和g2均为中间变量;计算进行失真补偿之后得到的信号。可选的,所述计算K1K2包括:由:E{d(n)v(n)}=K1K2E{s(n)s*(n)}+K1K2E{i(n)i*(n)}+K12E{s(n)i(n)}+K22E{s*(n)i*(n)}=K1K2(Ps(n)Pi(n))E{||d(n)+v*(n)||2}=E{||s(n)+i*(n)||2}=E{s(n)s*(n)}+E{i(n)i*(n)}+E{s(n)i(n)}+E{s*(n)i*(n)}=(Ps(n)Pi(n))计算得出式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}.]]>可选的,所述计算g1和g2包括:由K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>以及式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}]]>计算得到式46:K1K2=14{[1-(1+ϵ)2]-j·2(1+ϵ)sinφ};]]>由式46和式39计算得到式47:g1=(1+ε)sinφ=-2·Im{K1K2}由式46和式39计算得到式48:g2=(1+ϵ)cosφ=1-4·Re{K1K2}-g12=1-4y≈1-2y-2y2-4y3;]]>其中,y=Re{K1K2}+(Im{K1K2})2。可选的,所述计算进行失真补偿之后得到的信号包括:由式47和式48计算得到式49:K^1=1+(1+ϵ)·e-jφ2=12·(1+g2-j·g1)]]>式50:K^2=1-(1+ϵ)·ejφ2=12·(1-g2-j·g1)]]>式51:||K^1||2-||K^2||2=(1+ϵ)cosφ=g2]]>由式49、式50和式51计算得到式52:s^(n)=1||K1||2-||K2||2·[K^1*·d(n)-K^2·v*(n)]=c·[(1+g2+j·g1)·d(n)-(1-g2-j·g1)·v*(n)]]]>其中,为失真补偿后得到的信号。为了解决上述技术问题,本发明实施例还提供一种射频接收机,所述射频接收机包括上述射频接收机的射频信号处理装置。可选的,所述射频接收机能够接收并播放中低频信号。与现有技术相比,本发明的技术方案具有以下有益效果:对于射频接收机,尤其是低中频接收机,在数字部分基带进行失真补偿,能够抑制混频过程中产生的镜像信号,对于部分信号特性的接收信号而言,其算法性能以及补偿后信号镜像比优于现有的(数字中频)补偿方案。进一步地,对计算失真补偿后得到的信号的运算过程进行了改进,改进后的运算过程仅涉及定点数的运算,而不涉及浮点数的运算,也就是说,改进后的算法可以由那些仅支持定点数运算而不支持浮点数运算的接收机完成,从而能够将数字基带补偿应用于不支持浮点数运算的接收机上。附图说明图1为低中频射频接收机上变频混频后频谱示意图;图2为不同晶振幅度失真、相位失真对应的镜像信号比示意图;图3为低中频射频接收机信号处理前端及模数转换示意图;图4为数字部分失真估计结构示意图;图5为各阶段频谱示意图;图6为数字中频补偿失真示意图;图7为数字基带补偿失真示意图;图8为本发明实施例中射频接收机的射频信号处理方法流程图;图9为本发明实施例中射频信号与失真补偿后得到的信号之间关系的计算方法流程图;图10为本发明实施例中射频接收机的射频信号处理装置结构框图;图11为射频接收机数字部分补偿失真结构示意图;图12为算法性能分析中y与失真之间的关系示意图;图13为算法性能分析中失真补偿后得到的信号的信号镜像比与晶振幅度失真之间的关系示意图。具体实施方式正如
背景技术:
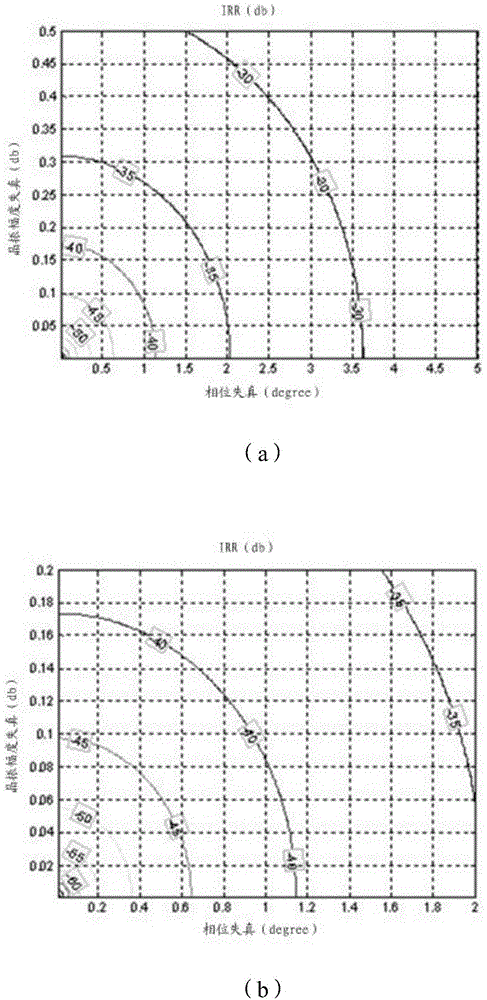
部分所指出的,射频接收机(RadioFrequencyreceiver)需要对接收到的信号进行混频。射频信号混频时,当中频频率小于射频输入载波频段(band)的1/2时,会有镜像落在接收信号所在的频道(channel)内。因此,射频接收机尤其是低中频射频接收机需要采取措施来抑制混频过程中产生的镜像信号。发明人对低中频射频接收机产生失真(混频过程中产生镜像信号)的原因进行分析如下:设发送端基带信号为:xbb(t)=xi(t)+j·xq(t)1则,天线端发送的信号为:xRF,tx(t)=real(xbb(t)·exp(jωct))=xi(t)·cos(ωct)-xq(t)·sin(ωct)2其中,ωc为载波角频率。若不考虑噪声,则接收端射频天线接收到的信号为:xsig(t)=xbb(t)·cos(ωct)3用于混频的本振信号为:xosc(t)=cos(ω1t)-j·sin(ω1t)4其中,ω1为本振信号频率,具体可以是上变频频率,也可以是下变频频率。现在考虑本振信号的晶振幅度失真和相位失真。设晶振幅度失真为ε,相位失真为φ,为了便于后续的计算和分析,令:K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2---6]]>则式4可改写为:xosc(t)=cos(ω1t)-j·(1+ϵ)sin(ω1t+φ)=K1·e-jω1t+K2·ejω1t---5]]>如图1所示,为低中频射频接收机上变频混频后的频谱。其中,(a)为考虑了晶振幅度失真和相位失真后的本振频谱,假如没有晶振幅度失真和相位失真,则K2=0,即ω1处频谱分量为0。(b)给出了接收到的信号(desiredsidebands)和镜像(undesiredimages)的频谱。(c)和(d)分别给出了被和搬移后的信号和镜像的频谱。混频后的频谱为(c)+(d)。(c)中标出的加粗部分是想要得到的信号(Desiredsignal)。由图1可以看出,如果对接收信号复数混频(例如两路混频),且本振信号没有晶振幅度失真和相位失真,则接收带宽内负频谱部分没有镜像。也就是说,晶振幅度失真和相位失真导致接收带宽内负频谱部分出现镜像,正频谱部分出现信号。对于低中频射频接收机下变频混频后的频谱,则(c)中想要得到的信号出现在正频谱部分。继续参考图1,在接收带宽内的负频谱部分,镜像信号比(ImageSignalRate,ISR)为:ISR=10·log10(||K1||2||K2||2)=10·log10(||1-(1+ϵ)·e-jφ||2||1+(1+ϵ)·ejφ||2)---7]]>ε和φ的值都比较小,上式可简化为:ISR≈10·log10(ϵ2+φ2+ϵφ24+ϵ2-φ2+4ϵ-ϵφ2)---8]]>如果ε<<1,φ<<1rad,上式可进一步简化为:ISR≈10·log10(ϵ2+φ24)---9]]>图2给出了不同晶振幅度失真(dB)、相位失真(degree)对应的ISR(dB),其中,图2(a)中相位失真为5°,图2(b)中相位失真为2°。基于上述原因,低中频射频接收机中,晶振幅度失真(amplitudemismatch)和相位失真(phasemismatch)会引起镜像。由图1可以看出,前端晶振幅度失真和相位失真导致接收带宽内负频谱部分出现镜像,正频谱部分出现信号。发明人认为,镜像抑制可以考虑以下三个方面(针对上变频混频的情况):a.降低进入混频器的镜像频道(imagechannel)的强度;b.滤除混频器之后频谱带宽内正频谱部分(镜像为主);c.减少混频器之后频谱带宽内负频谱部分的镜像成分。其中,混频后的镜像抑制性能受制于b和c中的弱项。也就是说,当本振的失真造成的负频谱上信号和镜像的比值大于正频谱上镜像的抑制能力时,受制于正频谱上镜像的抑制能力;当本振的失真造成的负频谱上信号和镜像的比值小于正频谱上镜像的抑制能力时,受制于本振的失真。现有技术中的采用多项滤波器的镜像抑制方法。其主要作用是滤除混频器之后频谱带宽内正频谱部分(镜像为主),即对应于上述方面b。如图3所示,如果在混频后分两路过ADC(Analogue-to-DigitalConverter,模数转换器),可以在数字域滤除不想要的正频谱信号(数字域将频谱搬移到 基带,再通过一个低通滤波器)。但是由于两路分别经过PGA和ADC,两路的增益会不一样。设两路PGA增益的差异为εPGA,两路ADC增益的差异为εAD,因此前端总的失真包括晶振幅度失真ε和相位失真φ,其中,ε=εLO+εPGA+εAD。下面再来讨论三个方面中的a和c。关于a.降低进入混频器的镜像频道(imagechannel)的强度:在混频前可采用模拟预滤波(pre-filter),对镜像频道的强度做一定的衰减。假如预滤波能够在镜像频道有20~30dB的衰减,则数字滤波器能很好地滤除正频谱部分。若前端总的晶振幅度失真ε和相位失真φ做得比较好,使得负频谱上信号和镜像的比值达到40dB,那么总的镜像抑制就能做到60~70dB。假如预滤波达不到足够的衰减,或前端总的晶振幅度失真ε和相位失真φ达不到系统镜像抑制(imagerejection)的性能要求,那么只能尝试数字方案或数字模拟相结合的方案来减少负频谱内的镜像分量。关于c.减少混频器之后频谱带宽内负频谱部分的镜像成分:要减少混频器之后频谱负频谱部分的镜像成分,可以用数字的方法对失真做估计,并在模拟部分或数字部分补偿失真,也可以用数字的方法,不估计失真,盲抵消镜像。如图4所示,为数字部分估计失真所采用的结构。信号经过混频器,由ADC后的数字部分可以估计出前端总的ε和φ。先将图1中的混频输出经过带通滤波器(Band-PassFilter,BPF)后,可以写成:rIF(t)=K1s(t)e-jwIFt+K1i(t)ejwIFt+K2s*(t)ejwIFt+K2i*(t)e-jwIFt---10]]>rIF(t)经过两路ADC,得到r~IF(n)=r~IF,i(n)+j·r~IF,q(n)]]>将在数字域频谱搬移,并经过低通滤波器(两路可以采用同一个低通滤波器),分别得到d(n)和v(n)如下:d(n)=LPF{r~IF(n)·ejnωIF}=LPF{K1s(n)+K1i(n)ej2nωIF+K2s*(n)ej2nωIF+K2i*(n)}=K1s(n)+K2i*(n)---11]]>v(n)=LPF{r~IF(n)·e-jnωIF}=LPF{K1s(n)e-j2nωIF+K1i(n)+K2s*(n)+K2i*(n)e-j2nωIF}=K1i(n)+K2s*(n)---12]]>各阶段信号频谱如图5所示,其中,AfterMixer表示经混频后,AfterADC表示经模数转换后。由式11和式12,可以得到不同的失真估计方法。可以通过如下方法直接计算失真:由式11和式12可得:d(n)v(n)=LK1K2---13]]>其中,L=s(n)i*(n)i(n)s*(n)]]>由式13可得,当||s(n)||2≠||i(n)||2时,K1K2=1||s(n)||2-||i(n)||2·s(n)d(n)-i*(n)v(n)-i(n)d(n)+s*(n)v(n)---14]]>由先前的式5可推得从而得到:φ=12j·ln(1-2K22K1-1)---15]]>ϵ=(2K1-1)1-2K22K1-1-1---16]]>其中,式14中用到了s(n),在实际使用中,测试信号(testtone)的幅度较难直接得到,且这种方法不利于做统计(前端还是有噪声,失真估计时要统计平均),因此,这种方法不可取。以下提供两种可行的失真估计方法,都是基于d(n)和v(n),但具体的估计方法不一样。其中,方法一中做了近似,而方法二的理论推导比较严密,但 运算量大。使用实施例一或实施例二时都需要进行一定数量样本的统计平均,样本数量将影响信噪比。方法一:设u1=real{d(n)},u2=imag{d(n)},u′1=real{v(n)},u′2=-imag{v(n)};得到:u1u2′-u1′u2u12+u22=-Im{d(n)v(n)}||d(n)||2---17]]>u1u1′+u2u2′u12+u22=Re{d(n)v(n)}||d(n)||2---18]]>当i(n)=0时,式17和式18推导如下:u1u2′u12+u22=-Im{d(n)v(n)}||d(n)||2=-Im{K1K2}||K1||2=4(1+ϵ)sinφ2cosφ24(1+ϵ)cos2φ2+ϵ2≈tanφ2---19]]>u1u1′+u2u2′u12+u22=Re{d(n)v(n)}||d(n)||2=Re{K1K2}||K1||2=-2ϵ-ϵ24(1+ϵ)cos2φ2+ϵ2≈-ϵ2---20]]>由式19和式20得到:φ=2·atan(u1u2′-u1′u2u12+u22)---21]]>ϵ=-2·u1u1′+u2u2′u12+u22---22]]>方法二:由式11和式12,可得:d(n)v*(n)=Ks(n)i*(n),---23]]>其中K=K1K2K2*K1*,K1+K2*=K1*+K2=1]]>由式11和式12考虑期望:E{d(n)v(n)}=K1K2·E{s(n)s*(n)}+K1K2·E{i(n)i*(n)}+K12·E{s(n)i(n)}+K22·E{s*(n)i*(n)}=K1K2(Ps+Pn)---24]]>因为K1+K2*=K1*+K2=1,]]>E{||d(n)+v*(n)||2}=E{||(K1+K2*)·s(n)+(K1*+K2)·i*(n)||2}=E{||s(n)+i*(n)||2}=E{||s(n)||2}+E{||i*(n)||2}+E{s(n)i(n)}+E{i*(n)i*(n)}=Ps+Pn---25]]>由式24和式25得:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}---26]]>由先前的式5得:K1K2=14{[1-(1+ϵ)2]-j·2(1+ϵ)sinφ}---27]]>由式27可得:ϵ=1-4·Re{K1K2}-1---28]]>φ=arcsin(-2(1+ϵ)·Im{K1K2})---29]]>式28和式29估计除了模拟前端的失真。式29中,如果ε和φ较小,可做简化,式29也可写成atan的形式,但要增加开根号的运算。由估计出的模拟前端的失真,根据式5可以计算出和在数字部分进行了失真估计之后,在模拟部分或数字部分补偿前端的失真。具体地:可以在数字部分估计前端的失真,反馈给模拟前端。如果可以外灌或内部生成模拟的测试信号(testtone),将测试信号经过混频器,由ADC后的数字部分可以估计出前端总的ε和φ,并反馈到前端进行校正。校正后,ε和φ变小,负频谱部分的镜像成分也就变少了。从而提高了接收机镜像抑制的性能。这个方法需要同时满足如下3个条件:条件1、接收机信号带宽内ε和φ比较稳定;条件2、在一定时间内(AM系统应该是停留在某一个台的时间内)比较稳定,或接收机是TDD系统(有一定的时间空闲,可以重新灌入测试信号,AM接收机不满足次条件);条件3、ε和φ在一定温度范围内比较稳定。可以基于先前给出的两种数字部分的失真估计方法(即方法一和方法二),由估计出的模拟前端的失真,在数字部分进行补偿。以下提供两种可行的数字部分的失真补偿方法(方法三和方法四)。补偿可以通过在开机时生成模拟信号,灌入接收机来计算失真。在之后实际接收信号的过程中使用此计算结果来实现。补偿也可以通过实时计算失真并补偿来实现。方法三:数字中频补偿失真如图6所示,ADC后通过α和β进行补偿,最终输出d(n)路。可以认为α和β是直接对本振进行补偿。用于混频的本振信号为:xosc(t)=cos(ω1t)-j(1+ε)sin(ω1t+φ)补偿α和β后为:x′osc(t)=cos(ω1t)-j(βcos(ω1t)+α(1+ε)sin(ω1t+φ))30=cos(ω1t)-j[(β+α(1+ε)sinφ)cos(ω1t)+α(1+ε)cosφsin(ω1t)]补偿后需满足:α(1+ε)cosφ=131(β+α(1+ε)sinφ)=032式31和32即:α=1(1+ϵ)cosφ---33]]>β=-tanφ34方法四:数字基带补偿失真如图7所示,基带对d(n)和v(n)做运算,最终输出路。估计出ε和φ后(可以由前述的方法一或方法二估计出ε和φ),可根据式5可以计算出和即得到当ε≠-1,或ε≠0且φ≠0时,K满秩,由式19可得到:s^(n)i^*(n)=K^-1d(n)v*(n)---35]]>也可以通过下面的式子来估计:s^(n)i^*(n)=(K^HK^)-1K^Hd(n)v*(n)---36]]>其中,为最终输出信号。正如
背景技术:
部分所分析的,对于在数字部分进行失真补偿的方案,现有技术中通常是数字中频补偿(即在数字部分中频进行失真补偿)。从理论推导的角度来看,数字基带补偿(即在数字部分基带进行失真补偿)理论上也可以抑制混频过程中产生的镜像信号。但数字基带补偿涉及复杂的数学运算,尤其是涉及浮点数的运算,且这些运算需要由接收机来完成。出于成本等因素的考虑,目前绝大多数的接收机通常仅支持定点数的运算,而并不支持浮点数的运算。基于上述原因,尽管数字基带补偿理论上也可以抑制混频过程中产生的 镜像信号,但现有技术无法将数字基带补偿应用于不支持浮点数运算的接收机上,来抑制混频过程中产生的镜像信号。发明人经研究后发现:数字基带补偿的理论推导过程中,涉及浮点数的运算体现在计算失真补偿后得到的信号的过程中。发明人对计算失真补偿后得到的信号的运算过程进行了改进,改进后的运算过程仅涉及定点数的运算,而不涉及浮点数的运算。也就是说,改进后的算法可以由那些仅支持定点数运算而不支持浮点数运算的接收机完成,从而能够将数字基带补偿应用于不支持浮点数运算的接收机上,对于部分信号特性的接收信号而言,其算法性能以及补偿后信号镜像比优于现有的补偿方案。为使本领域技术人员更好地理解和实现本发明,以下参照附图,通过具体实施例进行详细说明。实施例一如下所述,本发明实施例提供一种射频接收机的射频信号处理方法。参照图8所示的射频接收机的射频信号处理方法流程图,以下通过具体步骤进行详细说明:S801,计算接收到的射频信号与失真补偿后得到的信号之间的关系。参照图9所示的射频信号与失真补偿后得到的信号之间关系的计算方法流程图,所述计算接收到的射频信号与失真补偿后得到的信号之间的关系具体可以包括:S901,计算接收到的射频信号进行复数混频后输出的信号;S902,计算复数混频后输出的信号进行带通滤波后输出的信号;S903,计算带通滤波后输出的信号转换为数字信号后输出的信号;S904,计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号;S905,依据所述低通滤波后输出的信号,计算失真估计值;S906,依据所述失真估计值计算失真补偿值;S907,依据所述失真补偿值计算失真补偿后得到的信号。不考虑模拟部分和数字部分前端的具体实现形式。如图11所示,为本发明实施例提供的一种射频接收机的射频信号处理方法示意图。其中:S901,计算接收到的射频信号进行复数混频后输出的信号包括:令接收到的射频信号为式37:xsig(t)=xbb(t)·cos(ωct),设所述接收机晶振的幅度失真为ε,相位失真为φ,令:K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>则用于进行所述复数混频的信号为式38:xLO(t)=cos(ω1t)-j·(1+ϵ)sin(ω1t+φ)=K1·e-jωLot+K2·ejωLot]]>其中,本振信号频率为:ωLo=fc+fIF,所述本振信号频率为上变频频率。S902,计算复数混频后输出的信号进行带通滤波后输出的信号包括:对所述复数混频后输出的信号进行带通滤波后,输出的信号为式39:rIF(t)=K1s(t)e-jwIFt+K1i(t)ejwIFt+K2s*(t)ejwIFt+K2i*(t)e-jwIFt.]]>S903,计算带通滤波后输出的信号转换为数字信号后输出的信号包括:所述转换为数字信号后输出的信号为式40:r~IF(n)=r~IF,i(n)+j·r~IF,q(n).]]>S904,计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号包括:所述进行低通滤波后得到d(n)为式41:d(n)=LPF{r~IF(n)·ejnωIF}=LPF{K1s(n)+K1i(n)ej2nωIF+K2s*(n)ej2nωIF+K2i*(n)}=K1s(n)+K2i*(n)]]>所述进行低通滤波后得到v(n)为式42:v(n)=LPF{r~IF(n)·e-jnωIF}=LPF{K1s(n)e-j2nωIF+K1i(n)+K2s*(n)+K2i*(n)e-j2nωIF}=K1i(n)+K2s*(n).]]>S905,依据所述低通滤波后输出的信号,计算失真估计值包括:由d(n)和v(n)得到式43:d(n)v*(n)=Ks(n)i*(n)]]>其中,K=K1K2K2*K1*]]>为所述失真估计值,K1+K2*=K1*+K2=1.]]>其中,i*(n)为镜像信号。S906,依据所述失真估计值计算失真补偿值包括:由式43:d(n)v*(n)=Ks(n)i*(n)]]>当ε≠-1,或ε≠0且φ≠0时,K满秩,由式43得到式44:s^(n)i^*(n)=K^-1d(n)v*(n)]]>为对K的估计,所述失真补偿值为:K^-1=1||K1||2-||K2||2·K^1*-K^2-K^2*K^1.]]>S907,依据所述失真补偿值计算失真补偿后得到的信号包括:计算K1K2;具体地,所述计算K1K2包括:由:E{d(n)v(n)}=K1K2E{s(n)s*(n)}+K1K2E{i(n)i*(n)}+K12E{s(n)i(n)}+K22E{s*(n)i*(n)}=K1K2(Ps(n)Pi(n))E{||d(n)+v*(n)||2}=E{||s(n)+i*(n)||2}=E{s(n)s*(n)}+E{i(n)i*(n)}+E{s(n)i(n)}+E{s*(n)i*(n)}=(Ps(n)Pi(n))计算得出式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}.]]>计算g1和g2,其中,所述g1和g2均为中间变量;具体地,所述计算g1和g2包括:由K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>以及式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}]]>计算得到式46:K1K2=14{[1-(1+ϵ)2]-j·2(1+ϵ)sinφ};]]>由式46和式39计算得到式47:g1=(1+ε)sinφ=-2·Im{K1K2}由式46和式39计算得到式48:g2=(1+ϵ)cosφ=1-4·Re{K1K2}-g12=1-4y≈1-2y-2y2-4y3;]]>其中,y=Re{K1K2}+(Im{K1K2})2。g1和g2是为了简化运算而引入的中间变量。在计算g2的过程中作了近似,因而该算法最终运算得到的失真补偿后得到的信号与真实值之间不可避免的存在一些误差。后续会对本实施例中算法的算法性能进行分析。计算进行失真补偿之后得到的信号;具体地,所述计算进行失真补偿之后得到的信号包括:由式47和式48计算得到式49:K^1=1+(1+ϵ)·e-jφ2=12·(1+g2-j·g1)]]>式50:K^2=1-(1+ϵ)·ejφ2=12·(1-g2-j·g1)]]>式51:||K^1||2-||K^2||2=(1+ϵ)cosφ=g2]]>由式49、式50和式51计算得到式52:s^(n)=1||K1||2-||K2||2·[K^1*·d(n)-K^2·v*(n)]=c·[(1+g2+j·g1)·d(n)-(1-g2-j·g1)·v*(n)]]]>其中,为失真补偿后得到的信号,c不用计算,在定点时注意位宽即可。上述算法是假设混频器的cos路失真为0。如果要补偿到混频器cos和sin两路的失真的中间值,则该方法可能会存在较大的误差。通过以上对技术方案的描述可以看出:本实施例中,对计算失真补偿后得到的信号的运算过程进行了改进,改进后的运算过程仅涉及定点数的运算,而不涉及浮点数的运算,也就是说,改进后的算法可以由那些仅支持定点数运算而不支持浮点数运算的接收机完成,从而能够将数字基带补偿应用于不支持浮点数运算的接收机上。以下进一步计算残留的信号镜像比IRR:由式43和44得:s^(n)s^*(n)=K^-1d(n)v*(n)=K^-1Ks(n)i*(n)=1||K1||2-||K2||2K^1*K1-K^2K2*K^1*K2-K^2K1*-K^2*K1+K^1K2*-K^2*K2+K^1K1*s(n)i*(n)---53]]>残留的信号镜像比为:IRR=10·log10(||K^1*K1-K^2K2*||2||K^1*K2-K^2K1*||2)---54]]>对本实施例中射频接收机的射频信号处理方法的算法性能进行分析如下:本实施例中射频接收机的射频信号处理方法,其算法性能受制于接收信号的信噪比,用于计算期望的数据长度,及式48中的近似运算。以下分析不考虑噪声,仅考虑式48中的近似运算。y的大小主要取决于晶振幅度失真,如图12所示。式48中近似运算采用到三次项后,补偿后信号镜像比(SignalImageRate,SIR)如图13所示,当晶振幅度失真为1db时,估计并补偿后信号镜像比达到83db。射频接收机以上述步骤S901至步骤S907中的计算接收到的射频信号与失真补偿后得到的信号之间的关系。在此之后,可以依据所述射频信号与失真补偿后得到的信号之间的关系、以及所述实际接收到的射频信号,直接得到待播放信号并播放(参考后续步骤)。在信号特性不发生改变的情况下,无需反复执行上述步骤S901至步骤S907中完整的推导过程。S802,对实际接收到的射频信号进行复数混频。所述复数混频为两路混频或两路以上混频,所述进行复数混频后输出的信号包括至少两路。在一个具体的实施例中,所述复数混频为两路混频,所述进行复数混频后输出的信号包括两路。S803,对所述进行复数混频后输出的信号进行带通滤波。S804,将所述进行带通滤波后输出的信号转换为数字信号。S805,将所述转换为数字信号后得到的信号在数字域频谱搬移,并进行低通滤波。在具体实施中,两路可以采用同一个低通滤波器(Low-PassFilter,LPF)。S806,依据所述射频信号与失真补偿后得到的信号之间的关系、以及所述实际接收到的射频信号,计算实际失真补偿后得到的信号,以所述实际失 真补偿后得到的信号作为输出信号。如前所述,射频接收机可以依据所述射频信号与失真补偿后得到的信号之间的关系、以及所述实际接收到的射频信号,直接得到待播放信号并播放。在信号特性不发生改变的情况下,无需反复执行上述步骤S901至步骤S907中完整的推导过程。S807,输出所述实际失真补偿后得到的信号。在计算出实际失真补偿后得到的信号(即输出信号)后,射频接收机即可以此进行播放。通过以上对技术方案的描述可以看出:本实施例中,对于射频接收机,尤其是低中频接收机,在数字部分基带进行失真补偿,能够抑制混频过程中产生的镜像信号,对于部分信号特性的接收信号而言,其算法性能以及补偿后信号镜像比优于现有的补偿方案。实施例二本发明实施例提供一种射频接收机的射频信号处理装置,包括:第一计算单元1001、混频单元1002、带通滤波单元1003、模数转换单元1004、低通滤波单元1005、第二计算单元1006和输出单元1007;其中各单元的主要功能如下:第一计算单元1001,用于接收到的射频信号与失真补偿后得到的信号之间的关系;混频单元1002,用于对实际接收到的射频信号进行复数混频;带通滤波单元1003,用于对所述进行复数混频后输出的信号进行带通滤波;模数转换单元1004,用于将所述进行带通滤波后输出的信号转换为数字信号;低通滤波单元1005,用于将所述转换为数字信号后得到的信号在数字域频谱搬移,并进行低通滤波;第二计算单元1006,用于依据所述射频信号与失真补偿后得到的信号之 间的关系、以及所述实际接收到的射频信号,计算实际失真补偿后得到的信号,以所述实际失真补偿后得到的信号作为输出信号;输出单元1007,用于输出所述实际失真补偿后得到的信号。通过以上对技术方案的描述可以看出:本实施例中,对于射频接收机,尤其是低中频接收机,在数字部分基带进行失真补偿,能够抑制混频过程中产生的镜像信号,对于部分信号特性的接收信号而言,其算法性能以及补偿后信号镜像比优于现有的补偿方案。在具体实施中,所述复数混频为两路混频或两路以上混频,所述进行复数混频后输出的信号包括至少两路。参照图9所示的射频信号与失真补偿后得到的信号之间关系的计算方法流程图,在具体实施中,所述计算接收到的射频信号与失真补偿后得到的信号之间的关系具体可以包括:S901,计算接收到的射频信号进行复数混频后输出的信号;S902,计算复数混频后输出的信号进行带通滤波后输出的信号;S903,计算带通滤波后输出的信号转换为数字信号后输出的信号;S904,计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号;S905,依据所述低通滤波后输出的信号,计算失真估计值;S906,依据所述失真估计值计算失真补偿值;S907,依据所述失真补偿值计算失真补偿后得到的信号。不考虑模拟部分和数字部分前端的具体实现形式。如图11所示为射频接收机数字部分补偿失真结构示意图。其中:S901,计算接收到的射频信号进行复数混频后输出的信号包括:令接收到的射频信号为式37:xsig(t)=xbb(t)·cos(ωct),设所述接收机晶振的幅度失真为ε,相位失真为φ,令:K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>则用于进行所述复数混频的信号为式38:cLO(t)=cos(ω1t)-j·(1+ϵ)sin(ω1t+φ)=K1·e-jωLot+K2·ejωLot]]>其中,本振信号频率为:ωLo=fc+fIF,所述本振信号频率为上变频频率。S902,计算复数混频后输出的信号进行带通滤波后输出的信号包括:对所述复数混频后输出的信号进行带通滤波后,输出的信号为式39:rIF(t)=K1s(t)e-jwIFt+K1i(t)ejwIFt+K2s*(t)ejwIFt+K2i*(t)e-jwIFt.]]>S903,计算带通滤波后输出的信号转换为数字信号后输出的信号包括:所述转换为数字信号后输出的信号为式40:r~IF(n)=r~IF,i(n)+j·r~IF,q(n).]]>S904,计算转换为数字信号后输出的信号在数字域频谱搬移并进行低通滤波后输出的信号包括:所述进行低通滤波后得到d(n)为式41:d(n)=LPF{r~IF(n)·ejnωIF}=LPF{K1s(n)+K1i(n)ej2nωIF+K2s*(n)ej2nωIF+K2i*(n)}=K1s(n)+K2i*(n)]]>所述进行低通滤波后得到v(n)为式42:v(n)=LPF{r~IF(n)·e-jnωIF}=LPF{K1s(n)e-j2nωIF+K1i(n)+K2s*(n)+K2i*(n)e-j2nωIF}=K1i(n)+K2s*(n).]]>S905,依据所述低通滤波后输出的信号,计算失真估计值包括:由d(n)和v(n)得到式43:d(n)v*(n)=Ks(n)i*(n)]]>其中,K=K1K2K2*K1*]]>为所述失真估计值,K1+K2*=K1*+K2=1.]]>S906,依据所述失真估计值计算失真补偿值包括:由式43:d(n)v*(n)=Ks(n)i*(n)]]>当ε≠-1,或ε≠0且φ≠0时,K满秩,由式43得到式44:s^(n)i^*(n)=K^-1d(n)v*(n)]]>为对K的估计,所述失真补偿值为:K^-1=1||K1||2-||K2||2·K^1*-K^2-K^2*K^1.]]>S907,依据所述失真补偿值计算失真补偿后得到的信号包括:计算K1K2;具体地,所述计算K1K2包括:由:E{d(n)v(n)}=K1K2E{s(n)s*(n)}+K1K2E{i(n)i*(n)}+K12E{s(n)i(n)}+K22E{s*(n)i*(n)}=K1K2(Ps(n)Pi(n))E{||d(n)+v*(n)||2}=E{||s(n)+i*(n)||2}=E{s(n)s*(n)}+E{i(n)i*(n)}+E{s(n)i(n)}+E{s*(n)i*(n)}=(Ps(n)Pi(n))计算得出式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}.]]>计算g1和g2,其中,所述g1和g2均为中间变量;具体地,所述计算g1和g2包括:由K1=1+(1+ϵ)·e-jφ2,K2=1-(1+ϵ)·ejφ2]]>以及式45:K1K2=E{d(n)v(n)}E{||d(n)+v*(n)||2}]]>计算得到式46:K1K2=14{[1-(1+ϵ)2]-j·2(1+ϵ)sinφ};]]>由式46和式39计算得到式47:g1=(1+ε)sinφ=-2·Im{K1K2}由式46和式39计算得到式48:g2=(1+ϵ)cosφ=1-4·Re{K1K2}-g12=1-4y≈1-2y-2y2-4y3;]]>其中,y=Re{K1K2}+(Im{K1K2})2。g1和g2是为了简化运算而引入的中间变量。在计算g2的过程中作了近似,因而该算法最终运算得到的失真补偿后得到的信号与真实值之间不可避免的存在一些误差。计算进行失真补偿之后得到的信号;具体地,所述计算进行失真补偿之后得到的信号包括:由式47和式48计算得到式49:K^1=1+(1+ϵ)·e-jφ2=12·(1+g2-j·g1)]]>式50:K^2=1-(1+ϵ)·ejφ2=12·(1-g2-j·g1)]]>式51:||K^1||2-||K^2||2=(1+ϵ)cosφ=g2]]>由式49、式50和式51计算得到式52:s^(n)=1||K1||2-||K2||2·[K^1*·d(n)-K^2·v*(n)]=c·[(1+g2+j·g1)·d(n)-(1-g2-j·g1)·v*(n)]]]>其中,为失真补偿后得到的信号,c不用计算,在定点时注意位宽即可。上述算法是假设混频器的cos路失真为0。如果要补偿到混频器cos和sin两路的失真的中间值,则该方法可能会存在较大的误差。通过以上对技术方案的描述可以看出:本实施例中,对计算失真补偿后得到的信号的运算过程进行了改进,改进后的运算过程仅涉及定点数的运算,而不涉及浮点数的运算,也就是说,改进后的算法可以由那些仅支持定点数运算而不支持浮点数运算的接收机完成,从而能够将数字基带补偿应用于不支持浮点数运算的接收机上。实施例三如下所述,本实施例提供一种射频接收机。与现有技术的不同之处在于,所述射频接收机包括本发明实施例中所提供的射频接收机的射频信号处理装置。该射频接收机在数字部分基带进行失真补偿,能够抑制混频过程中产生的镜像信号,对于部分信号特性的接收信号而言,其算法性能以及补偿后信号镜像比优于现有的补偿方案。进一步地,对计算失真补偿后得到的信号的运算过程进行了改进,改进后的运算过程仅涉及定点数的运算,而不涉及浮点数的运算,也就是说,改进后的算法可以由那些仅支持定点数运算而不支持浮点数运算的接收机完成,从而能够将数字基带补偿应用于不支持浮点数运算的接收机上。在具体实施中,所述射频接收机能够接收并播放中低频信号。本领域普通技术人员可以理解上述实施例的各种方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成,该程序可以存储于一计算机可读存储介质中,存储介质可以包括:ROM、RAM、磁盘或光盘等。虽然本发明披露如上,但本发明并非限定于此。任何本领域技术人员,在不脱离本发明的精神和范围内,均可作各种更动与修改,因此本发明的保护范围应当以权利要求所限定的范围为准。当前第1页1 2 3
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1