低通信号的双通道TIADC非线性系统参数估计方法与流程

本发明涉及高速的模数转换技术领域，更具体地，涉及一种低通信号的双通道tiadc非线性系统参数估计方法。

背景技术：

随着集成电路技术的不断发展，数字化技术的推广，对模数转换器件adc的采样速率以及采样精度的要求越来越高，不仅要求数据采集系统有高的采样率，还要有高的采样精度。在实际的运用中，对实时采样速率以及采样精度有极高的依赖性。然而adc的最大采样速率受限于它的分辨率,分辨率与采样速率之间是一对矛盾体，根据目前的ic设计工艺，要实现更高速的采样速率，我们需要探索一种基于新结构和新方法的adc。一种实现超高速采样的重要方法就是利用时间交织(time-interleaved)结构的adc。

这种多通道时间交织系统的方法是利用m片有着相同采样率fs的单个adc，采用并行的结构，每片adc以相隔1/(m*fs)的时间间隔进行采样，以达到采样率为m*fs(总采样率f＝m*fs)的效果。理论上，这种对于m通道的并行交替采样的adc结构能够使得整个系统采样率达到单个adc的m倍。但是由于制造工艺本身固有的缺点，不可能使得每一片adc完全一模一样，所以必然会使得各个通道adc之间存在失配误差，从而严重降低了整个adc系统的信噪比。

国内外早期基于多通道时间交织adc系统的失配修正一般是利用对前端电路的修调，通过精心布局的线路来减少失配误差的影响。这种方法的缺点就是当随着时间的推移，温度的变化，电器元件的老化会使得电路的修正效果失效。为了克服这种前端修正的方法，可以利用后端处理的方法，目前基于多通道时间交织adc系统的失配误差及其数字后端处理的修正算法是未来发展的关键。

然而，目前大多数数字后端补偿方法必须针对特定的误差种类如增益误差，时间误差，限制了补偿系统性能的提升。即便是通过通道传递函数把线性滤波器的误差的效果转移为频域响应失配误差，其处理范围仍然把误差限制在线性的范围内。

技术实现要素：

本发明提供一种高效的低通信号的双通道tiadc非线性系统参数估计方法。

为了达到上述技术效果，本发明的技术方案如下：

一种低通信号的双通道tiadc非线性系统参数估计方法，包括以下步骤：

s1：设置各通道的输入信号，使其输入输出满足：其中，x(t)为输入信号，为非线性误差参数，m表示通道号，l表示非线性误差阶数；

s2：设置误差信号：令误差信号为：令s＝[s2，s3...sl]，d＝[d2，d3...dl]，px[n]＝[x²[n],x³[n]...x^l[n]]^t则误差信号为：e[n]＝s[x2[n],x3[n]...xl[n]]^t+(-1)ⁿd[x2[n],x3[n]...xl[n]]^t；

s3：用高通滤波器f[n]对tiadc的输出信号y[n]进行滤波处理，得到的输出信号ed[n]则不包含输入信号的信息，而只含误差信息，故用作误差估计的期望信号；

s4：用y[n]近似代替x[n]，获取(y[n])²、(y[n])³......(y[n])^l，在用高通滤波器f[n]对上述高阶信号进行滤波，所得信号为ys²[n]、ys³[n].......ys^l[n]；

s5:对(y[n])²、(y[n])³......(y[n])^l经过一个(-1)ⁿ的乘法器，再用同一个高通滤波器f[n]对上述高阶信号进行滤波，所得信号为yd²[n]、yd³[n].......yd^l[n]；

s6：以ys²[n]、ys³[n].......ys^l[n]为输入信号，ed[n]为期望信号，s＝[s2，s3...sl]为待估计误差系数，进行变步长的nlms算法；

s7：以yd²[n]、yd³[n].......yd^l[n]，为输入信号，ed[n]为期望信号，d＝[d2，d3...dl]为待估计误差系数，进行变步长的nlms算法；

s8：求解步骤s7中的线性方程即得到各通道非线性系统参数。

进一步地，所述步骤s6的具体过程如下：

s61：设

s62：计算各时刻学习速率：

对于k时刻，输出信号y(k)＝(w|第k-1行)(x|第k行)^t+p|第k行，则估计误差

e(k)＝d(k)-y(k)；

令变步长因子β(k)＝β(k-1)-ρ(k)/σ(k)，其中ρ(k)＝γ*α*c(k)，γ为可以调节的学习速率偏移参数，α为可以调节的步长参数，c(k)＝e(k)e(k-1)×(x|第k行)(x|第k-1行)^t，σ(k)＝(x|第k-1行)(x|第k-1行)^t+β(k-1)则k时刻的学习速率

s63：计算待估计系统参数：

对于k时刻，w|第k行＝w|第k-1行+μ(k)e(k)(x|第k行)^*，则

进一步地，所述步骤s7的具体过程如下：

s71：设

s72：计算各时刻学习速率：

对于k时刻，输出信号y(k)＝(w|第k-1行)(x|第k行)^t+p|第k行，则估计误差e(k)＝d(k)-y(k)；

令变步长因子β(k)＝β(k-1)-ρ(k)/σ(k)，其中ρ(k)＝γ*α*c(k)，γ为可以调节的学习速率偏移参数，α为可以调节的步长参数，c(k)＝e(k)e(k-1)×(x|第k行)(x|第k-1行)^t,σ(k)＝(x|第k-1行)(x|第k-1行)^t+β(k-1)，则k时刻的学习速率

s73：计算待估计系统参数：

对于k时刻，w|第k行＝w|第k-1行+μ(k)e(k)(x|第k行)^*，则

进一步地，所述步骤s8的具体过程如下：

求解线性方程组即求解各通道非线性系统参数。

与现有技术相比，本发明技术方案的有益效果是：

本发明把处理的限制放宽到误差中的非线性部分，误差系数估计的过程中运用了变步长的归一化最小均方误差nlms算法(variablestep-sizenormalizedleastmeansquarealgorithm)进行了优化，从而提高了估计速度，满足了对模数转换器更高的需求。

附图说明

图1为带有非线性传输特性的双通道tiadc模型示意图；

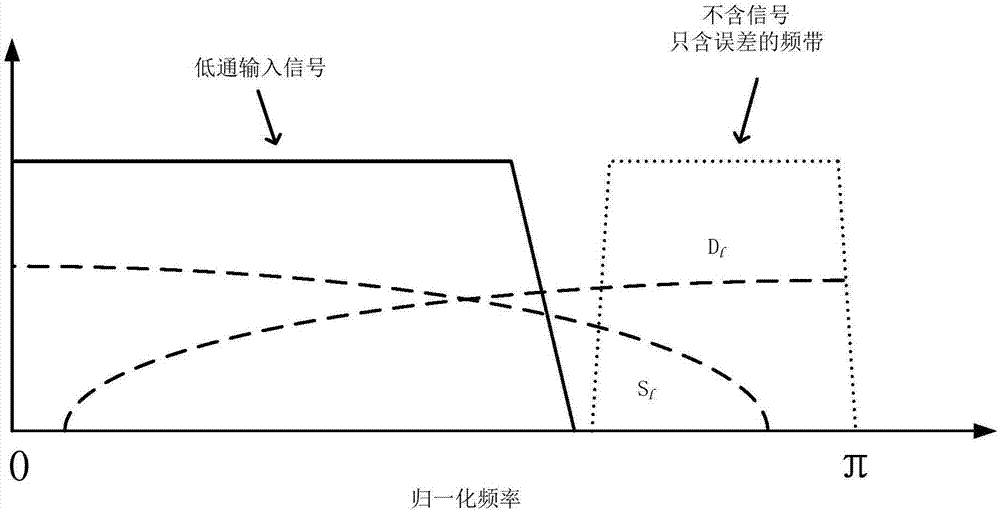
图2为基于低通信号采样的频谱示意图；

图3为基于变步长nlms的s参数估计结构图；

图4为s参数的估计曲线图；

图5为估计的均方误差图(s参数)；

图6为基于变步长nlms的d参数估计结构图；

图7为d参数的估计曲线图；

图8为估计的均方误差图(d参数)。

具体实施方式

附图仅用于示例性说明，不能理解为对本专利的限制；

为了更好说明本实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；

对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。

下面结合附图和实施例对本发明的技术方案做进一步的说明。

实施例1

1.设置输入信号x(t)满足采样定理。对于理想的adc装置，在经过采样保持器之前，各通道的输入输出应该是一致的，即tm(x)＝x(t)。而对于存在非线性误差的传输系统，各通道的输入输出关系就应用来表示，其中为非线性误差参数，m表示通道号，l表示非线性误差阶数。

2.令由于提前经过线性校正处理，一阶误差则误差信号

令s＝[s2，s3...sl]，d＝[d2，d3...dl]，px[n]＝[x²[n],x³[n]...x^l[n]]^t，则误差信号可表示为

e[n]＝s[x2[n],x3[n}...xl[n]]^t+(-1)ⁿd[x2[n],x3[n]...xl[n]]^t

3.设计一个高通滤波器f[n]，使该滤波器的截止频率需要高于低通采样信号的截止频率。并用该滤波器f[n]对tiadc的输出信号y[n]进行滤波处理。其所得的输出信号ed[n]则必然不包含输入信号的信息，而只含误差信息，故用作误差估计的期望信号。

4.用y[n]近似代替x[n]，获取(y[n])²、(y[n])³......(y[n])^l。再用第3步所设计的高通滤波器f[n]对上述高阶信号进行滤波，所得信号为ys²[n]、ys³[n].......ys^l[n]。

5.对(y[n])²、(y[n])³......(y[n])^l经过一个(-1)ⁿ的乘法器，再用同一个高通滤波器f[n]对上述高阶信号进行滤波，所得信号为yd²[n]、yd³[n].......yd^l[n]。

6.以ys²[n]、ys³[n].......ys^l[n]为输入信号，ed[n]为期望信号，s＝[s2，s3...sl]为待估计误差系数，进行变步长的nlms算法。具体操作如下：

(1)设

(2)计算各时刻学习速率。

对于k时刻，输出信号y(k)＝(w|第k-1行)(x|第k行)^t+p|第k行，则估计误差e(k)＝d(k)-y(k)。

令变步长因子β(k)＝β(k-1)-ρ(k)/σ(k)，

其中ρ(k)＝γ*α*c(k)，γ为可以调节的学习速率偏移参数，α为可以

调节的步长参数，c(k)＝e(k)e(k-1)×(x|第k行)(x|第k-1行)^t,

σ(k)＝(x|第k-1行)(x|第k-1行)^t+β(k-1)

则k时刻的学习速率

(3)计算待估计系统参数。

对于k时刻，w|第k行＝w|第k-1行+μ(k)e(k)(x|第k行)^*

则

7.相似地，以yd²[n]、yd³[n].......yd^l[n]，为输入信号，ed[n]为期望信号，d＝[d2，d3...dl]为待估计误差系数，进行变步长的nlms算法。具体操作如下：

(1)设

(2)仿照第6步(2)，计算各时刻学习速率。

对于k时刻，输出信号y(k)＝(w|第k-1行)(x|第k行)^t+p|第k行，则估计误差e(k)＝d(k)-y(k)。

令变步长因子β(k)＝β(k-1)-ρ(k)/σ(k)，

其中ρ(k)＝γ*α*c(k)，γ为可以调节的学习速率偏移参数，α为可以

调节的步长参数，c(k)＝e(k)e(k-1)×(x|第k行)(x|第k-1行)^t,

σ(k)＝(x|第k-1行)(x|第k-1行)^t+β(k-1)

则k时刻的学习速率

(3)计算待估计系统参数。

对于k时刻，w|第k行＝w|第k-1行+μ(k)e(k)(x|第k行)^*

则

8.求解线性方程组即可求解各通道非线性系统参数。

如图1所示，这是带有非线性传输特性的双通道tiadc模型示意图，在实现高速采样的模数转化时，输入信号分别以两通道输入，在每条通道受到不同的失真传输函数的影响，导致最终合并出输出信号产生了非线性失真。图2为低通信号采样的频谱示意图，在输入信号的频带外的频域中，只含有误差信号的信息d和s，为此，在该区域可对非线性误差信号的参数进行盲估计。

本发明采用的测试信号为高斯白噪声通过一低通滤波器所产生的信号，该低通滤波器为619阶的第一类线性相位fir滤波器，截止频率为0.79π，阻带幅度为-100db。因此，tiadc的输入信号满足低通信号的要求。下面以具有三阶非线性特性的tiadc为例，对本发明的的具体实施方式作详细的描述，其非线性特性为：对任意l＞3,并且

本发明把双通道tiadc的误差参数的系数按发明原理所述转换为参数s和d，并对此分别进行估计。用变步长nlms估计s参数的结构图如图3所示。这里f[n]是一个截止频率为0.8π，阻带幅度为-80db的63阶的第一类线性相位fir高通滤波器。变步长nlms估计结构是一个有l-1个权系数s2，s3...sl的自适应线性组合器，这是一个多输入系统。tiadc的各阶输出信号经过f[n]作用之后，可以理解为l-1个不同的信号源到达的瞬时输入，即ys²[n]、ys³[n].......ys^l[n]。而估计结构的期望信号则用tiadc的输出信号y[n]通过f[n]产生。

按照上述发明原理所述，为达到更好的收敛效果和避免剧烈震荡，学习速率偏移参数γ设置为0.0001，步长参数α为0.0003，以此对s2，s3...sl进行变步长nlms估计，盲估计的结果如图4所示，估计过程产生的均方误差如图5所示，可见s2收敛至-0.0009，s3收敛至0.0032，均方误差也随着迭代次数的增加快速降低。

相似地，用变步长nlms估计d参数的结构图如图6所示。所不同的是tiadc各阶的输出信号经过f[n]作用之前，还需通过一个(-1)ⁿ的乘法器，其学习速率偏移参数γ和步长参数α仍设为0.0001和0.0003。以此对d2，d3...dl进行变步长nlms估计，估计的结果如图7所示，均方误差如图8所示，可见d2收敛至-0.0019，d3收敛至0.0014。

通过求解线性方程组，结果保留小数点后3位，可解得

总的来说，对于低通输入信号，本发明提出了一种基于可变步长n-lms算法的tiadc非线性误差估计方法。从以上的实验结果可以看出该方法能够有效估计双通道tiadc的非线性误差参数。该方法鲁棒性强，简单易行，收敛速度快，能有效提高tiadc的性能。

相同或相似的标号对应相同或相似的部件；

附图中描述位置关系的用于仅用于示例性说明，不能理解为对本专利的限制；

显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。