混合修正加权比特翻转的LDPC译码算法的利记博彩app与工艺
本发明涉及数字信息传输技术领域的一种混合修正加权比特翻转的LDPC译码算法(MixedModifiedWeightedBit-Flipping,MM-WBF)技术,特别涉及一种混合修正加权比特翻转的LDPC译码算法。
背景技术:
随着社会经济的快速发展,个人通信的需求越来越高,不仅要求在“任何时间、任何地点与任何人”进行通话,而且要求通信技术“宽带化、实时化及多媒体化”;“编解码”技术作为通信技术中的重要组成部分,同样面临着更高的要求;Low-DensityParity-Check(LDPC)码是通过稀疏校验矩阵定义的线性码,最早在20世纪60年代由Gallager在其博士论文中提出;但限于当时的技术条件,无法实用化,因此一直被人们忽略;直到90年代,MacKay和Neal等人对LDPC码重新进行了研究,发现LDPC码具有十分优越的性能,迅速引起强烈反响和极大关注;目前LDPC码已广泛应用于深空通信、光纤通信、卫星数字视频和音频广播等领域;LDPC码已被下一代卫星数字视频广播标准DVB-S2采纳,并成为第四代通信系统(4G)纠错码方案强有力的竞争者。LDPC码的译码算法包括以下三大类:硬判决译码,软判决译码和混合译码。硬判决译码实现简单,解码速度快,但是性能较差,常见的硬判决译码算法有比特翻转(bit-flipping,BF)算法;软判决译码实现较为复杂,解码速度较慢,但性能最佳,常用的软判决译码算法有置信传播(beliefpropagation,BP)算法等;而混合译码结合了软判决译码和硬判决译码的特点,在硬判决译码的基础上,利用部分信道信息进行可靠度的计算;混合译码在解码性能、复杂度及解码速度三者间取得了较好的平衡,因此受到广泛关注,其代表算法包括加权比特翻转(weightedBF,WBF)系列算法。加权比特翻转系列算法的基本思路是在每次迭代中找到最有可能出错的比特进行纠正,然后重复迭代过程直至解码成功或者达到最大迭代次数;近年来提出的加权比特翻转算法主要有:modifiedweightedbit-flipping(M-WBF),lowcomplexityweightedbit-flipping(LC-WBF),reliabilityratiobasedweightedbit-flipping(RR-WBF),fastmodifiedweightedbit-flipping(FM-WBF),improvedmodifiedweightedbit-flipping(IM-WBF)等;相关专利有:低密度校验码的并行加权比特翻转解码方法(CN200710019237.4,有效),一种有限几何低密度奇偶校验码的译码方法(CN200710120057.5,有效),混合比特翻转和大数逻辑的LDPC译码方法(CN200910067809.5,在审)。然而,上述加权比特翻转系列算法的性能与软判决译码算法相比仍有较大差距,尤其对于非正则LDPC码。因此,迫切需要一种性能更佳,收敛更快的加权比特翻转算法。
技术实现要素:
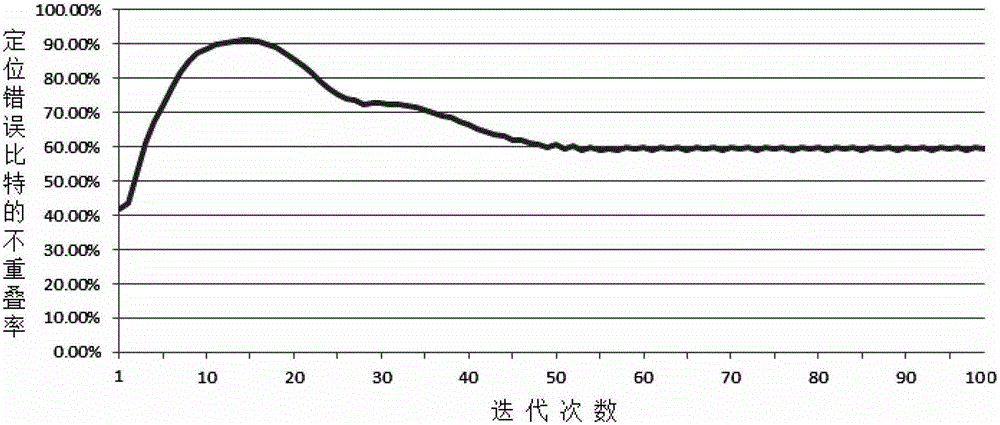
本发明的目的在于克服现有技术的缺点与不足,提供一种混合修正加权比特翻转的LDPC译码算法。该算法选取两种现有的加权比特翻转算法进行混合,但是较现有加权比特翻转算法的解码性能更佳,收敛速度更快。该算法基于现有的两种加权比特翻转算法在解码过程中对错误比特定位相异的特点,采用其中一种算法作为主算法,另外一种算法作为辅助算法进行混合构造而成。该算法在复杂度总体基本无变化的情况下,较现有的其他加权比特翻转算法提升了0.3~0.6dB的编码增益,解码速度提升近一倍。本发明的目的通过以下技术方案实现:混合修正加权比特翻转的LDPC译码算法,选取两种现有的加权比特翻转算法进行混合,所述主算法采用对于待解的码组现有加权比特翻转算法中性能最佳的算法,所述辅助算法选取性能次佳的算法,并设置最大迭代次数;解码过程中,解码器首先对接收到的码字进行硬判决,得到判决后的码字序列作为解码的输入信息(如附图1所示),此处所述主算法采用RR-WBF算法,所述辅助算法采用IM-WBF算法;所述RR-WBF的表达式为:所述IM-WBF算法的表达式为:其中,|yn|表示信道输出值的绝对值。sm表示校验矩阵的伴随式。α为数值且可调,n∈N(m)m=1,2,…,W。最大迭代次数(MaximumNumberofIterations)指在译码过程中允许迭代次数的最大值。当达到最大迭代次数时,不管是否成功译码,将中止译码过程,输出当前的译码结果。本发明的译码算法包括以下步骤:步骤1:解码器初始化,测算用于步骤3的相关参数,即用于计算主算法及辅助算法的判决标准En1、En2的相关参数;步骤2:通过计算校验矩阵的伴随式,得到当前输入的码字序列的校验结果。如果伴随式为全0,译码成功并结束;否则,进入步骤3。步骤3:根据步骤1的参数及步骤2的伴随式结果,计算主算法判决标准值En1以及辅助算法判决标准值En2。步骤4:根据主算法判决标准值En1得到此算法所认定的码字序列中最可能错误的比特位置p;根据辅助算法判决标准值En2得到此算法所认定的码字序列中最可能错误的比特位置q;步骤5:如果p≠q,且位置q对应的比特zq之前没有被主算法翻转过,那么可判定位置p对应的比特zp和位置q对应的比特zq都是错误比特,同时进行纠正;否则,只纠正zp;重复步骤2至步骤5,当成功解码或者达到最大迭代次数时,停止迭代,输出解码序列。需要强调的是,步骤5是在“p≠q”、“且位置q对应的比特zq之前没有被主算法纠正过”两个条件同时成立时,方可判定位置p和位置q对应的比特都是错误比特,同时进行纠正。主要原因是主算法具有比辅助算法更佳的解码性能,因此通过主算法判定的错误比特,其可靠性比通过辅助算法判定的错误比特更大。如果仅当p≠q就纠正zp和zq,则有可能出现zp纠错正确而zq纠错失败的情况,导致MM-WBF的解码性能被辅助算法拖累,而最终性能逊于主算法。因此,当p≠q时,需要确保位置q的比特本身并没有被主算法纠正过,才同时纠正两个比特;否则,只允许纠正zp,以确保MM-WBF的解码性能。所述校验矩阵H具有W行L列,Hmn表示校验矩阵第m行的第n个元素。所述步骤(2)中,计算所述校验矩阵的伴随式的方法为:m=1,2,…,W。所述步骤(4)中,所述把p定位为最可能错误的比特位置的方法为:所述把q定位为最可能错误的比特位置的方法为:其中,En1为主算法的判决标准值,En2为辅助算法的判决标准值。本发明的工作原理:由于主算法与辅助算法用于选取错误比特的判定标准不同(如图2所示),两种算法在每次迭代过程中选取的错误比特不尽相同(见图3、图4所示);因此,较其他加权比特翻转算法在每个迭代周期中翻转1个比特,MM-WBF在每个迭代周期中很有可能翻转2个比特,从而能够将解码速度提升将近一倍。大部分加权比特翻转算法解码失败的原因在于陷入错误比特判定失败的循环,也就是说,算法无法正确解码,只是不断地在错误比特中进行反复翻转。而MM-WBF采用两种用于寻找错误比特的判决标准,有助于打破错误的纠错循环,从而提升解码性能;例如,当主算法En1陷入错误的纠错循环时,辅助算法En2通过纠正另一个错误比特,可以帮助主算法打破错误的循环;反之亦然,当辅助算法En2陷入错误的纠错循环时,主算法En1通过纠正另一个错误比特,可以帮助辅助算法打破错误的循环。本发明相对于现有技术具有如下的优点及效果:(1)在总体复杂度变化不大的情况下,较现有的其他加权比特翻转算法提升了0.3~0.6dB的编码增益。(2)译码收敛速度较现有的其他加权比特翻转算法提升近一倍。(3)该发明的核心是加权比特翻转算法,与软判决译码算法比较,计算复杂度低,硬件实现方便。附图说明图1为本发明的工作流程图。图2为本发明的依据之一:几种现有加权比特翻转算法判决标准的公式构造单元对比。图3为本发明的依据之二:IM-WBF和RR-WBF定位错误比特的不重叠率的示意图。图4为本发明的依据之二:IM-WBF和LC-WBF定位错误比特的不重叠率的示意图。图5为本发明的仿真验证图:(1008,504)非正则LDPC码的误码率对比示意图。图6为本发明的仿真验证图:(1008,504)非正则LDPC码的平均迭代次数对比示意图。图7为本发明的仿真验证图:(2048,1018)非正则LDPC码的误码率对比示意图。图8为本发明的仿真验证图:(2048,1018)非正则LDPC码的平均迭代次数对比示意图。图9为本发明的仿真验证图:(4000,2000)正则LDPC码的误码率对比示意图。图10为本发明的仿真验证图:(4000,2000)正则LDPC码的平均迭代次数对比示意图。具体实施方式下面结合实施例及附图对本发明作进一步详细的描述,但本发明的实施方式不限于此。实施例本发明属于数字信息传输技术领域的一种混合修正加权比特翻转的LDPC译码算法(MixedModifiedWeightedBit-Flipping,MM-WBF),现对该算法的具体实施方式进行说明。如图1所示,是本发明算法对(L,K)LDPC码的具体实施方式,其中L表示码字长度,K表示信息比特长度。设定H=[Hmn]是LDPC码的校验矩阵,即由0和1组成的W行L列的矩阵,W≥L-K。N(m)={n:Hmn=1}表示参与校验节点m的所有比特节点,M(n)={m:Hmn=1}表示有比特节点n参与的所有校验节点。N(m)\n表示除n以外参与校验节点m的所有其他比特节点,M(n)\m表示除m以外比特节点n参与的所有其他校验节点。设LDPC码字c={c1,c2,…,cL}经过xn=2cn-1调制后,变成x={x1,x2,…,xL},信道为高斯白噪声(AWGN)信道,接收到的码字序列为x+w=y={y1,y2,…,yL},其中yn=xn+wn,wn为独立的高斯白噪声变量。译码后的比特序列为z={z1,z2,…,zL}。根据现有加权比特翻转算法,我们选取RR-WBF作为主算法,IM-WBF作为辅助算法对MM-WBF的具体实施方式进行说明:步骤1:如图1中步骤1所示,解码器初始化,测算用于计算主算法及辅助算法判决标准En1及En2的相关参数。因RR-WBF为主算法,IM-WBF为辅助算法,因此根据其判决标准的公式,需计算:n∈N(m)m=1,2,…,W,步骤2:如图1中步骤2所示,计算当前码字的伴随式得到当前输入的码字序列的校验结果。如果伴随式为全0,译码成功并结束,否则,进入步骤3。步骤3:如图1中步骤3所示,计算主算法及辅助算法的判决标准En1及En2。(1)主算法RR-WBF为:(2)辅助算法IM-WBF为:步骤4:如图1中步骤4所示,根据En1中的最大值定位最可能错误的比特位置p,根据En2中最大值定位最可能错误的比特位置q;步骤5:如果p≠q,且位置q对应的比特zq之前没有被主算法纠正过,那么同时纠正比特zp和zq;否则,只纠正zp;重复步骤2至步骤5,当成功解码或者达到最大迭代次数时,停止迭代,输出解码序列。由于主算法与辅助算法用于选取错误比特的判定标准不同(如图2所示),两种算法在每次迭代过程中选取的错误比特不尽相同;如图3和图4所示,是分别为对于(2048,1018)非正则LDPC码,IM-WBF与RR-WBF算法定位错误比特的不重叠率以及IM-WBF与LC-WBF算法定位错误比特的不重叠率。因此,较单个加权比特翻转算法在每个迭代周期中翻转1个比特,MM-WBF在每个迭代周期中很有可能翻转2个比特,从而能够将解码速度提升将近一倍。同时,大部分加权比特翻转算法解码失败的原因在于陷入错误比特判定失败的循环,也就是说,算法无法正确解码,只是不断地在错误比特中进行反复翻转。而MM-WBF采用两种用于寻找错误比特的判决标准,有助于打破错误的纠错循环,从而提升解码性能;例如,当主算法En1陷入错误的纠错循环时,辅助算法En2通过纠正另一个错误比特,可以帮助主算法打破错误的循环;反之亦然,当辅助算法En2陷入错误的纠错循环时,主算法En1通过纠正另一个错误比特,可以帮助辅助算法打破错误的循环。在高斯白噪声(AWGN)信道及BPSK调制的情况下,以(1008,504)非正则码、(2048,1018)非正则码以及(4000,2000)正则码为例,对比MM-WBF与LC-WBF、RR-WBF、IM-WBF等加权比特翻转算法的性能及平均迭代次数。(1)如图5和图6所示:对于(1008,504)非正则码,在误码率为10-4附近,MM-WBF相比RR-WBF有0.4dB增益,相比IM-WBF有0.6dB增益,相比LC-WBF的增益更大。而MM-WBF的平均迭代次数约为RR-WBF及IM-WBF的50%~60%,仅为LC-WBF的1/3,即迭代收敛速度至少增加了将近一倍;(2)如图7和图8所示:对于(2048,1018)非正则码,在误码率为10-4附近,MM-WBF相比RR-WBF及IM-WBF有0.3dB增益,相比LC-WBF的增益更大。而MM-WBF的平均迭代次数约为RR-WBF及IM-WBF的50%~60%,仅为LC-WBF的1/3,即迭代收敛速度至少增加了将近一倍;(3)如图9和图10所示:对于(4000,2000)正则码,在误码率为10-4附近,MM-WBF相比RR-WBF及IM-WBF有0.3dB增益,相比LC-WBF的增益更大。而MM-WBF的平均迭代次数约为RR-WBF、IM-WBF及LC-WBF的50%~60%,即迭代收敛速度增加了将近一倍;由于MM-WBF基于两种加权比特翻转算法进行混合构造,因此在每个迭代周期中,MM-WBF的计算复杂度是其他加权比特翻转算法的两倍。但是由于MM-WBF的平均迭代次数约为其他加权比特翻转算法的50%~60%。因此总的复杂度变化不大。且其主算法及辅助算法均源于现有加权比特翻转算法,与软判决译码算法比较,计算复杂度低,硬件实现方便,实现简单。上述实施例为本发明较佳的实施方式,但本发明的实施方式并不受上述实施例的限制,其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化,均应为等效的置换方式,都包含在本发明的保护范围之内。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1