一种多域电力系统负荷频率控制方法与流程
本发明涉及一种电力系统负荷频率控制方法,尤其是涉及一种多域电力系统负荷频率控制方法。
背景技术:
频率是衡量电力系统安全稳定运行的重要指标之一。为保证电力系统电能的质量,保持系统有功平衡是十分必要的。化石能源的日益枯竭,全球环境的迅速恶化,使得可再生能源得到大力发展,如风能、太阳能、潮汐能等。风能作为一种清洁可再生能源在能源结构中占据着重要的地位。近年来,风能渗透率在世界范围内得到了快速的增长。然而,风能的波动性和不确定性使得系统频率波动较大。因此,系统频率不稳定是一个亟需解决的问题。
目前,电力系统频率调节的方式主要有三种:一是通过配置储能维持系统功率平衡;二是通过控制传统发电机组来维持频率稳定;三是新能源发电参与电力系统频率调节。第三种调频方式目前正处于研究阶段,尚未得到广泛的应用,因此本发明只研究前两种调频手段。自动发电控制(agc)是实现电网有功平衡和频率稳定的主要手段,但是agc响应时间长,不能准确跟踪控制指令。此外,随着风能渗透率的不断增加,单独依靠传统发电机组平衡系统的有功需求是十分困难的。
随着储能技术的发展和价格的降低,越来越多的储能系统接入电网运行。储能系统有准确而快速的响应能力,能够对系统频率偏差迅速做出反应从而抑制系统频率波动。不同的储能装置有着不同的特点,例如,电池储能系统响应速度慢、能量密度高、使用寿命短;相反,超级电容响应速度快、功率密度高、能量密度低,使用寿命长。因此,当单一的储能类型不能满足系统安全稳定运行的需求时,混合储能系统得到广泛的应用。超级电容与电池储能系统配合使用可更好地发挥各自的优点。
尽管混合储能系统在合理的控制下能够使电力系统稳定运行,但是随着风能渗透率的提高,如果仅利用储能技术调节频率,将增加电网建设的成本。因此,国内外学者将先进控制理论应用到负荷频率控制lfc中,例如pi控制、模糊控制、神经网络、自适应控制和滑模(sm)控制。其中滑模控制算法对外部干扰和参数不确定性具有不敏感性,可有效提高了电力系统的鲁棒性。因此针对传统发电机组设计了滑模控制器。
技术实现要素:
本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种多域电力系统负荷频率控制方法,以含风能和混合储能系统的互联电网为研究对象,根据系统调频区间,协调控制混合储能系统和传统发电机组,并针对传统发电机设计了滑模负荷频率控制器,控制策略可有效减小系统频率偏差,提高电力系统稳定性,减小电网建设的成本。
本发明的目的可以通过以下技术方案来实现:
一种多域电力系统负荷频率控制方法,所述的电力系统包括多个通过联络线互联的区域,各区域中包括传统发电机、超级电容器、电池储能系统和风力发电机,所述的方法包括:根据区域控制偏差ace的值所处的控制区间,令频率调节装置的输出功率发生相应调整,使系统频率偏差保持在正常范围内。
所述的区域控制偏差ace计算式为:ace=δpij+bδf,其中,δf是系统频率偏差(系统频率实际值和额定值的差),b是区域频率偏移系数,δpij是联络线功率偏差。
所述的控制区间定义包括:
死区,|ace|≤aced.set,其中aced.set是死区中ace的最大值;;
正常调节区,aced.set<|ace|≤acen.set,其中acen.set是正常调节区中ace的最大值;
辅助调节区,acen.set<|ace|≤acee.set,其中acee.set是紧急调节区的门槛值;
紧急调节区,|ace|>acee.set。
当ace处于死区时,各频率调节装置不作回应;当ace处于正常调节区时,仅传统发电机调整输出的有功功率;当ace处于辅助调节区时,仅传统发电机和超级电容器调整输出的有功功率或无功功率;当ace处于紧急调节区时,所有的频率调节装置均参与相应,产生最大功率以使ace恢复正常。
所述的aced.set,acen.set和acee.set通过调度部门对历史数据的分析和经验估计获得。
所述的方法还包括:对传统发电机采用滑模控制器进行频率控制。
根据积分型滑模面s(t)=cx(t)-∫c(a-bk)x(τ)dτ设计滑模控制器u(t),所述的滑模控制器u(t)表达式为:u(t)=-kx(t)-(cb)-1[cw+ns(t)+msgns(t)],
其中,x(t)为系统状态向量,a为系统矩阵,b为输入矩阵,c和k是具有适当维数的常数矩阵,矩阵k满足λ(a-bk)<0,矩阵c使得cb可逆,w为系统集结不确定项的积分,n和m是正数,sgn*是符号函数,
所述的状态模型如下:
其中x(t)=[δf1δpm1δpv1δe1δp12δf2δpm2δpv2δe2]t,
u(t)=[u1u2]t,δpl(t)=[δpl1δpl2]t
其中,下标1表示区域1的参数;下标2表示区域2的参数,两区域通过联络线互联;kp1,kp2为电力系统增益;tp1,tp2为电力系统时间常数;tch1,tch2为汽轮机时间常数;tg1,tg2为调速器的惯性时间常数;r1,r2为调速器速度调节系数;ke1,ke2为积分控制增益;b1,b2为系统频率偏差系数;t12为联络线功率同步系数;u1,u2为设计的滑模负荷频率控制器;δf1,δf2为区域频率偏差;δpm1,δpm2为火电机组的响应功率;δpv1,δpv2为调节阀位置增量;δe1,δe2为频率偏差积分控制器增量;δp12为联络线功率偏差;δpl1,δpl2为负荷扰动;x(t)为系统状态向量;a为系统矩阵;b为输入矩阵;f为干扰系数矩阵。
与现有技术相比,本发明具有以下优点:
(1)将电力系统调频区间划分,根据ace所属区间采取对应的控制策略,有效减小了系统频率偏差,提高电力系统稳定性,减小了电网建设的成本。
(2)在控制区间的划定中,门槛值的选择主要是根据调度部门的历史数据分析和经验估计而定的。在不同的控制区间内,控制不同的调频装置输出功率,可充分利用各种调频装置的优点,避免其他装置频繁动作,从而提高使用寿命。
(3)针对传统发电机设计了滑模负荷频率控制器,可提高对传统火电机组的控制精度,增强电力系统的鲁棒性。
(4)多种类型的储能系统参与电力系统的频率调节,可充分利用它们各自的优点,达到优势互补的效果。
附图说明
图1为本实施例互联电力系统框图;
图2为本实施例电池储能系统传递函数;
图3为本实施例超级电容传递函数;
图4为本实施例风力发电机系统配置;
图5为本实施例ace分区示意图;
图6为本实施例协调控制流程图;
图7为本实施例两域系统仿真结构图;
图8为本实施例阶跃负荷扰动;
图9为本实施例含阶跃负荷扰动下的仿真结果,其中图9(a)为案例1中系统频率偏差的波形,图9(b)为案例1中超级电容的输出功率,图9(c)为案例1中电池储能系统的输出功率;
图10为本实施例随机负荷扰动;
图11为本实施例含随机负荷扰动下的仿真结果,其中图11(a)为案例2中系统频率偏差的波形,图11(b)为案例2中超级电容的输出功率,图11(c)为案例2中电池储能系统的输出功率;
图12为本实施例风机输出功率;
图13为本实施例含风机和随机扰动下的仿真结果,其中图13(a)为案例3中系统频率偏差的波形,图13(b)为案例3中超级电容的输出功率,图13(c)为案例3中电池储能系统的输出功率。
具体实施方式
下面结合附图和具体实施例对本发明进行详细说明。本实施例以本发明技术方案为前提进行实施,给出了详细的实施方式和具体的操作过程,但本发明的保护范围不限于下述的实施例。
实施例
本实施例多元互补电力系统拓扑结构图如图1所示。在频域内有功平衡方程为
pmi+pgwi+pbessi+puci-ptie-ij=pli(1)
其中,i=1,2,j=1,2(i≠j),pmi是传统发电机输出功率;pgwi是风机输出功率,pbessi是电池储能系统的输出功率;puci是超级电容的输出功率;ptie-ij是联络线传输功率;pli是区域有功负荷。
虽然电力系统是非线性动态系统,但是由于负荷在稳定运行点附近的变化范围是很小的,在研究负荷频率控制问题时电力系统模型是可以进行线性化的。
1)传统发电机模型
大部分的传统发电机组是火力发电机组,它们是系统频率调节的主要方式,可提供稳定而可靠的有功功率。传统发电机模型如下所示
其中,i=1,2,j=1,2(i≠j),δfi(t)是频率偏差;δpmi(t)是传统发电机输出功率增量;δpvi(t)是传统发电机调节阀位置增量;δei(t)是积分控制增量;δpij(t)是联络线功率偏差;ui(t)是滑模控制器输出的控制信号;δpli(t)是系统负荷扰动;tij是联络点增益;tpi是电力系统时间常数;tchi是发电机时间常数;tgi是调速器时间常数;kpi是系统增益;kei是积分控制增益;ri是调速器速度调节系数;bi是区域频率偏移系数。
2)电池储能系统数学模型
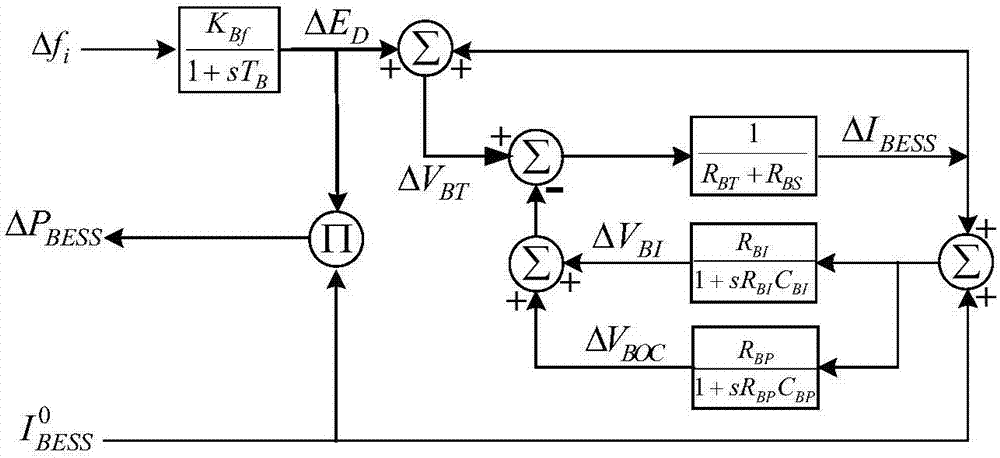
电池储能系统采用外部特性等效电路模型,其结构框图如图2所示。数学描述如下
其中,δed是储能系统端电压偏差、δvbt是内阻端电压增量,tb是电池时间常数;kbf是频率偏差控制增益;δvbi是过电压增量;δvboc是电池开路电压增量;rbt是连接电阻;rbs是电池内阻;rbi是过电压电阻;cbi是过电压电容;rbp是自放电电阻;cbp是电池电容;
3)超级电容数学模型
超级电容通常等效为电容和电阻并联电路。当考虑电容初始电压时,引入了电压反馈回路以维持电容电压稳定。超级电容传递函数如图3所示。数学描述如下
δpuc=(edo+δed)δid(14)
其中,δid、δed和δpuc分别是超级电容电流增量、电压增量和输出功率增量;δfi是系统频率偏差;tc是超级电容时间常数;kcf是控制增益;kvd电压反馈增益;r和c是超级电容等效电阻和电容;ed0是初始电容电压。
4)风机数学模型
鼠笼型感应发电机由于它的结构简单和可靠性高得到了广泛的应用。风机系统配置图如图4所示。风机输出的机械功率pwi的表达式如下
其中,vw是风速;ρ是空气密度;cp(λ,β)是风能利用系数;β是桨距角;r是叶片半径,叶尖速比λ为
其中,r是叶片半径;ω是涡轮叶片角速度;ω可由下面公式得出
其中,j是系统的等效总转动惯量,pwi是风机输出的机械功率,pgi是鼠笼型发电机输出的功率。当ω大于等于转子同步角速度ω0时,鼠笼发电机的输出功率pg为
其中,v是相电压r1是定子电阻;r2是转子电阻;x1是定子电抗;x2是转子电抗;
协调控制策略
1)调频区间划分
在互联电力系统中,ace是衡量系统稳定性的重要指标,它综合反映系统的频率和联络线功率。在实际agc系统中,ace的值可分为四个控制区间,分别为死区、正常调节区、辅助调节区和紧急调节区。ace的四个区间如图5所示。
根据图5可得
(1)ace≤|aced|,称为死区;
(2)|aced|≤ace≤|acea|,称为正常调节区;
(3)|acea|≤ace≤|acee|,称为辅助调节区或警戒调节区;
(4)ace≥|acee|,称为紧急调节区。
2)各调频区间的控制策略
调度中心实时监测电力系统运行状态,并可快速获得系统的安全水平和ace的值。然后通过一个复杂的算法来调整可利用调频装置的输出功率。在电力系统中,发电量和负荷必须时刻保持平衡,这种平衡可以通过测量频率偏差来测量。如果这种平衡被打破,调度中心根据经济和安全调整各频率调节装置的输出功率。详细的协调策略的细节如下:
(1)死区
为了避免由小的频率波动而引起的调速系统的频繁动作,在机组的一次调频控制回路中设置了调频死区。在死区范围内,ace的值和频率偏差非常小,系统频率基本保持在额定值附近。因此,频率调节资源可不作任何回应。
(2)正常调节区
当电力系统发生小负荷扰动时,在这种情况下通常认为ace的值是小的。系统仍处于正常运行状态。ace的值满足下列条件
aced.set<|ace|=|δpij+bδf|≤acen.set(19)
其中,δf是测得的系统频率偏差;b是区域频率偏移系数;δpij是联络线功率偏差;aced.set是死区中ace的最大值;acen.set是正常调节区中ace的最大值。
这种状态下的有功功率要求相对较小,以经济性为最大目标。因此,只有传统的发电机调整输出的有功功率,以减小系统频率偏差。同时,延长了超电容器和电池储能系统的使用寿命。
(3)辅助调节区
在辅助调节区,系统处于异常运行状态时,但频率偏差仍在允许范围内。ace的值满足以下约束:
acen.set<|ace|≤acee.set(20)
其中,acee.set是紧急调节区ace的门槛值。
在这种情况下,系统频率偏差和联络线功率偏差大,系统运行状态异常。如果没有迅速补偿有功功率的缺额,系统状态将进入紧急状态。因此,寻找一种可靠、经济的解决方案是十分必要的。此时,引入了超级电容器,可以在短时间内提供较大输入或输出功率。然而,传统发电机具有较长的响应时间,它可以提供稳定的有功功率。超级电容器与传统发电机相结合可有效降低频率偏差。同时,避免了电池储能系统的使用,防止其过充或过放电从而延长了寿命。
(4)紧急调节区
在紧急调节区,系统频率偏差较大,系统运行状态处于紧急状态。ace的值满足以下约束条件:
|ace|>acee.set(21)
在这种情况下,需要很大的响应功率,使电力系统恢复正常状态。在这个时刻,系统的安全运行是最为关键的。如果不能立即处理,将导致严重后果。因此,各种频率调节装置应共同参与,产生最大功率来平衡有功功率。电池储能系统和超级电容器将立即参与响应,然后传统发电机组随后做出响应。在一定程度上,它们的优点得到充分的互补的。针对传统发电机设计滑模负荷频率控制器能够降低储能系统的投资,提高低电网运行的经济性。
根据以上的分析,提出的控制策略流程图如图6所示。通过对调度部门对历史数据进行分析和经验估计,可以得出aced.set,acen.set和acee.set的近似值。
针对传统机组设计滑模控制器
滑模控制算法具有很强的鲁棒性,特别是当系统的状态移动到滑模面,对系统外部干扰具有不敏感性。
(1)滑模面设计
根据等式(2)-(6)得如下向量模型
其中,x(t)=[δf1δpm1δpv1δe1δp12δf2δpm2δpv2δe2]t,
u(t)=[u1u2]t,δpl(t)=[δpl1δpl2]t,
其中,下标1表示区域1的参数;下标2表示区域2的参数;kp1,kp2为电力系统增益;tp1,tp2为电力系统时间常数;tch1,tch2为汽轮机时间常数;tg1,tg2为调速器的惯性时间常数;r1,r2为调速器速度调节系数;ke1,ke2为积分控制增益;b1,b2为系统频率偏差系数;t12为联络线功率同步系数;u1,u2为设计的滑模负荷频率控制器;δf1,δf2为区域频率偏差;δpm1,δpm2为火电机组的响应功率;δpv1,δpv2为调节阀位置增量;δe1,δe2为频率偏差积分控制器增量;δp12为联络线功率偏差;δpl1,δpl2为负荷扰动;x(t)为系统状态向量;a为系统矩阵;b为输入矩阵;f为干扰系数矩阵。
在实际电力系统中,稳定运行点随着不断变化的负载和风力发电机组的输出功率而改变,从而导致系统参数的不确定性。因此,互联系统状态方程可重新定义为(22)
定义w(t)=δax(t)+δbu(t)+(f+δf)δpl(t)为集结不确定项,(22)变为
为设计控制器,做出如下假设:
假设1:(ai,bi)完全可控;
假设2:系统不确定项是非匹配的,即rank(bi,gi)≠rank(bi);
假设3:集结不确定项是有界的,即||w||<ξ,其中||.||是矩阵范数,ξ是正数。
本发明采用以下积分型滑模面
s(t)=cx(t)-∫c(a-bk)x(τ)dτ(24)
其中,c和k是具有适当维数的常数矩阵,矩阵k满足λ(a-bk)<0,矩阵c使得cb可逆。基于lyapunov稳定性分析,系统在滑模面上是稳定的。
(2)控制器设计
趋近律可提高系统到达阶段的动态品质,本发明中,采用以下等式趋近律
其中,n和m是正数,sgn*是符号函数。
由公式(24)和(25)可得
解得滑模控制器为
u(t)=-kx(t)-(cb)-1[cw+ns(t)+msgns(t)](27)
以此可知,系统满足到达条件
仿真分析
(1)仿真模型和参数
为了验证所提出的控制策略的有效性,在matlab/simulink平台下进行了仿真研究。两域互联系统模型如图7所示。电力系统的模型参数如表1所示。
表1:系统仿真参数
仿真案例
(2)案例1
阶跃负荷扰动如图8所示。ace的值处于正常调频区域内,系统运行状态正常。因此,传统发电机在滑模负荷频率控制器作用下通过调整其输出功率单独进行频率调节。通过与配有混和储能系统的pilfc比较,对提出控制策略的有效性进行了验证。
通过图9的仿真结果可知,在提出的控制策略下系统最大频率偏差是0.085hz,而配有混和储能系统的pilfc中最大频率偏差是0.11hz。因此,所提出的控制方法有效减小频率偏差而且响应时间较短。此外,在提出的控制策略下混合储能系统的有功功率输出是零。但在pilfc中,超级电容器和电池储能系统的输出功率分别为0.16pu和0.048pu。因此,所提出的协调控制策略能够避免混合储能系统频繁动作,延长了超级电容器和电池储能系统的寿命。
(3)案例2
本案例中,当t=5s时图10所示的随机负荷扰动加入到互联系统的两个区域中。ace的值在辅助调节区内,仿真结果如图11。
图11中,所提出的方法,smlfc和配置混合储能的pilfc的最大频率偏差分别为0.188hz,0.28hz和0.34hz。显然,与其他两种控制方法相比,提出的方法响应速度更快,具有更小的超调量。在smlfc中,系统最大频率偏差大于±0.2hz。因此,超级电容立即动作并吸收功率是很有必要的。之后,传统发电机在滑模负荷频率控制器作用下调整其输出功率。超级电容器与传统发电机的结合可以有效地提高系统的电能质量。此外,所提出的方法比配置混合储能的pilfc相比,避免超级电容器过充过放,延长了电池储能系统的寿命,这在一定程度上降低了系统稳定运行的投资
(4)案例3
在这种情况下,如图12所示的风力发电机组输出功率和随机负荷扰动同时加入互联系统中。ace处于急救调节区,系统频率偏差和超级电容与电池储能系统输出功率的仿真结果如图13所示。
在这种情况下,频率偏差和ace的值是较大的。为了保持系统的正常工作,所有的频率调节装置对频率偏差做出响应。超级电容和电池储能系统立即动作,其最大输出功率分别0.4pu和0.1pu,它比配置混合储能的pilfc中超级电容和电池储能系统的输出功率小。然后,传统发电机组在滑模负荷频率控制器作用下做出响应。当系统恢复正常运行状态时,电池储能系统会自动退出服务。但最重要的是,在提出方法的控制下系统的最大频率偏差接近0.2hz,但smlfc和配置混合储能的pilfc都超过0.32hz。提出的协调控制策略可以有效地提高系统的稳定性和电力运行的经济性。
- 还没有人留言评论。精彩留言会获得点赞!