基于市场利益的能效电厂优化配置与厂网协调规划方法与流程

本发明涉及电力市场规划领域，尤其是涉及一种基于市场利益的基于市场利益的能效电厂优化配置与厂网协调规划方法。

背景技术：

在电力系统中，通常把超过系统安全性限制的状态称为输电阻塞，这些安全性限制包括系统正常运行状态和非正常运行状态下的各种约束，如输电线路或变压器有功潮流热容量限制，节点电压限制，系统稳定限制等。为消除阻塞,应采取一系列的技术、经济措施，使系统运行于一定的安全和可靠性水平内，维持电力市场的有效运行，这一过程称为阻塞管理。

在垄断的体制下，系统调度、各发电厂和输电网同属一个经济实体，阻塞管理只需由调度员向各个电厂发出调度指令，根据需要调节机组出力，同时采取其它调度手段，如断开过负荷线路、调节变压器抽头或移相器、投入无功补偿设备、停止供应可中断负荷等，直至电力系统运行在安全性限制之内。但是在电力市场环境下，输电网和发电厂是独立的各具经济利益的实体，负责系统运行的独立系统调度员，必须平等对待各个市场成员，在社会效益最大化或购电成本最小化等目标下寻求合理的阻塞管理方法，并准确计算阻塞成本，为网络规划提供经济信号，促进系统在长期内稳定、健康地发展同时应将阻塞成本分摊至引起阻塞的市场参与者，为系统短期运行提供激励。

随着输电网络的开放，双边交易的参与者及交易电量迅速增多。在这种趋势下，如何有效地缓解阻塞并实现阻塞成本的快速分配成为电力市场研究的重要内容之一。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种有效地缓解阻塞、实现阻塞成本的快速分配、方法简单、实用性强的基于市场利益的能效电厂优化配置与厂网协调规划方法。

本发明的目的可以通过以下技术方案来实现：

一种基于市场利益的能效电厂优化配置与厂网协调规划方法，包括以下步骤：

1)根据灵敏度计算双边交易分摊的阻塞成本；

2)对基于市场利益的含能效电厂的厂网协调规划构建三层规划模型；

3)采对三层规划模型进行求解，获取电厂优化配置与厂网协调规划最优方案，并对方案进行连通性校验，确保最优方案不存在孤岛网架。

所述的步骤1)中，双边交易分摊的阻塞成本f的表达式为：

f＝ct·a^t·diag(b)/(a^tb)·diag(c)·d·diag(e)

其中，diag(·)表示以矩阵元素为对角元的对角矩阵，a为系统阻塞成本对阻塞线路功率的灵敏度，b为阻塞线路过负荷量，c为以阻塞线路功率倒数为元素的矩阵，d为阻塞线路功率对双边交易功率的灵敏度，e为实际的双边交易功率，ct为全网阻塞成本。

所述的步骤2)具体包括以下步骤：

21)以阻塞成本和投资成本之和最小作为目标函数构建上层规划模型；

22)以投资成本最小为目标函数建立中层规划模型，投资成本包括输电线路投资成本、常规电厂投资成本、epp投资成本以及切负荷惩罚费用；

23)以电厂的投资成本最小为目标函数建立下层规划模型，电厂投资成本包括新建常规电厂建设成本、新建能效电厂建设成本及运行维修成本。

所述的步骤21)中，上层规划模型的目标函数为：

min{f1+ct,1,f2+ct,2,...,fh+ct,h,...,fh+ct,h}

其中，f1、f2…fh...fh分别为第1、2…h…h种情形的各双边交易的分摊结果，ct,1、ct,2…ct,h、ct,h分别为第1、2…h…h种情形的全网阻塞成本，h为基于下层电源规划结果的新增电源节点配置情形种类总数，t为阶段总数，y为第t阶段包含的年数，为第i个发电机增投标报价，为第i个发电机第t阶段第y年第h种情形下的增发出力，为第j个发电机减投标报价，为第i个发电机第t阶段第y年第h种情形下的减发出力，th为年最大运行小时数；

所述的步骤21)中，上层规划模型的约束条件为：

其中，为第t阶段第y年第h种情形下的发电功率向量，为第t阶段第y年第h种情形下的负荷功率向量，为第t阶段第y年第h种情形下的系统节点导纳矩阵，为第t阶段第y年第h种情形下的电压相角向量，分别为第i个发电机增投标功率的下限和上限，为发电机减投标功率的下限和上限，分别为第t阶段发电机的功率下限向量和上限向量，为第t阶段第y年第h种情形下线路ij的传输功率，为第t阶段第h种情形下线路ij的最大传输功率。

所述的步骤22)中，中层规划模型的目标函数为：

其中，fh为第h种情形的中层目标值，r为贴现率，1/(1+r)^(t-1)y为资金的折算系数，ω为节点的集合，为第t阶段节点i到j的输电线路单位投资费用，lij为节点i到j之间输电线路的长度，为第h种情形下第t阶段节点i到j之间新建输电线路回数，g^t为电厂的投资成本，为第t阶段新建常规电厂投资成本，为第t阶段新建能效电厂投资成本，为第t阶段常规电厂的运行维修费用，为第h种情形下第t阶段n、n-1网络安全下的切负荷惩罚费用之和，为第h种情形下第t阶段正常运行状态下节点i的切负荷量，为第h种情形下第t阶段第s条线路断开的n-1运行状态下节点i的切负荷量，a、b为正常状态下的切负荷惩罚系数和n-1状态下的切负荷惩罚系数，i为节点数，s为线路回路数，y为第t阶段包含的年数。

所述的步骤22)中，中层规划模型的约束条件包括正常运行状态下潮流约束、线路有功潮流约束、n-1运行状态下潮流约束、线路有功潮流约束以及输电线路约束。

所述的步骤23)中，下层规划模型的目标函数为：

其中，g^t为电厂的投资成本，为第t阶段常规电厂的建设成本，为第t阶段能效电厂的建设成本，为第t阶段电厂的运行维修费用，m为常规电厂机组类型数，cg,m为新建常规发电机组类型为m的单位容量投资成本，pg,m为m型常规机组的容量，为第t阶段新建m型常规机组的台数，k为能效电厂机组类型数，ce,k为新建能效电厂类型为k的单位容量投资成本，pe,k为k型能效电厂的容量，为第t阶段新建k型能效电厂的台数，n为第t阶段包含所选择的待建常规电厂的常规机组数目，y为第t阶段包含的年数，为第t阶段第n个常规电厂机组的容量，iom&e,n为第n个常规电厂机组的单位运行维修费用，为第t阶段第n个常规电厂机组第y年的运行小时数，l为第t阶段包含所选择的待建能效电厂的能效电厂数目，为第t阶段第l个能效电厂机组的容量，iom,l为第l个能效电厂的单位运行费用，为第t阶段第l个能效电厂机组第y年的运行小时数。

所述的下层规划模型的约束条件包括：

机组备用容量约束、电量约束、系统中能效电厂的容量约束、常规电厂运行时间约束、能效电厂运行时间约束、新建常规电厂机组台数约束、新建能效电厂机组台数约束。

所述的步骤3)中，采用自适应遗传算法对上层决策变量进行求解，并且采用原始-对偶内点法对中层和下层进行快速求解。

与现有技术相比，本发明具有以下优点：

本发明中充分考虑在随着输电网络的开放，双边交易的参与者及交易电量迅速增多的趋势下，有效地缓解阻塞并实现阻塞成本的快速分配的重要性，本发明基于市场利益以能效电厂优化配置与厂网协调规划问题为出发点，通过建立模型和有效算法计算，得出最优规划方案具有方法简单、实用性强的优点。

附图说明

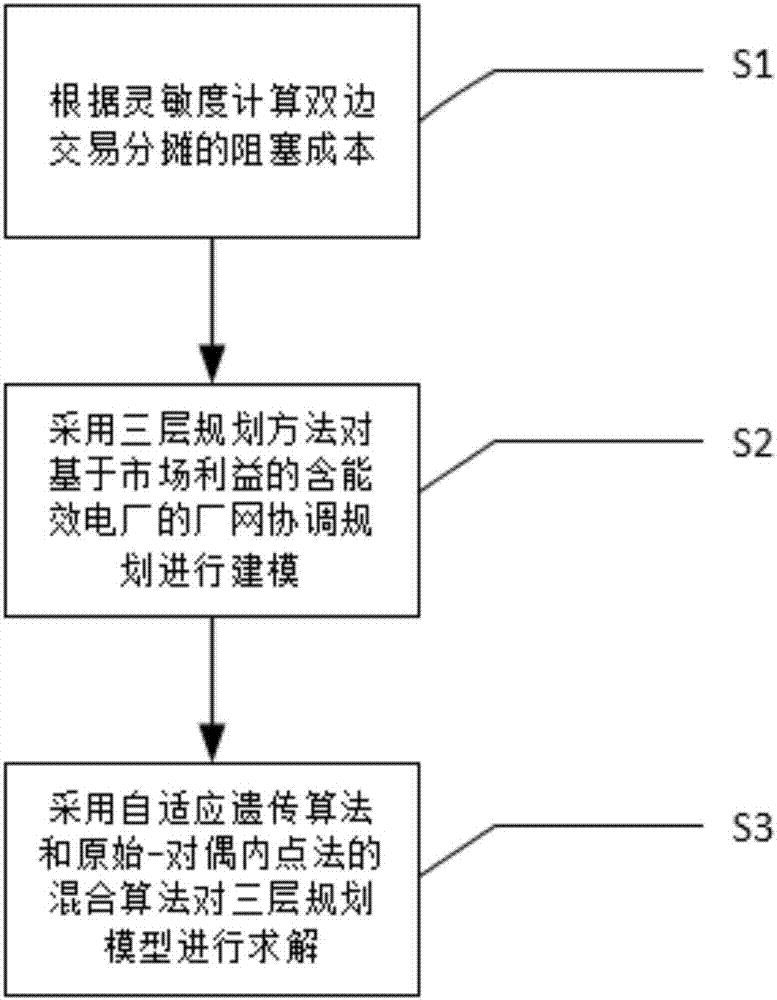
图1为本发明的发明流程图。

图2为本发明混合算法求解厂网协调规划流程图。

图3为实施例的ieee-rts24系统网络结构图。

图4市场利益下不考虑epp的厂网协调规划阶段一规划方案。

图5市场利益下不考虑epp的厂网协调规划阶段二规划方案。

图6市场利益下不考虑epp的厂网协调规划阶段三规划方案。

图7市场利益下考虑epp的厂网协调规划阶段一规划方案。

图8市场利益下考虑epp的厂网协调规划阶段二规划方案。

图9市场利益下考虑epp的厂网协调规划阶段三规划方案。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。

实施例

如图1所示，本发明提供一种基于市场利益的基于市场利益的能效电厂优化配置与厂网协调规划方法，包括以下步骤：

s1根据灵敏度计算双边交易分摊的阻塞成本，步骤s1中根据灵敏度计算双边交易分摊的阻塞成本，其具体步骤为：

步骤s11：生成以矩阵形式表达的双边交易分摊的阻塞成本，其中各阻塞线路的阻塞成本cij由下式确定：

式中，ct为全网阻塞成本；分数项表示线路i-j上单位功率所引起的阻塞成本，δpij为线路i-j的过负荷量。

从m点到n点的双边交易在阻塞线路i-j中分摊的阻塞成本为：

式中，pij为线路i-j的功率，pij,mn为阻塞线路i-j中由m点到n点的双边交易引起的功率，这一项可以通过下式来计算：

式中，表示在m点注入单位功率从n点流出单位功率时线路i-j中的功率变化量；tmn为双边交易实际交易功率。

从m点到n点的双边交易在全部阻塞线路中所分摊的阻塞成本为：

变形后可得：

式中，表示线路i-j单位功率所引起的阻塞成本；表示单位双边交易在线路i-j中引起的功率变化量；二者之积表示单位交易功率所引起的阻塞成本。δpij/pij是一个系数，表示阻塞成本应由线路中过负荷的部分承担，而不是由全部的功率承担。

假设系统在某时段存在t个双边交易，l条线路发生阻塞。各线路的首末节点分别用i、j表示，各双边交易的功率注入点和接收点分别用m、n表示。那么，对于这个时段产生的阻塞成本，各双边交易的分摊结果可用矩阵表示为：

f＝a^t·diag(b)·diag(c)·d·diag(e)

式中各矩阵分别为：

其中，diag(·)表示以矩阵元素为对角元的对角矩阵。以上各矩阵中，矩阵a为系统阻塞成本对阻塞线路功率的灵敏度，b为阻塞线路过负荷量；c为以阻塞线路功率倒数为元素的矩阵；d为阻塞线路功率对双边交易功率的灵敏度；e为实际的双边交易功率；f为双边交易分摊的阻塞成本。其中，矩阵e可以根据计算条件确定，b、c可以根据潮流计算获得。

步骤s12：计算灵敏度矩阵，其中阻塞线路最终分摊的成本为：

式中，cij为各阻塞线路的阻塞成本；c′ij为线路l最终分摊的阻塞成本。用矩阵表示的各双边交易的分摊结果可修改为：

f＝ct·a^t·diag(b)/(a^tb)·diag(c)·d·diag(e)

矩阵d为线路功率对双边交易功率的灵敏度，可以借助于线路功率对节点注入功率的灵敏度来获得。将双边交易分解成两个子交易：从功率注入点到参考节点的交易与从参考节点到功率接收点的交易。这两个交易的合成作用与双边交易的作用相当。线路功率对双边交易功率的灵敏度就等于线路功率对这两个子交易所对应的功率注入点的灵敏度之差。

线路i-j对双边交易的灵敏度kij,mn为：

式中，kij,m、kij,n分别为线路i-j对m、n两点功率的灵敏度；

s2采用三层规划方法对基于市场利益的含能效电厂的厂网协调规划进行建模，具体步骤为：

步骤s21：以阻塞成本(即发电机再调度成本)和投资成本之和最小为目标函数建立上层规划模型，上层目标函数如下：

s＝min{f1+ct,1,f2+ct,2,...,fh+ct,h,...,fh+ct,h}

阻塞成本函数表示如下：

约束条件表示如下：

约束条件包括潮流约束、发电机的增、减投标容量约束、发电机出力约束、线路输电容量约束。

以上步骤s21式中，h为基于下层电源规划结果的h种新增电源节点配置情形；ct,h为第h种情形的全网阻塞成本；th为年最大运行小时数；分别为第i个发电机增投标报价及第t阶段第y年第h种情形下的增发出力；分别为第j个发电机减投标报价及第t阶段第y年第h种情形下的减发出力；分别为发电机增投标功率的下限和上限；分别为发电机减投标功率的下限和上限；为第t阶段第y年第h种情形下的发电功率向量；为第t阶段第y年第h种情形下的负荷功率向量；为第t阶段第y年第h种情形下的系统节点导纳矩阵；为第t阶段第y年第h种情形下的电压相角向量；分别为第t阶段发电机的功率下限向量和上限向量；为第t阶段第y年第h种情形下线路ij的传输功率；为第t阶段第h种情形下线路ij的最大传输功率。

步骤s22：以投资成本最小为目标函数建立中层规划模型，投资成本包括输电线路投资成本、电厂(常规电厂和epp)投资成本以及切负荷惩罚费用，中层目标函数如下：

电源规划的投资运行模型如下：

n、n-1网络安全下的切负荷惩罚费用之和表示如下：

正常运行状态下潮流约束、线路有功潮流约束表示如下：

n-1运行状态下潮流约束、线路有功潮流约束表示如下：

输电线路约束条件表示如下：

以上步骤s22各式中，i为节点数；s为线路回路数；t为规划周期包含的阶段数；fh为第h种情形的中层目标值；r为贴现率(％)，1/(1+r)^(t-1)y为资金的折算系数；y为第t阶段包含的年数；ω为节点的集合；为第t阶段节点i到j的输电线路单位投资费用(万元/km)；lij为节点i到j之间输电线路的长度；为第h种情形下第t阶段节点i到j之间新建输电线路回数；为第t阶段新建常规电厂投资成本；为第t阶段新建能效电厂投资成本；为第t阶段常规电厂的运行维修费用；为第h种情形下第t阶段n、n-1网络安全下的切负荷惩罚费用之和；为第h种情形下第t阶段正常运行状态下节点i的切负荷量，为其列向量；为第h种情形下第t阶段第s条线路断开的n-1运行状态下节点i的切负荷量；a、b分别为正常状态下的切负荷惩罚系数和n-1状态下的切负荷惩罚系数；为第h种情形下第t阶段系统节点导纳矩阵；为第h种情形下第t阶段节点相角列向量；为第h种情形下第t阶段常规电厂节点出力列向量，分别为第t阶段常规电厂节点出力最小值和最大值的列向量；为第h种情形下第t阶段能效电厂节点出力列向量；为第h种情形下第t阶段节点负荷列向量；为第h种情形下第t阶段节点i到节点j之间原有的线路回路数；xij为节点i到j之间单条输电线路的电抗；为第h种情形下第t阶段节点i到节点j之间输电线路上的总潮流；为第t阶段节点i到节点j之间单条回路容量上限；为第t阶段节点i到j之间新建输电线路回数上限。公式中上标有“∧”符号的均代表线路n-1条件下的网络参数及对应的潮流。

步骤s23：以电厂的投资成本最小为目标函数建立下层规划模型，电厂投资成本包括新建常规电厂建设成本、新建能效电厂建设成本及运行维修成本，下层目标函数表示如下：

第t阶段常规电厂的建设成本表示如下：

第t阶段能效电厂的建设成本表示如下：

第t阶段电厂的运行维修费用表示如下，包括常规电厂的燃料成本、环境成本和维修费用以及能效电厂的运行维修费用。

各约束条件表示如下，依次为机组备用容量约束、电量约束、系统中能效电厂的容量约束、常规电厂运行时间约束、能效电厂运行时间约束、新建常规电厂机组台数约束、新建能效电厂机组台数约束。

以上步骤s23各式中m为常规电厂机组类型数；k为能效电厂机组类型数；n为第t阶段包含所选择的待建常规电厂的常规机组数目；l为第t阶段包含所选择的待建能效电厂的能效电厂数目；cg,m为新建常规发电机组类型为m的单位容量投资成本；pg,m为m型常规机组的容量；为第t阶段新建m型常规机组的台数；ce,k为新建能效电厂类型为k的单位容量投资成本；pe,k为k型能效电厂的容量；为第t阶段新建k型能效电厂的台数；为第t阶段第n个常规电厂机组的容量；iom&e,n为第n个常规电厂机组的单位运行维修费用，包括常规电厂的燃料成本、环境成本及维修费用；为第t阶段第n个常规电厂机组第y年的运行小时数；为第t阶段第l个能效电厂机组的容量；iom,l为第l个能效电厂的单位运行费用；为第t阶段第l个能效电厂机组第y年的运行小时数；th为年最大运行小时数；r为机组的备用容量系数；为第t阶段的最大负荷；α为能效电厂与负荷的最小比值；β为能效电厂与负荷的最大比值；为第t阶段第y年的负荷；为第t阶段新建m型常规机组的最大台数；为第t阶段新建k型能效电厂的最大台数。

步骤s24：对所生成的方案进行连通性校验，以确保求得的最优方案不存在孤岛网架。对存在孤岛的网架，通过随机选择孤岛与网架中节点的待架线路来消除孤岛，实现网架连通；对存在独立小网的不连通的网架，通过随机选择独立小网中节点与网架节点间的待架线路来消除独立小网，实现网架连通，最终保证了最优规划方案的网架连通性要求；

s3采用自适应遗传算法和原始-对偶内点法的混合算法对三层规划模型进行求解，具体步骤为：

步骤s31：采用自适应遗传算法对上层决策变量进行求解，并进行全局寻优；

步骤s32：采用原始-对偶内点法对中层和下层进行快速求解，并反馈至上层；

基于阻塞成本和投资成本最小的混合算法求解厂网协调规划流程图如图2所示，具体步骤如下：

(1)输入节点负荷数据、已有机组数据、待建机组数据、待建epp数据等原始参数，令阶段计数器t＝1；

(2)计算该阶段末的最大负荷和每一年末的负荷；

(3)随机生成初始种群，遗传代数计数器gen＝1；

(4)判断个体是否满足备用容量约束和epp容量约束，若满足，计算常规电厂和epp的建设费用，并以各个机组运行小时数为变量，使用内点法计算机组的运行维修费用，将建设费用和运行维修费用的总和设为下层目标函数值，若不满足，将该个体下层目标函数值置0；

(5)计算下层初始种群的目标函数值和适应度值，根据适应度值进行选择、交叉和变异操作，产生新个体；

(6)将子代作为新的原始种群，并计算子代的目标函数值和适应度值；

(7)判断遗传代数gen是否达到最大值，若达到最大值，则输出最优解及新建机组的节点配置集合，若没有达到最大值，遗传代数计数器gen＝gen+1，返回步骤(4)；

(8)给节点配置集合编号，取节点配置情况h＝1，进入中层电网规划阶段；

(9)随机生成初始种群，遗传代数计数器gen＝1；

(10)对个体进行连通性校验及修正，计算线路建设费用，并用内点法计算切负荷惩罚费用；

(11)计算上层初始种群的目标函数值和适应度值，根据适应度值进行选择、交叉和变异操作，产生新个体；

(12)将子代作为新的原始种群，并计算子代的目标函数值和适应度值；

(13)判断遗传代数gen是否达到最大值，若达到最大值，则输出最优解并存储，若没有达到最大值，遗传代数计数器gen＝gen+1，返回步骤(10)；

(14)判断h是否达到最大值，若达到最大值，则按照中层规划目标函数值由小到大进行排序，输出前m个解及对应规划方案，若没有达到最大值，h＝h+1，返回步骤(9)；

(15)给规划方案集合编号，取规划方案n＝1，进入上层规划阶段；

(16)利用内点法计算最优潮流，并计算出发电机增发出力或减发出力；

(17)根据发电机的增投标或减投标报价计算方案n的阻塞成本及上层目标函数值；

(18)判断n是否达到最大值m，若达到最大值，则输出最优解及最优规划方案，若没有达到最大值，n＝n+1，返回步骤(16)；

(19)判断t是否达到最大值，若达到最大值，则结束运算，若没有达到最大值，t＝t+1，返回步骤(2)。

实施例网络结构图如图3所示，为ieee-rts系统，该系统现有24个节点，基础总负荷为5700mw，图中实线为现有输电线路，虚线为待选输电线路。本算例中，将规划周期分为三个阶段，每个阶段为5年，负荷按每年6％的速度增长。输电线路单位投资成本均取200万元/千米，年最大运行小时数取5500小时；正常运行状态下的切负荷惩罚系数α和n-1运行状态下的切负荷惩罚系数β均取100万元/mw，中心参数σ取0.1，对偶间隙取10-7，贴现率为0.08，在matlab2014a平台上进行编程实现。

分析市场利益下不考虑能效电厂的厂网协调规划和考虑能效电厂的厂网协调规划两种情况。两种情况下各阶段厂网协调规划情况如表1、表2所示。

表1市场利益下不考虑epp的厂网协调规划数据

表2市场利益下考虑epp的厂网协调规划数据

由表1可知，不考虑epp的厂网协调规划第一阶段节点3新增300mw和600mw燃煤机组各1台，节点6新增300mw燃煤机组1台，节点18新增600mw燃煤机组2台，新增线路76条，静态投资成本为570.403亿元，动态投资成本为570.403亿元，so2排放量为57.05万吨，nox排放量为19.99万吨，co2排放量为8078.15万吨；第二阶段节点13新增300mw和600mw燃煤机组各1台，节点15新增1000mw燃煤机组1台，节点19新增600mw燃煤机组2台，新增线路35条，静态投资成本为664.3867亿元，动态投资成本为452.1704亿元，so2排放量为92.66万吨，nox排放量为31.91万吨，co2排放量为12134.97万吨；第三阶段节点6新增600mw燃煤机组1台，节点7新增390mw和220mw燃气机组各1台，节点13新增300mw燃煤机组1台，节点15新增300mw燃煤机组2台，节点19新增1000mw燃煤机组1台，节点20新增1000mw核电机组1台，新增线路15条，静态投资成本为868.7347亿元，动态投资成本为402.3923亿元，so2排放量为129.97万吨，nox排放量为44.74万吨，co2排放量为17013.27万吨。三个阶段的静态投资总成本为2103.5244亿元，动态投资总成本为1424.9657亿元，so2排放总量为279.68万吨，nox排放总量为96.64万吨，co2排放总量为37226.39万吨。规划结果如图4、图5、图6所示。

由表2可知，考虑epp的厂网协调规划第一阶段节点7新增60mw的epp1，节点9新增90mw的epp1，节点13新增70mw的epp1和70mw的epp3，节点14新增50mw的epp1，节点15新增80mw的epp1和80mw的epp3，节点18新增90mw的epp1；节点6新增600mw燃煤机组各1台，节点15新增600mw燃煤机组1台，节点18新增600mw燃煤机组1台，新增线路78条，静态投资成本为507.6063亿元，动态投资成本为507.6063亿元，so2排放量为52.15万吨，nox排放量为18.29万吨，co2排放量为7277.07万吨；第二阶段节点2新增45mw的epp3，节点3新增100mw的epp4，节点6新增70mw的epp1，节点8新增80mw的epp4，节点18新增90mw的epp4；节点13新增600mw燃煤机组各1台，节点15新增300mw燃煤机组2台，节点19新增600mw和1000mw燃煤机组各1台，新增线路54条，静态投资成本为632.1017亿元，动态投资成本为430.1978亿元，so2排放量为85.51万吨，nox排放量为29.47万吨，co2排放量为11213.05万吨；第三阶段节点1新增50mw的epp2，节点5新增50mw的epp2，节点10新增50mw的epp1和50mw的epp5，节点16新增50mw的epp3；节点3新增600mw燃煤机组1台，节点6新增600mw燃煤机组1台，节点7新增220mw燃气机组各2台，节点13新增300mw燃煤机组2台，节点18新增1000mw燃煤机组1台，节点20新增1000mw核电机组1台，新增线路14条，静态投资成本为822.2234亿元，动态投资成本为380.8485亿元，so2排放量为126.16万吨，nox排放量为43.33万吨，co2排放量为16376.83万吨。三个阶段的静态投资总成本为1961.9314亿元，动态投资总成本为1318.6526亿元，so2排放总量为263.82万吨，nox排放总量为91.09万吨，co2排放总量为34866.95万吨。规划结果如图7、图8、图9所示。