一种带蓄电池的并网光伏系统运行优化方法与流程
本发明涉及一种并网光伏系统运行优化方法,尤其是涉及一种带蓄电池的并网光伏系统运行优化方法。
背景技术:
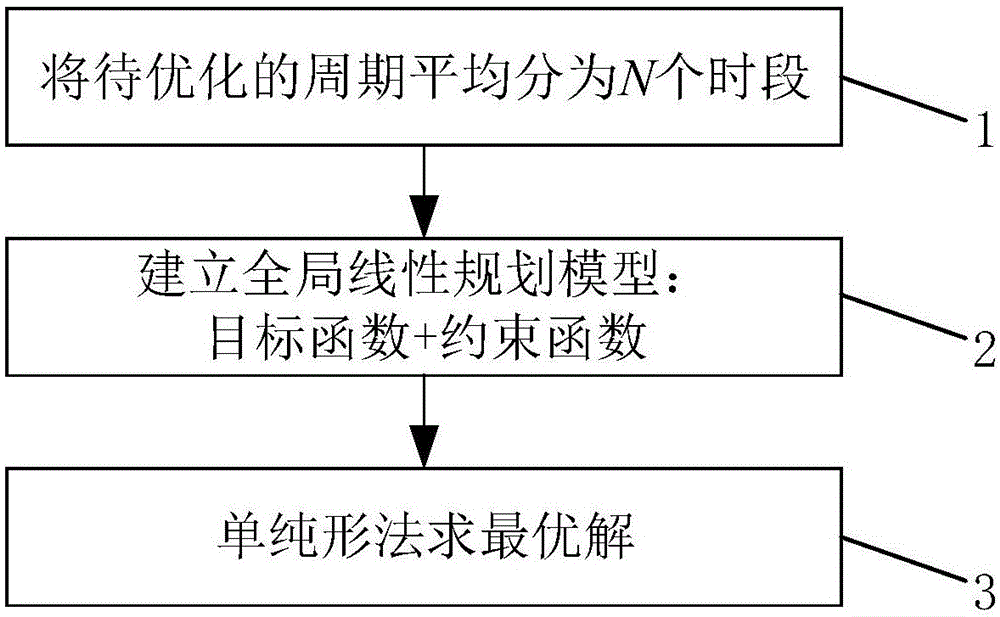
:随着传统能源的逐渐枯竭,人类社会越来越多的应用可再生能源,光伏发电是其中的一种。为了尽可能使用资源,可再生能源一般都按能够获取的最大出力发电,不具有可调节性。为了改善光伏系统的运行性能,在某些光伏系统中装有蓄电池,使其外特性包括输出功率在一定范围内可调控。带蓄电池的并网光伏系统统包括用户配网2、光伏发电单元3、蓄电池4以及负荷5,各部分相互关系及其与公共电网1之间的关系见图1。光伏发电单元3将太阳能转变成电能,电能经由用户配网2送给负荷5、蓄电池4或公共电网1。光伏发电单元3能够输出的最大功率与光伏电池本身性能(材料、面积、清洁程度)、日照(强度、角度)、环境(温度)都有关系,而日照强度和温度以日为周期变化,因此,光伏发电单元3单位能够输出的最大功率也以日为周期变化,出力集中在有日光的时段。公共电网1在未来的很长一段时间内仍将是人们生产生活用电的主要供给渠道,也将继续支撑各种新兴的分布式发电系统及微网系统的运行,担负着随时平衡其覆盖区域内电能生产和消费的重责。减小公共电网负荷的峰谷差有利于降低发、供电成本,增加全社会的能效。因此在电网中普遍实行峰谷电价或实时电价,在峰时电价较高,谷时电价较低。蓄电池4作为系统中的储能工具,通常设置多组,而每组蓄电池性能存在差异,如何进行各组蓄电池的充放电控制也成为电网调控的一项重要工作。电网调控的目标除满足电网运行质量指标外,还可进行以降低运行成本,获得最大收益为目的运行优化。在所有的优化算法中,遗传算法理论上应用范围最广,几乎可求解任何特征的优化模型。但由于该算法类似于枚举法,当控制变量数目增加时,计算量呈指数上涨,因而影响该方法的实际使用效果。技术实现要素:本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种带蓄电池的并网光伏系统运行优化方法。本发明的目的可以通过以下技术方案来实现:一种带蓄电池的并网光伏系统运行优化方法,该方法包括如下步骤:(1)将待优化的周期平均分为N个时段;(2)对整个优化周期建立全局线性规划模型,所述的全局线性规划模型包括目标函数和约束函数,其中所述的目标函数以优化周期内系统运行成本最小为目标值;(3)针对目标函数和约束函数采用单纯形法求最优解,得系统在N个时段的运行参数。步骤(2)中目标函数为:其中,F为优化周期内系统运行成本,i表示第i个时段,j表示第j组蓄电池,M为系统中蓄电池组数,Pgrid+.i为第i时段中系统向电网购电的平均功率,Pgrid-.i为第i时段中系统向电网售电的平均功率,fgrid+.i为第i时段中系统向电网购电的电价,fgrid-.i为第i时段中系统向电网售电的电价,fd.j为第j组蓄电池的折旧成本,fm.j为第j组蓄电池的维护成本,Psb+.i.j为第j组蓄电池在第i个时段的平均放电功率,Psb-.i.j为第j组蓄电池在第i个时段的平均充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率,Δt为每个时段的时长。蓄电池的折旧成本fd为:其中,Q为蓄电池生命周期内总的充放电量,Ccost为蓄电池的初始投资成本。步骤(2)中约束函数包括:(a)传输功率约束函数:其中,i表示第i个时段,Pgrid+.i为第i时段中系统向电网购电的平均功率,Pgrid-.i为第i时段中系统向电网售电的平均功率,Pgmax+.i为第i时段系统向电网购电的最大功率,Pgmax-.i为第i时段系统向电网售电的最大功率;(b)功率平衡约束函数:其中,PPV.i为第i时段光伏发电单元的有功出力预测平均值,PL.i为第i时段有功负荷功率预测平均值,Psb+.i.j为第j组蓄电池在第i个时段的平均放电功率,Psb-.i.j为第j组蓄电池在第i个时段的平均充电功率,j表示第j组蓄电池,M为系统中蓄电池组数;(c)蓄电池充放电功率约束函数:其中,Psbmax+.j为第j组蓄电池的最大放电功率,Psbmax-.j为第j组蓄电池的最大充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率;(d)蓄电池的剩余容量约束函数:SOCmin.j≤SOCi.j≤SOCmax.j,i=1,2,3…N,j=1,2,3…M,SOCi.j为第j组蓄电池第i个时段时的电池剩余容量,SOCmin.j为第j组蓄电池的最小剩余容量,SOCmax.j为第j组蓄电池的最大剩余容量;(e)蓄电池在整个优化周期内SOC恒定约束函数:其中,Δt为每个时段的时长。第j组蓄电池第i个时段时的电池剩余容量SOCi.j具体为:其中,SOC0.j为整个优化周期开始时第j组蓄电池初始剩余容量,Psb+.k.j为第j组蓄电池在第k个时段的平均放电功率,Psb-.k.j为第j组蓄电池在第k个时段的平均充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率,Δt为每个时段的时长。步骤(3)求得的系统在N个时段的运行参数包括:每个时段系统向电网购电的平均功率、每个时段系统向电网售电的平均功率、每组蓄电池在每个时段的平均放电功率以及每组蓄电池在每个时段的平均充电功率。与现有技术相比,本发明具有如下优点:(1)本发明对传统的普适模型进行改进从而建立全局线性规划模型,使得该模型能够通过采用单纯形法求最优解,求解速度快,极大地提高了求解效率;(2)本发明对传统普适模型中的目标函数和约束函数中的变量进行必要的拆解,即将第i时段中系统与电网的交互功率拆分为:第i时段中系统向电网购电的平均功率Pgrid+.i、第i时段中系统向电网售电的平均功率Pgrid-.i,将第j组蓄电池第i时段中的充放电功率拆分成两个变量:第j组蓄电池在第i个时段的平均放电功率Psb+.i.j、第j组蓄电池在第i个时段的平均充电功率Psb-.i.j,从而使由同一物理量拆出的两个决策变量成为约束方程的基变量和非基变量,即使其系数列向量尽量线性相关,以保证两个关联决策变量之一一定为0,便可应用求解效率高、全局范围寻优的单纯形法求最优解。附图说明图1为带蓄电池的并网光伏系统的结构示意图;图2为本发明带蓄电池的并网光伏系统运行优化方法的流程框图;图3为实时例光伏、负载和电价参数曲线图;图4为分时电价下的两组蓄电池充放电方案以及剩余容量变化;图5为实时电价下的两组蓄电池充放电方案以及剩余容量变化;图6为不同时段数下本发明线性模型和非线性模型运行时间对比图;图7为不同蓄电池组数下本发明线性模型和非线性模型运行时间对比图。图中,1为公共电网,2为用户配网,3为光伏发电单元,4为蓄电池,5为负荷。具体实施方式下面结合附图和具体实施例对本发明进行详细说明。实施例随着蓄电池的不断使用,蓄电池的存储容量将不断降低,直至不能使用。本发明依据法国国家太阳能研究所(NationalSolarEnergyInstitute,INES)储能实验室的研究,将蓄电池的初始投资成本(本发明暂不考虑资金使用成本)与蓄电池生命周期内的充放电总量之比,做为折旧系数,其充、放电时的折旧成本为:式中:fd为蓄电池折旧系数(元/kWh);Q为蓄电池生命周期内总的充放电量(kWh);Ccost为蓄电池的初始投资成本(元)。普适的初始优化模型,该模型为分段线性模型,从总体上看是非线性的,可采用非线性算法求解。因模型的变量个数和维数较多,所以采用非线性类算法会影响求解效率。本发明在初始优化模型的基础上通过分拆控制变量,将分段线性模型改写为全局线性模型,进而采用求解速度快、可求解出全局最优解的线性规划单纯形法进行求解,极大地提高了求解效率。(1)普适的初始优化模型及其存在的问题:a.目标函数:以用户光储系统的全日运行成本最小为目标值来进行优化。其成本费用包括光储并网系统与配电网的电能交互费用、蓄电池的折旧成本与维护成本。因此,其目标函数如下:式中:N为一个优化周期分割的时段数,M为蓄电池的组数,fd.j为第j组蓄电池的折旧成本,fm.j为第j组蓄电池的维护成本,fgrid+.i为第i时段中系统向电网购电的电价,fgrid-.i为第i时段中系统向电网售电的电价,Pgrid.i为第i时段时系统与电网之间的平均交互功率,当Pgrid.i>0时,用户系统向电网购电,此时fgrid+.i大于0,fgrid-.i=0,当Pgrid.i<0时,用户系统向电网售电,此时fgrid+.i=0,fgrid-.ifgrid-.i大于0。式(2)中,ΔSOCi.j(t)为第j组蓄电池在第i个时段内的剩余容量变化量。式中:Psb.i.j为第j组蓄电池第i时段的充放电功率,以蓄电池放电为正方向,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率;当Psb.i.j>0时,即蓄电池放电,此时η+.j大于0,η-.j=0;当Psb.i.j<0时,即蓄电池充电,此时1/η+.j=0,η-.j大于0。b.约束条件:①传输功率约束:对于用户系统与电网而言,光储并网系统与外电网交互功率也有上下限:-Pgmax-.i≤Pgrid.i≤Pgmax+.i,i=1,2,3...N(4)式中:Pgmax+.i为第i时段系统向电网购电的最大功率,Pgmax-.i为第i时段系统向电网售电的最大功率。②功率平衡约束:对于整个系统而言,在任意时段,需满足功率平衡约束:式中:PPV.i为第i时段光伏发电单元的有功出力预测平均值,PL.i为第i时段有功负荷功率预测平均值,③蓄电池充放电功率约束。-Psbmax-.j≤Psb.i.j≤Psbmax+.j,i=1,2,3…N,j=1,2,3…M(6)式中,Psbmax-.j为第j组蓄电池充电的最大功率,Psbmax+.j为第j组蓄电池放电的最大功率。④蓄电池的剩余容量(StateofCharge,SOC)约束:第j组蓄电池的放电深度不能低于其最小剩余容量SOCmin.j,充电不能超过蓄电池的最大剩余容量SOCmax.j。SOCmin.j≤SOCi.j≤SOCmax.j,i=1,2,3…N,j=1,2,3…M(7)其中,对于第j组蓄电池第i个时段时的电池剩余容量SOCij应有:式中:SOC0.j为一个优化周期开始时第j组蓄电池初始剩余容量,⑤每组蓄电池的SOC在一个优化周期始末不变:在所有约束条件中,约束条件④、⑤存在时段耦合,约束条件②存在不同性能蓄电池组间的耦合。该模型的目标函数中蓄电池剩余容量上存在绝对值符号,且蓄电池充放电效率不相同,购售电价也不相同,所以从严格意义看并不是线性模型,而是分段线性模型。如果一个优化周期分成N个时段,且整个系统中共有M组不同性能的蓄电池,则在整个优化周期内有MN个决策变量。因此如果不妥善选择优化算法,则寻优效率将非常低,影响优化方法的实际使用。因蓄电池充放电功率在同一时段不会同时进行,所以有的文献中将蓄电池充放电功率这一个物理量用两个决策变量表示,即充电功率和放电功率,但由于同一蓄电池的这两个决策变量实际为一个物理量,故在同一时段这两个决策变量一定有一个为0,所以又增添了一个非线性约束条件,即同一蓄电池在同一时段的充电功率和放电功率的乘积等于0,最后求解一个决策变量L=2MN的非线性规划,因此寻优时求解计算量较大、求解时间较长。(2)初始模型线性化的基本思路:本发明将蓄电池的充放电功率拆解为两个决策变量,且将与公共电网的交互功率也拆解为两个变量,重新列写前述初始优化模型。不同的是,本发明中不显式采用同一电池组同一时段的充放电功率的乘积为0这一约束条件,而是通过妥善的改写初始优化模型,使由同一物理量拆出的两个决策变量(本文称为关联决策变量)在约束条件中总是成对出现,并使其系数列向量尽量线性相关,以便于应用线性规划模型的单纯形法求最优解,且保证两个关联决策变量之一一定为0。线性规划的本质上为凸规划,其可行域为凸集(对于存在L个决策变量的模型,这个凸集有L个顶点),而其优解一定是可行域的某个顶点。线性规划解法——单纯形法,从一个初始可行顶点出发,通过按规则进行的表上运算,去寻找更优的顶点,直到按规则判断出再也不存在更优的顶点,则最后的那个顶点对应的决策变量的数值即为最优解。因此其优化过程中搜寻的方案不会按决策变量数呈指数增长,当决策变量较多时,单纯形算法效率明显优于其他算法。和采用非线性算法相比,因为计算量较小,求解效率较高,即使在考虑时段耦合时仍能高效找到最优解。在初始优化模型中,目标函数中蓄电池剩余容量的变化量带有绝对值符号,并且蓄电池充放电功率和蓄电池充放电效率不相同,购售电价也不相同,所以上述初始优化模型不是真正意义上的线性模型,而是分段线性模型。本发明将初始优化模型中的变量进行必要的拆解,并注意改写约束条件将其表达为符合一定规范的线性规划模型,使由同一物理量拆出的两个决策变量成为约束方程的基变量和非基变量,即使其系数列向量尽量线性相关,以保证两个关联决策变量之一一定为0,便可应用求解效率高、全局范围寻优的单纯形法求最优解在初始模型中,考虑到蓄电池充放电效率以不同数学表达作用于充放电功率,且光储用户系统向电网的购电电价与售电电价也不一定相等,需要将光储并网系统与外电网交互功率Pgrid.i拆分成两个变量:系统向电网售电功率Pgrid-.i、系统向电网购电功率Pgrid+.i,将蓄电池的充放电功率Psb.i.j拆分成两个变量:蓄电池充电功率Psb-.i.j、蓄电池放电功率Psb+.i.j。因此本发明一种带蓄电池的并网光伏系统运行优化方法,如图2所示为该方法的流程框图,包括如下步骤:(1)将待优化的周期平均分为N个时段;(2)对整个优化周期建立全局线性规划模型,所述的全局线性规划模型包括目标函数和约束函数,其中所述的目标函数以优化周期内系统运行成本最小为目标值;(3)针对目标函数和约束函数采用单纯形法求最优解,得系统在N个时段的运行参数。步骤(2)中目标函数为:其中,F为优化周期内系统运行成本,i表示第i个时段,j表示第j组蓄电池,M为系统中蓄电池组数,Pgrid+.i为第i时段中系统向电网购电的平均功率,Pgrid-.i为第i时段中系统向电网售电的平均功率,fgrid+.i为第i时段中系统向电网购电的电价,fgrid-.i为第i时段中系统向电网售电的电价,fd.j为第j组蓄电池的折旧成本,fm.j为第j组蓄电池的维护成本,Psb+.i.j为第j组蓄电池在第i个时段的平均放电功率,Psb-.i.j为第j组蓄电池在第i个时段的平均充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率,Δt为每个时段的时长。蓄电池的折旧成本fd为:其中,Q为蓄电池生命周期内总的充放电量,Ccost为蓄电池的初始投资成本。步骤(2)中约束函数包括:(a)传输功率约束函数:其中,i表示第i个时段,Pgrid+.i为第i时段中系统向电网购电的平均功率,Pgrid-.i为第i时段中系统向电网售电的平均功率,Pgmax+.i为第i时段系统向电网购电的最大功率,Pgmax-.i为第i时段系统向电网售电的最大功率;(b)功率平衡约束函数:其中,PPV.i为第i时段光伏发电单元的有功出力预测平均值,PL.i为第i时段有功负荷功率预测平均值,Psb+.i.j为第j组蓄电池在第i个时段的平均放电功率,Psb-.i.j为第j组蓄电池在第i个时段的平均充电功率,j表示第j组蓄电池,M为系统中蓄电池组数;(c)蓄电池充放电功率约束函数:其中,Psbmax+.j为第j组蓄电池的最大放电功率,Psbmax-.j为第j组蓄电池的最大充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率;(d)蓄电池的剩余容量约束函数:SOCmin.j≤SOCi.j≤SOCmax.j,i=1,2,3…N,j=1,2,3…M,SOCi.j为第j组蓄电池第i个时段时的电池剩余容量,SOCmin.j为第j组蓄电池的最小剩余容量,SOCmax.j为第j组蓄电池的最大剩余容量;(e)蓄电池在整个优化周期内SOC恒定约束函数:其中,Δt为每个时段的时长。第j组蓄电池第i个时段时的电池剩余容量SOCi.j具体为:其中,SOC0.j为整个优化周期开始时第j组蓄电池初始剩余容量,Psb+.k.j为第j组蓄电池在第k个时段的平均放电功率,Psb-.k.j为第j组蓄电池在第k个时段的平均充电功率,η+.j为第j组蓄电池放电时的效率,η-.j为第j组蓄电池充电时的效率,Δt为每个时段的时长。步骤(3)求得的系统在N个时段的运行参数包括:每个时段系统向电网购电的平均功率、每个时段系统向电网售电的平均功率、每组蓄电池在每个时段的平均放电功率以及每组蓄电池在每个时段的平均充电功率。利用Matlab软件对优化模型进行编程,并调用单纯形法进行求解。分别采用分时电价算例和实时电价算例对上述改进优化模型进行验证。原始数据与结果如下。本实施例中将一天24小时作为一个优化周期,并将24小时平均分为24个时段,每个时段为1小时。(1)分时电价算例选取两组参数不同的蓄电池组,如表1。同时将一天分为24个时段的分时电价,谷时段为00:00—08:00、11:00—13:00和22:00—24:00,平时段为09:00—12:00、14:00—19:00和21:00—22:00,峰时段为19:00—21:00,对应的电价、预测光伏、预测负荷在本文中作为已知数据,如图3所示。表1两组蓄电池参数根据本文提出的优化模型,在MATLAB环境运行,得出两组蓄电池在各个时段的充放电功率方案。图4是用本发明全局线性规划模型得到的优化结果,左轴表示蓄电池充放电功率,其零线以上表示充电,以下表示放电,右轴表示蓄电池的剩余容量。为了方便比对分析,在该图中还画出了电价趋势。可以看出,随着电价在一天内经历两次峰谷,两组蓄电池也经历了两次充放电,蓄电池充电的时段对应购售电价的谷时段,放电对应购售电价的峰时段。而且蓄电池的第二次放电没有在充电后的次高电价马上进行,而是等到了更高时段进行放电,以取得更大收益,这是因为本模型考虑了时段耦合,蓄电池的最佳充放电方案是对一个完整的充放电周期的全局优化的结果。如果不考虑时段耦合,优化按照时间顺序一个一个时段依次进行,过去时段的输出,作为下一个时段优化的输入,进行某一时段决策时不考虑优化周期内未来时段的电价变化对本时段优化决策的影响,会使得蓄电池的第二次放电不一定出现在峰时段,系统的收益不一定能达到最优。同时,蓄电池的充放电方案满足各个约束条件,包括蓄电池的SOC在一个充放电周期内的变化量之和为0这个约束。(2)实时电价算例本模型不仅适用于分时电价,同时也适用于实时电价。同样,取两组蓄电池在实时电价下进行仿真。图5中放入实时电价趋势,在5、8、10、14、15、19时电价最大,为1.123元/kWh;在11时电价最小,为0.357元/kWh。从图中可以看出,0-1时段、5-7时段、10-11、16-17时段电价低,蓄电池组充电;4-5时段、7-8时段、9-10时段、13-14时段、18-19时段电价高,蓄电池组放电;1-4时段、8-9时段、11-13时段,电价虽较高,但紧接该时段,会有更高电价,故蓄电池组在前一时段充电之后维持不变,到更高电价时放电;14-16时段、19-24时段,蓄电池组剩余容量达到最小值,既不充电也不放电。从图5可以看出两组蓄电池在一个周期中,经过了多次的充放电,而且,两组蓄电池的充放电时段是相对应的。同时,也不难发现,当电价比较低时,两组蓄电池充电,但并不是在下个时段就开始放电,而是在接下去的一块区域中的某一个高电价时进行放电,进而使得系统的利益在整个优化周期内最大化,充分体现了考虑时段耦合的好处。为了验证所提线性规划模型的求解效率和精度,分别求解不同时段数、不同蓄电池组数的日前计划模型,并与非线性规划模型进行比较。非线性规划模型选用某文献的做法,为保证拆解的两个变量之一为零,将两个变量相乘为零,进而保证保证拆解的两个变量之一一定为零。即增加约束条件:Psb+.i.j×Psb-.i.j=0i=1,2,3…N、j=1,2,3…M,Pgrid+.i×Pgrid-.i=0i=1,2,3…N。a.时段数不同在实时电价下,一天可能不止分为24个时段,下面把一天分为24,48,96个时段,对比两种算法的求解时间。取两组参数不同的蓄电池组,在matlab环境下进行仿真,求解时间如图6所示,目标函数值如表2所示。表2不同时段下线性模型与非线性模型的目标函数值(单位:元)24个时段48个时段96个时段线性1575.91722.31750.9非线性1580.81813.11776.3对于优化结果而言,在不同的时段下得到的非线性模型与本模型得到的目标函数值近似相等,且采用本模型后目标函数值更小,即更具优越性。从运行时间上看,随着时段数不断增加,本模型的所需的运行时间也在增加,但增加量不大可以近似忽略,而非线性模型所对应的仿真时间增加量很明显,其增长方式呈现指数增长趋势,从48个时段到96个时段的时间更是突增至665s。两种模型对应所需的时间相差几十倍甚至几百倍。随着时段数的增加,这个差距也在不断的扩大,因此对于相同蓄电池组数,不同分时电价的时段数而言,本模型的运算速率明显快于非线性模型。b.组数不同在96个时段的实时电价环境下,取各个参数不同的蓄电池组,比较非线性模型与本模型的运行时间及优化结果,运行时间如图7所示,优化结果如表3所示。表396时段不同蓄电池组数线性模型与非线性模型的目标函数值(单位:元)2组3组4组5组线性1750.91706.61675.41614.3非线性1776.31754.31724.91728.4由图7可以看出,不同蓄电池组数下,本发明的全局线性规划模型(线性)对应的运行时间依旧很少,近似可以忽略。非线性模型所对应的运行时间在3组蓄电池及以上增加量不多,却依然保持着增长的趋势。两个模型对应时间的数量级相差几百倍甚至几千倍。对于优化结果而言,目标函数值近似相等,对于最小优化而言,线性规划所获得的结果更为准确。由此可见,本模型无论从计算时间还是精度,本发明的全局线性规划模型都能够准确且快速地应用于用户光储系统的经济运行调度。当前第1页1 2 3
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1