一种电力系统电气距离可视化方法和装置与流程
本发明提供的技术方案涉及大电网稳定与控制领域,具体讲涉及一种电力系统电气距离可视化方法和装置。
背景技术:
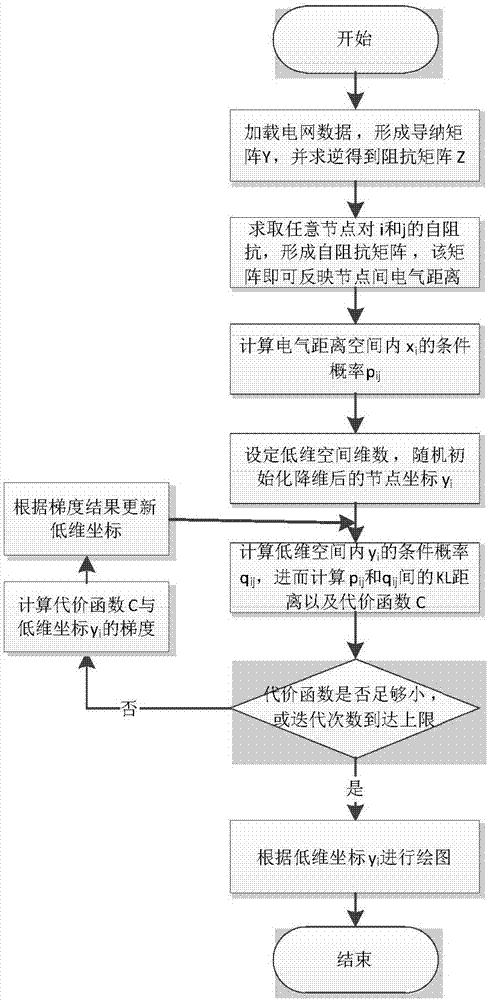
:随着经济水平的飞速提升,对电力的需求量也日益增加,为了适应经济的发展,随之建成了西电东送、全国联网以及特高压输电等重大工程,交直流混联的特大电网。随着电网规模的扩大,电网安全稳定性提出了更高的要求。世界上曾发生的多次电网故障表明输电电压等级的提高、联网规模的扩大以及传输容量的增加,电网故障所带来的危害性也越大,电网故障的原因和过程也更为复杂。作为决定电网稳定特征的重要参数之一的电气距离,伴随着电网规模的扩大和运行方式的增多,情况更加多样化,也决定着确保电网稳定运行采取的措施更加复杂;电气距离的在线监测及其可视化,也成为电力系统在线分析与预警的重要组成部分之一。现有的电力系统可视化方法大多以地理图或单线图表现设备间的连接关系,主要用于电网运行状态监测,但无法直接表现电网的稳定特性。因此需要提供一种能对运行电网进行的在线监视、分析和控制,保障电力生产、传输和使用安全的一种技术方案。技术实现要素:为满足现有技术发展的需要,本发明提供一种新型的电力系统电气距离可视化方法。本发明提供的电力系统电气距离可视化方法,其改进之处在于,所述方法包括根据预先采集的电力系统的电网拓扑和运行参数用节点导纳矩阵求逆的方法计算节点自阻抗矩阵;根据自阻抗矩阵,用t-sne算法将高维空间数据映射到低维空间计算电气距离;根据低维空间计算得到的节点坐标,绘制电力系统电气距离相关图形。进一步的,所述自阻抗矩阵的计算包括:(1)用遍历电网内部的支路形成节点导纳矩阵y,并对y矩阵求逆运算,得到节点阻抗矩阵z;(2)计算节点i和节点j组成的节点对的自阻抗:zij,ij=zii+zjj-2*zij,并计算节点对自阻抗复数的幅值,保存上三角矩阵的数值。进一步的,所述电气距离的计算包括:根据自阻抗矩阵,将高维空间数据映射到低维空间,以电气距离空间和低维空间内条件概率的kl距离最小化为目标,以低维空间内每个节点的坐标为参数进行迭代优化计算,并输出低维空间的节点坐标,计算低维空间的电气距离。进一步的,用下式表示高维数据集x中点xj出现在点xi附近的条件概率pj|i:其中,σi为点xj与点xi的方差;用下式表示高维数据集x中点xi出现在点xj附近的条件概率pi|j:t-sne算法中高位空间的条件概率如下式所示:其中,n为原始数据点的总数;低维空间的数据集y中的条件概率如下式所示:进一步的,所述kl距离用下式所示的代价函数c表示:其中,kl(pi||qi):节点i在高维空间和低维空间分别形成的条件概率pi和qi的kl距离。进一步的,代价函数c的计算包括:(1)随机初始化yi的值,将yi随机设为[0,1]×[0,1]范围内的坐标;(2)按下式计算代价函数c关于低维数据集点坐标yi的偏导数:(3)按下式更新坐标yi的值:式中,η:步长或者学习率,为正数。进一步的,判断代价函数c是否足够小或迭代次数是否到达上限:若代价函数c足够小或迭代次数到达上限,则根据低维坐标yi进行绘图;否则,重新计算代价函数c与低维坐标yi的梯度,并根据梯度更新低维坐标。进一步的,所述电力系统电器距离相关图形的绘制包括:根据低维空间中计算出的节点坐标,在二维或三维空间进行选择性绘图。一种电力系统电器距离可视化装置,所述装置包括:矩阵创建单元,用于根据采集的电网拓扑和运行参数计算自阻抗矩阵;降维单元,基于自阻抗矩阵用t-sne算法降维运算电气距离;绘图单元,用于根据降维结果绘制电气距离图。进一步的,所述矩阵创建单元包括:采集子单元,用于遍历电网内支路,采集电网拓扑和运行参数;所述降维单元,根据电气距离空间和低维空间内条件概率的kl距离,通过确定低维空间内各点的坐标yi使得代价函数c最小,完成电气距离由高维空间到低维空间的降维运算。与最接近的现有技术比,本发明提供的技术方案具有以下优异效果:1、本发明提供的技术方案从电力系统电气距离的角度出发,以t-sne算法实现降维运算,把设备之间高维、复杂的电气距离关系映射到低维度的二维或三维空间,根据低维空间内的节点坐标绘制图形,根据绘制的图形可以展示高维度空间中不同设备间关系,为技术人员提供参考和技术支撑,给运行技术人员以高维度空间电力系统设备间关系的直观的印象。2、本发明提供的技术方案的结论可进一步应用于同调机群分析、灵敏度分析、薄弱环节辨识等电网稳定的分析方法中。附图说明图1为本发明提供的可视化方法流程图;图2为原始ieee-118系统可视化结果;图3为实施例中断开23-24支路后ieee-118系统可视化结果;图4为实施例中某日两华电网可视化结果。具体实施方式以下将结合说明书附图,以具体实施例的方式详细介绍本发明提供的技术方案。电气距离是指电力系统中任意两个节点之间的联系阻抗,阻抗值小代表这两点间的联系紧密,相互影响作用明显。电气距离与地理距离之间没有必然的联系,它主要取决于电压等级、两点之间直接或间接连接的支路数量以及支路阻抗大小等因素。本发明中求解电力系统电气距离的求解方法为节点导纳矩阵y求逆方法,主要包括:1.遍历电网内全部支路(包括交流线和变压器),形成节点导纳矩阵y;2.对y矩阵进行求逆,得到节点阻抗矩阵z;3.任意节点对i和j的自阻抗:zij,ij=zii+zjj-2*zij;4.求取每个节点对自阻抗复数的幅值,由于节点对自阻抗矩阵为对称矩阵,且对角线数值为0,因此只需保存上三角矩阵的数值即可。高维的数据集不便于直接观察以发现其隐藏的特性,sne(stochasticneighborembedding)算法采用非线性降维的方法将高维的数据映射到三维或者二维空间,这样就能在立体图或者平面图中比较直观地展示数据的分布情况。sne算法的设计原则是在映射的过程中保持数据点之间的距离关系,即在原始高维空间中距离较近(或较远)的点映射到低维空间后对应点的距离也较近(或较远)。距离远近反应的是数据点之间的相似程度。欧式距离是表示距离的一种常用方法,设xi,xj为原始高维空间中的任意两点,yi,yj为其映射到低维空间中的点,||xi-xj||2和||yi-yj||2分别表示其欧式距离。sne算法在欧式距离的基础上提出了一种条件概率来表示数据点的远近程度。在高维数据集x中该条件概率定义为:pj|i表示点xj出现在点xi附近的条件概率,它采用高斯分布的形式,σi为其对应的方差。xj与xi相隔越近,pj|i越大,说明它们之间的相似度越高。设定pi|i=0。在低维数据集y中也用类似的条件概率表示数据点的远近程度,其定义如下:qj|i表示点yj出现在点yi附近的条件概率,其高斯分布的方差设定为设定qi|i=0。这样对于任意的i,在高维空间和低维空间中分别形成一个条件概率分布pi和qi。为了保持映射前后数据点之间的距离关系,pi和qi应尽量保持一致。kl(kullback-leibler)距离是衡量两个概率分布一致性的常用方法。对于所有的i,pi和qi之间的kl距离为:c即为sne算法的代价函数,其值越小,分布越一致。可以通过梯度下降算法来求解yi使得其值最小。yi可以是二维或者三维坐标,求解出来后即可在用平面图或者立体图中标示出来。t-sne是sne的改进算法,主要解决了sne算法中的两个问题:不对称问题和拥挤问题。不对称问题:sne算法定义的条件概率是不对称的,即pj|i≠pi|j,qj|i≠qi|j,按照常理,两点之间的距离或者相似度应该是唯一的,所以它们应该相等。为此,t-sne算法在上面的基础之上重新定义了pj|i和qj|i,并记为pij和qij:式(4)中n为原始数据点的总数,这样定义的pij和qij均满足对称性。拥挤问题:数据降维可视化的理想效果是把相似或者相近的点聚在一簇,不同类别的簇尽量分隔开。sne算法中高维空间和低维空间的条件概率均采用高斯分布,假设求解后分布大概一致,由于空间维度的减小,低维空间中不同类别的簇势必也会挨着很近,造成拥挤。为了解决该问题,t-sne算法将式(5)中低维空间中的条件概率分布继续进行改进,最终变换成如下的t-分布:t-分布与高斯分布相比,中心部位偏低,尾部偏高偏长。为了满足pij=qij,在高维空间中相近的点映射到低维空间中后点的距离更近,高维空间中隔得较远的点映射到低维空间中点的距离更远。这样就使得同一类的点聚得更紧,不同类的点分隔得越开。本发明提供的技术方案的主要步骤包括:(1)求取自阻抗矩阵;(2)采用t-sne算法进行降维;(3)根据降维后坐标进行绘图。具体包括:a)求取自阻抗矩阵基于电网拓扑和运行参数,形成导纳矩阵y;求逆得到阻抗矩阵z;根据公式zij,ij=zii+zjj-2*zij形成节点对的自阻抗矩阵。该矩阵即可反映任意两节点间的电气距离。b)t-sne算法进行降维以电气距离空间和低维空间内条件概率的kl距离(式3-6)的最小化为目标,以低维空间内每个节点的坐标为参数,进行迭代优化计算。当kl距离足够小或迭代次数到达上限时,迭代计算结束,输出低维空间的节点坐标。kl(kullback-leibler)距离是衡量两个概率分布一致性的常用方法。对于所有的i,pi和qi之间的kl距离为:sne算法定义的条件概率是不对称的,即pj|i≠pi|j,qj|i≠qi|j,按照常理,两点之间的距离或者相似度应该是唯一的,所以它们应该相等。为此,t-sne算法在上面的基础之上重新定义了pj|i和qj|i,并记为pij和qij:式(4)中n为原始数据点的总数,这样定义的pij和qij均满足对称性。根据式(3)的电气距离空间和低维空间内条件概率的kl距离,将高维空间和低维空间的条件概率代入kl距离公式,pij可通过上面的电气距离直接求得,qij是低维空间各点坐标yi的函数,从而c也为yi的函数。算法的重点是确定yi使得c最小,具体过程如下:1)随机初始化yi的值,比如本专利中的二维可视化,将yi随机设为[0,1]×[0,1]范围内的某个坐标;2)计算c关于yi的偏导数:3)更新yi的值:η称为步长或者学习率,为正数,可根据c的收敛情况适当调整;重复上述迭代过程,直到c值大致收敛,上述算法即为梯度下降求最小值过程。求得的yi值为各电气节点在低维(此处是二维)空间的坐标,其距离能大致反映出各节点间的电气距离。c)根据降维结果进行绘图;根据第2步的节点坐标,在二维或三维空间中进行绘图,通过图形可直观地感受到各个节点间的远近程度。本步骤可根据用户需要进行选择性绘制,例如可以只绘制电厂节点展示电厂间的紧密程度,或者只绘制某一区域或电压等级的节点等。本发明提供了一种电力系统电器距离可视化装置,所述装置包括:矩阵创建单元,用于根据采集的电网拓扑和运行参数计算自阻抗矩阵;所述矩阵创建单元包括用于遍历电网内支路、采集电网拓扑和运行参数的采集子单元;降维单元,基于自阻抗矩阵用t-sne算法降维运算电气距离;根据电气距离空间和低维空间内条件概率的kl距离,通过确定低维空间内各点的坐标yi使得代价函数c最小,完成电气距离由高维空间到低维空间的降维运算。绘图单元,用于根据降维结果绘制电气距离图。实施例采用ieee-118节点的标准测试系统,该系统含有118个节点,其中54个为发电机节点,此外还有191个交流线支路和9个变压器支路。在全连接模式下,通过本发明算法可得到如图1所示的可视化结果,进一步采用kmeans聚类分析,可得到7个聚类结果,如表1所示,可见聚类结果与可视化效果是一致的,也就是说本发明的可视化方法可以很好的反映各节点间的电气距离和相互间的紧密程度。表1原始ieee-118系统的kmeans分类结果组号所含母线编号母线数量1.1-14,16,117162.15,17-33,113-115213.34-43104.44-64,66,67235.65,68-81,98,116,118186.82-97,101,102187.99,100,103-11212进一步把节点23和节点24之间的支路断开,其余不变,经本发明算法分析可得到如图2的可视化结果,对比图1可见,支路23-24运行时,两节点间电气距离较近,断开后则需要经过多条支路进行远距离互联,电气距离较远,两图的可视化结果很好地展示了这一变化。再次进行kmeans分类可见,节点23和24分别被归入了不同的分组。表2断开23-24支路后ieee-118系统的kmeans分类结果组号所含母线编号母线数量1.1-14,16,117162.15,17-23,25-33,113-115203.34-43104.44-64,66,67235.24,65,68-81,98,116,118196.82-97,101,102187.99,100,103-11212以国家电网公司某日在线计算数据为基础,验证本方法的有效性。当月华北-华中处于联网运行状态,因此在线数据中包含国调直调以及华北、华中所有220kv以上的电网设备(注:所用在线数据中不包含蒙东电网数据)。图4展示了两华电网中各发电厂之间电气距离的可视化结果,图中从上到下、从左到右分别对应:四川+重庆、冀北+河北+山西、江西、湖北、湖南、山东、河南。可见,省内电厂间的电气距离通常小于省间,尤其是江西、湖北、湖南三个群较为紧密,而四川电网由于有不少的小水电厂比较分散,相互间联系较为薄弱,因此占据了整个画面的较大的面积。上述可视化结果与两华电网特征相一致,验证了本发明的有效性。以上实施例仅用以说明本发明的技术方案而非对其限制,尽管参照上述实施例对本发明进行了详细的说明,所属领域的普通技术人员依然可以对本发明的具体实施方式进行修改或者等同替换,这些未脱离本发明精神和范围的任何修改或者等同替换,均在申请待批的本发明的权利要求保护范围之内。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1