一种DFIG网侧及转子侧PWM变流器的运行控制方法与流程
本发明属于电力系统领域,涉及并网型风力发电系统及其控制,具体涉及到一种风力发电系统电磁暂态数学建模及其软件仿真技术与方法。
背景技术:
作为新能源发电之一,风力发电已经成为当今世界上规模化开发程度最高、技术最成熟和发展速度最快的可再生能源之一。近年来,风力发电技术在全世界范围内发展迅速,风力发电系统正在经历从小容量到大容量、从单风机系统向大规模风电场、从陆上风电向海上风电发展过渡的时期。
双馈风力发电系统采用双PWM变流器进行励磁控制,具有有功和无功功率解耦控制的优点,从而能够调节发电机输出的有功和无功功率,具有与同步机类似的系统调节能力,能够对电网频率和电压起到调节和支撑的作用。大多数风电场双馈风力发电机主要以单位功率因数方式运行,未能充分发挥其功率调节能力参与电网调节。存在如何最大限度发挥双馈风力发电系统无功功率调节性能,以满足电网多目标需求问题,对双变流器协调控制策略进行深入研究是解决该问题的关键,开展双馈风力发电系统双PWM变流器控制策略研究,具有重要的理论价值和工程实际意义。
技术实现要素:
基于现有技术存在的问题,本发明提出了一种DFIG网侧PWM变流器的运行控制方法,具体为:
导出基于d轴电网电压定向(ugq=0)、dq分量形式的网侧变流器交流侧电压表达式为:
其中,Lg和Rg分别为网侧变流器的并网电抗和及其等效电阻,igd和igq分别为网侧变流器的d轴和q轴电流,ugd为电网电压d轴分量,ω1为电网电压的角频率;
式(10)表明网侧变流器d轴、q轴电流除受vgd、vgq的控制以外,还受电流交叉耦合项ω1Lgigq、ω1Lgigq,电压降Rgigd、Rgigq以及电网电压ugd的影响;设:
为了消除控制静差,引入积分环节,设计如下电流控制器:
式中,分别为d、q轴电流参考值,kigp、kigi分别为电流控制器的比例、积分系数;
式(12)给出了电流控制器的输出电压,代入式(10)可得网侧变流器交流侧电压参考值:
式(13)表明,由于引入了电流状态反馈量ω1Lgigq、ω1Lgigq来实现解耦,同时又引入了电网扰动电压项和电压降项Rgigd、Rgigq进行前馈补偿,从而实现d、q轴电流的解耦控制;
直流环节电压控制器可采用类似式(12)所示电流控制器的方式来设计,即:
式中,为直流母线电压参考值,kvp、kvi分别为直流电压控制器的比例、积分系数;
此外,网侧变流器直流侧与交流侧的功率平衡关系为:
则d轴电流的参考值可由式(13)、式(14)和式(15)求得为:
即实现网侧PWM变流器的运行控制。
为解决上述问题,本发明还提出了一种DFIG转子侧PWM变流器的运行控制方法,具体为:
同步速旋转坐标系的d轴定向与定子磁链矢量Ψs时,有:
ψsd=|Ψs|=ψs,ψsq=0 (17)
其中,ψs为定子磁链矢量的幅值;|Ims|为定子励磁电流矢量幅值,在理想电网电压条件下,视为常量;Lm为互感;imsq为定子励磁电流q轴分量;ψsq为定子磁链q轴分量。
定子磁链幅值和坐标变换用空间位置角度θ1可通过定子磁链矢量的αβ分量来计算:
式中,Rs为定子电电阻;ψsα、ψsβ分别为定子磁链矢量的α、β分量;usα、usβ分别为定子电压矢量的α、β分量;isα、isβ分别为定子电流矢量的α、β分量;
根据定子磁链定向下DFIG的定子有功、无功功率表达式为:
其中,Us为定子电压;Pcus、ψs分别为定子绕组铜耗和定子磁链;Pes为定子输出的励磁功率;为定子电流矢量的共轭矢量;
定子铜耗相对于电磁功率很小,在功率控制时,忽略不计,可得:
根据式(23),化简可得到:
其中,ird为转子电流的d轴分量;为转子电流矢量的共轭矢量;
由式(23)和式(24)可以看出,采用定子磁链定向后,控制转子电流q轴分量就可以控制DFIG定子输出有功功率,控制转子电流d轴分量就可以控制DFIG定子输出无功功率,实现了有功和无功功率的解耦控制。
设计转子电流的闭环控制器时,可将转子电压矢量方程写成d、q分量形式:
其中,Lr、Rr分别为转子绕组电阻和转子等效两相绕组自感;ψrd、ψrq分别为转子磁链的d、q轴分量;ird、irq分别为转子电流的d、q轴分量;ωslip、σ分别为为转差电角速度和为发电机的漏磁系数;
由于采用定子磁链定向,将转子磁链用定子磁链和转子电流来表示:
式中,Ls为dq坐标系中定子等效两相绕组自感;
将式(26)代入式(25)中,得到:
式(27)表明,转子d、q轴电压除受到id、iq的控制以外,还受到电流交叉耦合项,转子电压降以及定子磁链的影响;
按式(28)引入中间变量:
为消除静差,引入积分环节,按式(27)设计如下电流控制器:
其中,分别为转子d、q轴电流参考值,kirp、kiri分别为转子电流控制器的比例、积分系数。
将式(29)代入式(27)中,得到:
式(30)表明,通过引入电流交叉耦合项,转子电压降以及定子磁链前馈补偿,从而实现了d、q轴电流的解耦控制。
本发明的有益效果:针对并网型风力发电系统仿真分析的工程需求,本发明建立了双馈型感应风力发电机(DFIG)网侧PWM变流器数学模型,设计了基于d轴电网电压定向的网侧变流器控制方法,实现电流跟踪控制和逆变器直流母线电压均衡控制。建立了转子侧变流器数学模型,设计了定子磁链定向的DFIG转子电流控制方法。通过在PLECS软件平台下搭建了2MW双馈异步发电机仿真分析模型,对次同步状态、超同步状态,以及次同步到超同步状态之间的过渡过程进行了详细分析,结果表明所设计的数学模型和控制方法是可行的,本发明的方法可以进一步拓展到大规模风电场接入电网的稳态和动态特性研究。
附图说明
图1 DIFG网侧PWM变流器的主电路示意图;
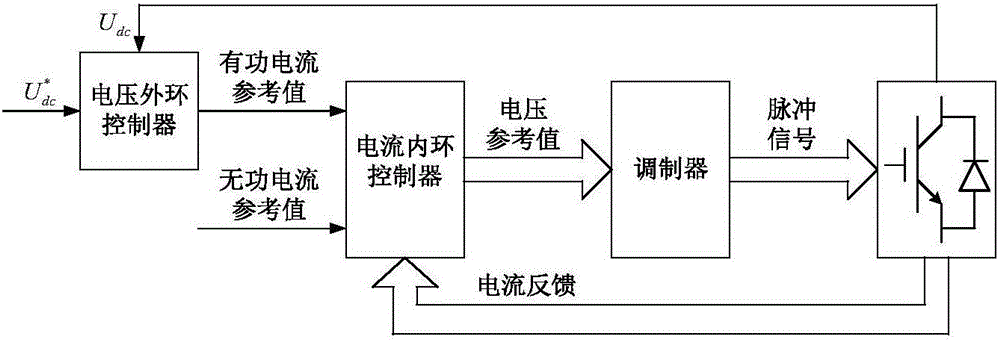
图2网侧变流器控制系统结构示意图;
图3基于d轴电网电压定向的网侧变流器控制框图;
图4基于定子磁链定向的DFIG转子电流控制框图;
图5基于PLECS的DFIG风电系统仿真框图;
图6次同步稳态运行时DFIG定、转子和总输出有功、无功功率(a)有功功率(b)无功功率示意图;
图7次同步稳态运行时DFIG转子电流、电压(a)转子电压(b)转子电流示意图;
图8次同步稳态运行时DFIG定子输出电流、电压(a)定子电压(b)定子电流示意图;
图9超同步稳态运行时DFIG定、转子和总输出有功、无功功率(a)有功功率(b)无功功率示意图;
图10超同步稳态运行时DFIG转子电流、电压(a)转子电压(b)转子电流示意图;
图11超同步稳态运行时DFIG定子输出电流、电压(a)定子电压(b)定子电流示意图;
图12过渡过程DFIG定、转子和总输出有功、无功功率(a)有功功率(b)无功功率示意图;
图13过渡过程中DFIG的转子电流、电压(a)转子电压(b)转子电流示意图;
图14过渡过程电网侧相电压、电流与直流母线电压(a)相电压(b)相电流(c)直流母线电压示意图;
图15过渡过程转子转速与转矩(a)转子转速(b)转子转矩示意图。
具体实施方式
下面结合附图对本发明的实施例做进一步的说明。
具体从以下几个方面进行说明:
建立DFIG网侧PWM变流器数学模型
双馈型风力发电机网侧变流器的主电路如图1所示。图中,uga、ugb、ugc分别为三相电网的相电压;iga、igb、igc分别为三相输入电流;vga、vgb、vgc分别为变流器交流侧三相电压;Udc为变流器直流侧电压;C为直流母线电容;iload为直流侧的负载电流。主电路中,Lga、Lgb、Lgc分别为每相进线电抗器的电感;Rga、Rgb、Rgc分别为包括电抗器电阻在内的每相线路电阻。在DFIG风电系统中,网侧变流器的负载则是转子侧变流器。
假设图1中的功率器件均为理想器件,则可以得到三相静止坐标系中网侧变流器的数学模型:
式中,Sga、Sgb、Sgc分别为三相PWM变流器中各桥臂的开关函数,且定义上桥臂功率元件导通时为1,下桥臂功率元件导通时为0。
考虑到励磁变流器一般采用三相无中线的接线方式,根据基尔霍夫电流定律可知,无论三相电网电压平衡与否,其交流侧三相电流之和应为0,即:
iga+igb+igc=0 (4)
构造恒等式:
考虑A、B、C三相进线电抗器的电感、电阻相等,即Lga=Lgb=Lgc,Rga=Rgb=Rgc。将式(1)、式(2)和式(3)相加,在将式(4)代入,得到:
网侧变流器交流侧的三相电压与各桥臂开关函数Sga、Sgb、Sgc之间关系为:
转换成相电压关系为:
将式(8)代入式(6),得到:
在以上的公式推导中,只假设了三相进线电抗器的电感、电阻的相等,没有对电网电压做任何假设,故在电网电压波动、三相不平衡、电压波形畸变(谐波)等各种情况下,改方程均有效适用。
DFIG网侧PWM变流器的运行控制策略:
网侧变流器主要功能是保持直流母线电压稳定、输入电流正弦和控制输入功率因数。直流母线电压稳定与否取决于交流侧与直流侧有功功率的平衡,如果能有效地控制交流侧输入有功功率,则可以保持直流母线电压的稳定。
在电网电压恒定的条件下,交流侧有功功率的控制就是对输入电流有功分量的控制;对功率因数的控制就是对输入电流无功分量的控制;而输入电流波形正弦与否主要与电流控制的有效性和调制方式有关。由此可见,整个网侧变流器的控制系统可分为两个环节:电压外环控制和电流内环控制,如图2所示。
可以导出基于d轴电网电压定向(ugq=0)、dq分量形式的网侧变流器交流侧电压表达式为:
式(10)表明网侧变流器d、q轴电流除受vgd、vgq的控制以外,还受电流交叉耦合项ω1Lgigq、ω1Lgigq,电压降Rgigd、Rgigq以及电网电压ugd的影响。因此,要实现对d、q轴电流的有效控制,必须找到一种能解除d、q轴电流间耦合和消除电网电压扰动的方法。设:
通过引入积分环节到式(9),设计如下电流控制器消除控制静差:
式中,分别为d、q轴电流参考值,kigp、kigi分别为电流控制器的比例、积分系数。
式(12)给出了电流控制器的输出电压,代入式(10)可得网侧变流器交流侧电压参考值:
式(13)表明,由于引入了电流状态反馈量ω1Lgigq、ω1Lgigq来实现解耦,同时又引入了电网扰动电压项和电压降项Rgigd、Rgigq进行前馈补偿,从而实现了d、q轴电流的解耦控制,有效提高了系统的动态控制性能。为了提高网侧变流器的抗负载扰动性能,还可以加上负载电流前馈补偿项。
直流环节电压控制器可采用类似于式(12)所示电流控制器的方式来设计,即:
其中,为直流母线电压参考值,kvp、kvi分别为直流电压控制器的比例、积分系数。
考虑在图1中,忽略各种损耗功率,如交流侧线路电阻损耗、PWM变流器开关和导通损耗等,网侧变流器直流侧与交流侧的功率平衡关系为:
因此,d轴电流的参考值可由式(13)、式(14)和式(15)求得为:
根据式(14)、式(15)和式(16),可画出带解耦和扰动补偿的网侧变流器直流环节电压、电流双闭环控制框图,如图3所示。
DFIG转子侧PWM变流器的电磁暂态数学模型及其控制策略,
双馈异步风力发电机的转子侧变流器主要用于DFIG的功率控制。由于直流环节的解耦作用,交流励磁变流器中各变流器的功能独立,其中网侧变流器并不直接参与对DFIG的控制;转子侧变流器则是用以实现DFIG及整个风电系统的运行控制,其控制的有效性将直接影响DFIG风电系统的运行性能。
DFIG风电系统的主要运行目标有两个,首先是变速恒频前提下实现最大风能追踪,关键是DFIG转速或功率的控制;其次是DFIG输出无功功率的控制,以保证所并电网的运行稳定性。由于DFIG输出的有功和无功功率与转子的d、q分量电流密切相关,转子侧变流器的控制目标就是实现对转子两分量电流的有效控制,其控制策略应以转子侧变流器即DFIG数学模型为基础来进行设计。
当同步速旋转坐标系的d轴定向与定子磁链矢量Ψs时,有:
ψsd=|Ψs|=ψs,ψsq=0 (17)
式中,ψs为定子磁链矢量的幅值;|Ims|为定子励磁电流矢量幅值,在理想电网电压条件下,他们可以看作为常量。定子磁链幅值和坐标变换用空间位置角度θ1可通过定子磁链矢量的αβ分量来计算:
式中,ψsα、ψsβ分别为定子磁链矢量的α、β分量;usα、usβ分别为定子电压矢量的α、β分量;isα、isβ分别为定子电流矢量的α、β分量。在实际应用中,通常用低通滤波器来取代式(19)中的纯积分环器,以避免因初始值或干扰而造成的直流偏置。
根据定子磁链定向下DFIG的定子有功、无功功率表达式为:
定子铜耗相对于电磁功率很小,在功率控制时,可忽略不计,可得:
根据式(23),化简可得到:
由式(23)和式(24)可以看出,采用定子磁链定向后,控制转子电流q轴分量就可以控制DFIG定子输出有功功率,控制转子电流d轴分量就可以控制DFIG定子输出无功功率,实现了有功和无功功率的解耦控制。
设计转子电流的闭环控制器时,可将转子电压矢量方程写成d、q分量形式:
由于采用定子磁链定向,将转子磁链用定子磁链和转子电流来表示:
将式(26)代入式(25)中,得到:
式(27)表明,转子d、q轴电压除受到id、iq的控制以外,还受到电流交叉耦合项,转子电压降以及定子磁链的影响。因此,要实现对d、q轴电流的有效控制,必须解除d、q轴电流间耦合和消除电网电压扰动。引入中间变量:
为了消除静差,引入积分环节。根据式(27),设计如下电流控制器:
式中,分别为转子d、q轴电流参考值,kirp、kiri分别为转子电流控制器的比例、积分系数(通常的控制中,d轴的比例和积分系数和q轴的比例和积分系数设为一样)。
将式(29)代入式(27)中,得到:
式(30)表明,通过引入电流交叉耦合项,转子电压降以及定子磁链前馈补偿,从而实现了d、q轴电流的解耦控制,有效提高了系统的动态控制性能。
通过式(30),可以得到基于定子磁链矢量定向控制的转子电流闭环控制框图,如图4所示。
为验证上述方法的有效性,仿真实验如下:
为了验证DFIG网侧、转子侧变流器的控制方法,搭建基于PLECS平台的2MW双馈异步风力发电系统的仿真分析系统,仿真系统参数如下:
①双馈异步发电机额定功率:PN=2MW,额定频率fN=50Hz,额定电压UN=680V,极对数np=2,同步转速n1=1500r/min,绕组折算系数K_sr=Ns/Nr=1/2.6,定子电阻Rs=0.022Ω,转子电子Rr=0.0018Ω,定子漏感Lls=0.12×10-3H,转子漏感Llr=0.05×10-3H,互感Lm=2.9×10-3H;②背靠背交流变流器:直流环节电容:C=53×10-3F,直流环节电压Vdc=1200V,当直流母线电压超过1296V时,直流保护装置投入工作,低于1200V时切出;变流器侧电感:Lc=1.82×10-3H,网侧电感:Lg=0.273×10-3H,并联电容:Cf=100×10-6F。开关频率fsw=5kHz;③变压器变比以及传输部分参数:定子端变压器采用Y△Y接法;传输线每单位长度参数:电阻为0.206Ω,自感为0.363×10-3H,互感为0.121×10-3H,对中性点电容为0.25×10-6F,耦合电容为0.083×10-6F。
仿真系统结构框图如图5所示。
仿真分为次同步状态、超同步状态以及次同步到超同步的过渡过程三个方面来验证DFIG的矢量控制策略。网侧变流器采用电网电压定向矢量控制(图3),转子侧变流器采用定子磁链定向矢量控制(图4)。
次同步运行状态仿真:
通过转速反馈,将DFIG发电机转速控制在nr=1350r/min,低于同步转速n1,可以得到DFIG运行转差率为s=0.1。图6到图8为DFIG次同步稳态运行时的仿真波形。图6所示为DFIG定、转子和总输出有功、无功功率。可以看出,发电机转子输出有功功率为-0.2×106W,即向电网吸收转差率功率s*PN,发电机定子向电网输出有功功率为2×106W,故DFIG总输出有功功率为1.8×106W。可以看出,发电机定、转子输出无功均为零,即工作在单位功率因数条件下。
图7所示为DFIG次同步运行稳态时,转子的电流与电压波形。可以看出,发电机转子电压与励磁电流的频率为5Hz,即为转差频率50s,与前文分析一致。
图8所示为DFIG次同步运行稳态时,定子输出的电流与电压波形。从图8(a)可以看出,发电机定子输出电压频率为50Hz,达到并网基本要求,相电压幅值为约为570V。
超同步运行状态仿真:
通过转速反馈控制环节,将风力发电机转速控制在nr=1650r/min,高于同步转速n1,可以得到DFIG运行转差率为s=-0.1。图9到图11为DFIG超同步稳态运行时的仿真波形。
图9所示为超同步稳态运行时DFIG定、转子和总输出有功、无功功率。从图9(a)可以看出,发电机转子输出有功功率为0.2×106W,即向电网输出转差率功率s*PN,发电机定子向电网输出有功功率约为1.8×106W,故DFIG总输出有功功率为2×106W。从图9(b)可以看出,发电机定、转子输出无功均为零,即工作在单位功率因数条件下。
图10所示为DFIG超同步运行稳态时,转子的电流与电压波形。可以看出,发电机转子电压与励磁电流的频率为5Hz,即为转差频率50s。与图7对比可以发现,超同步运行时电压与电流的相序与次同步运行时刚好相反,与前面的分析一致。图11所示为DFIG超同步运行稳态时,定子输出的电流与电压波形。从图11可以看出,发电机定子输出电压频率为50Hz,相电压幅值为约为570V,与图8对比发现,定子输出电压与电流相序并没有随着发电机运行状态的改变而改变,与次同步运行时的波形基本一致,达到并网要求。
次同步运行到超同步运行的过渡过程:
通过转速反馈,将发电机转速从1350r/min提高到1650r/min,即从次同步运行状态到超同步运行状态。图12到图15为DFIG过渡过程的仿真波形。
图12所示为过渡过程中DFIG定、转子和总输出的有功、无功功率。由前面的分析知,Pe=(1-s)Ps、Pr=-sPs,因此当转差率由正变为负时,转子从吸收有功功率逐步变到发出有功功率,总功率由小于定子功率变为大于定子功率。发电机定、转子输出无功均为零,即始终工作在单位功率因数条件下。
图13所示为过渡过程中DFIG转子电压与电流,可以发现在发电机转速逐渐增加的过程中,转子电压、电流频率逐渐减小;在A点处,达到同步转速,励磁电流为直流;随着转速继续升高,转子电压、电流频率逐渐增大,最后达到稳态,此时转子电压、电流相序已经与次同步时相反,运行在超同步状态。
图14所示为过渡过程中电网侧相电压、相电流与直流母线电压。电网侧电压为定子变压器的高压处(35kV),可以看出在电机运行状态的过渡过程中,电网侧电压基本不变,说明该过程基本对电网没有影响,由于转子由吸收功率变为发出功率,能量流动方向变化的过程中导致直流母线电压升高,达到直流保护装置的阈值时,释放直流母线电压,最终母线电压达到稳态1200V。图15所示为过渡过程中转子转速与转矩。通过转速控制,转子转速逐渐从141.3rad/s(1350r/s)增加到172.7rad/s(1650r/s),转子转矩由于是电磁阻转矩,故为负值,并且稳态绝对值随转速的增大而减小,与前面的分析一致。
本发明建立了DFIG网侧PWM变流器数学模型,推导了ABC坐标系下的网侧变流器微分方程,设计了基于d轴电网电压定向的网侧变流器控制算法,实现电流跟踪控制和逆变器直流母线电压控制。建立了转子侧变流器数学模型,推导了转子电流与定子磁链之间的数学关系式,设计了定子磁链定向的DFIG转子电流控制算法。在PLECS软件平台下搭建了2MW双馈异步发电机的仿真模型,对次同步状态、超同步状态,以及次同步到超同步状态之间的过渡过程进行了详细分析,仿真结果验证了理论分析的正确性。
本领域的普通技术人员将会意识到,这里所述的实施例是为了帮助读者理解本发明的原理,应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其他各种具体变形和组合,这些变形和组合仍然在本发明的保护范围内。
- 还没有人留言评论。精彩留言会获得点赞!