一种永磁同步电机控制系统PID参数寻优方法与流程
本发明属于永磁同步电机控制系统领域,具体涉及一种永磁同步电机控制系统PID参数优化方法。
背景技术:
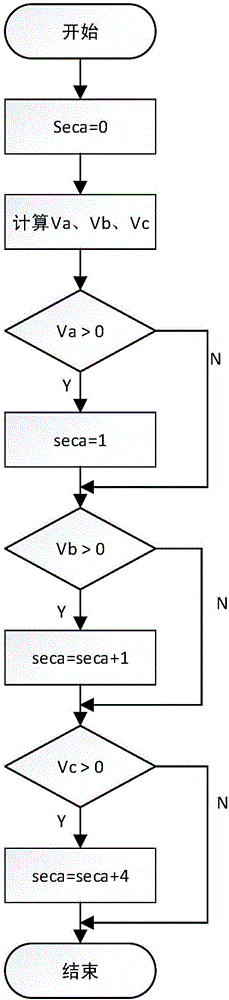
:永磁同步电机以其高能源利用效率、高力矩惯量比、高能量密度,环保低碳等特点,被广泛用于实现高精度和高效能的伺服控制系统。随着伺服控制系统的精度和性能要求的进一步提高,PID控制器成为实际电机控制系统中关键环节之一。PID控制器具有稳定性好、工作可靠、适应性好等诸多优点;但是,PID参数的整定一直是困扰工程人员的一个难题,一般都是根据系统特性和工程经验通过经验法采用实际反复试验进行PID参数整定;这种方法的缺陷在于:效率低、PID参数优化性能不佳,调试时间长,调试成本高,某些特殊系统伴随危险性,尤其无法适用一些高精准控制系统的参数调试。经验调试方法导致控制系统性能指标很难达到最优,并且很大程度上增加了控制系统的研发成本,延长了研发周期。技术实现要素:本发明提供一种永磁同步电机控制系统PID参数寻优方法,本发明是通过以下技术方案来实现的:一种永磁同步电机控制系统PID参数优化方法;包括以下几个步骤:步骤1:根据实际控制系统的内环电流环控制周期TC、外环速度环控制周期TS、晶振频率fosc、晶振周期Ts,计算仿真系统的仿真步长T1、电流环周期TC1和速度环周期TS1;步骤2:根据实际系统永磁同步电机的额定电流、额定转速,将电流环的电流反馈和电流环的速度反馈进行归一化计算;步骤3:CLARK变换;步骤4:PARK变换;步骤5:IPARK变换;步骤6:SVPWM设计;步骤7:使用matlab语言实现离散化的PID调节器;步骤8:建立控制系统参数评价函数;步骤9:采用Matlab语言设计遗传算法;步骤10:配置SIMULINK永磁同步电机和IGBT仿真模型参数;步骤11:构建永磁同步电机空间矢量算法SIMULINK仿真模型;步骤12:进行参数寻优,获取控制系统速度环和电流环PID优化参数。步骤1中具体分析及计算如下:由于控制系统本身的复杂度,以及执行机构的复杂度很高,一次仿真和计算的数据量特别大,这对于控制系统来说是不允许的,但是实际控制系统往往都具有一定的响应延时,控制系统响应时间往往较长,这就意味着仿真的时间必须较长才能看到控制效果;为了调节仿真系统和控制系统的矛盾,就必须对仿真系统中的仿真步长T1、电流环周期TC1和速度环周期TS1进行特殊设置;在实际应用中,实际控制系统有两个控制周期,包括内环电流环控制周期和外环速度环的控制周期,内环电流环控制周期TC=66us,外环速度环控制周期TS=264us,实际控制系统的晶振频率fosc=150MHz,实际控制系统的晶振周期Ts=6.6ns,实际控制系统的电流环的控制周期TC为10000×Ts=66us,实际控制系统的外环速度环周期TS为4倍的实际控制系统的内环电流环周期;考虑到如果将仿真系统的仿真步长T1设置为6.6ns,仿真系统的电流环控制周期和速度环控制周期和实际控制系统的电流环周期和控制环周期一样,会造成巨大的数据量,计算复杂,实际验证发现,一次系统仿真就会消耗半个小时,这样的仿真速度显然达不到我们的仿真需求。设置仿真系统中电流环的控制周期TC1为266us,速度环的控制周期TS1为1066us,仿真步长T1为0.5us,可以将仿真速度提高75倍;需要注意由于实际控制系统中的PID调节器中含有积分单元,实际控制系统中电流环周期为控制系统晶振周期的1000倍,仿真系统周期修改为控制系统晶振周期的133倍,这样的设置会导致PID调节器的不同,因此这里将PID调节器的积分参数与倍数相关联,避免了由于控制系统晶振周期调整而导致的调节器差异。步骤2的相关分析及计算如下:将关键变量进行归一化处理是在工程计算和电力系统中常用的一种数值标记方法,用来表示各物理参变量的相对值,简化运算过程,方便程序调试及纠错;归一化值=实际值/基准值,这个值是一种无量纲的量,一个物理量的归一化值在不同环境中是不固定的;这里进行归一化处理的变量有电流环的电流反馈和电流环的速度反馈;根据实际系统中电机的文档资料可以看出电机额定电流有效值为10A,设置电流标幺的基准值为10,电流环的电流反馈设置为10以内,实际控制系统中的电流经过AD采样后进行基准值为10的归一化处理,保证控制系统和仿真系统良好的对称性;实际控制系统中的永磁同步电机额定转速为3000RPM,设置电流环的速度反馈的基准值为3000,设置目标速度基准值为3000的归一化处理;经过以上的变量归一化处理,仿真系统的输入变量的范围设置在0~1之间,内部的坐标运算单元输入数据的范围设置在0~1之间,同样设置PID调节器的输出限幅为±1,就使得计算更加方便,易于进行计算和结果的分析比较。步骤3的相关分析及计算如下:永磁同步电机的控制系统中需要进行一系列坐标变换,在常规控制系统中,坐标变换可以通过程序实现也可以通过专业的芯片实现,这里仿真通过Simulink平台搭建,这些数学运算可以通过Matlab程序来实现。Clark变换将一个三相坐标系统变换到静止的两相α、β坐标系统中,从物理意义上讲,就是将电机ABC三相电压等效到另外一个静止坐标系中去,如公式(1)所示:VsαVsβ=10323VANVBN---(1)]]>其中,VAN、VBN分别指电机ABC三相中的AB两相的电压瞬时值,VSα、Vsβ分别指变换后的α、β坐标系统中的电压矢量值。步骤4的相关分析及计算如下:PARK变换同样是一个坐标变换,将静止的两相α、β坐标系统变换为一个转动的d、q轴坐标系统中,从物理意义上讲,就是结合步骤3中的坐标变换将电机三相电流投影、等效到d、q轴坐标系统中去,如公式(2)所示:uduq=cosθsinθ-sinθcosθuαuβ---(2)]]>其中,uα、uβ分别指步骤3中公式(1)通过CLARK变换得到的两相α、β坐标系统中的电压矢量,即VSα、Vsβ;这里的ud、uq分别指PARK变换后的d、q坐标系统中的电压矢量;步骤5的相关分析及计算如下:IPARK变换将转子的2轴电流矢量变换到定子的三相电流矢量中去,如公式(3)所示:uαuβ=cosθ-sinθsinθcosθuduq---(3)]]>步骤6:SVPWM设计,SVPWM是整个矢量控制的关键,具体包括以下几个步骤,步骤6.1:根据当前电机定子中的三相电流来确定矢量所处扇区seca,在进行矢量控制时,首先确定当前控制矢量的位置,再通过当前矢量位置控制指令确定下一时刻中电机三相线圈中的电流信号;考虑到算法比较复杂,在计算时包含很多中间计算过程,同时含有很多中间变量,其中Va、Vb、Vc就是其中的三个电压控制矢量中间变量;首先默认seca为0,根据步骤5中计算出的uα和uβ,计算电压控制矢量中间变量Va、Vb、Vc,计算公式如(4)所示:Va=UbetaVb=(-0.5*Ubeta+0.8660254*Ualpha)Vc=(-0.5*Ubeta-0.8660254*Ualpha)---(4)]]>式中,Ualpha和Ubeta分别对应公式(3)中的uα和uβ。然后将这三个电压控制矢量中间变量Va、Vb、Vc和0分别作比较,当Va>0时,seca置数为1,当Va≤0时,执行Vb>0的比较;当Vb>0时,在seca原有数值的基础上将加一,当Vb≤0时,执行Vc>0的比较;当Vc>0时,就在Vc原有数数值的基础上加4,当Vc≤0时,结束;步骤6.2:根据步骤6.1中扇区seca和电压控制矢量中间变量Va、Vb、Vc,确定电压控制矢量中间变量Va、Vb、Vc的作用时间Ta、Tb、Tc,矢量控制的核心就在于这部分,实质是一种对在三相正弦波中加入了两个零矢量的调制波进行规则采样的一种变形SPWM;SVPWM的调制过程是在空间实现的,没有明确的线电压调制波,SPWM是在ABC坐标系下分相实现的;根据步骤6.1中计算出的扇区位置信息,电压控制矢量中间变量Va、Vb、Vc,会有不同的作用时间Ta、Tb、Tc;根据扇区seca的数值,分别计算电压控制矢量中间变量Va、Vb、Vc的三个作用时间Ta、Tb、Tc;当seca=0时,根据公式(5)计算Ta、Tb、Tc时间,此时间即为三个作用时间Ta、Tb、Tc,且结束计算;当seca≠0时,执行seca=1,根据公式(5)计算Ta、Tb、Tc的时间,此时间即为三个作用时间Ta、Tb、Tc且结束计算;当seca≠1时,执行seca=2,此后依次按照SVPWM算法中的公式计算Ta、Tb、Tc的时间,此时间即为三个作用时间Ta、Tb、Tc;以此类推,执行到当seca=5时,计算Ta、Tb、Tc时间,结束;t1=Vct2=VbTb=0.5*(1.0-t1-t2)Ta=Tb+t1Tc=Ta+t2Ta=(Ta*NUB/8)Tb=(Tb*NUB/8)Tc=(Tc*NUB/8)---(5)]]>其中,NUB为速度环控制周期时间,t1、t2分别为两个中间变量;当seca为其它数值时,按照SVPWM的算法即可计算出时间Ta、Tb、Tc;其中SVPWM算法为现有算法,其中公式均可在相关资料中找到。步骤6.3:根据步骤6.2中计算出的三个作用时间Ta、Tb、Tc生成控制逆变器的六路PWM矢量控制信号;首先将三个作用时间Ta、Tb、Tc分别与一个三角波进行滞回比较,产生三路PWM矢量控制信号,然后将三路PWM矢量控制信号反相,又生成三路PWM矢量控制信号,共产生六路PWM矢量控制信号,六路PWM矢量控制信号分别为:U_true、U_false、V_true、V_false、W_true、W_false,其中六路PWM矢量控制信号分为三组,每组PWM矢量控制信号中的两个PWM矢量控制信号相反,作用于一组桥臂中的上下两个桥臂,从而,生成的六路PWM矢量控制信号分别作为逆变器的六个开关信号;通过这六路PWM矢量控制信号可以控制逆变器从而控制永磁同步电机。步骤7:使用matlab语言实现离散化的PID调节器;考虑到利用Matlab语言实现的PID调节器无法单独实现历史值的保存,所以利用Simulink中的Memory模块进行上一次历史值的保存,在下一次计算时将上一次历史值重新输入,在第一次PID计算时设置所有输入均为零,设置保存的变量有:历史误差(spd_old_SatErr)、历史输出(spd_old_Out)、历史输入(spd_old_Ui);具体为:首先更新控制系统周期,然后根据PID的计算公式来计算此时的PID输出值,对PID的输出值进行限幅操作,防止过大的控制信号所造成的控制系统不稳定现象,最后,将计算的中间变量和输出值进行保存,以便下一次的PID计算,至此,PID的参数离散化处理结束。步骤8:在对整个控制系统的控制效果进行评价时,常规的方法是观看电机的电流环响应、速度环响应以及转矩响应,直观的观看无法进行细致的效果评价,当单个参量调整后,无法具体量化和评价该参量改变后的控制效果变化;建立有效的控制系统参数评价函数,以此进行下一步控制参数优化和系统调整,具体的控制系统参数评价函数包含以下几个步骤:步骤8.1:控制系统中将转速作为主要性能指标,设置五个评价参数指标均与电机转速相关,设置暂态上升时间用来观察控制系统的快速机动能力;稳态上升时间可以评价系统的鲁棒性和稳定性;当电机转速稳定在目标转速的2%时即控制系统进入稳态;设置控制系统超调量和暂态振荡次数,用来评价整个控制系统的抗干扰情况;设置系统稳态误差,用来评价控制系统的稳态性能,当控制系统进入2%的稳态范围内后,会出现稳态震荡,这个震荡幅度是控制系统中一个非常重要的参数指标;步骤8.2:设置暂态上升时间(risetime)用Matlab语言实现;暂态上升时间是指从控制系统工作开始到实际电机转速为目标转速的95%时所消耗的时间;首先将暂态上升时间赋值为控制系统运行时间,按照时间从前往后的顺序进行顺序查询,实际转速是从0开始逐渐增加,此时判断转速是否到达目标转速95%的范围内,如果没有达到,保存当前时间点,继续判断,当实际转速到达目标转速95%的范围时,即确定此时的时间为暂态上升时间(risetime)。步骤8.3:设置超调量(overshot)用Matlab语言实现;超调量=(实际最大转速-目标转速)/目标转速×100%;首先将实际最大转速赋值为第一个速度采样值,然后依次时间顺序比较上一个时刻的速度采样值和当前时刻的速度采样值,在当前速度采样值大于上一时刻的速度采样值时,保存当前速度采样值,在当前速度采样值小于等于上一时刻的速度采样值时,继续时间顺序比较,通过顺序的迭代比较,最终找出最大的速度采样值,最后通过超调量公式计算出相应的超调量;步骤8.4:设置暂态振荡次数(oscnum)用Matlab语言实现,暂态振荡次数用来表示控制系统从暂态过渡到稳态时控制系统所经历的震荡状态,震荡的次数是评价整个控制系统设计和参数控制性能的最重要的一个指标;首先将暂态振荡次数赋值为0,然后,当控制系统进入暂态以后,依照时间顺序进行顺序查询,并判定此时的实际转速是否超出目标转速5%范围,如果实际转速超出目标转速的5%范围并回落一次,此时判断出系统响应出现一次震荡;如果实际转速未超出目标转速的5%范围,则继续时间顺序查询,这样通过在暂态范围内的反复判断,震荡次数累加,最终得到系统的暂态振荡次数;步骤8.5:设置稳态上升时间(transtime)用Matlab语言实现,稳态上升时间是指控制系统从启动开始,一直到控制系统达到稳态时所消耗的时间,当实际电机转速稳定在目标转速的±2%时,判断此时的时间为稳态上升时间;稳态上升时间不同于暂态上升时间反映电机的快速机动性,稳态上升时间可以评价系统的鲁棒性和稳定性,稳态上升时间这个参数的提高需要整个系统结构的高效设计以及敏感参量的调整优化;步骤8.6:设置稳态误差(stateerror)用Matlab语言实现;稳态误差代表了系统进入稳态后的振动情况,分布在整个频带,如果持续时间长或者较幅度较大的话,会降低整个系统的使用寿命,系统硬件的负载会增加,故障率会增加,系统可靠性降低;首先将稳态误差赋值为速度反馈的最大值,然后根据时间顺序从后往前查询,依次判断速度反馈是否超出目标转速的±2%,当速度反馈超出目标转速的±2%时,则上一个时刻的速度反馈即为系统稳态速度范围,这样就确定了系统整体的稳态速度范围,然后在这个稳态速度范围内,求得转速的平均值即为稳态转速均值,利用这个稳态转速均值和目标转速进行取绝对值的差值计算,再除以目标速度就获得了稳态误差;所述步骤8.3、步骤8.4、步骤8.5、须在控制系统达到稳态后才能计算,当控制系统未达不到稳态时,设置超调量和稳态误差均为1,设置暂态震荡次数为1,这样的设置覆盖了所有的控制系统响应,保证了系统参数评价函数在任何响应下均能对当前的系统状态做出最客观有效的评价,以便进行有效的系统及参量调整。步骤9:采用Matlab语言设计遗传算法;为了进一步挖掘仿真系统的价值,设计遗传算法利用仿真环境进行PID调节器的参数整定,采用现有成熟的遗传算法来进行参数整定可以节省大量的人力物力,有效提高系统研发效率,具体包括以下几个步骤:步骤9.1:遗传算法中的个体评价参数指标设置,遗传算法需要根据完善的个体评价参数指标设置来判断此个体的环境适应性,根据环境适应性来引导进行下一步的参数变异方向,缩小目标解范围,在步骤8中的五个评价参数指标,分别为暂态上升时间、稳态上升时间、暂态震荡次数、超调量、稳态误差,这时候没有确定的目标参数范围,参数寻优范围较大,寻优迭代次数多,加上暂态上升时间后,会导致响应畸形出现,在后期缩小目标参数范围后将暂态上升时间加入评价函数中去,使得变异方向更加准确;步骤9.2:遗传算法随着进化的进行,其选择率、交叉算子、变异率是动态改变的,通过分析系统要求,按照遗传算法的相关规则,确定遗传算法中一些具体参数的范围,比如种群中的个体个数,遗传率,变异等。步骤9.3:遗传算法中的一次参数寻优是在一个种群中进行的,种群的个数决定了最优解的范围以及染色体维度,当染色体维度很高时,遗传算法很难找到较好的解;考虑到最开始生成的初始种群适应度极其低,个体之间差异不大,对于染色体维度为10的数据,在进化初期靠在一个种群中交叉进行全局搜索来搜寻较优的个体,这里限定一个种群中的个体个数为50;步骤9.4:考虑到无法具体界定问题是否得到最优解,设置迭代次数为100;根据控制系统评价参数指标,选择速度的暂态震荡次数、超调量、暂态上升时间、稳态上升时间和稳态误差,根据这5个评价参数指标的加权平均,得到目标函数,考虑到应用遗传算法,因此最后的目标函数就会越来越收敛为0;因此,可以根据自己对参数具体的性能要求设置一个目标函数的范围,在一次次迭代时,判断每次参数的目标函数是否在这个范围内,如果在这个范围内,则停止迭代;步骤9.5:将步骤9.1中的5个评价参数指标按照一定的权重比相加,并且可以在寻优的不同时间分段修改各个参数的权重,以便达到最佳的寻优效果,设置上升时间的权重为0.1,设置超调量的权重为0.2,设置暂态震荡次数的权重为0.2,设置暂态上升时间和稳态上升时间的权重均为0.2,设置稳态误差的权重为0.3;以上五个评价参数指标按照各自权重比相加便得到寻优使用的目标函数;步骤9.6:终止条件设置为对目标函数的限制,经过几次不使用目标函数的仿真发现,最优的参数解出现时,此时的目标函数小于1,因此,设置寻优终止条件为目标函数小于1;步骤9.7:编写完整的遗传算法程序。步骤10:根据实际永磁同步电机和IGBT参数,配置SIMULINK永磁同步电机和IGBT仿真模型,实际控制系统中使用一款200W的永磁同步电机,仿真模型中的PMSM电动机设置和实际控制系统中永磁同步电机参数相同;仿真模型中的PMSM电动机相数设置为3相,反电动势类型设置为正弦,电动机转子类型设置为圆形,机械端输入设置为转矩输入;设置电动机定子电阻、电机定子电枢电感,电机定子绕组的永磁体磁链会自动设置,电压常数也被自动设置,设置电动机的转动惯量,设置电动机的粘滞阻尼,设置电动机的极对数,设置电动机的静摩擦系数;逆变器作为整个控制系统的关键环节,将母线电压转化为电机需要的三相电;设置桥臂数、电阻、电容为无穷大,根据实际系统的器件选择电力电子器件类型、导通电阻,分别设置正向电压,最后设置开通和关断时间。步骤11:利用步骤10中对逆变器和永磁同步电机的设置,完成步骤1到9的计算和设计,最终构建完整永磁同步电机空间矢量算法SIMULINK仿真模型,将各个模块相互关联设计为一个整体的控制系统,处理相关变量。步骤12:经过步骤9对遗传算法程序的设计,以及步骤11对控制系统仿真模型的设计,调用遗传算法,采用仿真算法进行参数寻优,设置迭代次数后,计算机开始寻优计算,计算结束后,可以获取控制系统最优速度环和电流环PID参数。与现有技术相比较,本发明的有益效果在于:(1)本发明基于一种永磁同步电机控制矢量控制策略,通过对电机、逆变器等器件进行精准的控制模型设计,对实际控制系统进行高相似度的仿真,设计出能够进行参数寻优的遗传算法,结合控制系统的仿真模型,寻优得到该控制系统的最优参数,从而提高控制系统自身的性能;(2)该方法可以针对实际应用中多数永磁同步电机和控制系统,进行参数寻优,而且,参数的性能明显优于利用工程经验调试的性能,有效挖掘了参数对系统的价值;(3)本发明克服了传统控制系统需要人工调试参数的缺点,降低了企业研发成本,有效提高了控制系统的研发速度、精度以及可靠性;(4)提高了永磁同步电机控制系统的开发效率,具有可观的社会效益和经济效益。附图说明图1是本发明的SVPWM扇区计算流程图;图2是本发明的空间矢量作用时间Ta、Tb、Tc计算流程图;图3是本发明PID控制算法流程图;图4是本发明暂态上升时间计算流程图;图5是本发明超调量计算流程图;图6是本发明暂态振荡次数计算流程图;图7是本发明稳态误差计算流程图;图8是本发明算法流程图;图9是本发明控制系统仿真模型图;图10是本发明模块结构图。具体实施方式具体实施例1:结合图1-图8,一种永磁同步电机控制系统PID参数优化方法;包括以下几个步骤:步骤1:根据实际控制系统的内环电流环控制周期TC、外环速度环控制周期TS、晶振频率fosc、晶振周期Ts,计算仿真系统的仿真步长T1、电流环周期TC1和速度环周期TS1;步骤2:根据永磁同步电机额定电流、额定转速,进行归一化计算;步骤3:CLARK变换;步骤4:PARK变换;步骤5:IPARK变换;步骤6:SVPWM设计;步骤7:PID参数离散化处理;步骤8:建立控制系统参数评价函数;步骤9:遗传算法设计;步骤10:配置SIMULINK永磁同步电机和IGBT仿真模型参数;步骤11:构建永磁同步电机空间矢量算法SIMULINK仿真模型;步骤12:进行参数寻优,获取控制系统速度环和电流环PID优化参数。所述步骤1中具体分析及计算如下:由于控制系统本身的复杂度,以及执行机构的复杂度很高,一次仿真和计算的数据量特别大,这对于控制系统来说是不允许的,但是实际控制系统往往都具有一定的响应延时,控制系统响应时间往往较长,这就意味着仿真的时间必须较长才能看到控制效果;为了调节仿真系统和控制系统的矛盾,就必须对仿真系统中的仿真步长T1、电流环周期TC1和速度环周期TS1进行特殊设置;在实际应用中,实际控制系统有两个控制周期,包括内环电流环控制周期和外环速度环的控制周期,内环电流环控制周期TC=66us,外环速度环控制周期TS=264us,实际控制系统的晶振频率fosc=150MHz,实际控制系统的晶振周期Ts=6.6ns,实际控制系统的电流环的控制周期TC为10000×Ts=66us,实际控制系统的外环速度环周期TS为4倍的实际控制系统的内环电流环周期;考虑到如果将仿真系统的仿真步长T1设置为6.6ns,仿真系统的电流环控制周期和速度环控制周期和实际控制系统的电流环周期和控制环周期一样,会造成巨大的数据量,计算复杂,实际验证发现,一次系统仿真就会消耗半个小时,这样的仿真速度显然达不到我们的仿真需求。设置仿真系统中电流环的控制周期TC1为266us,速度环的控制周期TS1为1066us,仿真步长T1为0.5us,可以将仿真速度提高75倍;需要注意由于实际控制系统中的PID调节器中含有积分单元,实际控制系统中电流环周期为控制系统晶振周期的1000倍,仿真系统周期修改为控制系统晶振周期的133倍,这样的设置会导致PID调节器的不同,因此这里将PID调节器的积分参数与倍数相关联,避免了由于控制系统晶振周期调整而导致的调节器差异。步骤2的相关分析及计算如下:将关键变量进行归一化处理是在工程计算和电力系统中常用的一种数值标记方法,用来表示各物理参变量的相对值,简化运算过程,方便程序调试及纠错;归一化值=实际值/基准值,这个值是一种无量纲的量,一个物理量的归一化值在不同环境中是不固定的;这里进行归一化处理的变量有电流环的电流反馈和电流环的速度反馈;根据实际系统中电机的文档资料可以看出电机额定电流有效值为10A,设置电流标幺时的基准值为10,电流环的电流反馈设置为10以内,实际控制系统中的电流经过AD采样后进行基准值为10的归一化处理,保证控制系统和仿真系统良好的对称性;实际控制系统中的永磁同步电机额定转速为3000RPM,设置电流环的速度反馈的基准值为3000,设置目标速度基准值为3000的归一化处理;经过以上的变量归一化处理,仿真系统的输入变量的范围设置在0~1之间,内部的坐标运算单元输入数据的范围设置在0~1之间,同样设置PID调节器的输出限幅为±1,就使得计算更加方便,易于进行计算和结果的分析比较。步骤3的相关分析及计算如下:永磁同步电机的控制系统中需要进行一系列坐标变换,在常规控制系统中,坐标变换可以通过程序实现也可以通过专业的芯片实现,这里仿真通过Simulink平台搭建,这些数学运算可以通过Matlab程序来实现。Clark变换将一个三相坐标系统变换到静止的两相α、β坐标系统中,从物理意义上讲,就是将电机ABC三相电压等效到另外一个静止坐标系中去,如公式(1)所示:VsαVsβ=10323VANVBN---(1)]]>其中,VAN、VBN分别指电机ABC三相中的AB两相的电压瞬时值,VSα、Vsβ分别指变换后的α、β坐标系统中的电压矢量值。步骤4的相关分析及计算如下:PARK变换同样是一个坐标变换,将静止的两相α、β坐标系统变换为一个转动的d、q轴坐标系统中,从物理意义上讲,就是结合步骤3中的坐标变换将电机三相电流投影、等效到d、q轴坐标系统中去,如公式(2)所示:uduq=cosθsinθ-sinθcosθuαuβ---(2)]]>其中,uα、uβ分别指步骤3中公式(1)通过CLARK变换得到的两相α、β坐标系统中的电压矢量,即VSα、VSβ;这里的ud、uq分别指PARK变换后的d、q坐标系统中的电压矢量;步骤5的相关分析及计算如下:IPARK变换将转子的2轴电流矢量变换到定子的三相电流矢量中去,如公式(3)所示:uαuβ=cosθ-sinθsinθcosθuduq---(3)]]>步骤6:SVPWM设计,SVPWM是整个矢量控制的关键,具体包括以下几个步骤,步骤6.1:根据当前电机定子中的三相电流来确定矢量所处扇区seca,在进行矢量控制时,首先确定当前控制矢量的位置,再通过当前矢量位置控制指令确定下一时刻中电机三相线圈中的电流信号;考虑到算法比较复杂,在计算时包含很多中间计算过程,同时含有很多中间变量,其中Va、Vb、Vc就是其中的三个电压控制矢量中间变量;首先默认seca为0,根据步骤5中计算出的uα和uβ,计算电压控制矢量中间变量Va、Vb、Vc,计算公式如(4)所示:Va=UbetaVb=(-0.5*Ubeta+0.8660254*Ualpha)Vc=(-0.5*Ubeta-0.8660254*Ualpha)---(4)]]>式中,Ualpha和Ubeta分别对应公式(3)中的uα和uβ。然后将这三个电压控制矢量中间变量Va、Vb、Vc和0分别作比较,当Va>0时,seca置数为1,当Va≤0时,执行Vb>0的比较;当Vb>0时,在seca原有数值的基础上将加一,当Vb≤0时,执行Vc>0的比较;当Vc>0时,就在Vc原有数数值的基础上加4,当Vc≤0时,结束;步骤6.2:根据步骤6.1中扇区seca和电压控制矢量中间变量Va、Vb、Vc,确定电压控制矢量中间变量Va、Vb、Vc的作用时间Ta、Tb、Tc,矢量控制的核心就在于这部分,实质是一种对在三相正弦波中加入了两个零矢量的调制波进行规则采样的一种变形SPWM;SVPWM的调制过程是在空间实现的,没有明确的线电压调制波,SPWM是在ABC坐标系下分相实现的;根据步骤6.1中计算出的扇区位置信息,电压控制矢量中间变量Va、Vb、Vc,会有不同的作用时间Ta、Tb、Tc;根据扇区seca的数值,分别计算电压控制矢量中间变量Va、Vb、Vc的三个作用时间Ta、Tb、Tc;当seca=0时,根据公式(5)计算Ta、Tb、Tc时间,此时间即为三个作用时间Ta、Tb、Tc,且结束计算;当seca≠0时,执行seca=1,根据公式(5)计算Ta、Tb、Tc的时间,此时间即为三个作用时间Ta、Tb、Tc且结束计算;当seca≠1时,执行seca=2,计算Ta、Tb、Tc的时间,此时间即为三个作用时间Ta、Tb、Tc且结束计算;以此类推,执行到当seca=5时,计算Ta、Tb、Tc时间,结束;t1=Vct2=VbTb=0.5*(1.0-t1-t2)Ta=Tb+t1Tc=Ta+t2Ta=(Ta*NUB/8)Tb=(Tb*NUB/8)Tc=(Tc*NUB/8)---(5)]]>其中,NUB为速度环控制周期时间,t1、t2分别为两个中间变量;当seca为其它数值时,按照SVPWM的算法即可计算出时间Ta、Tb、Tc;其中SVPWM算法为现有算法,其中公式均可在相关资料中找到。步骤6.3:根据步骤6.2中计算出的三个作用时间Ta、Tb、Tc生成控制逆变器的六路PWM矢量控制信号;首先将三个作用时间Ta、Tb、Tc分别与一个三角波进行滞回比较,产生三路PWM矢量控制信号,然后将三路PWM矢量控制信号反相,又生成三路PWM矢量控制信号,共产生六路PWM矢量控制信号,六路PWM矢量控制信号分别为:U_true、U_false、V_true、V_false、W_true、W_false,其中六路PWM矢量控制信号分为三组,每组PWM矢量控制信号中的两个PWM矢量控制信号相反,作用于一组桥臂中的上下两个桥臂,从而,生成的六路PWM矢量控制信号分别作为逆变器的六个开关信号;通过这六路PWM矢量控制信号可以控制逆变器从而控制永磁同步电机。步骤7的具体分析如下:使用matlab语言实现离散化的PID调节器;考虑到利用Matlab语言实现的PID调节器无法单独实现历史值的保存,所以利用Simulink中的Memory模块进行上一次历史值的保存,在下一次计算时将上一次历史值重新输入,在第一次PID计算时设置所有输入均为零,设置保存的变量有:历史误差(spd_old_SatErr)、历史输出(spd_old_Out)、历史输入(spd_old_Ui);具体为:首先更新控制系统周期,然后根据PID的计算公式来计算此时的PID输出值,对PID的输出值进行限幅操作,防止过大的控制信号所造成的控制系统不稳定现象,最后,将计算的中间变量和输出值进行保存,以便下一次的PID计算,至此,PID的参数离散化处理结束。所述步骤8:在对整个控制系统的控制效果进行评价时,常规的方法是观看电机的电流环响应、速度环响应以及转矩响应,直观的观看无法进行细致的效果评价,当单个参量调整后,无法具体量化和评价该参量改变后的控制效果变化;建立有效的控制系统参数评价函数,以此进行下一步控制参数优化和系统调整,具体的控制系统参数评价函数包含以下几个步骤:步骤8.1:控制系统中将转速作为主要性能指标,设置五个评价参数指标均与电机转速相关,设置暂态上升时间用来观察控制系统的快速机动能力;稳态上升时间可以评价系统的鲁棒性和稳定性;当电机转速稳定在目标转速的2%时即控制系统进入稳态;设置控制系统超调量和暂态振荡次数,用来评价整个控制系统的抗干扰情况;设置系统稳态误差,用来评价控制系统的稳态性能,当控制系统进入2%的稳态范围内后,会出现稳态震荡,这个震荡幅度是控制系统中一个非常重要的参数指标;步骤8.2:设置暂态上升时间(risetime)用Matlab语言实现;暂态上升时间是指从控制系统工作开始到实际电机转速为目标转速的95%时所消耗的时间;首先将暂态上升时间赋值为控制系统运行时间,按照时间从前往后的顺序进行顺序查询,实际转速是从0开始逐渐增加,此时判断转速是否到达目标转速95%的范围内,如果没有达到,保存当前时间点,继续判断,当实际转速到达目标转速95%的范围时,即确定此时的时间为暂态上升时间(risetime)。步骤8.3:设置超调量(overshot)用Matlab语言实现;超调量=(实际最大转速-目标转速)/目标转速×100%;首先将实际最大转速赋值为第一个速度采样值,然后依次时间顺序比较上一个时刻的速度采样值和当前时刻的速度采样值,在当前速度采样值大于上一时刻的速度采样值时,保存当前速度采样值,在当前速度采样值小于等于上一时刻的速度采样值时,继续时间顺序比较,通过顺序的迭代比较,最终找出最大的速度采样值,最后通过超调量公式计算出相应的超调量;步骤8.4:设置暂态振荡次数(oscnum)用Matlab语言实现,暂态振荡次数用来表示控制系统从暂态过渡到稳态时控制系统所经历的震荡状态,震荡的次数是评价整个控制系统设计和参数控制性能的最重要的一个指标;首先将暂态振荡次数赋值为0,然后,当控制系统进入暂态以后,依照时间顺序进行顺序查询,并判定此时的实际转速是否超出目标转速5%范围,如果实际转速超出目标转速的5%范围并回落一次,此时判断出系统响应出现一次震荡;如果实际转速未超出目标转速的5%范围,则继续时间顺序查询,这样通过在暂态范围内的反复判断,震荡次数累加,最终得到系统的暂态振荡次数;步骤8.5:设置稳态上升时间(transtime)用Matlab语言实现,稳态上升时间是指控制系统从启动开始,一直到控制系统达到稳态时所消耗的时间,当实际电机转速稳定在目标转速的±2%时,判断此时的时间为稳态上升时间;稳态上升时间不同于暂态上升时间反映电机的快速机动性,稳态上升时间可以评价系统的鲁棒性和稳定性,稳态上升时间这个参数的提高需要整个系统结构的高效设计以及敏感参量的调整优化;步骤8.6:设置稳态误差(stateerror)用Matlab语言实现;稳态误差代表了系统进入稳态后的振动情况,分布在整个频带,如果持续时间长或者较幅度较大的话,会降低整个系统的使用寿命,系统硬件的负载会增加,故障率会增加,系统可靠性降低;首先将稳态误差赋值为速度反馈的最大值,然后根据时间顺序从后往前查询,依次判断速度反馈是否超出目标转速的±2%,当速度反馈超出目标转速的±2%时,则上一个时刻的速度反馈即为系统稳态速度范围,这样就确定了系统整体的稳态速度范围,然后在这个稳态速度范围内,求得转速的平均值即为稳态转速均值,利用这个稳态转速均值和目标转速进行取绝对值的差值计算,再除以目标速度就获得了稳态误差;所述步骤8.3、步骤8.4、步骤8.5、须在控制系统达到稳态后才能计算,当控制系统未达不到稳态时,设置超调量和稳态误差均为1,设置暂态震荡次数为1,这样的设置覆盖了所有的控制系统响应,保证了系统参数评价函数在任何响应下均能对当前的系统状态做出最客观有效的评价,以便进行有效的系统及参量调整。步骤9:采用Matlab语言设计遗传算法;为了进一步挖掘仿真系统的价值,设计遗传算法利用仿真环境进行PID调节器的参数整定,采用现有成熟的遗传算法来进行参数整定可以节省大量的人力物力,有效提高系统研发效率,具体包括以下几个步骤:步骤9.1:遗传算法中的个体评价参数指标设置遗传算法需要根据完善的个体评价参数指标设置来判断此个体的环境适应性,根据环境适应性来引导进行下一步的参数变异方向,缩小目标解的范围,在步骤8中的五个评价参数指标,分别为暂态上升时间、稳态上升时间、暂态震荡次数、超调量、稳态误差,这时候没有确定的目标参数范围,参数寻优范围较大,寻优迭代次数多,加上暂态上升时间后,会导致响应畸形出现,在后期缩小目标参数范围后将暂态上升时间加入评价函数中去,使得变异方向更加准确;步骤9.2:遗传算法随着进化的进行,其选择率、交叉算子、变异率是动态改变的,通过分析系统要求,按照遗传算法的相关规则,确定遗传算法中一些具体参数的范围,比如种群中的个体个数,遗传率,变异等。步骤9.3:遗传算法中的一次参数寻优是在一个种群中进行的,种群的个数决定了最优解的范围以及染色体维度,当染色体维度很高时,遗传算法很难找到较好的解;考虑到最开始生成的初始种群适应度极其低,个体之间差异不大,对于染色体维度为10的数据,在进化初期靠在一个种群中交叉进行全局搜索来搜寻较优的个体,这里限定一个种群中的个体个数为50;步骤9.4:考虑到无法具体界定问题是否得到最优解,设置迭代次数为100;根据控制系统评价参数指标,选择速度的暂态震荡次数、超调量、暂态上升时间、稳态上升时间和稳态误差,根据这5个评价参数指标的加权平均,得到目标函数,考虑到应用遗传算法,因此最后的目标函数就会越来越收敛为0;因此,可以根据自己对参数具体的性能要求设置一个目标函数的范围,在一次次迭代时,判断每次参数的目标函数是否在这个范围内,如果在这个范围内,则停止迭代;步骤9.5:将步骤9.1中的5个评价参数指标按照一定的权重比相加,并且可以在寻优的不同时间分段修改各个参数的权重,以便达到最佳的寻优效果,设置上升时间的权重为0.1,设置超调量的权重为0.2,设置暂态震荡次数的权重为0.2,设置暂态上升时间和稳态上升时间的权重均为0.2,设置稳态误差的权重为0.3;以上五个评价参数指标按照各自权重比相加便得到寻优使用的目标函数;步骤9.6:终止条件设置为对目标函数的限制,经过几次不使用目标函数的仿真发现,最优的参数解出现时,此时的目标函数小于1,因此,设置寻优终止条件为目标函数小于1;步骤9.7:编写完整的遗传算法程序。所述步骤10:根据实际永磁同步电机和IGBT参数,配置SIMULINK永磁同步电机和IGBT仿真模型,实际控制系统中使用一款200W的永磁同步电机,仿真模型中的PMSM电动机设置和实际控制系统中永磁同步电机参数相同;仿真模型中的PMSM电动机相数设置为3相,反电动势类型设置为正弦,电动机转子类型设置为圆形,机械端输入设置为转矩输入;设置电动机定子电阻、电机定子电枢电感,电机定子绕组的永磁体磁链会自动设置,电压常数也被自动设置,设置电动机的转动惯量,设置电动机的粘滞阻尼,设置电动机的极对数,设置电动机的静摩擦系数;逆变器作为整个控制系统的关键环节,将母线电压转化为电机需要的三相电;设置桥臂数、电阻、电容为无穷大,根据实际系统的器件选择电力电子器件类型、导通电阻,分别设置正向电压,最后设置开通和关断时间。所述步骤11:利用步骤10中对逆变器和永磁同步电机的设置,完成步骤1到9的计算和设计,最终构建完整永磁同步电机空间矢量算法SIMULINK仿真模型,将各个模块相互关联设计为一个整体的控制系统,处理相关变量。步骤12:经过步骤9对遗传算法程序的设计,以及步骤11对控制系统仿真模型的设计,调用遗传算法,采用仿真算法进行参数寻优,设置迭代次数后,计算机开始寻优计算,计算结束后,可以获取控制系统最优速度环和电流环PID参数。结合图8为本发明的程序流程图,由于本发明中永磁同步电机的控制策略采用的是矢量控制策略;在程序开始之后,首先定义并进行说明,然后计算控制周期,接着进行相应的速度环、电流环的入口参数加载及计算,接着判定是否到达速度控制周期,如果到达速度控制周期,则进行反馈速度的计算,具体包括速度PID的计算,接着进行PID调节器的数据更新输出;如果没有到达控制周期,则输出上次更新值。接着进行电流环的控制周期计算,如果时间够一个周期,则进行相应的计算和控制量的输出,包括一些坐标变换和SVPWM的扇区计算,最后计算出三个控制时间信号Ta、Tb、Tc。如果此时没有到达电流的控制周期,则输出上次的更新值;根据电流环的输出更新或者输出保持,这样就得到了此时的三个控制时间Ta、Tb、Tc,接着进行六路PWM信号的计算输出,六路控制信号直接作用于逆变器的六个桥臂;最后进行基础的时钟更新,至此整个流程结束。结合图9为本发明中永磁同步电机控制系统的模型仿真图,整个控制系统模型建立在Matlab8.5/Simulink环境下,图中包含有永磁同步电机,逆变器,核心控制程序模块,示波器等模块。结合图10为本发明的模块结构图,从图中可以看出,本发明主要包含两部分内容,遗传算法模块和电机控制系统模型,遗传算法模块主要包含对速度信号的响应与处理和控制参数寻优算法两部分,电机控制系统模型即为图9的模型。具体实施例2:具体实施例2:本发明基于一种永磁同步电机控制系统PID参数优化方法,用户可以根据自己的控制系统的电机、逆变器设置仿真环境中的器件,根据自己控制程序中的相关配置,设置仿真系统中的相关配置选项,同时修改相关的参数范围,接下来就可以使用本发明来进行控制参数的整定与寻优,最后将仿真环境中的参数配置应用到自己实际的控制系统中去。仿真环境配置及设置如下:Windows10x64操作系统;Intel(R)Core(TM)i5-3230M处理器为;8G内存;仿真软件使用MathWorks公司的Matlab8.5,包含其中的Simulink模块。实际控制系统配置如下:基于DSP的主控制电路,大功率电源模块,基于IGBT的逆变电路模块,高精度电流采集传感器,上位机软件。用户在建立了实际的永磁同步电机控制系统后,根据实际永磁同步电机控制系统的特征对仿真系统进行设置便可以进行参数寻优操作,按照如下操作步骤进行便可:步骤A:查看实际永磁同步电机控制系统的具体设置,确定仿真环境需求,具体的仿真环境需求包括需要得到的控制器参数,例如是否需要电流环的控制参数等。步骤B:根据永磁同步电机资料确定仿真环境中永磁同步电机参数;例如电机的额定电压、额定电流、额定功率、额定转矩、极对数、定子电阻和定子电感等详细的电机设计参数;通过这些参数,进而对控制系统模型中的电机模型进行设置。步骤C:根据实际永磁同步电机系统中的逆变器资料确定仿真环境中的逆变器配置信息,具体包括导通电阻,上升时间,下降时间等参数信息。步骤D:检查永磁同步电机控制器中的程序设置,包括电流环控制周期、速度环控制周期,PID控制器类型,根据这些数据配置仿真环境中模块的输入采样频率,设置示波器的数据保存长度。步骤E:查看实际系统中电机相电流大小,AD采样设置,电机角度反馈等数据,对仿真系统进行标幺处理,标幺处理的数值根据实际情况而定,原则就是电流标幺的数值为电机相电流的额定数值,AD采样根据实际系统中的AD模块进行AD模块的位数设定,电机角度的反馈根据电机的极对数的不同,配置不同的机械角到电角度的变换关系。步骤F:根据实际控制系统的需求,配置遗传算法中的个体个数,染色体个数,迭代次数,其中的具体个数根据控制系统和寻优参数的不同会有很大差异,具体的数值可以参考成熟遗传算法中的具体设置。步骤G:根据实际永磁同步电机系统确定寻优参数的最优解范围,这个范围属于用户自定义的一个范围,由于不同控制系统的性能要求不同,没有统一的范围要求,即如果用户确定此控制系统最终所需参数的具体指标,计算出响应的控制系统性能范围,若这个范围可以确定,则跳至步骤I,否则继续步骤H。步骤H:如果不能确定寻优参数的最优解范围,在遗传算法程序中设置目标参数范围,这些参数的范围没有一个统一的限定,因为每个系统的PID参数都有很大差异,用户可以通过自己控制系统的特征来进行相应的参数范围设定;区间设置较大,则目标参数范围较大,设置遗传算法中的迭代次数大于150次,不设终止条件。步骤I:如果可以确定目标参数的最优解范围,则根据这个范围设置种群的范围一般范围可以设定为50,但是用户最好根据成熟遗传算法的相关设定来设置种群的范围,注意这个范围的设定一定得非常准确,否则会造成后边的参数寻优失败;步骤J:根据自己需求设计参数的响应指标:包括暂态上升时间,暂态振荡次数,稳态调节时间,超调量,稳态误差这些参数,包括目标解的范围,如果目标参数的范围可估计,则这个值也可大致估计。步骤K:根据步骤J确定的目标范围和各个性能指标设计寻优终止条件。经过这些步骤的设置,整个仿真环境的设计就基本结束,如果条件允许,下一步可以使用针对实际控制系统控制效果较好的参数,运用到仿真系统中去,以此检验仿真系统的可靠性。步骤L:启动遗传算法,开始参数寻优。步骤M:当寻优结束后,查看目标函数经过屡次迭代后的变化趋势,如果目标解收敛并且变得很小,则寻优成功,将目标参数运用至实际系统即可;如果参数不符合预期,则返回检查步骤H或者步骤I,重新开始寻优即可。表1环境设置具体设置仿真步长5.00E-07仿真时间0.4s求解器类型Fixedstep输出数据限制800000数据类型double系统采样时间inherited遗传算法设置具体设置种群个体个数50染色体个数10迭代次数150速度环P值范围0到1速度环D值范围0到100电流环P值范围0到10电流环D值范围0到100示波器数据限制不限制电动机设置具体设置Numberofphases3BackEMFwaveformSinusoidalRotortypeRoundMechanicalinputTorqueTmStatorphaseresistanceRs(ohm)0.2StatorphaseInductanceLs(H)0.0045MachineconstantTorqueConstant(N.m/A_peak)Inertia(J(kg.m^2)0.00001814viscousdamping(F(N.m.s))0.0002024polepairs4staticfriction(F(N.m))0Rotorfluxpositionwhentheta=0originalPark表1中包含所有的环境设置,其中设置范围为具体实施例中根据依次步骤得到具体设置。表2表2为两台电机的具体参数。表3表3寻优参数及性能比较,表3为利用表2中的两台电机在实际系统中的参数测试结果,其中A型电机的环境设定为表1所示,B型电机的环境设定根据juice实施例设定即可;其中的经验法参数为工程人员利用经验调试出的PID参数,寻优法为利用本发明方法得到的PID参数,测试转速设置为1000RPM;除此之外表3寻优参数及性能比较统计了经验法和寻优法在实际系统中的试验性能,结果表明,寻优法得到的参数在实际试验中的效果明显优于经验参数的效果,进一步证明了本发明的价值和实用性。当前第1页1 2 3
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1