一种基于坐标变换的电力系统短路电流衰减计算方法与流程
本发明涉及一种短路电流获取方法,尤其是涉及一种基于坐标变换的电力系统短路电流衰减计算方法。
背景技术:
目前,国内电力企业采用的常规短路电流计算只是计算短路电流周期分量,不能计算短路电流周期分量的衰减情况,而传统上采用的短路电流计算曲线法虽然能够计算短路电流周期分量的衰减情况,但是该方法将负荷等效为静态负荷,使用事先规定的电力系统典型运行方式而不是实际运行状态。
电网企业常用的商业电力系统仿真软件计算短路电流时,PSASP忽略负荷的影响;BPA程序可以考虑含有感应电动机的综合负荷,但是只能计算周期分量初始有效值;PSS/E的BKDY模块虽然能够计算短路电流周期分量的衰减情况,但是该方法将负荷等效为静态负荷,上述仿真软件的暂态稳定计算功能通过求解整个系统的微分方程,能够计算周期分量的衰减,然而数据准备繁琐、计算量偏大,一般不用于短路电流的工程计算。
技术实现要素:
本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种考虑全面、计算准确、贴近实际的基于坐标变换的电力系统短路电流衰减计算方法。
本发明的目的可以通过以下技术方案来实现:
一种基于坐标变换的电力系统短路电流衰减计算方法,包括以下步骤:
1)根据电网实际运行状态进行潮流计算,获取初始的节点电压方程,根据静态负荷和动态负荷的比例对初始的节点电压方程进行修正,得到修正后的节点电压方程;
2)对修正后的节点电压方程进行实数化表达,得到实数化后的节点电压方程;
3)根据实数化后的节点电压方程通过坐标变换获取旋转电机的网络方程,根据旋转电机的网络方程分别获取发电机和电动机对应节点的等值注入电流方程;
4)根据短路前的发电机和电动机电势以及旋转电机定子电流的计算方程分别获取发电机和电动机的衰减电势;
5)根据发电机和电动机的衰减电势、对应节点的等值注入电流方程计算各个节点的短路电压;
6)根据短路节点的节点电压及其相邻节点的短路电压获取短路节点的短路电流。
所述的修正后的节点电压方程为:
Ykk=YNkk+yLD.k
其中,为节点注入电流列向量,为节点电压列向量,Y为节点导纳矩阵,Ykk为节点导纳矩阵Y在节点k的自导纳,YNkk为修正前的节点导纳矩阵YN在节点k的自导纳,yLD.k为节点k的静态负荷等效导纳。
所述的实数化后的节点电压方程为:
其中,i,j为不同的母线节点编号,Gij、Bij分别为修正后的导纳矩阵Y中非对角元素的实部和虚部,Vjx、Vjy分别为节点j的节点电压复数形式的实部和虚部,I′ix、I′iy分别为节点i的节点注入电流复数形式的实部和虚部,n为母线节点总数;
所述的步骤3)中,旋转电机的网络方程的表达式为:
其中,I″ix、I″iy分别为旋转电机节点i等值注入电流复数形式的实部和虚部,Gix、Giy、Bix、Biy分别为旋转电机节点i的自导纳二阶子矩阵修正系数,Gij和Bij分别为节点导纳矩阵Y中非对角线元素的实部和虚部,Gii、Bii分别为节点导纳矩阵Y中对角线元素的实部和虚部,Vjx、Vjy分别为节点j的节点电压复数形式的实部和虚部。
当旋转电机为发电机时,其网络方程表达式与旋转电机的网络方程的表达式相同,式中:
其中,Ria、Xiq、X″id、X″iq分别为节点i所连发电机的内阻、q轴稳态电抗以及d、q轴次暂态电抗,Vi,δiV分别为节点i所连发电机的节点电压有效值和相位角,ΔVi、δV分别为发电机电压降落的纵分量和横分量,Pi、Qi为发电机向系统供给的有功功率和无功功率,δi为发电机转子q轴与x轴的夹角;
则有,发电机对应节点的等值注入电流方程为:
其中,I″ix、I″iy分别为发电机节点i等值注入电流复数形式的实部和虚部,E″iq、E″id为节点i所连发电机q、d轴次暂态电势,Cix1、Cix2、Ciy1、Ciy2为网络方程参数,Ria为节点i所连发电机的内阻,δi为发电机转子q轴与x轴的夹角,X″id、X″iq分别为节点i所连发电机的d、q轴次暂态电抗。
当旋转电机为电动机时,其网络方程表达式与旋转电机的网络方程的表达式相同,并且,
当电动机为双鼠笼感应电动机时,则有:
当电动机为单鼠笼感应电动机时,则有:
其中,Ria为节点i上的电动机内电阻,X′i为节点i上的电动机暂态电抗,ωi=1-si为电动机角速度,si为转差率。
当旋转电机为双鼠笼感应电动机时,其等值注入电流方程为:
ωi=1-si
其中,E″M-id、E″M-iq分别为节点i所连双鼠笼感应电动机d、q轴次暂态电势,Cix、Ciy为网络方程参数,Ria为节点i所连双鼠笼感应电动机的内阻,X′i为节点i所连双鼠笼感应电动机的电动机暂态电抗,ωi为双鼠笼感应电动机角速度,si为转差率;
当旋转电机为单鼠笼感应电动机时,其等值注入电流方程为:
ωi=1-si
其中,E′M-iq、E′M-id分别为节点i所连单鼠笼感应电动机的q、d轴暂态电势,Cix、Ciy为网络方程参数,Ria、X′i分别为节点i所连单鼠笼感应电动机的内阻、暂态电抗,ωi为单鼠笼感应电动机角速度,si为单鼠笼感应电动机转差率。
所述的步骤4)中,发电机衰减电势方程包括发电机短路d轴次暂态电势的衰减式和q轴次暂态电势的衰减式,
所述的发电机短路q轴次暂态电势的衰减式为:
其中,iid0为发电机短路前瞬间定子绕组d轴电流,Xid、X′id、X″id分别为发电机d轴的稳态电抗、暂态电抗和次暂态电抗,T′id、T″id为发电机d轴暂态分量和次暂态分量衰减的时间常数,Xie为发电机短路后瞬间发电机端电压与机端电流的比值,E″iq0为发电机短路前瞬间q轴暂态电势,E″iq为发电机短路后q轴暂态电势。
当发电机q轴方向有两个阻尼绕组时,所述的发电机短路d轴次暂态电势的衰减式为:
其中,iiq0为发电机短路前瞬间定子绕组q轴电流,Xiq、X′iq、X″iq分别为发电机q轴的稳态电抗、暂态电抗和次暂态电抗,T′iq、T″iq为发电机q轴暂态分量和次暂态分量衰减的时间常数,E″id为发电机短路后d轴暂态电势,E″id0为发电机短路前瞬间d轴暂态电势,
当发电机q轴方向只有一个阻尼绕组时,所述的发电机短路d轴次暂态电势的衰减式为:
所述的步骤4)中,电动机衰减电势方程包括双鼠笼感应电动机衰减电势方程和单鼠笼感应电动机衰减电势方程,
所述的双鼠笼感应电动机短路d轴次暂态电势的衰减式和q轴次暂态电势的衰减式为:
其中,iiq0、iid0分别为电动机短路前瞬间定子绕组q、d轴电流,Xiq、X′iq、X″iq分别为电动机q轴的稳态电抗、暂态电抗和次暂态电抗,Xid、X′id、X″id分别为电动机d轴的稳态电抗、暂态电抗和次暂态电抗,T′iq、T″iq为电动机q轴暂态分量和次暂态分量衰减的时间常数,T′id、T″id为电动机d轴暂态分量和次暂态分量衰减的时间常数,E″id、E″iq为电动机短路后d、q轴暂态电势,E″id0、E″iq0为电动机短路前瞬间d、q轴暂态电势,Xie为电动机短路后瞬间电动机端电压与机端电流的比值;
所述的单鼠笼感应电动机短路d轴次暂态电势的衰减式和q轴次暂态电势的衰减式为:
其中,E′iq、E′id和E′iq0、E′id0分别为电动机短路后和短路前瞬间d、q轴暂态电势。
所述的步骤4)具体包括以下步骤:
41)根据短路前的发电机、电动机电势获取旋转电机短路瞬间的等值注入电流;
42)根据短路瞬间的等值注入电流和实数化后的网络方程获取短路后瞬间各节点的电压;
43)根据短路前的各发电机和电动机的电势以及短路后瞬间各节点的电压获取各旋转电机短路后瞬间的注入电流,即旋转电机定子电流,所述的旋转电机定子电流的计算方程包括:
发电机定子电流方程:
双鼠笼感应电动机定子电流方程:
单鼠笼感应电动机定子电流方程:
其中,I′ix、I′iy分别为旋转电机定子电流复数形式的实部和虚部,Vix、Viy为旋转电机机端电压复数形式的实部和虚部,E″iq0、E″id0为旋转电机短路瞬间前的d、q轴暂态电势,Gix、Giy、Bix、Biy分别为旋转电机节点i的自导纳二阶子矩阵修正系数,Cix、Ciy为电动机网络方程参数,Cix1、Cix2、Ciy1、Ciy2为发电机网络方程参数;
44)根据短路后瞬间旋转电机的机端电压与注入电流计算该旋转电机与短路点间的电气距离Xie:
45)根据电气距离Xie、发电机和电动机的衰减电势方程获取旋转电机短路后的衰减电势。
所述的步骤6)中,短路节点的短路电流为:
其中,f为短路点,m为短路点支路数,为短路后与短路点f相连节点电压,Yif为短路点f与节点i的互导纳。
与现有技术相比,本发明具有以下优点:
本发明采用节点电压方程,利用坐标变换考虑各种发电机模型和动态负荷模型(动态负荷采用各种类型的感应电动机模型)计算对应节点的等值注入电流,最后通过求解网络方程(即节点电压方程)得到短路后各节点电压,进而计算短路电流衰减情况,与现有技术相比,本发明因为采用了d轴、q轴的分轴处理,可以考虑的发电机、感应电动机类型齐全,使考虑动态负荷影响后的系统短路电流衰减计算更接近实际情况。
这样短路电流的计算可以在考虑发电机、动态负荷贡献的同时计及短路电流的衰减,从而在选择电气设备和载流导体,整定继电保护装置,确定限制短路电流措施等方面做出更为准确的判断,保证设备安全的同时避免不必要的浪费。
附图说明
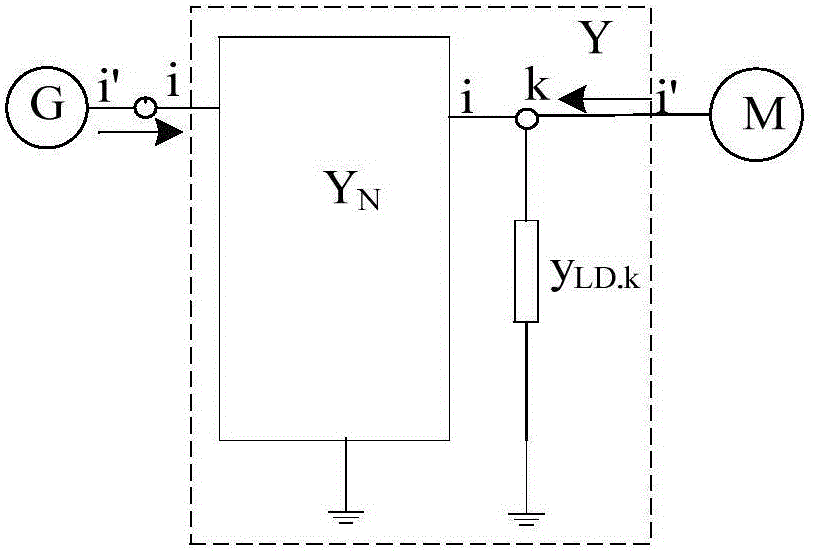
图1为发电机和负荷等值电路的接入图。
图2为坐标变换关系示意图。
图3为IEEE9系统的网络结构和短路前潮流分布。
图4为母线BusA三相短路时考虑动态负荷电流周期分量衰减示意图。
图5为母线BusA三相短路时静态负荷下电流周期分量衰减示意图。
图6为母线Bus1三相短路时考虑动态负荷电流周期分量衰减示意图。
图7为母线Bus1三相短路时静态负荷下电流周期分量衰减示意图。
具体实施方式
下面结合附图和具体实施例对本发明进行详细说明。
实施例:
本发明提出了一种利用坐标变换考虑电力系统运行状态影响的短路电流衰减实用计算方法。该方法采用节点电压方程,利用坐标变换,根据电力系统短路前的运行状态,计算节点电压方程中旋转电机对应节点注入电流,最后求解网络方程(即节点电压方程),进而计算短路电流衰减情况。
具体实施步骤及关键点如下:
(1)先根据电网实际运行状态进行潮流计算,得短路前潮流计算的节点电压方程如式(1),求解式(1)对应的潮流计算功率方程可得各节点电压和各支路功率;
(2)修正潮流计算的节点电压方程为式(2);
式(1)、(2)中为节点电压列向量;为节点注入电流列向量,前者的构成元素为图1中的i,后者的构成元素为图1中的i′;YN、Y为节点导纳矩阵,两者之间只有负荷节点对应的对角线元素(即负荷节点对应的自导纳元素)不同,后者在前者对应元素的基础上加图1中的yLD.k(即静态负荷对应的导纳),如图1所示。
(3)复数网络方程(节点电压方程)实数化表达
网络方程(2)中各向量参数写成复数表示可有Y=G+jB、对其进行实数化处理得任意节点i的方程矩阵形式如式(3)所示:
(4)用坐标变换求发电机对应节点的注入电流及网络方程
在用电力网络方程(3)计算衰减短路电流时,节点注入电流复向量只有发电机节点和电动机负荷节点的电流不为零,其余节点均为零。
对于节点i上的电机,首先将旋转电机d、q坐标系建立的电压平衡方程(电压电流正向采用发电机惯例)进行坐标变换(坐标间关系如图2所示),得到x、y坐标系下的旋转电机定子电流方程;然后代入x、y坐标系的实数化网络方程(3)进行合并得到网络方程(4):
图2中:其中Ria、Xid、Xiq分别为节点i上旋转电机的内电阻以及d、q轴稳态电抗,δiv为节点i上的电机机端电压的角度。
网络方程(4)的推导过程为:
发电机与电动机磁链公式都是分别在d、q轴坐标系下计算的。但是在系统中进行短路电流计算时必须是在统一的坐标系下,并且由于系统中电机的转子位置一般各不相同,因此需要在全系统中设置统一的坐标轴x、y,以便建立各电机d、q轴运行参数之间的联系。如果将同步旋转的参考轴选为与x轴重合,则电机转子q轴与x轴的夹角δ,即为转子的绝对角,从d、q坐标系到x、y坐标系的变换矩阵C如式(1-1)所示。
式中:其中Ra为旋转电机内电阻,Xq为旋转电机q轴稳态电抗,δV为电机机端电压的角度。
由此可得出x、y坐标系与d、q坐标系之间转换关系如式(1-2)所示。
计及发电机阻尼绕组影响时,计算发电机节点对电网的注入电流,须按固定在电机转子上的d、q坐标系建立电压平衡方程,其矩阵形式如下式所示。
对式(2-1)等号两边同乘以坐标变换的矩阵C,可得x、y坐标系下的发电机定子电流如式所示。
式中各参数如式(2-3)、(2-4)所示,
其中,RGa、X″Gd、X″Gd分别为节点i上旋转电机的内电阻以及d、q轴次稳态电抗。
根据实数化网络方程,可知如果节点i为发电机节点,则节点注入电流即为发电机定子电流,节点电压即为机端电压。将定子电流算式(2-2)代入实数化网络方程(3)左端,其中与机端电压有关的项移到右端与同类项合并,便可得到网络方程(2-5)
其中参数Gix、Giy、Bix、Biy与式(2-3)相同。
其中任意发电机节点注入电流I″i=I″ix+jI″iy可统一表示为如式(2-6)所示。
式中:E″id、E″iq分别为节点i上的发电机次暂态电势,其他四个参数如式(2-4)所示。
(5)用坐标变换求电动机对应节点的注入电流
为和同步发电机保持一致,将感应电动机机端电流正方向设置为发电机惯例,则网络方程(2-5)不仅适用于发电机,而且对于电动机同样适用,但其中的参数计算公式与发电机的不同。
对于双鼠笼感应电动机,对应(4)式,任意电动机节点的参数Gix、Giy、Bix、Biy可统一表示为如式(8)所示。其中,Ria为节点i上的电动机内电阻,X″i为节点i上的电动机次暂态电抗,ωi=1-si(s为转差率)。
同时式(4)中任意电动机节点注入电流可统一表示为如式(9)所示。
式中:E″id、E″iq分别为节点i上的电动机次暂态电势,其他四个参数如下式(10)所示。其中,Ria、X″i、ωi同式(8)。
对于单鼠笼感应电动机,对应(4)式,任意电动机节点的参数Gix、Giy、Bix、Biy可统一表示为如式(11)所示。其中,Ria为节点i上的电动机内电阻,X′i为节点i上的电动机暂态电抗。
同时式(4)中任意发电机节点注入电流可统一表示为如式(12)所示。
式中:E′id、E′iq分别为节点i上的电动机d、q暂态电势,其他四个参数如下式(13)所示。其中,Ria、X′i同式(11)。
(6)发电机衰减电势的计算
计算短路后任意时刻旋转电机的注入电流,由式(2-6)、式(9)及式(12)可知,首先需要计算出任意时刻的电机电势。
对于节点i上的发电机,其短路q轴次暂态电势的衰减计算如式(14)所示。
式中:iid0为发电机短路前瞬间定子绕组d轴电流;Xid、X′id、X″id分别为发电机的稳态电抗、暂态电抗、次暂态电抗;T′id、T″id分别为d轴暂态分量、次暂态分量衰减的时间常数;Xie为基于节点导纳矩阵计算的短路后瞬间发电机端电压与机端电流的商,E″iq0为q轴短路前瞬间次暂态电势。
对于d轴次暂态电势,当q轴有两个阻尼绕组时,其次暂态电势的衰减如式(15)所示。
式中:iiq0为发电机短路前瞬间定子绕组q轴电流;Xiq、X′iq、X″iq分别为发电机的稳态电抗、暂态电抗、次暂态电抗;T′iq、T″iq分别为q轴暂态分量、次暂态分量衰减的时间常数;Xie为基于节点导纳矩阵计算的短路后瞬间发电机端电压与机端电流的商;E″id0为d轴短路前瞬间次暂态电势。
而当发电机q轴方向只有一个阻尼绕组时,其d轴次暂态电势的衰减如式(16)所示。
式中参数同式(15)。
(7)电动机衰减电势的计算
对于节点i上的双鼠笼感应电动机,,短路后d、q轴暂态电势的衰减分别如式(17)、(18)所示。其中,E″iq0、E″id0分别为电动机短路瞬间d、q轴暂态电势,其他参数同式(14)。
对于节点i上的单鼠笼感应电动机,短路后d轴暂态电势的衰减如式(19)所示。其中,E′iq0为电动机短路瞬间d轴暂态电势,其他参数同式(14)。
(8)求解网络方程,计算短路后电压。
由电机衰减电势计算公式可以看出要计算电势首先需要在短路发生瞬间计算Xie的值。计算得到各旋转电机的注入电流后,可根据网络方程(3)求出电机机端电压Vix、Viy;并根据旋转电机定子电流方程(发电机如式(21)所示;双、单鼠笼电动机分别如式(22)、(23)所示)求出定子电流I′ix、I′iy。则旋转电机的参数Xie,计算公式如(24)所示。
这样,可根据衰减电势方程计算短路后任意Δt时刻的发电机电势与电动机电势,采用坐标变换计算任意Δt时刻注入电流,求解网络方程可得短路后任意Δt时刻电压。
(9)求解短路电流
在短路电流计算中,如果能够求出任意时刻发电机及动态负荷向电力网络的注入电流那么就可以利用网络方程式(2)求解电力网络得到利用与短路点相连节点电压和互导纳乘积,得短路点相连所有支路供给的短路电流,求和得总的短路电流。
根据上述计算过程求得任意时刻节点电压及注入电流,然后利用式(25)求出任意Δt时刻短路电流,即计算出短路电流衰减情况。
式中:f为短路点,m为短路点支路数,为短路后与短路点相连节点电压,Yif为短路点与节点i的互导纳。
另外,该计算方法在考虑动态负荷计算衰减短路电流时,需要将总负荷分出一部分作为动态负荷。对于有功部分,直接按照静态负荷与动态负荷的比例分为P0(静态负荷)和P(动态负荷),P0+P=PLD;而对于无功部分,要根据动态负荷对应的有功功率、负载率和电动机稳态等值电路,计算电动机对应的稳态无功部分Q,然后总的无功负荷QLD减去动态负荷需要的无功Q后剩余部分即为静态负荷的无功Q0,即Q0=QLD-Q,这样考虑动态负荷后的系统潮流与原来一致。
采用上述方法计算考虑动态负荷特性的短路电流衰减。该方法所得结果与计算曲线法的计算结果进行比较,并且用机电暂态仿真计算结果作为其合理性与正确性的判断。机电暂态仿真计算方法精确考虑了发电机的准稳态模型,通过发电机的微分方程和网络代数方程联立求解,所以其数据准备、建模较复杂,计算所需内存和运算量均较大,机电暂态仿真计算方法一般不作为短路电流常规计算方法,但其可以用来校核其他短路电流计算方法的准确性。
这里选择IEEE9系统作为本发明的应用举例,对母线BusA的负荷按照40%动态负荷+60%静态负荷的比例进行分配,其余负荷仍为静态负荷。分别对系统中母线BusA和母线Bus1进行考虑负荷动态特性的三相短路电流衰减计算,同时列出计算曲线法的计算结果作为对比。IEEE9系统的网络结构和短路前潮流分布如图3所示,计算结果如表1、表2和图4至图7所示。
表1考虑负荷动态特性前后短路电流周期分量衰减对比
表2考虑负荷动态特性前后短路电流周期分量衰减对比
从表1、表2和图4至图7可以看出,未考虑动态负荷时,实用计算法和机电暂态仿真结果总体上比较接近,具有较高的精确性。相比之下,传统计算曲线的计算结果更加保守,短路点不同,相差率也不同。如果短路发生在母线Bus1,相差率均大于10%;如果短路发生在母线BusA,相差率都在10%以内。因此如果用传统计算曲线的计算结果校核断路器的开断电流,仍有一定的安全裕度,但是在某些短路点(如本算例中的母线Bus1)显得过于保守,不利于挖掘断路器的开断潜力。
考虑负荷动态特性后,实用计算法与机电暂态仿真的计算在不同时刻具有较好的吻合度,在研究的时间范围0-0.1s内,相差率在±4%以内;并且在考虑负荷动态特性后,实用计算法计算所得的电动机增流效果非常显著,短路瞬间当短路点离动态负荷较近时增大率达到15%以上,随后逐渐减小,至0.1s减小到10%以内;当短路点离动态负荷较远时,其增大率达到5%以上,随后逐渐较小到1%以内,衰减情况符合理论规律。
通过应用举例分析,可以说明本发明提出的考虑动态负荷特性的短路电流衰减实用计算方法的计算结果具有较高的精确性,短路电流衰减曲线与机电暂态的吻合度也较好。因此能够用于考虑动态负荷的电网短路电流衰减特性研究,并且考虑动态负荷特性后较未考虑时所得结果更符合电网实际短路电流情况。
- 还没有人留言评论。精彩留言会获得点赞!