一种精确计算配电网支路阻抗的方法与流程

本发明涉及一种计算方法，具体讲涉及一种利用智能电表的量测数据精准计算配电网支路阻抗进而实现配电网精确建模的方法。
背景技术：
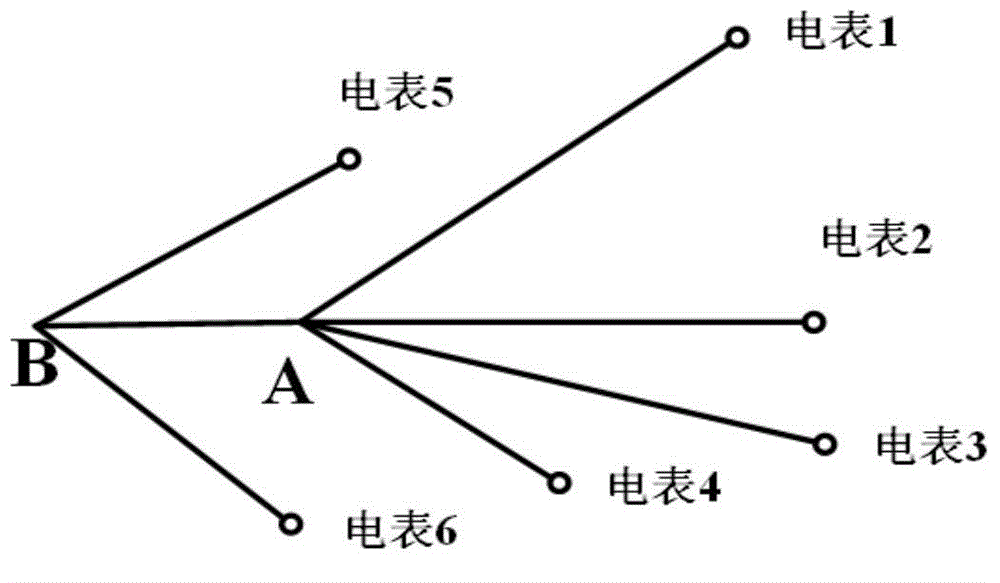
：高级量测体系(AMI)中的智能电表是一种可编程设备，可以实现包括电能消费记录在内的更多功能；同时，智能电表内置了通信模块，可以在双向通信系统中与数据中心的数据终端进行通信。通过智能电表得到的数据量是十分巨大，目前智能电表数据的有效利用主要表现在以下几个方面：1.使用高级量测体系(AMI)数据进行配网拓扑错误的校验。该算法的目的是运用智能电表数据进行检测和修正现有GIS系统中配电网的拓扑错误，最终形成正确的配网拓扑结构。2.利用台区变压器电压和智能电表电压进行相关性分析，以判断电表所属相位，并利用线性回归提升相位检测的准确性。根据这些结果，可以搭建仿真拓扑、实现虚拟电压量测，并可以进行窃电检测。3.对高级量测体系(AMI)的测量值在准实时高度精确的低压网络进行建模，建模所需数据是智能电表数据和66kV/22kV台区变压器电压数据。由于种种原因，目前有的配电网的拓扑(线路连接)和参数信息(线路类型，长度等)不够准确，特别是低压侧的二次系统，因此实现配电网的精确建模很困难，而目前高级量测体系(AMI)得到的数据尚未用于配电线路阻抗参数的精确计算以实现配电网的精确建模。技术实现要素：为了解决现有技术中所存在的上述不足，本发明提供一种精准计算配电网支路阻抗的方法，该方法结合已有的配电网拓扑结构，基于智能电表量测数据，精 确地计算出配电线路的阻抗参数，进而实现配电网的精确建模。本发明提供的技术方案是：一种精确计算配电网支路阻抗的方法，所述配电网包括树状连接的设有智能电表的节点；其改进之处在于：所述方法包括如下步骤：S1，设置所述配电网每条支路的电阻和电抗初值；S2，依次用时间间隔为i时所述配电网中每块智能电表数据、以及所述配电网支路电阻和电抗计算时间间隔为i时与每块智能电表数据相对应的所述配电网根节点的电压；S3，用下述公式(1)和公式(2)分别计算时间间隔为i时所述根节点电压的均值UR_ave(i)和方差UR_var(i)；UR_ave(i)=1nΣj=1nURj(i)---(1)]]>UR_var(i)=1nΣj=1n(URj(i)-UR_ave(i))2---(2)]]>式中：n——配电网中智能电表的总数；URj(i)——时间间隔为i时利用第j个智能电表的数据计算得到的配电网的根节点电压；S4，用公式(3)计算所述智能电表测量的所有时间间隔方差的均值UR_var_All；UR_var_All=1NΣi=1NUR_var(i)---(3)]]>其中N为智能电表测量的时间间隔的数量；S5，根据判断所述均值UR_var_All是否连续两次小于终止约束公差，且两次均值的差值小于差值阈值，确定进行步骤S6或步骤S7；S6当所述均值连续两次小于终止约束公差，且两次均值的差值小于差值阈值时，此时记录的所述配电网中每条支路的电阻和电抗为需要求取的配电网支路阻抗，计算结束；S7否则，根据梯度搜索算法改变所述配电网中每条支路的电阻和电抗，返 回步骤S2。优选的，所述终止约束公差的取值小于或等于0.0001，所述差值阈值取值小于或等于0.00001。优选的，所述步骤S2之前还包括：每隔时间间隔t采集所述配电网中每块智能电表测量的数据，共采集1～N次；所述智能电表测量的数据包括电压、有功功率和无功功率数据。优选的，所述步骤S2中计算与每个智能电表数据相对应的根节点电压时，除连接根节点的智能电表以外的智能电表，需根据节点的邻接关系，最先计算与连接叶子节点的智能电表数据相对应的根节点电压，逐级向上最后计算与连接根节点的子节点的智能电表数据相对应的根节点电压。进一步，所述步骤S2中，计算与每个智能电表数据相对应的根节点电压的步骤如下：A1，用下述公式(4)计算与智能电表连接的节点电压；UA=U12+1U12[(P12+Q12)R12+(P12+Q12)X12]+2P1R1+2Q1X1;---(4)]]>式中：U1——智能电表中的电压；UA——与该智能电表连接的节点电压；P1——智能电表中的有功功率；Q1——智能电表中的无功功率；R1——该节点到该智能电表的线路的电阻；X1——该节点到该智能电表的线路的电抗；A2，根据判断与智能电表连接的节点是否为根节点，确定进行步骤A3或步骤A7；A3，当与智能电表连接的节点不为根节点时，将与所述智能电表连接的节点作为子节点，转至步骤A4；A4，用公式(5)计算子节点的父节点电压；UB=UA2+1UA2[(PA2+QA2)RAB2+(PA2+QA2)XAB2]+2PARAB+2QAXAB---(5)]]>式中：UA——子节点的节点电压；UB——父节点的节点电压；RAB——父节点到子节点线路的电阻；XAB——父节点到子节点线路的电抗；PA——子节点的有功功率；QA——子节点的无功功率；A5，根据判断所述父节点是否为根节点，确定进行步骤A6或步骤A7；A6，当所述父节点不为根节点时，将所述父节点作为新的子节点，跳转至步骤A4；A7，否则，记录与智能电表数据相对应的根节点电压。进一步，用下式(6)和式(7)计算所述子节点的有功功率PA和无功功率QA：PA=Σj=1m(Pj+ΔPj)QA=Σj=1m(Qj+ΔQj)---(6)]]>ΔPj=Pj2+Qj2Uj2RjΔQj=Pj2+Q12Uj2Xj---(7)]]>其中m为该子节点的下游节点或下游支路的总数，Pj为该子节点的下游节点中的第j个下游节点的有功功率；ΔPj为该子节点的下游支路中第j条下游支路的有功功率损耗；Qj为该子节点的下游节点中的第j个下游节点的无功功率；ΔQj为该子节点的下游支路中第j条下游支路的无功功率损耗；Rj为该子节点的 下游支路中第j条下游支路的电阻；Xj为该子节点的下游支路中第j条下游支路的电抗；Uj为该子节点的下游节点中的第j个下游节点的节点电压；所述该子节点的下游节点包括与该子节点连接的智能电表、由该子节点所扩展而形成的树枝中除该子节点外的所有节点、以及连接所有节点的智能电表；所述下游支路包括树状结构中连接所述下游节点的支路。优选的，当所述配电网的根节点是变压器的二次侧出口时，测量所述根节点的电压UR_measured(i)，所述步骤S5中根据判断均值是否连续两次小于终止约束公差，且两次均值的差值小于差值阈值，确定进行所述步骤S6或所述步骤S7；其中：N——智能电表测量的时间间隔的数量；n——配电网中智能电表的总数；UR_measured(i)——时间间隔为i时所述根节点的电压测量值；URj(i)——时间间隔为i时利用第j个智能电表的数据计算得到的配电网的根节点电压。与最接近的技术方案相比，本发明具有如下显著进步：本发明提供的技术方案结合已有的配电网拓扑结构，基于高级量测体系(AMI)量测数据，能够精准地计算出配电网线路的阻抗参数，为实现配电网的精准建模奠定了技术基础。附图说明图1为简单的配电网网络拓扑图；图2为图1中A点电压和电表1的电压的向量关系图；图3为用于算例分析的真实配电网拓扑图；图4为两种情况下目标函数的收敛效果图；图5为用情况1计算得到的图3中A点电压UA误差；图6为用情况2计算得到的图3中A点电压UA误差。具体实施方式为了更好的理解本发明，下面结合说明书附图和实例对本发明的内容做进一步的说明。下面以如附图1所示的现有的闭环设计、开环运行的呈现辐射状的配电网为例，对本发明做详细说明，这种配电网通常包括树状连接的节点，每个节点均连接有一个或一个以上智能电表，假设4个智能电表1-4连接于节点A，节点A与智能电表5-6连接于节点B。这些智能电表均由同一变压器的一相供电，并且节点B是智能电表1-6的上游节点，其中：上游节点和下游节点之间的划分是相对的。在辐射状树形网络中，由一个节点所扩展而形成的树枝中除该节点外的所有节点和连接所有节点的智能电表、以及连接该节点的智能电表均成为该节点的下游节点，而该节点称为上游节点。配电网引入高级量测体系(AMI)后，我们可以得到智能电表处一定时间间隔的电压、有功功率和无功功率数据，节点A和节点B处的电压、有功功率和无功功率数据一般是无法直接测量的，但是当线路(智能电表到节点A、节点B之间的阻抗)的阻抗参数已知的情况下，可以利用电表的数据计算得到。基于此，我们采用下面的方法进行阻抗计算。对于从节点A到电表1的线路，根据欧姆定律：U·A-U·1=(R1+jX1)·I·1---(1)]]>式中：——节点A电压；——电表1的电压；——从节点A流向电表1的电流，R1——该段线路的电阻；X1——该段线路的电抗。以的方向为参考轴，得到如附图2的向量关系。在附图2中，将分解为与同方向的和与方向垂直的二者的大小为：式中：——与的夹角。电表1的功率可以表示为：式中：P1为电表1的有功功率，Q1为电表1的无功功率；在图2中，可以得到关于电压的等式：UA2＝(U1+ΔU1)2+δU12(6)联立式(2)至(6)，将电压、有功功率、无功功率和电阻、电抗写成如下方程UA2=U12+1U12[(P12+Q12)R12+(P12+Q12)X12]+2P1R1+2Q1X1---(7)]]>节点A与电表2、3、4之间的等式关系，以及节点B与电表5、6之间的等式关系，均可写成相似的方程。而从节点B到节点A的线路可以表示成与式(7)相似的形式：UB2=UA2+1UA2[(PA2+QA2)RAB2+(PA2+QA2)XAB2]+2PARAB+2QAXAB---(8)]]>式中：RAB——节点B到节点A线路的电阻；XAB——节点B到节点A线路的电抗。节点A的功率等于其下游节点的功率与线路损耗的总和：PA=Σj=1m(Pj+ΔPj)QA=Σj=1m(Qj+ΔQj)---(9)]]>ΔPj=Pj2+Qj2Uj2RjΔQj=Pj2+Q12Uj2Xj---(10)]]>式中：m——节点A的下游节点或下游支路的总数，Pj——节点A的下游节点中的第j个下游节点的有功功率；ΔPj——节点A的下游支路中第j条下游支路的有功功率损耗；Qj——节点A的下游节点中的第j个下游节点的无功功率；ΔQj——节点A的下游支路中第j条下游支路的无功功率损耗；Rj——节点A的下游支路中第j条下游支路的电阻；Xj——节点A的下游支路中第j条下游支路的电抗；Uj——节点A的下游节点中的第j个下游节点的节点电压；这里的下游支路指的是连接下游节点的支路。对于节点A，m为4。对于节点B的计算，节点A可以视作其下游的虚拟电表，m为7。基于上述公式，可以利用电表1数据计算得到UA，进而得到UB。当使用不同的电表数据时，可以得到不同的UB，并且其值在同一时间间隔内应该是相同的。这仅仅是考虑了一个时间间隔。AMI系统提供了大量的数据，确保了时间间隔的数量用于计算，并且在这些时间间隔中，线路的长度、参数是不变的。据此，可以计算电阻和电抗值。1)设置网络拓扑中每条支路的电阻和电抗初值。2)将电阻和电抗的值带入式(7)至(10)，利用不同的电表数据得到不同的 UB，记为UBm(m＝1,2,…)。假设节点B下游共有n个电表，那么得到的UB的数量为n(此处n为6)。3)计算这n个UB的平均值和方差：UB_ave=1nΣj=1nUBj---(11)]]>UB_var=1nΣj=1n(UBj-UB_ave)2---(12)]]>4)式(12)是一个时间间隔的方差。对于电表测量的所有时间间隔，最终所求的方差应是所有时间间隔方差的平均值：UB_var-ALL=1NΣi=1NUB_var(i)---(13)]]>其中，UB_Var(i)表示时间间隔i时计算的方差，N表示时间间隔的数量。5)根据梯度搜索算法改变电阻和电抗的值，返回步骤2)，直到UB_var-ALL达到最小值，此时的电阻、电抗即为所求解；判断UB_var-ALL是否达到最小值，主要有两方面的约束，第一：判断连续两次计算得到的UB_var-ALL是否均小于设定的终止约束公差，一般终止约束公差的设定值小于或等于0.0001，若对求解精度要求较高，终止约束公差的设定值一般小于或等于0.000001；第二：判断前后两次计算得到的均值UB_var-ALL的差值是否小于设定的差值阈值，一般差值阈值的设定值小于或等于0.00001，若对求解精度要求较高，差值阈值的设定值一般小于或等于0.000001；只有当这两个条件均满足时，才判定UB_var-ALL达到最小值，此时支路电阻、电抗即为所求解，终止迭代。如上所述，该问题转化为优化问题minUB_var-ALL(14)其约束条件为式(7)至(10)。有时，节点B是变压器的二次侧出口，这样节点B的电压就成为了可测量的量UB_measured。于是，优化问题的目标函数变为测量的UB_measured与每个电表计算 得到的UB的差值：min1NΣi=1n{1nΣj=1n[UB_measured(i)-UBj(i)]2}---(15)]]>其中，UB_measured(i)、UBj(i)分别表示时间间隔i时的节点B的电压测量值和利用第j个电表数据计算得到的电压值。下面再以另一种配电网为例，对本发明提供的技术方案做进一步详细说明：此种配网中，其拓扑如附图3所示。该拓扑包含17个智能电表和21条支路。电表的数据时间间隔为1小时，测量持续时间为1周，因此，每个电表的电压、有功功率和无功功率数量均为24×7＝168。节点A是变压器二次侧的出口，电压可测。为了分析利用节点A的测量电压和不利用节点A的测量电压计算结果的不同，该具体实施例分为以下2种情况：情况1.按照公式(14)的原理不利用节点A的测量电压计算配电网支路阻抗；情况2.按照公式(15)的原理利用节点A的测量电压计算配电网支路阻抗。情况1和情况2计算得到的电阻、电抗值如下表所示：表1两种情况下计算得到的配电网支路电阻、电抗目标函数的收敛情况如附图4所示。其中，实线表示情况1的收敛情况，虚线表示情况2的收敛情况，其收敛的条件均为终止约束公差为0.000001。附图4中实线趋于平缓的速度更快，表明情况1的收敛速度比情况2快；但是情况2的最终收敛值更接近最下方的水平坐标轴线，表明情况2的收敛误差更小，收敛误差越小收敛效果越好。附图5和附图6分别是利用情况1和情况2在目标函数值达到终止约束公差时得到的电阻、电抗值计算得到的UA误差曲线，曲线上的每一个点表示在第i个时刻利用第j个智能电表数据计算得到的UA和第i个时刻的目标UA(情况1中目标UA对应第i个时刻所有智能电表数据计算得到的UA平均值，情况2中目标UA对应第i个时刻UA的量测值)间的误差。利用情况1中电阻、电抗值计算得到的UA的误差如附图5所示。正最大误差出现在60小时处，其值为UA14的0.2439％；负最大误差出现在92小时处，其值为UA4的-0.2613％。同样，利用情况2中电阻、电抗值计算得到的UA的误差附图6所示。正最大误差出现在12小时处，其值为UA14的0.2009％；负最大误差出现在40小时处，其值为UA4的-0.2149％。由附图5-附图6中的结果分析知情况2的UA整体误差(以正最大误差、负最大误差以及平均误差为标准)更小，又因为配电网支路电阻、电抗值的准确度 以目标函数的收敛误差和UA的整体误差为标准，因此，基于图4中情况2的目标函数收敛误差更小以及图6中UA的整体误差更小，表明情况2下计算得到的电阻、电抗值更加准确。这并不难于理解。对于该方法的最优问题，上游节点即变压器二次侧出口处的电压值使得迭代始终围绕在真实的准确的测量值附近，这使得计算结果更加精确。以上仅为本发明的实施例而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均在申请待批的本发明的权利要求范围之内。当前第1页1 2 3