随机性检测方法和装置与流程
本发明涉及随机性检测技术,尤其涉及一种随机性检测方法和装置。
背景技术:
目前体育彩票、福利彩票等各类彩票在全国广泛发行,如何确保彩票发行的公正和公平,成为彩民最为关注,但又最难以解决的问题。
一般来说,彩票是通过摇奖机随机摇出规定数量的摇奖球,将摇奖球的标号作为中奖号码,因此,摇奖机的随机性关系到彩票发行是否公正和公平。然而,目前,仅是通过公证机构对摇奖机摇奖的过程加以公证,无法确保摇奖机的随机性,从而无法确保彩票发行的公正和公平。
技术实现要素:
本发明提供一种随机性检测方法和装置,使得通过对待检测中奖号码的随机性的检测从而确定出摇奖机的随机性,且对摇奖机的随机性进行了综合考量,从而确保摇奖机发行的公正和公平。
本发明第一方面提供的随机性检测方法,包括:
获取待检测中奖号码;
采用至少两种检验函数检测待检测中奖号码的随机性;
根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性。
本发明第二方面提供的随机性检测装置,包括:
提取单元,用于获取待检测中奖号码;
检测单元,用于采用至少两种检验函数检测待检测中奖号码的随机性;
确定单元,用于根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性。
本发明提供的随机性检测方法和装置,通过采用至少两种检验函数检测 待检测中奖号码的随机性,根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性,使得通过对待检测中奖号码的随机性的检测从而确定出摇奖机的随机性,同时,采用至少两种检验函数检测待检测摇奖机的随机性,对摇奖机的随机性进行了综合考量,从而确保摇奖机发行的公正和公平。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作一简单地介绍,显而易见地,下面描述中的附图是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动性的前提下,还可以根据这些附图获得其他的附图。
图1为本发明实施例提供的随机性检测方法流程图;
图2为本发明实施例提供的随机性检测装置结构示意图。
具体实施方式
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
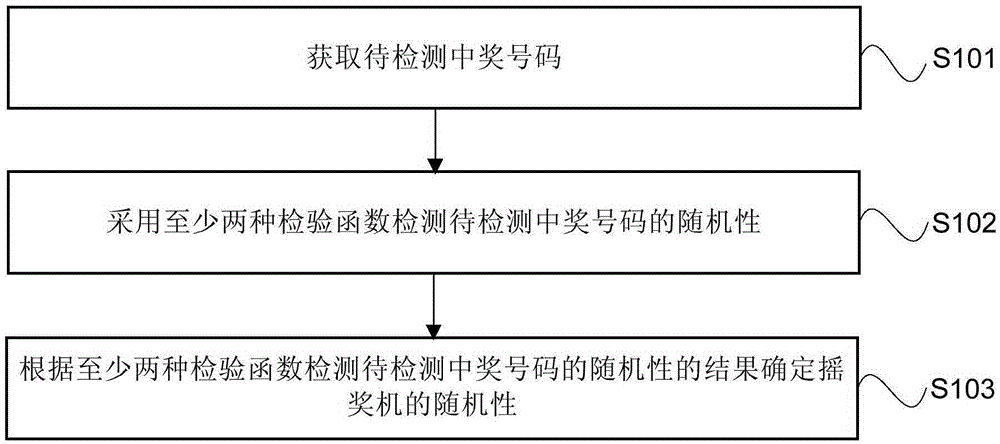
图1为本发明实施例提供的随机性检测方法流程图。如图1所示,本发明实施例提供的方法,包括:
S101:获取待检测中奖号码。
具体的,随机性检测装置在摇奖机正常工作状态下获取待检测中奖号码,获取的中奖号码不少于预设数值,比如获取的中奖号码不少于1000组。
需要说明的是,本发明实施例中的随机性检测装置可以是个人计算机(personal computer,简称PC机),比如笔记本和平板电脑等。
S102:采用至少两种检验函数检测待检测中奖号码的随机性。
具体的,本发明实施例中随机性检测装置通过采用至少两种检验函数对摇奖机出奖数据的随机性检测来判断出奖数据是否随机,进而反推出摇奖机 的随机性。
可选的,采用至少两种检验函数检测待检测中奖号码的随机性包括:
采用至少两种检验函数检测待检测中奖号码的整体随机性、序列连贯性、序列时域性和序列谱域性中至少一个性能。
其中,检验函数包括频数分布检验函数、最大RUN分布检验函数、最大ACF检验函数、HOC分布检验函数和非正态的独立同分布序列的谱函数中至少两个函数。
可选的,频数分布函数包括:Joe-1维频数分布检验函数、Joe-2维频数分布检验函数、极大值频数分布检验函数和极小值频数分布检验函数。
具体的,可以通过频数分布检验函数检验待检测中奖号码,反映中奖号码的整体随机性;通过最大RUN分布检验函数检验待检测中奖号码,反映中奖号码的序列连贯性;通过最大ACF检验函数或HOC分布检验函数检验待检测中奖号码,反映中奖号码的序列时域性;通过非正态的独立同分布序列的谱函数检验待检测中奖号码,反映中奖号码的序列谱域性。需要说明的是,本发明实施例并不仅限于此,也可以通过频数分布函数反映中奖号码的序列连贯性,通过最大RUN分布检验函数反映中奖号码的整体随机性等,本发明实施例不再赘述。
S103:根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性。
具体的,若待检测中奖号码通过任一种检验函数的检测,则待检测中奖号码具有随机性,摇奖机具有随机性;若待检测中奖号码通过所有检验函数的检测,则待检测中奖号码不但具有随机性,且具有较佳的随机性,摇奖机具有较佳的随机性。
可选的,根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性,包括:
若至少两种检验函数中任一种检验函数检测待检测中奖号码的接受概率大于等于预设接受概率,则确定待检测中奖号码是随机的,摇奖机具有随机性。
或者,若至少两种检验函数中任一种检验函数检测待检测中奖号码的拒绝概率小于等于预设拒绝概率,则确定待检测中奖号码是随机的,摇奖机具 有随机性。
可选的,预设接受概率为0.145。
或者,预设拒绝概率为0.30。
具体的,有的检验函数是通过接受概率检验待检测中奖号码是否具有随机性,比如频数分布检验函数;有的检验函数是通过拒绝概率检验待检测中奖号码是否具有随机性,比如非正态的独立同分布序列的谱函数。因此,检验函数通过判断待检测中奖号码是否大于等于接受概率或者小于等于拒绝概率检验待检测中奖号码是否具有随机性,若待检测中奖号码大于等于接受概率,或者待检测中奖小于等于拒绝概率,则确定待检测中奖号码是随机的,摇奖机具有随机性。
本发明实施例提供的随机性检测方法,通过采用至少两种检验函数检测待检测中奖号码的随机性,根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性,使得通过对待检测中奖号码的随机性的检测从而确定出摇奖机的随机性,同时,采用至少两种检验函数检测待检测摇奖机的随机性,对摇奖机的随机性进行了综合考量,从而确保摇奖机发行的公正和公平。
进一步地,在上述实施例中,关于Joe-1维频数分布检验函数和Joe-2维频数分布检验函数:
设从{1,2,…,N}中无放回地依次取出k个号码(x1,x2,…,xN),以下称之为一个k-维,所有这样的集合记为Yk(只看内容不计次序),则Yk共有个元素。假设k-维出现机会均等,令Xi={xi,1,xi,2,…,xi,k},i=1,2,…,n,n是k-维的独立n次抽样,则Xi是独立同分布(independent and identically distributed,简称i.i.d)的随机列,其中,在概率统计理论中,如果变量序列或者其他随机变量有相同的概率分布,并且互相独立,那么这些随机变量是独立同分布。设Oα为子集α在这n个k-维中出现的次数,如O{1}和O{1,2}分别表示{1}出现的次数和{1,2}出现的次数(只看内容不计次序),Oβ为子集β在这n个k-维中出现的次数,m(α)=j是α的维数,m(α,β)为α∩β交集中不同元素的个数,则统计量:
渐近服从自由度为的χ2分布,其中,Cj={(α,β):m(α,β)},
为了充分利用中奖号码先后顺序的信息,Joe还提出了二维有序检验的方法:
设Oα是α={i,j}出现的次数,其中,i<j,则统计量:
服从分布,其中,E=nk(k-1)/[2N(N-1)],α′={j,i}是α={i,j}的逆序,
S1={{α,β}:α,β中有一个共同元素且在相同的位置上},
S1={{α,β}:α,β中有一个共同元素但在不同的位置上},
b2=(6k2-6)N3+(-8k3-38k2+32k+26)N2,
b-2=(k-2)[(4k2-16)N2+(-3k3-19k2+29k+33)N+(12k3-2k2-28k-14)]C,
b1=-(k-2)[(6kN2+(-8k2-7k-5)N+(3k3+4k2-5k+4)]C,
b-1=(k-2)[6N2+(4k2-13k-11)N+(-3k3+4k2-5k+4)]C。
进一步地,在上述实施例中,关于极大值和极小值的分布检验函数:
假设中奖号码为{x1,x2,…,xk}=X,经排序后,记为:ξ1≤ξ2≤…≤ξk,即而{x1,x2,…,xk}序列是由{1,2,…,N}个号码均匀抽取的。可以得到,次序统计量ξk和ξ1分别遵从极大值和极小值的概率分布:
极大值概率分布:
极小值概率分布:
设为一串独立同分布的中奖号码,对于要检验ξk是否遵从极大值概率分布,ξ1是否服从极小值概率分布就变成了普通的对随机变量分布的检验问题。
进一步地,在上述实施例中,关于最大RUN分布检验函数:
本发明实施例中关于最大RUN分布检验函数主要集中在最长链的检验,设对给定的{xj,j=1,2,…,n}独立同分布于P(xj=1)=p,P(xj=0)=1-p,记其中最长的RUN为Ln,则对1≤k≤n,
进一步地,在上述实施例中,关于最大ACF检验函数:
给一个中奖号码序列的一段观测值最主要的是确定该观测值是否来自独立同分布的总体。本发明实施例在时域上对该观测值进行分析,设xt,t=1,2,…,T是零均值平稳序列的一组样本,
记s=0,1,2,…MT,其中,
则是xt相关系数的相合估计。
对H0:ρ(s)=δs,0及统计量
即当T充分大时,统计量渐近于N(0,1)分布,则在H0下,对若取为1-α,则可解得:
由正态密度积分可在给定之后查出χα临界值,如取=0.90,则
T=137时:m=10,x=0.2196;
T=160时:m=15,x=02132;
T=229时:m=20,x=0.1850。
进一步地,在上述实施例中,关于非正态的独立同分布序列的谱函数:
设xt,t=1,2,…,T是零均值平稳序列的一组样本,令0≤λ≤π,则的极限分布,等于
其中,γ=e+2,u4为4阶中心矩,Φ(x)是标准正态分布函数。
于是,在选择1-α水平下,其置信区间为:
或者对H0:xt是独立同分布序列的检验否定域为
举例来说,若1-α=0.90,θα=1.5205,T=137,σ2=107.917,则否定域为:
其中,
进一步地,在上述实施例中,关于HOC分布检验函数:
高阶交叉(High Order Crossing,简称HOC)分布检验函数是检验随机过程差分性质并可用于对白噪声检验的检验函数。设{Zt}是零均值的平稳列,令则称Dk,N为k阶的HOC,其中,为差分符号。
设Zt~N(0,σ2),则对充分大的N,有
其中,
由上可得正态白噪声条件下的区间估计,即在选择1-α水平下,对每个j,Dj,N应落入区间:
需要说明的是,对j=1,2,3,4,5,6,7,8,{Zt}只要有一个Dj,N落在区间之外,即可拒绝。
图2为本发明实施例提供的随机性检测装置结构示意图。如图2所示,本发明实施例提供的装置,包括:提取单元21、检测单元22和确定单元23。
提取单元21,用于获取待检测中奖号码。
检测单元22,用于采用至少两种检验函数检测待检测中奖号码的随机性。
确定单元23,用于根据至少两种检验函数检测待检测中奖号码的随机性的结果确定摇奖机的随机性。
本发明实施例的随机性检测装置用于执行图1所示方法实施例的技术方案,其实现原理和技术效果类似,此处不再赘述。
进一步地,在图2所示实施例中,检测单元22具体用于:
采用至少两种检验函数检测待检测中奖号码的整体随机性、序列连贯性、序列时域性和序列谱域性中至少一个性能;
其中,检验函数包括频数分布检验函数、最大RUN分布检验函数、最大ACF检验函数、HOC分布检验函数和非正态的独立同分布序列的谱函数中至少两个函数;
频数分布函数包括:Joe-1维频数分布检验函数、Joe-2维频数分布检验 函数、极大值频数分布检验函数和极小值频数分布检验函数。
进一步地,在图2所示实施例中,确定单元23具体用于:
若至少两种检验函数中任一种检验函数检测待检测中奖号码的接受概率大于等于预设接受概率,则确定待检测中奖号码是随机的,摇奖机具有随机性;
或者,若至少两种检验函数中任一种检验函数检测待检测中奖号码的拒绝概率小于等于预设拒绝概率,则确定待检测中奖号码是随机的,摇奖机具有随机性;
其中,预设接受概率为0.145;
或者,预设拒绝概率为0.30。
最后应说明的是:以上各实施例仅用以说明本发明的技术方案,而非对其限制;尽管参照前述各实施例对本发明进行了详细的说明,本领域的普通技术人员应当理解:其依然可以对前述各实施例所记载的技术方案进行修改,或者对其中部分或者全部技术特征进行等同替换;而这些修改或者替换,并不使对应技术方案的本质脱离本发明各实施例技术方案的范围。
- 还没有人留言评论。精彩留言会获得点赞!