计及VSG逆变器电流限幅的暂态能量函数方法与流程
本发明涉及一种电力系统暂态稳定分析以及非线性电力电子器件饱和特性研究技术,特别是一种计及vsg逆变器电流限幅的暂态能量函数方法。
背景技术:
随着风电规模的不断扩大,与电网相连的并网逆变器等电力电子变流器数量也得到快速的增加。由于电力电子器件采用数字电路的控制方式,暂态响应时间短,当电网中出现功率扰动或者功率不平衡情况时,无法和传统的同步发电机一样利用储存在转子上的动能来抑制功率或频率的波动。基于此,为了解决风电系统中因逆变器无惯性特性带来的稳定问题,国外研究人员首先提出了虚拟同步发电机技术(virtualsynchronousgenerator,vsg)。然而,系统总容量是一定的,风电渗透率的增加,使得传统同步发电机占有比例减少,系统惯性减小,从而对电力系统安全稳定运行造成很大威胁。当电网发生大扰动时,采用vsg策略的逆变器与传统同步发电机相似也会出现失稳问题,且由于逆变器存在电流饱和特性,此时逆变器会褪变成一个电流源,使得系统的暂态稳定问题更加复杂,因此针对vsg策略下计及逆变器电流限幅的风电系统暂态稳定分析方法研究,对于电网的安全稳定运行具有重要的实际应用价值。
目前,针对vsg策略下逆变器系统暂态稳定分析方法主要有数值仿真法和暂态能量函数法。数值仿真法通过对故障后vsg控制策略下的逆变器摇摆曲线的变化观察得到系统稳定性,但无法定量的对系统暂态稳定进行评价,由于模型比较精准复杂使得计算速度很慢,并且现有的数值仿真法在研究含vsg策略的逆变器系统暂态稳定性时并没有计及逆变器电流饱和特性的影响;暂态能量函数法克服了数值仿真法的计算速度慢和无法定量分析稳定性的局限性,在计及逆变器电流饱和特性的系统稳定性研究方面,现有的暂态能量函数法得出由于逆变器电流饱和的原因,在发生大的扰动下使得逆变器褪变成一个电流源,使失稳过程变得更加复杂,并作出了功角失稳的机理分析。但仅仅是定性地对vsg暂态功角失稳进行分析,对实际电网的安全稳定运行并没有根本性指导。
技术实现要素:
本发明的目的在于提供一种计及vsg逆变器电流限幅的暂态能量函数方法,包括以下步骤:
步骤1,构建逆变器的电流限幅模型;
步骤2,获取逆变器电流饱和下的功角特性;
步骤3,构建vsg策略下计及逆变器饱和的系统功角模型;
步骤4,构建改进后逆变器电流饱和环节模型,获取改进后的功角与未饱和时功角的关系;
步骤5,输入电气部分的主要参数,包括vsg、线路、变压器、故障位置和限幅装置电流的最大最小值;
步骤6,用龙格库塔法方法求解转子运动方程获取vsg转子的δ(t)与
步骤7,获取故障切除时刻系统暂态能量vcl与临界能量vcr;
步骤8,将步骤7求取的故障切除时刻系统暂态能量vcl与临界能量vcr比较,若vcl≤vcr,则系统稳定,否则系统失稳;
步骤9,求取临界故障切除时间。
本发明考虑到逆变器电流饱和特性会对风电系统暂态稳定性裕度产生不容忽视的影响,提出了采用反正切函数近似的改进方法,将电流饱和环节模型近似等效成反正切函数,构建了计及改进饱和环节的暂态能量函数,能够定量的对vsg策略下计及逆变器电流限幅的风电系统暂态稳定进行分析,本发明对逆变器电流饱和环节的改进能够使传统暂态能量函数方法对系统的暂态稳定性进行分析且满足要求,解决了传统暂态能量函数对含有逆变器电流饱和环节的系统稳定分析时系统能量存在的突变局限性。
下面结合说明书附图对本发明做进一步描述。
附图说明
图1是逆变器电流限幅环节示意图。
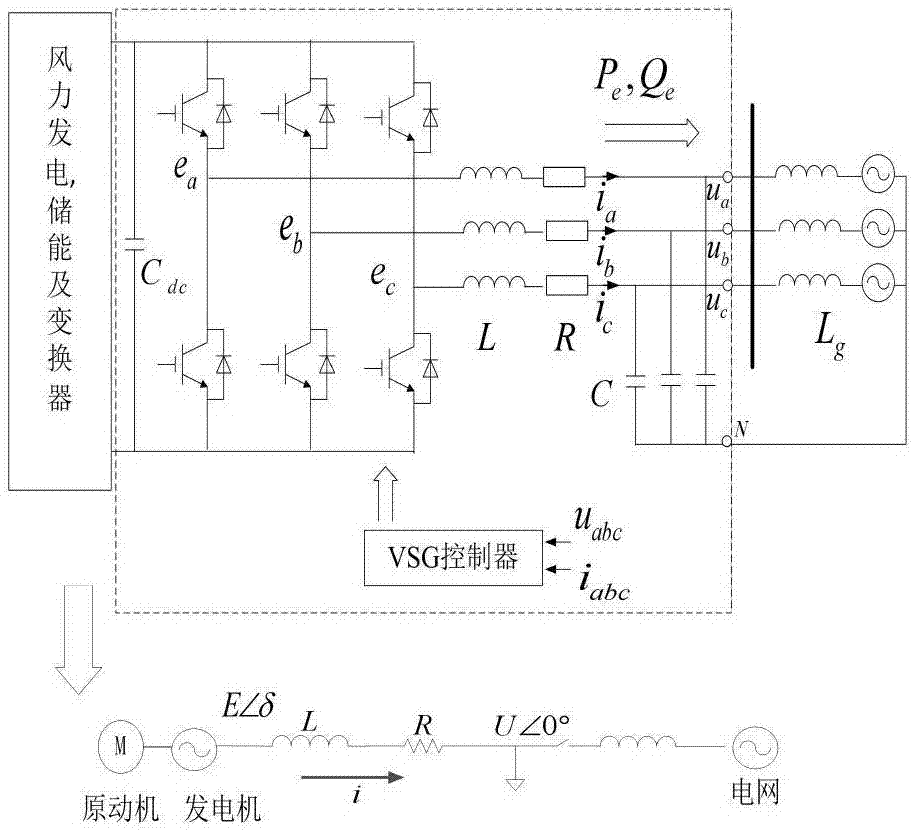
图2是单机无穷大系统示意图。
图3是电流限幅环节的改进示意图。
图4是系统稳定域示意图。
图5是故障切除后系统的动能、势能和总能量的变化关系示意图。
图6是本发明的方法流程图。
具体实施方式
本发明提出一种vsg策略下计及逆变器电流限幅的风电系统暂态能量函数法。当逆变器电流限幅时(实际的逆变器都有电流限幅,因为过流会损坏逆变器),传统的暂态能量函数方法不能判断vsg(虚拟同步发电机)系统暂态稳定性,本专利通过改进逆变器电流限幅环节模型,构建了计及改进电流限幅环节的暂态能量函数,并且能够正确判断vsg系统暂态稳定性。该方法考虑目前逆变器饱和环节的暂态能量函数分析存在的局限性,在此基础上,将电流饱和环节模型近似等效成反正切函数,借助于传统电力系统暂态稳定分析推导了逆变器电流饱和环节近似改进之后虚拟功角与传统电力系统功角之间的关系,并构建了计及改进饱和环节的暂态能量函数,能够定量的对vsg策略下计及逆变器电流限幅的风电系统暂态稳定进行分析。
能量轨线是指表示系统动能、系统位能以及系统总能量随时间变化的轨线,而故障轨线是指表示系统在故障期间角速度w随功角δ变化的轨线。
结合图6,计及改进饱和环节的暂态能量函数方法如下:
第一步,构建逆变器的电流限幅模型。
为了防止流经逆变器的电流过大对设备造成损害,逆变器运行中必须要设置电流限幅环节对其进行保护。选用dq轴电流动态限幅控制方式,令d轴电压外环的pi调节器输出电流为
其中,imax为逆变器限幅环节电流上限。
由式(1)和式(2)可得:当imag<imax时,逆变器电流限幅环节不起作用;当imag>imax时,逆变器电流限幅环节启动,电流被钳位在
第二步,构建考虑逆变器电流饱和的虚拟功角特性。
当电流达到最大值时,此时逆变器将变成一个电流源,其输出功率为:
式中:电网侧的功率因数角θ为
当电流饱和后,由于d轴电流优先的限幅方式的作用,d轴电流将逐渐增大到imax,q轴电流将逐渐减小到零。θ'=δ'+90°,
式中,δ'为d轴与
第三步,构建vsg策略下计及逆变器饱和的系统功角模型。
采用vsg控制策略的风力发电逆变器并网单元容量以兆瓦级计算,电网的其他部分可视作为无穷大系统,则单机无穷大系统如附图2所示。
对于图2所示的单机无穷大系统有以下关系成立:
式中,e为vsg机端电压;u为无穷大母线参考电压;x∑为线路电抗;i为逆变器输出电流;δ为vsg系统功角。
由式(6)可得电流幅值与功角之间关系如式(7)和(8)所示:
由式(8)可以看出,逆变器电流限幅转换为系统功角限幅,这样系统暂态稳定性减小。
第四步,构建改进后逆变器电流饱和环节模型
对逆变器电流饱和环节进行改进即将式(3)逆变器电流饱和数学模型近似成式(9)所示的反正切函数(如附图3所示),从而能够保证函数在任何一点处可导。逆变器电流饱和环节近似数学模型见图3,函数如式(9)所示:
根据式(8)和式(9),得到改进后的功角与未饱和时功角的关系:
式中:δ新为逆变器电流饱和环节近似改进之后的虚拟功角,δ原为未含饱和环节的传统电力系统功角。
第五步,采用等值单机无穷大系统进行仿真,系统参数标值:发电机电抗xd=0.3,变压器电抗xt=0.3,线路1的电抗xl1=0.5,线路2的电抗xl2=0.93,机端电压eb=0.90081,阻尼系数d=0.3,惯性时间常数h=0.35,发电机有功p=0.9,无功q=0.436。考虑逆变器电流限幅|i|<0.8,并根据式(8)转换为功角限幅。
得到未对饱和环节改进的系统能量函数:
以及对饱和环节改进后的系统能量函数:
仿真得到改进前后单机无穷大系统稳定域和能量变化曲线如图4和图5所示。
由图4(a)观察可知由于电流饱和,其稳定域虚拟功角被限制在最大值141.3°和最小值36.87°的区域范围内。图4(b)是对饱和模型进行改进后的系统稳定域,可知改进逆变器电流饱和环节之后,系统的稳定域边界相较于未改进的变大,这是因为改进时所采用的反正切函数是光滑连续的,因此系统的稳定域也不会出现限幅的情况。
由图5(a)观察可知,系统能量出现了突变,不能满足李雅普诺夫函数条件,即能量v的导数小于0,采用传统暂态能量函数分析vsg策略下计及逆变器电流限幅的系统稳定性是存在局限性的。
图5(b)是对饱和模型进行改进后的系统总能量变化曲线,是连续的没有出现突变问题,完全符合李雅普诺夫函数条件。根据上述仿真分析可知vsg策略下逆变器饱和环节改进之后,利用传统暂态能量函数能够对含逆变器电流饱和的系统暂态稳定性进行正确分析。
综上所述,采用上述技术方案后,本发明具有如下突优势:考虑到逆变器电流饱和特性会对风电系统暂态稳定性裕度产生不容忽视的影响,本发明提出了采用反正切函数近似的改进方法,将电流饱和环节模型近似等效成反正切函数,构建了计及改进饱和环节的暂态能量函数,能够定量的对vsg策略下计及逆变器电流限幅的风电系统暂态稳定进行分析,本发明对逆变器电流饱和环节的改进能够使传统暂态能量函数方法对系统的暂态稳定性进行分析且满足要求,解决了传统暂态能量函数对含有逆变器电流饱和环节的系统稳定分析时系统能量存在的突变局限性。
- 还没有人留言评论。精彩留言会获得点赞!