地下水对地铁盾构隧道施工影响的数值模拟分析方法与流程
本发明涉及一种数值模拟分析方法,尤其是一种地下水对地铁盾构隧道施工影响的数值模拟分析方法,属于地下水对地铁盾构隧道施工影响的分析领域。
背景技术:
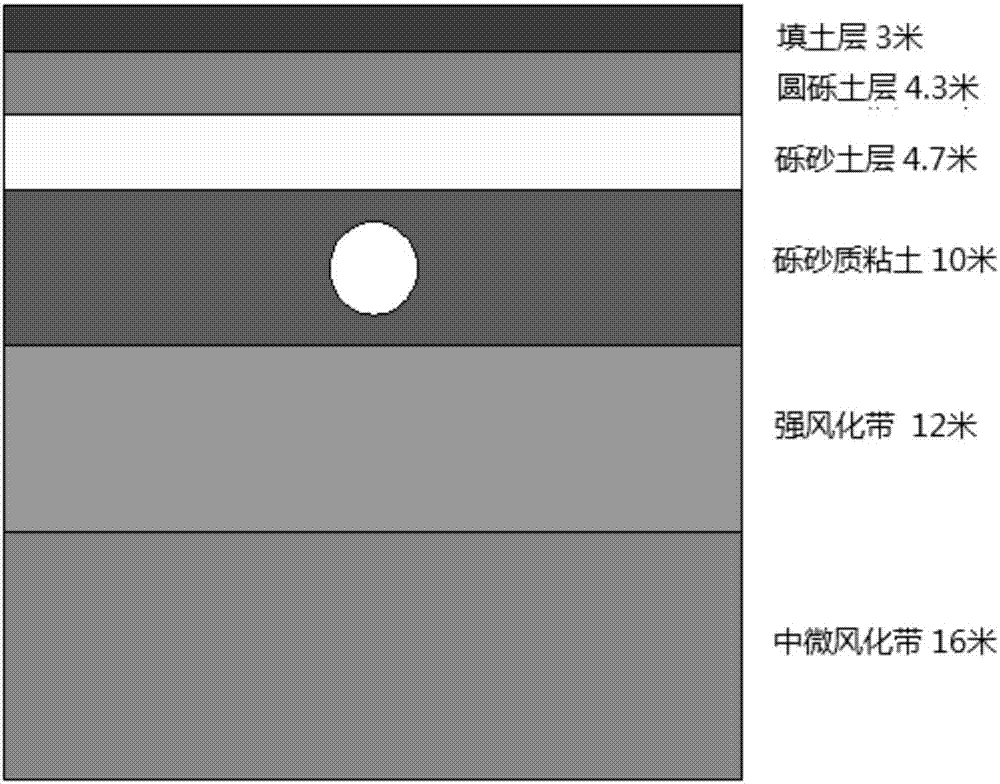
:进入21世纪以来,随着现代科学技术的发展和人口数量的增加,人类对赖以生存的空间的需求量不断增加。因此,对地下空间的合理开发和利用则成为城市未来重点发展的方向。与此同时,随着城市地铁施工技术的快速发展以及地下空间的进一步开发和利用,地铁成为缓解城市人口交通压力的重要交通工具。地铁隧道开挖的方法有很多种,其中常用的一种方法就是盾构法。隧道盾构法开挖是指大型盾构机在刚外壳的保护下,利用开挖面刀盘在设计隧道开挖线上对岩土进行挖掘,同时在盾构机后方形成衬砌结构支护已挖隧道,并通过顶推力装置不断向前安全推进的开挖方法。实际隧道盾构工程中,影响隧道和地层变形的因素繁多,而地下水作为岩土工程技术问题中急需突破和克服的难点之一,具有很大的研究发展空间。当隧道盾构施工在地下水贮藏丰富的土层或者富水砂层中进行时,盾构影响范围内的土体孔隙水压力和渗透系数均会随着隧道盾构的掘进而变化。同时,地层也会随着渗透系数的减小和孔隙水压力的消散而发生固结沉降,最终引起隧道和地层变形。目前,在实际地铁盾构隧道施工工程中,地下水对盾构隧道开挖的影响周期较长,但实测数据较少,使得与地下水相关的研究偏少。地下水作为影响隧道和地层变形的重要因素,隧道施工和运营过程中受地下水影响与限制的实例越来越多。因此,针对地铁盾构法施工中地下水影响效果的研究具有十分重要的工程意义。技术实现要素:本发明的目的是为了解决上述现有技术的缺陷,提供了一种地下水对地铁盾构隧道施工影响的数值模拟分析方法,该方法通过分析地下水对地铁隧道盾构施工的影响,以便对地铁盾构隧道施工段的工程进行保护,具有良好的应用前景。本发明的目的可以通过采取如下技术方案达到:地下水对地铁盾构隧道施工影响的数值模拟分析方法,所述方法包括以下步骤:s1、根据地铁盾构隧道施工段,对盾构隧道开挖进行数值模拟,建立初始模型;s2、在初始模型的基础上,通过对地下水所带来的附加应力进行数值模拟分析,建立不排水分析模型;s3、将初始模型和不排水分析模型计算得到的土体沉降数值进行对比,得到盾构隧道施工中地下水所带来的附加应力对土体沉降变形的影响情况;s4、在不排水分析模型的基础上,通过对地下水渗透作用和土体力学作用的耦合进行数值模拟分析,建立流-固耦合模型;s5、将流-固耦合模型、不排水模型和初始模型计算得到的土体沉降数值进行对比,得到盾构隧道施工中土体排水固结对土体沉降变形的影响情况;s6、通过改变流-固耦合模型的渗透系数和地下水位,建立不同的有限差分模型,得到不同渗透系数和地下水位下的地表沉降数值,进一步得到渗透系数和地下水位对地表沉降的影响情况。进一步的,步骤s1中,所述根据地铁盾构隧道施工段,对盾构隧道开挖进行数值模拟,建立初始模型,具体包括:s11、根据地铁盾构隧道施工段的工程地质、水文地质和周围环境,采用flac3d软件建立土体几何模型,该土体几何模型中,x方向为横截面方向,y方向为隧道纵向开挖方向,z方向为隧道埋深方向;s12、通过flac3d软件中的fix命令对土体几何模型进行初始边界条件的设置;s13、通过flac3d软件中的setgrav命令将土体自重赋值在土体几何模型的网格单元上,并设置模型的应力边界条件;s14、选取摩尔库伦模型作为土体几何模型的本构模型;s15、通过flac3d软件中的solve命令对土体几何模型进行初始应力平衡,即使土体几何模型的网格单元上的每个节点的应力位移均为零;s16、对盾构隧道开挖进行数值模拟,建立初始模型。3、根据权利要求2所述的地下水对地铁盾构隧道施工影响的数值模拟分析方法,其特征在于:步骤s16中,所述对盾构隧道开挖进行数值模拟,具体包括:a、采用flac3d软件中的shell命令进行超前支护模拟;b、采用flac3d软件中的null命令进行隧道开挖模拟盾构开挖面从y=0处开始,每步开挖2m;c、每步隧道开挖完成后,拆除上一步的超前支护,并在隧道内进行管片衬砌和注浆模拟;d、重复上述步骤a~c,直到盾构隧道开挖完成。进一步的,所述工程地质的材料参数包括凝聚力c、内摩擦角φ、泊松比v、体积模量k和剪切模量g;其中,所述体积模量k和剪切模量g通过下式进行转化:其中,e表示弹性模量,v表示泊松比。进一步的,步骤s4中,所述通过对地下水渗透作用和土体力学作用的耦合进行数值模拟分析,具体包括:s41、在flac3d软件中输入土层渗透系数以及孔隙水压力建立渗流场;s42、在flac3d软件中输入土层物理地质参数建立应力场;s43、在flac3d软件中,设置流固耦合分析的参数;s44、在flac3d软件中,设置渗流模式下的边界条件。进一步的,所述在flac3d软件中输入土层渗透系数以及孔隙水压力建立渗流场,具体如下:根据饱和土的连续性,单位时间内土体微元总压缩量等于x、y、z方向的单元表面流量变化之和,如下:其中,代入上式后,得到:其中,kx、ky、kz分别表示土体微元x、y、z方向上的渗透系数;qx、qy、qz分别表示单位时间内微元表面x、y、z方向上的流量;u表示孔隙水压力,εv表示土体微元的体积应变,t表示渗流时间。进一步的,所述在flac3d软件中输入土层物理地质参数建立应力场,具体如下:根据土体有效应力原理,表示研究平面上的总应力σ、有效应力σ‘与孔隙水压力u之间的关系,如下:σ=σ‘+u其中,σ表示土体微元总应力,σ‘表示土体微元有效应力。根据土体微元的平衡可以推导出土体静力平衡方程为:其中,γ表示土体重度,τxy、τxz、τyz表示土体微元的剪切应力,σx、σy、σz分别表示土体微元x、y、z方向上的应力;在考虑有效应力σ‘情况下,将上式改写为:其中,σ’x、σ'y、σ'z分别表示土体微元x、y、z方向上的有效应力;土体微元骨架为线弹性体且满足广义虎克定律,则土体本构方程为:其中,εv表示土体微元的体积应变,g表示剪切模量,v表示泊松比,εx、εy、εz分别表示土体微元x、y、z方向上的有效正应变,γx、γy、γz分别表示土体微元x、y、z方向上的有效切应变;假设土体微元处于小变形状态,得到几何方程为:其中,wx、wy、wz分别表示土体微元在x、y、z方向上的位移;根据土体的平衡方程、本构方程、几何方程三式,得到由位移wx、wy、wz和土体孔隙压力u表示的平衡方程:进一步的,所述流固耦合分析的参数包括渗透参数、密度、流体模量、孔隙率、饱和度和流体抗拉强度;其中,所述密度包括土体干密度、土体饱和密度和流体密度,所述流体模量包括比奥模量和流体体积模量。进一步的,所述渗透参数与土力学渗透参数的换算关系如下:k(m2/pa/sec)=k(cm/s)×1.02×10-6在渗流模式中,需要设置土体干密度,土体饱和密度通过下式自动计算:ρs=ρd+nsρf其中,n表示孔隙率,s表示饱和度,ρd表示土体干密度,ρs表示土体饱和密度;在无渗流模式下,对于位于地下水位以下的土体,需要设置饱和密度;所述比奥模量按下式计算:其中,kf表示流体体积模量,α表示比奥系数,k表示介质的体积模量,m表示比奥模量;所述流体体积模量按下式计算:其中,kf表示介质的流体体积模量,δp表示流体压力增量,δvf表示流体体积增量,vf表示流体体积。进一步的,所述渗流模式下的边界条件包括不透水边界条件、透水边界条件和其他渗流条件。本发明相对于现有技术具有如下的有益效果:本发明方法利用有限元差分软件flac3d建立三维模型,对隧道盾构施工中地下水的影响效果进行了系统的分析,对隧道开挖中盾尾径向注浆压力的施加、水泥浆层的硬化、地应力的逐步释放等细节进行了详细的模拟,也对地下水渗流作用与土体力学作用的耦合关系进行了合理的设置,进一步分析了渗透系数与地下水位等地质参数在隧道施工中,对地表沉降变形的影响,具有创新意义,拥有广泛的工程应用前景。附图说明图1为本发明实施例的数值模拟分析方法流程图。图2为本发明实施例的隧道底层结构示意图。图3为本发明实施例的土体几何模型示意图。图4a为本发明实施例的盾构开挖示意图。图4b为本发明实施例的超前支护示意图。图4c为本发明实施例的衬砌管片示意图。图5为本发明实施例的盾构隧道开挖剖面示意图。图6a为本发明实施例的初始模型土体的横向位移云图。图6b为本发明实施例的初始模型土体的纵向位移云图。图7a为本发明实施例的初始模型在隧道拱顶位置y=25m处的沉降曲线图。图7b为本发明实施例的初始模型在隧道拱底位置y=25m处的沉降曲线图。图8为本发明实施例的初始模型在地表y=25m处的纵向沉降变形图9为本发明实施例的初始模型在地表y=25m、y=35m、y=45m处横向沉降曲线图。图10a为本发明实施例的不排水分析模型的土体横向沉降云图图10b为本发明实施例的不排水分析模型的土体纵向沉降云图。图11为本发明实施例的不排水分析模型在y=25m、y=35m、y=45m位置横向地表沉降。图12为本发明实施例的不排水分析模型与初始模型在地表y=25m处纵向地表沉降对比图。图13为本发明实施例的不排水分析模型与初始模型在地表y=25m处隧道拱顶纵向沉降对比图。图14为本发明实施例的不排水分析模型、peck修正公式和初始模型得到的y=45m处横向地表沉降对比图。图15a为本发明实施例的流-固耦合模型横剖面竖向沉降分布云图。图15b为本发明实施例的流-固耦合模型纵剖面竖向沉降分布云图。图16为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在隧道拱顶位置y=25m处沉降对比图。图17为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在隧道拱底位置y=25m处隆起对比图。图18为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在地表y=25m处纵向地表沉降对比图。图19a为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在地表y=25m处横向地表沉降对比图。图19b为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在地表y=35m处横向地表沉降对比图。图19c为本发明实施例的流-固耦合模型与不排水分析模型、初始模型在地表y=45m处横向地表沉降对比图。图20为本发明实施例不同渗透系数所记录的地表y=25米处横向地表沉降变形对比图。图21为本发明实施例不同渗透系数所记录的地表y=25米处纵向地表沉降变形对比图。图22为本发明实施例不同地下水位所记录的地表y=25米处横向地表沉降变形对比图。图23为本发明实施例不同地下水位所记录的地表y=25米处纵向地表沉降变形对比图。具体实施方式实施例:本实施例选取广州地铁三号线北延段某一地铁区间的盾构隧道施工段,借助有限差分软件flac3d进行模拟。如图1所示,本实施例的地下水对地铁盾构隧道施工影响的数值模拟分析方法,包括以下步骤:1)根据地铁盾构隧道施工段,对盾构隧道开挖进行数值模拟,建立初始模型本实施例采用flac(fastlagrangiananalysisofcontinua)3d建立模型,flac3d是一款研究三维连续介质受到内外部各种影响下,达到平衡或者稳定塑流状态下的机制行为的显示差分软件,flac3d软件采用命令驱动的形式,通过向软件输入命令的方法,实现对模型的控制与修改,从而得到预想的数值模型。flac3d数值模拟主要分为四步骤:建立有限差分网格、赋值材料参数、定义初始条件和边界条件以及求解。其中,模型的几何形状可以通过网格来划分;模型力学特性可以通过材料参数赋值来反映;而模型的初始状态可以通过边界条件和初始条件来定义。本实施例将从盾构隧道施工段的工程地质、水文地质、周围环境三方面进行分析。1.1)工程地质本实施例选取的地铁区间场地由第四系和白垩系下统白鹤洞组组成,第四系上部由全新统冲洪积层的圆砾、卵石和粘性土组成;第四系中部由上更新统冲洪积层形成的砾砂质黏土、粘性土和砾砂组成;第四系下部由中更新统残积层形成的砾(砂)质黏土组成;白垩系下统白鹤洞组由红褐色泥质粉砂岩、粉砂质泥岩、砂砾岩和细砂岩组成。根据以上土层地质分布,可得土层物理参数统计表如下表1所示:表1土层物理参数表由于使用flac3d有限差分软件进行模拟,在对材料进行赋值时都是通过体积模量k和剪切模量g来进行赋值的。因此,建模过程输入的材料参数为体积模量k和剪切模量g,而不是弹性模量e以及泊松比v;其中,k和g之间存在着如下变换关系:本实施例的模型土层一共分为六层,由上到下分别为:填土层、砾砂土层、砾砂质黏土、强风化带、中微风化带。隧道埋深位于地表以下17m;圆形隧道的内外径分别为5.4m和6.0m;衬砌管片宽度和厚度分别为2m和250mm。由此可得隧道地层结构如图2所示。1.2)水文地质本实施例选取的地铁区间场地内地下水主要由松散土层孔隙水和基层风化裂隙水两部分组成,孔隙水主要赋存于第四系冲洪积砾砂层中,而基层风化裂隙水主要赋存于强风化带-中等风化带的基岩裂隙中。1.2.1)河水水文本区间主要穿越城市道路以及居民区,地下水贮存较为丰富。1.2.2)土层的富水性以及渗透系数分析本区间地层从垂直剖面观看,自上而下可以分为填土、圆砾土、砾砂细砂、砾砂质粘土、强风化花岗岩、中微风化花岗岩等六层。根据每层土体的物理化学性质,现对每层土体的富水性和渗透性进行分析,分析结果如下:a、填土层多数为杂填土,而杂填土内主要由建筑垃圾和卵石组成。因此,本土层的渗透性为中等,属于中透水层。b、圆砾土层内主要由卵石和砾石两部分组成,土层渗透性较好,属于中强透水层。c、砾砂土层内主要由砾石和中砂组成,同时土层内含有少部分细砂,渗透性好,属于中强透水层。d、砾砂质粘土层内由于部分砾砂的存在,土层渗透性较好,属于中等偏强透水层。e、全风化花岗岩的渗透性中等,属于中透水层。f、强风化花岗岩的渗透性较弱,属于中等偏弱透水层。g、中微风化花岗岩的渗透性弱,属于弱透水层。1.3)周围环境本实施例选取的地铁区间全程一共贯穿47栋主要建筑。同时,根据实地调研分析:47栋建筑物中包括住宅楼、厂房和商业楼。其中,住宅楼以3-7层的民宅为主,且最高层数为9层(共4栋),而厂房和商业楼则占据了主要部分。这些建筑物都有一些共同特点:大部分建筑为框架结构,房屋年久失修。因此,隧道盾构施工中应加强对地表沉降控制的要求。同时,根据调查结果表明:本区段内主要地下线路有排水、供水以及供电等地下管线。由于该区段远离工业区,整个路线范围内并没有发现煤气和相关工业管道。1.4)土体几何模型的建立根据所选工程背景的地质条件可知,整个土体地层可以分为6层。现利用flac3d进行相应几何模型的建立。在充分考虑隧道盾构开挖对周围土体的扰动影响以及模型计算速度的情况下,现初拟定几何模型的尺寸为。其中,x方向为几何模型横截面方向;y方向为几何模型的隧道纵向开挖方向;z方向为隧道埋深方向。根据设计的单元网格大小(单元网格划分为1米),整个几何模型一共有48500个网格和50075个网格节点,如图3所示。1.5)初始边界条件的设置土体几何模型所涉及到的边界条件有两种:应力边界条件和位移边界条件。其中,应力边界条件可以由初始地应力的计算确定。而位移边界条件的设定需要充分考虑模型的计算速率和是否符合工程实际两大因素。因此,现将模型两侧边界设定为简支边界,模型底部边界为固支边界。而模型边界条件的设定可以通过flac3d中fix命令进行操作。1.6)初始应力的模拟根据选取的工程地质条件,初始应力的计算需要考虑两种因素:土体自重和地下水。由于初始模型中不考虑地下水对模拟的影响,在计算初始应力时可以忽略孔隙水压力的影响,只需要对土体重力进行赋值。而在flac3d中可以通过setgrav命令将土体自重赋值在模型网格单元上。应力边界条件的设置(与初始应力有关)对模型的计算有着非常重要的影响。如果没有设置应力边界条件,模型在土体重力作用下就会发生位移,这种位移直到模型内应力与初始应力达到平衡后位移才会停止,这种情况使得模型的计算效率变得低下。所以,利用flac3d进行初始应力的模拟时,不仅需要设置土体重力,还应该设置模型的应力边界条件。模型初始应力包括两个水平方向应力σx,σy和一个竖直方向应力σz;其中,水平应力σx和σy在数值上相等,σx、σy和σz的计算公式如下:σz=σ0+∑γihi(3)σx=σy=k0σz(4)其中,σ0表示地表应力(mpa),γi表示第i土层重度(kn/m3),hi表示第i土层厚度(m),k0表示土层静止土压力系数。根据选取的工程地质条件,模型土层自上而下分别为:填土、圆砾、砾砂、砾砂质粘土、强风化带和中微风化带。这六种土层的土体重度一般在18-25kn/m3之间。考虑到模型的计算速度和工程实际情况,现将模型的土体重度统一取为22kn/m3;同时,地表应力取为零。根据几何模型可知,隧道中心轴线为三维坐标系中的y轴(即隧道埋深中心位置为坐标零点)。此时,隧道中心零点处竖向初始应力σz为:σz=σ0+∑γihi=-17×22=-374kn/m2(5)其中,负号表示应力为压应力。将土层的静止土压力系数k0取为0.5,那么隧道中心零点处水平初始应力σx,σy分别为:σx=k0σz=0.5×(-374)=-187kn/m2(6)σy=k0σz=0.5×(-374)=-187kn/m2(7)土压力梯度公式grad可以按照下式进行计算:其中,σ1表示模型底部竖向应力(mpa),h表示模型z方向上的厚度(m)。由式(3)可得模型底部z方向竖向应力σ1为:σ1=σ0+γh=-50×22=-1100kn/m2(9)由式(9)得模型z方向的竖向应力σz的应力梯度为:1.7)土体本构模型的确定flac3d软件中内置了许多材料的本构关系,以适应不同材料或者研究方向下的模拟要求。结合本实施例选取的工程地质条件,土层处于沿海软土地区,大部分土体处于弹塑性形态,结合各类本构模型的优势和局限性,最终选取摩尔库伦(mohr-coulomb)模型作为本实施例模型的本构模型。1.8)初始应力的平衡进行初始模型的盾构开挖模拟前,需要对模型进行初始应力平衡,即使模型单元网格上的每个节点的应力位移均为零,可以通过flac3d中solve命令进行操作。在综合考虑模型计算时间和平衡收敛的情况下,现将初始模型到达平衡的歩时设定为5000,即模型计算到5000步时达到平衡收敛。1.9)盾构开挖初始模型在模拟隧道盾构开挖过程时考虑了三方面因素:超前支护、注浆层和管片衬砌。由于盾尾空隙的存在,其与衬砌之间的空隙会导致上覆土体损失而引起沉降,这也是模拟中需要考虑的方面。盾尾空隙一般是由三部分组成:一是盾构机外壳所占体积;二是为了方便衬砌拼装而提前预留的操作空间;三是盾构机刀盘超开挖间隙。在隧道盾构开挖模拟中,如何处理衬砌管片与围岩之间的注浆体是模拟的关键。目前,模拟中经常使用的处理注浆体的方法有:a、认为注浆体完全填充盾尾空隙。b、不考虑注浆作用,认为围岩直接与衬砌相互作用。c、不考虑注浆作用,认为围岩的人缩径量就是盾尾空隙。d、认为注浆体的厚度等于盾尾空隙的折减。为了方便模拟,本实施例对注浆体的处理采用第一种方法:即认为注浆体可以完全填充满盾尾空隙。同时,在影响围岩稳定性的各项因素中,除去可以通过试验测定的土体以及衬砌的力学性质外,盾尾空隙、土体向盾尾空隙的自然填充程度、注浆的分布情况和隧道壁面受扰动程度等方面都无法通过常规的试验进行测定。此时,就需要提出等代层的概念。等代层囊括了以上各个方面,它的力学参数和物理参数在不同的地层和施工工艺环境中可以有不同取值。为了方便模拟,本实施例的模型模拟过程中将等代层视为一个均匀的环形。同时,管片衬砌、注浆液和支护装置的材料参数如下表2所示:模拟材料厚度/m体积模量k/mpa剪切模量g/mpa密度kg/m2衬砌0.2522e313.5e32500注浆液0.052221672100支护装置0.11.5e70.9e72500表2盾构支护材料参数表盾构开挖步骤如下:a、隧道盾构开挖是逐步进行的,在进行下一步盾构开挖前,需要采用flac3d软件中的shell命令进行超前支护模拟;盾构开挖如图4a所示,超前支护如图4b所示b、采用flac3d软件中的null命令进行隧道开挖模拟盾构开挖面从y=0处开始,每步开挖2m;初始模型的隧道长度为50米,故开挖步一共25步,使用软件中的null命令进行隧道开挖模拟;c、每步隧道开挖完成后,拆除上一步的超前支护,并在隧道内进行管片衬砌和注浆模拟;衬砌管片的示意图如图4c所示,d、重复上述步骤a~c,直到盾构隧道开挖完成,即建立初始模型;盾构隧道开挖剖面如图5所示。1.10)初始模型的沉降结果分析本实施例的盾构开挖完成后,可以获得土体的横向位移云图和纵向位移云图分别如图6a和图6b所示。隧道拱顶沉降由隧道拱顶位置逐渐向土体上方蔓延,而隧道拱底位置的隆起则逐渐向下方土体扩散。本实施例的隧道开挖过程中,模型记录了隧道拱顶位置y=25m处和隧道拱底位置y=25m处的沉降曲线分别如图7a和图7b所示。从图中分析可知,隧道拱顶沉降分为三个阶段:缓慢变形阶段、急剧变形阶段和变形稳定阶段。当开挖掌子面没有开挖到y=25m处时,拱顶位置没有发生较大沉降,大约为1.01mm,此时沉降处于缓慢变形阶段;而当掌子面通过该截面处时,拱顶位置在短距离内发生了较大位移,此时沉降处于急剧变化阶段;随着隧道开挖深度的增加,拱顶沉降逐渐处于变形稳定阶段,最终取值为16.42mm。隧道拱底处于缓慢变形阶段时的隆起量约为0.44mm,隧道拱底处于急剧变形阶段时的最大隆起可达12.90mm,隧道拱底隆起处于稳定阶段时的最终隆起值为13.81mm。盾构开挖不仅对隧道有着重要影响,对地表沉降同样有着不可忽视的影响。模型记录了隧道开挖过程中地表y=25m处的纵向沉降变形,如图8所示,从图中分析可知,地表沉降随着隧道开挖深度增加而逐渐增加,最终沉降趋于稳定。其中,盾构通过该记录点y=25m处时,地表沉降在短距离内有较大增加。当隧道全部开挖完毕之后,该记录点最终沉降值为7.30mm。对于横向地表沉降而言,模型记录了地表y=25m、y=35m、y=45m处横向沉降曲线,如图9所示,从图中分析可知,隧道开挖后,沉降最大值发生在隧道中心轴线地表处,随着地表距离隧道中心轴线距离增大,沉降逐渐减小,整个沉降曲线图呈“漏斗形”凹槽。此时,y=25m处横向地表沉降最大值为7.30mm;y=35m处横向地表沉降最大值为7.72mm;y=45m处横向地表沉降最大值为9.09mm。2)在初始模型的基础上,通过对地下水所带来的附加应力进行数值模拟分析,建立不排水分析模型在考虑地下水过程中,隧道盾构开挖一般可以分为两种分析方法:不排水分析以及排水固结分析,排水固结分析即所谓的流固耦合分析。flac3d对于地下水的分析一般采用渗流模式,在渗流模式中,也可以进行不排水计算。此时只需要直接设置土体的不排水体积模量,同时在计算的时候关闭流体场。不排水分析与流固耦合分析的本质区别在于:不排水分析认为初始孔隙水压力分布场不会随着盾构开挖而改变;而在流固耦合分析中,孔隙水压力随着隧道开挖深度而不断改变。同时,不排水分析将地下水视为静水,仅考虑其存在所带来的附加应力,并不考虑地下水的流动渗透性;而流固耦合分析则需要考虑地下水的渗透性和土体力学性质的耦合。3)将初始模型和不排水分析模型计算得到的土体沉降数值进行对比,得到盾构隧道施工中地下水所带来的附加应力对土体沉降变形的影响情况本实施例针对隧道开挖中不排水分析进行模拟,并与初始模型进行对比。根据不排水分析模型,可得到土体横、纵向沉降云图分别如图10a和图10b所示,从图中可知,相比于初始模型,不排水分析模型加入了地下水因素后的总体沉降量增大了;其中,不排水分析模型记录了y=25m、y=35m、y=45m位置横向地表沉降,如图11所示,从图中可知,y=25m处横向地表最大沉降为11.87mm,y=35m处横向地表最大沉降为10.80mm,y=45m处横向地表最大沉降为11.01mm,相比初始模型显著提高。同时,不排水模型记录了地表y=25m处纵向地表沉降和地表y=25m处的隧道拱顶纵向沉降,并与初始模型进行对比,分别如图12和图13所示,从图中可知,不排水分析模型中,y=25m处纵向地表沉降最大值为11.87mm,而初始模型y=25m处纵向地表沉降最大值为7.30mm,同比增长了62.66%。不排水分析模型整体纵向沉降相比初始模型的纵向沉降显著增大。同时,相比于初始模型,不排水分析模型隧道拱顶位置最大沉降量为27.46mm,同样有着显著增加。现有的预测地表沉降方法有四种:经验公式法、理论解析法、数值分析法和试验模拟法。每一种方法都有各自的优缺点,并不能完全适应各种地质情况。而岩土工程问题素来复杂,涉及的因素非常多。因此,目前并没有哪一种方法能够较为准确地预测不同地质情况下的地表沉降值。但是,相比于其他预测方法,经验公式法作为一种由实践积累推导出来的方法,是目前较为通用预测地表沉降的方法。为了突显地下水对隧道盾构的影响,现将不排水分析模型、peck修正公式和初始模型得到的y=45m处横向地表沉降数值进行对比,如图14所示,从图中可知,描绘出来的曲线形状基本吻合,但沉降数值有较大差别,不排水分析模型所得出的横向地表最大沉降比初始模型中的横向地表最大沉降稍大,而不排水模型和初始模型计算所获得的横向地表最大沉降量均比利用peck修正公式计算获得的横向最大沉降量小,初始模型最大沉降数值小59%左右;而不排水模型最大沉降数值小22%左右。究其原因,造成误差原因有三个:a、peck修正公式属于经验公式,本来就存在一定误差,比如,地层损失率的取值就具有一定的误差性。b、在建模过程中,模型一些参数输入存在一定的问题,尤其是地下水和各类土层并非均匀分布,而为了方便建模,假设地下水水位和各类土层均匀分布。c、建模过程中,并未考虑地面建筑荷载对地表沉降的影响4)在不排水分析模型的基础上,通过对地下水渗透作用和土体力学作用的耦合进行数值模拟分析,建立流-固耦合模型本实施例针对地下水渗流和土体力学的相互作用进行研究,通过有限差分软件flac3d对地铁盾构隧道中的非降水施工进行流固耦合数值模拟分析,建立相应的流-固耦合模型。同时结合广州地铁三号线北延段某一地铁区间的盾构隧道施工段的实际工程,对盾构隧道开挖中土体排水固结过程进行数值分析。4.1)地下水和土体的相互力学作用flac3d采用快速拉格朗日方法模拟岩土的流固耦合机理,将岩土体视作多孔介质,流体在孔隙介质中的流动满足达西定律,土体也需要满足几个相关方程,下面针对流固耦合分析的几个基本方程进行介绍。4.1.1)静水压力多孔介质中,任意一点的静水压力p为:p=γw·h(11)其中,γw表示水的重度(n/m3),h表示计算点的水头高度(m)。4.1.2)渗流力土体中的地下水具有流动性,而正是由于地下水的流动性引起了水头的损失。而这种水头损失是地下水在土体孔隙流动过程中,试图拖拽土体而消耗了能量的结果。与此同时,水流在拖拽土体的过程中同样会对土体施加一种拖拽力,也就是我们所谓的渗流力,亦可以称为渗透力、动水压力,设单位面积土体内土粒给予水流的阻力为:fs=γwi(12)其中,i表示水力梯度(m),fs表示单位面积内土体对水流的阻力(n);根据力的平衡定律,渗流力的大小等于单位面积内土体给予水流阻力的大小,且方向相反。因此,渗流力j为:j=fs=γwi(13)由于渗流力的存在,土体内部受力情况,包括大小和方向都会发生改变,而这种变化通常来说对于土体的稳定性有着不利的影响。但是,如果渗流力方向和土体重力的方向一致,那么此时渗流力反而会促使土体变得密实,有利于增强土体的强度和稳定性。相反的,如果渗流力的方向和土体重力的方向相反,那么渗流力的存在对土体的强度和稳定性均是不利的,特别是当渗流力大于土体的有效重度时,土粒将会被水冲出,形成流土,这对土体的稳定性是非常不利的4.1.3)岩体变形对地下水的影响岩体内的孔隙、裂隙和溶洞在控制地下水流向的同时,也给地下水的补给、径流和排泄提供条件。随着人类活动的不断增加,地铁隧道工程不断兴建,这些活动都不同程度上导致了岩土体变形,尤其是隧道盾构施工。隧道盾构施工改变了岩土体的结构,致使岩土体的地应力发生改变。而岩土体的变形同样也影响着地下水的活动4.2)渗流-应力耦合分析使用flac3d进行渗流-应力耦合分析时,在求解孔隙水压力的差分方程中引入应力的变形结果,将不同时步交替分配给程序做渗流分析和应力分析,从而体现出渗流场和应力场的耦合关系。在求解渗流场各个点的孔隙水压力后,再根据有效应力原理计算渗流场各个单元的有效应力。4.2.1)渗流场控制方程根据饱和土的连续性,单位时间内土体微元总压缩量等于x、y、z方向的单元表面流量变化之和,如下:其中,代入式(14)后,得到:其中,kx、kv、kz分别表示土体微元x、y、z方向上的渗透系数(m/d);qx、qv、qz分别表示单位时间内微元表面x、y、z方向上的流量(m3/m2·d);u表示孔隙水压力(mpa),εv表示土体微元的体积应变,t表示渗流时间(s)。4.2.2)应力场控制方程4.2.2.1)土体有效应力原理根据土体有效应力原理,表示研究平面上的总应力σ、有效应力σ‘与孔隙水压力u之间的关系,如下:σ=σ‘+u(16)其中,σ表示土体微元总应力(mpa),σ‘表示土体微元有效应力(mpa)。4.2.2.2)土体平衡方程根据土体微元的平衡可以推导出土体静力平衡方程为:其中,γ表示土体重度(n/m3),τxy、τxz、τyz表示土体微元的剪切应力(mpa),σx、σy、σz分别表示土体微元x、y、z方向上的应力;在考虑有效应力σ‘情况下,将上式改写为:其中,σ’x、σ'y、σ'z分别表示土体微元x、y、z方向上的有效应力(mpa);4.2.2.3)土体本构方程土体微元骨架为线弹性体且满足广义虎克定律,则土体本构方程为:其中,εv表示土体微元的体积应变,g表示剪切模量,v表示泊松比,εx、εy、εz分别表示土体微元x、y、z方向上的有效正应变,γx、γy、γz分别表示土体微元x、y、z方向上的有效切应变;假设土体微元处于小变形状态,得到几何方程为:其中,wx、wy、wz分别表示土体微元在x、y、z方向上的位移(m);根据土体的平衡方程、本构方程、几何方程三式,得到由位移wx、wy、wz和土体孔隙压力u表示的平衡方程:4.3)流-固耦合数值模拟分析4.3.1)流-固耦合模型参数设置4.3.1.1)渗透系数渗透系数是进行流-固耦合分析的重要参数之一。值得关注的是,flac3d中渗透系数k采用国际单位(m2/pa/sec),而我们常见的土力学渗透系数的单位则采用(cm/s)或(m/d)。两者之间并不是一一对等关系,而是存在着换算关系。土力学中渗透系数k与flac3d中渗透系数的单位换算关系如下:k(m2/pa/sec)=k(cm/s)×1.02×10-6(23)由上式可知,通过查阅文献、经验取值或者试验得到土层的渗透系数后,需要根据公式(23)将渗透系数换算成国际单位,然后在用于flac3d计算。通常来说,实际工程的土层分布情况较为复杂,可能含有两个甚至多个土层,而且每个土层的渗透系数都有差异。因此,利用flac3d模拟得到的土体模型就存在着两个或两个以上的渗透系数。这些渗透系数在数值上的差异大小不一,而决定模型时间步长短的则是最大渗透系数。稳态渗透计算中,人为减小模型中各个渗透系数间的差异,可以有效地提高渗透计算的收敛速度。目前,常见的各类土体的渗流系数如下表3所示。表3土体渗透系数表4.3.1.2)密度flac3d模拟过程中,常见的密度参数有三种:土体干密度ρd、土体饱和密度ρs和流体密度ρf。渗流模式中,只需要设置土体干密度,flac3d会按照下式自动计算土体饱和密度。ρs=ρd+nsρf(24)其中,n表示孔隙率,s表示饱和度;在无渗流模式下,对于位于地下水位以下的土体,需要设置饱和密度。4.3.1.3)流体模量flac3d渗流模式中涉及到一个非常复杂的参数:流体模量。流体模型一般包括比奥模量和体积模量。在流固耦合计算中,流体模量的选取对渗流计算时间有着非常大的影响,且在不同情况下有着不同的取值。因此,本小节将对流体模量进行详细介绍。a、比奥系数和比奥模量比奥系数可定义为单元体中土体体积模量与流体体积模量的差值与该单元土体体积模量的比值。flac3d模拟过程中,除了按照上述定义计算得到比奥系数外,比奥系数还可以通过土体排水试验测得的排水体积模量来确定。比奥系数的取值范围在到1之间,其中,n是土体的孔隙率。理想多孔介质中,比奥系数α与体积模量k和土体体积模量ks存在的关系如下式:其中,k表示介质的体积模量(mpa),ks表示介质的土体体积模量(mpa),α表示比奥系数。比奥模量m可定义为单元体中不排水体积模量ku与土体体积模量k的差值与比奥系数α的平方的比值。比奥模量m可按如下公式计算:其中,ku表示介质的不排水体积模量(mpa),m表示比奥模量(mpa)理想多孔介质中,比奥模量m与流体体积模量kf的关系为:假设土体呈不可压缩的情况下,flac3d默认比奥系数α的值取为1,即α=1。此时,比奥模量m为:b、体积模量流体体积模量是描绘流体可压缩性程度的物理量。流体体积模量可定义为流体压力增量与流体压力作用下引起的流体体积应变的比值:其中,kf表示介质的流体体积模量(mpa),δp表示流体压力增量(n),δvf表示流体体积增量(m3),vf表示流体体积(m3);利用flac3d进行模拟时,可将常温下纯水的体积模量取为2×109pa。c、流体模量和计算收敛速度的关系渗流模式中,流体模量对流体计算的收敛速度有着重要的影响。由于流体模量在不同节点的位置不同,故流体对于计算收敛速度存在不同的影响。a、对于饱和渗流分析来说,流体模量(比奥模量或者体积模量)的取值不会影响计算的收敛速度。这是因为达到稳态所需的流动时间及流体计算的时间步都与流体模量(m或者kf)成反比。因此,不管设置多大的模量,所需要的迭代数都是相同的,所需要的时间也是相同的。b、对于有浸润面的稳态渗流分析中,使用较低的体积模量可以有效的加快问题的收敛,因为饱和度增量计算公式中涉及到时间步。c、对于完全流固耦合问题的分析非常复杂,一般来说,如果流体模量(m或者kf)越大,则问题收敛速度越慢。从数值分析的角度来说,流体模量的数值不必大于20倍或者4.3.1.4)孔隙率flac3d中将孔隙率的取值默认为0.5,一般来说,孔隙率取值范围在0到1之间。但是,因为流体模量的取值与孔隙率相关(kf/n),如果孔隙率取值过小(比如小于0.2)时,那么流体模量会远远大于土体材料的模量了。这种情况下会导致计算收敛速度变得很慢。当遇到孔隙率过小时,可以适当的减小流体模量中体积模量(kf)的取值;4.3.1.5)饱和度和流体抗拉强度flac3d中饱和度一般设置为1,而流体的抗拉强度则默认为取值为-1015。4.3.2)渗流模式下的边界条件4.3.2.1)不透水边界条件flac3d程序中,模型边界默认为不透水边界。如果不进行边界条件的设定,那么程序默认为边界上的节点与外界没有任何的流体交换,节点上的孔隙水压力值可以自由变化。4.3.2.2)透水边界条件在模型的边界节点上,设置孔隙水压力固定则表示该边界为透水边界。流体可以沿着该透水边界自由地流入或者流出模型边界。4.3.2.3)其他渗流条件根据赋值对象的不同,flac3d程序的渗流边界条件可以分为节点渗流条件。单元渗流条件和平面渗流条件。上述设置完成后,即建立流-固耦合模型。5)将流-固耦合模型、不排水模型和初始模型计算得到的土体沉降数值进行对比,得到盾构隧道施工中土体排水固结对土体沉降变形的影响情况本实施例模拟的土体采用摩尔-库伦模型,假定管片衬砌以及注浆材料均为弹性模型。同时,认为地表和土层呈均匀水平层状分布。计算中不考虑因为管片搭接或者错缝拼接质量所带来的影响。隧道盾构开挖过程中,盾构机每次推进步长为2m,在每个推进步完成后,立即设置管片衬砌和注浆。地下水位在模型中近似取为地表,模型左右两边的边界条件均为透水边界条件,模型底部为不透水边界。5.1)盾构开挖对隧道的影响本实施例的模型主要分析渗流条件下隧道盾构施工中土体排水固结对土体沉降变形的影响。根据建立的流-固耦合模型,获得模型横、纵剖面竖向沉降分布云图、横、纵向地表沉降曲线和隧道拱顶拱底变形曲线。其中,模型横、纵剖面竖向沉降分布云图分别如图15a和图15b所示,从图中可知,土体的沉降由隧道拱顶位置开始向地表逐渐减小;隧道拱底发生隆起现象,越往下,隆起越小;在图15b中,模型开挖后边界沉降相比于其它位置较大,越靠近边界,沉降越大,究其原因,模型可能出现这种结果有三个原因:1)盾构快速开挖引起的较大沉降;2)模型边界效应;3)前两种原因的共同作用;考虑了地下水的渗透作用,模拟了地下水作用下土体发生排水固结,从而导致了地层发生沉降变形。本实施例的流-固耦合模型记录了隧道拱顶底位置y=25m处和隧道拱底位置y=25m处的沉降变形,并和初始模型、不排水分析模型中的隧道拱顶、拱底沉降作对比,所得结果分别图16和图17所示,从图中可知,耦合模型隧道拱顶位置y=25米处最大沉降量约为37.10mm,隧道拱底隆起最大值约为14.60mm;不排水分析模型拱顶位置y=25米处最大沉降量约为27.46mm,隧道拱底隆起最大值约为12.91mm而初始模型隧道拱顶位置y=25米处最大沉降量约为16.42mm,隧道拱底隆起最大值约为13.81mm。耦合模型拱顶沉降最大值相较于不排水分析模型大了35.1%;而相较于初始模型,耦合模型拱顶沉降最大值更是大了125%,整整一倍有余。因此,在考虑地下水渗透作用下,土体排水固结对隧道拱顶所带来的影响非常明显。同时,相较于初始模型和不排水分析模型,耦合模型中隧道拱底隆起值增加幅度较小,只有微小增加。5.2)盾构开挖对地表沉降的影响本实施例的流-固耦合模型也记录了隧道开挖过程中地表y=25m处的沉降变形,同时和初始模型、不排水分析模型中地表y=25m处的沉降变形作对比,如图18所示,从图中可知,隧道盾构开挖完成后,流-固耦合模型中,地表y=25m处最大位移沉降约为22.11mm,不排水分析模型地表y=25m处最大位移沉降约为11.87mm,而初始模型中地表y=25m处最大位移沉降约为7.30mm。相较于初始模型以及不排水分析模型的地表纵向最大沉降值,流-固耦合模型地表最大沉降值分别大了14.81mm和10.24mm,接近一倍差值。因此,在富含地下水的地层中,排水固结所带来的地表沉降是土体沉降的主要部分,对地表沉降有着非常显著地影响;本实施例的流-固耦合模型也记录了地表y=25m,y=35m、y=45m处横向地表沉降曲线,分别如图19a、图19b和图19c所示,从图中可知,耦合模型中y=25m、y=35m、y=45m处横向地表最大沉降值分别为22.11mm、20.88mm以及22.08mm。由图可知,在相同位置处,相比于不排水模型以及初始模型的最大沉降值,耦合模型的最大沉降值有着非常大的变化。由此分析可知,富水地层中,土体排水固结对地表沉降所带来的影响是完全不能忽视的重要方面。6)通过改变流-固耦合模型的渗透系数和地下水位,建立不同的有限差分模型,得到不同渗透系数和地下水位下的地表沉降数值,进一步得到渗透系数和地下水位对地表沉降的影响情况6.1)土体排水固结后渗透系数的计算隧道盾构开挖过程会引起地下水渗流现象,导致地层中的孔隙比逐渐减小。而渗透系数随着不断减小,渗透系数与孔隙比之间存在着一定的关系。可以由下式表示:其中,k、k0分别为孔隙率n、n0所对应的渗透系数。土的压缩性主要体现在土体的竖向变形和横向变形,其中,土体的竖向变形占据着主要作用。根据土体的侧限压缩试验和相关理论,土体固结变形后的孔隙率和土层变形量与变形前的孔隙率和土层厚度之间的关系可以由下式表示:根据上两公式,可以得到土体固结沉降后土体渗透系数:6.2)不同渗透系数下的土体沉降以本实施例的隧道工程为例,模拟当渗透系数为:0.049m/d、0.49m/d、4.9m/d的情况下,隧道盾构开挖对地表沉降的影响,建立三个有限差分模型。其中,本实施例的实际工程中隧道盾构所在土层的渗透系数为4.9m/d。6.2.1)土体横截面地表沉降、纵向地表沉降在不同渗透系数下,模型均记录地表y=25米处横向地表沉降变形,根据获得的数据可绘制如下地表横向沉降对比图,如图20所示。时,模型也记录了地表y=25米位置处的地表纵向沉降变形,根据获得数据可得如下纵向沉降对比图,如图21所示。从图20和图21中分析可知,地表沉降,不管是横向沉降还是纵向沉降,都随着渗透系数的增加而增加。其中,渗透系数为0.049m/d,地表y=25米处最大沉降约为16.41mm;渗透系数为0.49m/d,地表y=25米处最大沉降约为19.11mm;渗透系数为4.9m/d,地表y=25米处最大沉降约为22.11mm。6.3)渗透系数变化对实际工程的影响本实施例模拟的流-固耦合模型中,对于土体的渗透系数采用常数假设处理,即在模拟过程不考虑渗透系数变化对耦合过程的影响。一般来说,随着土体排水固结过程不断发展,渗透系数也随着发生改变,对土体沉降有一定的影响。为了验证本次流-固耦合模型的合理性,模拟过程中对各土层的变形进行了监测,同时运用上述土体固结后渗透系数公式进行分析,选取隧道开挖区域以及以上区域进行计算,计算结果如下表4所示。表4渗透系数变化百分比6.4)地下水位变化对实际工程的影响盾构隧道的埋深通常位于地表10m以下的位置,绝大多数的隧道都处于地下水位线以下,并长年受到地下水位升降的影响。当地下水位发生变化时,如果盾构隧道深埋其中,也会随着必然受到地下水位升降的影响,影响主要体现在隧道的变形以及地表沉降。本实施例主要针对地下水位位于地表0m、地表以下2m以及地表以下4m三种情况进行地表沉降的分析,建立三个有限差分模型。6.4.1)土体横截面地表沉降、纵向地表沉降在不同地下水位下,模型均记录地表y=25米处横向地表沉降变形,根据获得的数据可绘制如下地表横向沉降对比图,如图22所示。同时,模型也记录地表y=25米位置处的地表纵向沉降变形,根据获得数据可得如下纵向沉降对比图,如图23所示。从图22和图23中分析可知,随着地下水位的降低,地表沉降,不管是横向沉降还是纵向沉降,都随着地下水位的降低而增加。当地下水位位于地表0m时,y=25m处的地表最大沉降值为22.11mm;当地下水位位于地表-2m时,y=25m处的地表最大沉降值为24.80mm;当地下水位位于地表-4m时,y=25m处的地表最大沉降值为28.30mm。由此可知,地下水对于地表沉降有着重要的影响。因此,本发明通过分析地下水对地铁隧道盾构施工的影响,以便对地铁盾构隧道施工段的工程进行保护,具有良好的应用前景。以上所述,仅为本发明专利较佳的实施例,但本发明专利的保护范围并不局限于此,任何熟悉本
技术领域:
的技术人员在本发明专利所公开的范围内,根据本发明专利的技术方案及其发明构思加以等同替换或改变,都属于本发明专利的保护范围。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1