一种随机孔隙岩体抗压强度与孔隙率的函数关系模型的利记博彩app
本发明属于地质和岩土工程技术领域,可应用于水利水电、基础设计建设等工程领域,尤其涉及一种随机孔隙岩体抗压强度与孔隙率的函数关系模型。
背景技术:
天然状态下的岩石,其内部分布着大量的微裂隙,由于这些微裂隙的存在,使岩石材料在力学性质上表现出明显的不连续性和各向异性。岩石的破坏往往都是由于在外部应力的作用下,其内部微裂隙的萌生、扩展和贯通所导致的。早期,传统的岩石强度理论是基于经典连续介质力学,把岩石看成等效的连续介插,结合试验归纳的方法得到的经验型强度准则。如1900年提出的mohr-coulomb强度准则,1952年提出的drucker-prager准则以及1980年提出的hoek-brown准则等,这些强度准则奠定了岩石力学理论发展的基础。
然而,由于岩石是一种内部孕育着大量的微孔洞、微裂隙等缺陷的复杂固体介质材料,在断裂机理研究方面,英国物理学家griffith早在1921年就提出了裂纹在脆性材料内部萌生和扩展的概念,建立了众所周知的griffith准则。在岩石损伤机理方面,20世纪70年代损伤力学和细观力学的建立和形成,将岩石强度理论的研究推进了一个新的发展阶段,并提出了许多适用的岩石损伤模型。
目前,对含缺陷岩石力学特性的研究包括在单轴、双轴和三轴压缩条件下的加载试验,所用的研究对象多为相似模型材料(如石膏、水泥、砂浆等)。由于水泥、石膏、砂子等材料加工浇筑成含某种裂隙缺陷的类岩石试件制取相对容易,因此相似模型试验被国内外的许多学者采用,并取得了大量的研究成果。
采用含预制规则裂隙的类岩石材料研充裂隙对岩石力学特性的影响规律,虽然能够在一定程度上研究其基本的影响特征和机制,但显然存在较大的局限性和不足,而针对含天然微裂隙和孔隙等缺陷的岩石力学性能及缺陷扩展、演化机制的研究少有报道。为此,一些学者开始在试验材料上做出了一些改进,通过“人工定制”的方法对预制裂隙的真实岩石进行试验研究,这样可更加真实地研巧天然状态下含裂隙岩石的力学特性。这种通过对真实岩石试件进行加工,经人为设置的预制孔洞或裂隙与天然发育而成的裂隙之间依然存在很大的区别,对岩石力学特性的影响也有所不同,试验结果难免会与含天然裂隙和孔隙的岩石试件存在一定的差异。
对天然完整岩石的物理力学试验研究较多,主要是对试验数据进行数理统计。不同文献中,试验数据中的强度与孔隙率存在一定的线性统计关系、对数统计关系或指数统计关系。得到的统计关系式中,数学表达式仅代表该组数据,不能说明各统计关系中系数代表的物理力学意义,不能复制或扩展,并未得到统一的强度与孔隙率之间的模型关系。对含天然随机缺陷的岩石的数理统计和规律性总结研究鲜有所见。
技术实现要素:
本发明的目的是提供一种随机孔隙岩体抗压强度与孔隙率的函数关系模型,通过强度与孔隙率之间的关系模型,将岩体的力学强度与物理性质联系起来,以克服现有技术的不足。
本发明基于以下技术思路:
岩石是自然界中由一种或多种矿物质组成的复杂地质体,由于成岩作用和成岩环境的差异,其内部通常含有大量从微观的隐裂隙到宏观的节理、孔洞等随机分布的缺陷。比如,贵州寒武系白云岩灰岩地层普遍发育隐裂隙(娄山关群等),三叠系关岭组灰岩、白云岩地层中发育数层晶洞灰岩(马马崖一级水电站),四川遂宁组红层泥岩中多见晶孔。这些节理、孔隙的存在破坏了岩石的连续性和完整性,使岩石在构造上显现出不连续性和各向异性等特点,在很大程度上改变了岩石的力学性质,从而导致其在力学性质上表现出较大的离散性和随机性。近年来,随着我国经济的高速发展,基础建设如火如荼,许多大型水利水电工程、交通运输设施和矿山等工程正在进行大规模的建设。对于存在的原始缺陷(如孔洞、裂隙等)岩石或岩体,需要研究其物理力学性质,提供合适的物理力学参数。
岩石的抗压强度是其基本的强度参数之一,是研究岩石力学性质的基础。对含随机的裂隙和孔隙缺陷的岩石来说,宏观的孔隙率直接代表了随机的裂隙和孔隙缺陷的发育程度。孔隙率不易直接测量,但是比重和密度是容易直接测得的,孔隙率通过比重和密度换算。天然完整岩石的强度与孔隙率存在一定的关系,现有文献有一定的研究,主要是对试验数据进行数理统计,不同文献中,试验数据中的强度与孔隙率存在一定的线性统计关系、对数统计关系或指数统计关系。得到的统计关系式中,数学表达式仅代表该组数据,不能说明各统计关系中系数代表的物理力学意义,不能复制或扩展,并未得到统一的强度与孔隙率之间的模型关系。
本发明是这样解决以上问题的:
本发明在大量实验数据的基础上提出一种随机缺陷岩石抗压强度与孔隙率之间的函数关系模型,该函数关系模型为幂函数关系模型,其中,指数为常数-1/2,其系数代表了孔隙率为1%时的完整岩石抗压强度。
该幂函数关系模型考虑了岩石抗压强度与孔隙率之间存在式(1)的关系:
式中:
rc为缺陷岩体抗压强度,单位mpa;
r1为孔隙率为1%时的完整岩石抗压强度,单位mpa;
n为缺陷岩石孔隙率,单位%;
岩石的孔隙率通过比重和干密度换算,根据式(2)计算得到:
式中:
gs为岩石的比重;
ρd为岩石的密度,单位g/cm3;
n为缺陷岩石孔隙率(开口孔隙率和封闭孔隙率),单位%;
根据式(2)带入式(1)中得到:
r1通过孔隙率在1%左右的完整岩石常规的抗压强度试验统计得到,如果完整岩石均不包含1%的孔隙率,则通过绘制完整岩石的rc-n曲线,外延得到。
对标准尺寸的含均匀随机孔隙岩石,通过实验测定岩石的比重和密度,通过式(3)计算其单轴抗压强度。
对地质体,可以实验室取样测定其比重,现场测定其密度,通过式(3)计算其岩体的强度。为后续的其他计算和工程设计提供强度参数。
本发明根据长时间积累的带随机孔隙天然岩石试件的大量物理力学试验数据,进行了回归统计,发现均匀随机缺陷岩石强度与孔隙率之间存在较好的幂函数关系,指数为常数-1/2,其系数代表了孔隙率为1%时的抗压强度,从而建立了具有物理力学意义的强度与孔隙率的模型关系,建立了强度与孔隙率的模型基本方程式,具有可复制性和推广性,可应用于岩石破损机理研究。岩石的孔隙率难以直接测量,但是孔隙率可以通过比重和干密度换算,岩石的比重和干密度是容易准确测量的。
发明给出了标准尺寸的含均匀随机缺陷岩石的强度衰减规律,通过实验测定岩石的比重和密度,通过本发明可以计算其单轴抗压强度。
对地质体,可以实验室取样测定其比重,现场测定其密度,通过本发明计算其岩体的强度。为后续的其他计算和工程设计提供强度参数。
附图说明
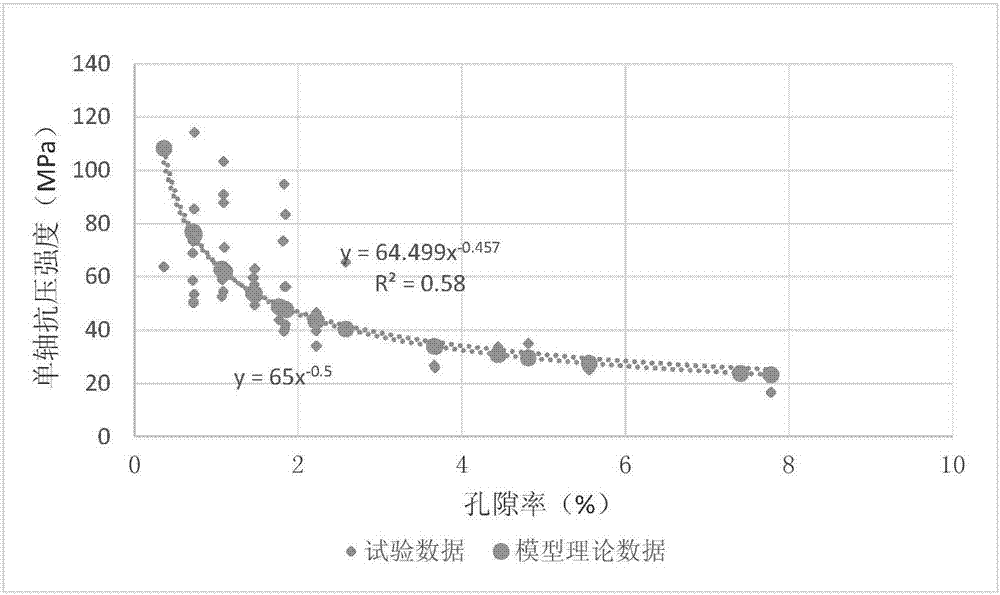
图1是某晶洞灰岩饱和抗压强度试验数据与模型理论数据对比关系;
图2是某晶洞灰岩天然抗压强度试验数据与模型理论数据对比关系;
图3是某裂隙白云岩天然抗压强度试验数据与模型理论数据对比关系;
图4为本发明岩石抗压强度与孔隙率之间的关系模型曲线。
具体实施方式
下面结合附图和实施例对本发明作进一步说明,但不作为对本发明的任何限制。
如图4所示,本发明的函数关系模型为幂函数关系模型,其中,指数为常数-1/2,其系数代表了孔隙率为1%时的抗压强度。
该幂函数关系模型考虑了岩石抗压强度与孔隙率之间存在式(1)的关系:
式中:
rc为缺陷岩体抗压强度,单位mpa;
r1为孔隙率为1%时的完整岩石抗压强度,单位mpa;
n为缺陷岩石孔隙率,单位%;
岩石的孔隙率通过比重和干密度换算,根据式(2)计算得到:
式中:
gs为岩石的比重;
ρd为岩石的密度,单位g/cm3;
n为缺陷岩石孔隙率(开口孔隙率和封闭孔隙率),单位%;
根据式(2)带入式(1)中得到:
r1通过孔隙率在1%左右的完整岩石常规的抗压强度试验统计得到,如果完整岩石均不包含1%的孔隙率,则通过绘制完整岩石的rc-n曲线,外延得到。
式(3)可以解释不同尺寸规模的岩石或地质体的尺寸效应,对尺寸规模越大的岩体,其孔隙率一般会增大,相应的强度也会有规律的降低。
对标准尺寸的含均匀随机孔隙岩石,通过实验测定岩石的比重和密度,通过式(3)计算其单轴抗压强度。
对地质体,可以实验室取样测定其比重,现场测定其密度,通过式(3)计算其岩体的强度。为后续的其他计算和工程设计提供强度参数。
本发明的技术方案的几个实例可参与图1-图3进行理解,其中图1是某晶洞灰岩饱和抗压强度试验数据与模型理论数据对比关系,图2是某晶洞灰岩天然抗压强度试验数据与模型理论数据对比关系,图3是某裂隙白云岩天然抗压强度试验数据与模型理论数据对比关系。
当然,以上只是本发明的具体应用范例,本发明还有其他的实施方式,凡采用等同替换或等效变换形成的技术方案,均落在本发明所要求的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!