一种基于半阈值追踪算法的荧光分子断层成像重建方法与流程
本发明属于分子影像技术领域,尤其涉及一种基于半阈值追踪算法的荧光分子断层成像重建方法。
背景技术:
荧光分子断层成像(简称fmt)是近年发展起来的一种具有在体研究前景的新型成像模态。它利用外部近红外光光源激发荧光探针(荧光团、荧光染料等),使荧光探针发射光子,利用荧光采集装置(一般为ccd相机)收集荧光信号,结合光传输模型的数学建模,可以获得重建目标内荧光探针的位置和浓度,实现对活体状态下的生物过程进行细胞和分子水平的定性和定量研究。目前被广泛用于疾病早期诊断、疗效监测、新药研发等领域。荧光分子断层成像的数学模型属于逆问题,具有严重病态性。根本原因在于光的强散射特性,使得光子在生物体内部的传输不再沿直线传播,而是经过大量无规则的散射过程。同时,实验采集的荧光数据局限于成像目标表面,而且采样点数量有限,使得逆问题是典型的欠定方程求解问题,进一步增加了求解问题的不适定性。多点激发和有限角度投影能够增加测量数据,一定程度上缓解问题的不适定性。但由此也带来了新的问题,测量数据中的冗余数据增多,计算时耗增加。为了精确定位目标位置,必须从大量的冗余数据中重建出少量有效解;于是,选择数学模型,如何用更合适的算法求解模型,得到更精确的解是荧光分子断层成像研究的核心问题。
综上所述,现有技术存在的问题是:目前采集荧光的测量数据中的冗余数据增多,计算时耗增加。
技术实现要素:
针对现有技术存在的问题,本发明提供了一种基于半阈值追踪算法的荧光分子断层成像重建方法。
本发明是这样实现的,一种基于半阈值追踪算法的荧光分子断层成像重建方法,所述基于半阈值追踪算法的荧光分子断层成像重建方法采用多点激发,有限角度测量,构建非凸问题稀疏正则模型,建立表面的测量数据与荧光目标分布的线性关系,将线性关系转化为1/2范数极小化问题求解,获得重建目标内部的荧光目标的三维分布与浓度;通过阈值迭代和匹配追踪算法对模型求解;
所述1/2范数极小化问题表示为:
其中,λ是正则化参数,a是系统矩阵,x是要求解的荧光目标三维分布与浓度,光通量密度φm。
进一步,所述基于半阈值追踪算法的荧光分子断层成像重建方法包括以下步骤:
步骤一,获取荧光测量数据;
步骤二,获得重建对象的解剖结构信息以及光学特性参数;
步骤三,利用amira软件对成像目标进行离散获得网格结构相关信息;
步骤四,基于光传输模型和有限元理论,将重建目标的解剖结构信息和光学特性参数作为先验信息,建立表面有限角度的荧光数据与重建目标内部荧光目标分布的线性关系;
步骤五,将线性关系转化为1/2范数极小化问题:
λ是正则化参数;
步骤六,对模型,采用半阈值迭代技术求解,引入半阈值算子如下:
于是,半阈值迭代技术用表示为如下形式:
其中,b(x)=x+at(φ-ax);
步骤七,为了减少步骤六中的迭代次数,引入追踪方法,令b(x)≈x,于是每次迭代有如下过程:
步骤八,通过步骤七中的迭代过程,得到第n步的重建结果xn。当||φ-axn||/||φ||≤1e-05或者||xn-xn-1||≤1e-08时,停止迭代;
步骤九,利用amira软件对成像目标进行离散获得网格尺寸较细的网格;
步骤十,显示结果,将重建结果和成像目标的解剖结构进行图像融合,用tecplot软件进行显示。
进一步,所述步骤一具体包括:
1)激发光源对固定在电控旋转台上的重建目标进行有限角度的透射式断层成像;透射式断层成像,将激光器与光学检测仪器放置在成像目标的两侧,激光照射重建目标激发荧光目标发出荧光,荧光穿透成像目标被激光器对面的光学检测仪器检测到;有限角度透射式断层扫描,用电脑控制电控旋转台等间隔旋转一大于90°;
2)使用光学检测仪器获得测量数据,获得光通量密度φm。
进一步,所述步骤二具体包括:
a)重建对象的解剖结构信息
对计算机断层成像投影数据进行三维重建,并用3dmed软件预处理获得成像目标的三维体数据;采用3dmed软件中的人机交互式半自动化分割方法对体数据进行组织分割,获得成像目标的解剖结构;
b)获取光学特性参数
利用解剖结构信息和应用基于生物组织特异性的光学三维重建方法的基于区域的扩散光学层析成像算法获得成像目标内各个组织的光学特性参数。
进一步,所述步骤四具体包括:
(1)光传输模型,采用扩散近似方程来描述光在成像目标内的传输过程;
(2)根据有限元理论,并融合重建目标的解剖结构信息和光学特性参数,将扩散近似方程离散,构建表面的测量数据与重建目标内部荧光目标分布的线性关系:
φm=ax;
其中a是系统矩阵,x是要求解的荧光目标三维分布与浓度,是非负的。
本发明的另一目的在于提供一种应用所述基于半阈值追踪算法的荧光分子断层成像重建方法的荧光分子断层成像系统。
本发明的优点及积极效果为:采用多点激发,有限角度测量。建立表面的测量数据与荧光目标分布的线性关系,将线性关系转化为1/2范数极小化问题求解,获得重建目标内部的荧光目标的三维分布与浓度;1/2范数对问题的解进行了进一步的稀疏化约束,充分的利用了问题的目标的稀疏特性,能够得到更为精确的重建结果。1/2范数最小化问题同时也是一个非凸性问题,存在着重建时间长,结果不稳定等缺陷。为了提高重建质量,我们采用半阈值追踪算法;通过半阈值算法求解目标问题,在阈值迭代过程中选择候选支持集时加入追踪的思想,减少迭代次数;通过结合阈值算法对参数稳定性和追踪算法逐步最优选择的优点,能够实现高质量重建的同时,增加参数稳定性和减少重建时间。
本发明基于光传输理论与有限元方法,利用了光学特性参数和解剖结构等先验信息,采用多点激发,有限角度测量,构建非凸问题稀疏正则模型,通过阈值迭代和追踪算法对模型求解;结合阈值迭代的算法的对参数的稳定性和追踪算法逐步最优的特点,有效提高了荧光分子断层成像的重建结果,增加了算法对于参数的稳定性,加快了非凸问题的求解过程,在光学断层三维重建算法等领域有重要的应用价值。
本发明采用的多点激发,有限角度测量,增加了测量数据,有利于减少问题的病态性;利用光学特性参数与解剖结构信息作为先验知识,提高了重建结果的准确性与重建图像的质量;将重建问题转化为有约束条件的1/2-范数极小化问题,利用半阈值追踪算法来求解,使得解满足1/2-范数最小的同时保证重建问题对参数的鲁棒性和加速重建时间。
附图说明
图1是本发明实施例提供的基于半阈值追踪算法的荧光分子断层成像重建方法流程图。
图2是本发明实施例提供的基于半阈值追踪算法的荧光分子断层成像重建方法的实现流程图。
图3是本发明实施例提供的用于仿真实验的数字鼠模型示意图。
图4是本发明实施例提供的重建算法与其它算法的参数比较图。
图5是本发明实施例提供的重建算法获得的重建结果示意图。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。
下面结合附图对本发明的应用原理作详细的描述。
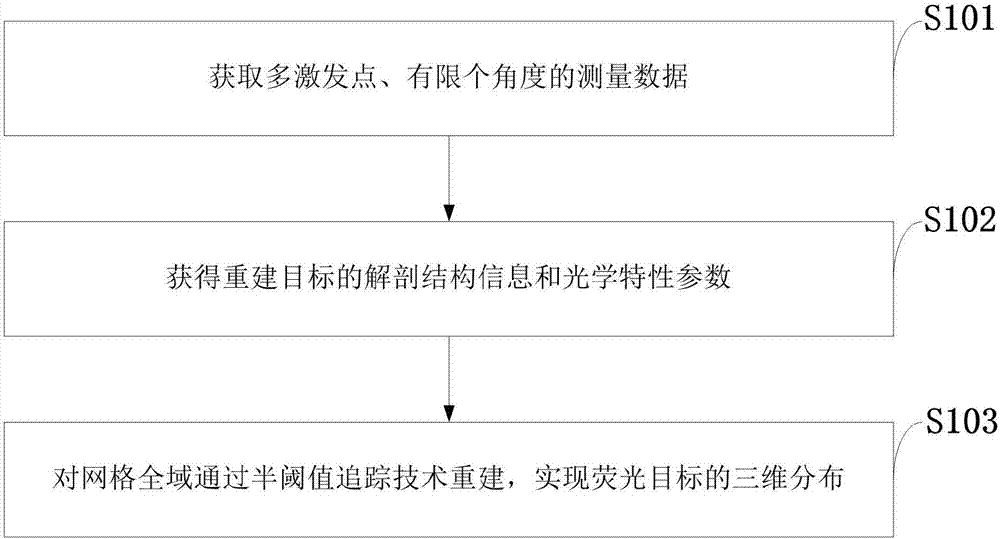
如图1所示,本发明实施例提供的基于半阈值追踪算法的荧光分子断层成像重建方法包括以下步骤:
s101:获取多激发点、有限角度的测量数据;
s102:获得重建目标的解剖结构信息和光学特性参数;
s103:对网格全域通过半阈值追踪技术重建,实现荧光目标的三维分布。
下面结合附图对本发明的应用原理作进一步的描述。
如图2所示,本发明实施例提供的基于半阈值追踪算法的荧光分子断层成像重建方法具体包括以下步骤:
(1)获取荧光测量数据:
1a)激发光源对固定在电控旋转台上的重建目标进行有限角度的透射式断层成像;
透射式断层成像,将激光器与光学检测仪器放置在成像目标的两侧,激光照射重建目标激发荧光目标发出荧光,荧光穿透成像目标被激光器对面的光学检测仪器检测到。
有限角度透射式断层扫描,用电脑控制电控旋转台等间隔旋转一定角度,一般大于90°(本例中选120°),激光器发射点状激光照射成像目标,一般转一个角度激发一次,采集一次荧光数据。
1b)使用光学检测仪器获得测量数据,获得光通量密度φm;
在步骤1a)中,将测量数据应用非接触式光学断层成像方法的生物体表面三维能量重建技术获取成像目标体表面的三维荧光数据分布。
(2)获得重建对象的解剖结构信息以及光学特性参数:
2a)重建对象的解剖结构信息
对计算机断层成像投影数据进行三维重建,并用3dmed软件预处理获得成像目标的三维体数据;采用3dmed软件中的人机交互式半自动化分割方法对体数据进行组织分割,获得成像目标的解剖结构;
2b)获取光学特性参数
利用解剖结构信息和应用基于生物组织特异性的光学三维重建方法的基于区域的扩散光学层析成像算法获得成像目标内各个组织的光学特性参数。
(3)利用amira软件对成像目标进行离散获得网格结构相关信息。
(4)基于光传输模型和有限元理论,将重建目标的解剖结构信息和光学特性参数作为先验信息,建立表面有限角度的荧光数据与重建目标内部荧光目标分布的线性关系。
4a)光传输模型,采用扩散近似方程来描述光在成像目标内的传输过程;
4b)根据有限元理论,并融合步骤(2)获得的重建目标的解剖结构信息和光学特性参数,将扩散近似方程离散,构建表面的测量数据与重建目标内部荧光目标分布的线性关系:
φm=ax;
其中a是系统矩阵,x是要求解的荧光目标三维分布与浓度,是非负的。
(5)将上述线性关系转化为1/2范数极小化问题:
λ是正则化参数。
(6)对步骤(5)中的模型,采用半阈值迭代技术求解,引入半阈值算子如下:
于是,半阈值迭代技术可以用表示为如下形式:
其中,b(x)=x+at(φ-ax)。
(7)为了减少(6)中的迭代次数,我们引入追踪方法,令b(x)≈x,于是每次迭代有如下过程:
(8)通过(7)中的迭代过程,得到第n步的重建结果xn。当||φ-axn||/||φ||≤1e-05或者||xn-xn-1||≤1e-08时,停止迭代。
上述步骤(5)-(8)为本发明的粗网格重建过程a。
(9)利用amira软件对成像目标进行离散获得网格尺寸较细的网格。
(10)显示结果,将步骤(9)的重建结果和成像目标的解剖结构进行图像融合,用tecplot软件进行显示。
下面结合重建结果对本发明的应用效果作详细的描述。
图3用于仿真实验的数字鼠模型。其中图包括了主要的几个器官,如心脏1,肺2,肝3,肌肉组织4,胃5,肾脏6。
图4是基于本发明的重建结果。重建目标的真实中心位置为(12,8,18)mm,算法获得的目标中心位置为(11.62,8.52,17.50)mm。位置误差为:
基于本发明的重建,其位置误差小,非零解个数少,重建时间短,迭代次数少,归一化均方误差小,相对噪声比大,是一种有效的针对有限投影角度的荧光分子断层成像重建算法。
以上所述仅为本发明的较佳实施例而已,并不用以限制本发明,凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!