一种高维不完整数据特征选择方法与流程
本发明涉及一种高维不完整数据特征选择方法,属于机器学习,数据挖掘技术领域。
背景技术:
随着数据获取技术的发展,高维数据广泛应用在于社交网络,图像处理,生物医学等领域中.然而在实际的数据的采集中,由于探测仪器的限制、数据敏感、样本破损等原因会导致采集数据的不完整,从而形成高维不完整数据.对于不完整数据的预处理通常采用删除和填补的方法,对于包含了大量冗余信息和噪声的高维数据,通常先采用特征提取和特征选择[6]对其进行降维.根据特征子集评估策略的差异,可将特征选择分为三类:filter模型、wrapper模型和embedded模型.filter模型仅依赖数据的内在特性来选择特征,而不依赖任何具体的学习算法指导.wrapper模型则需要一个预先设定的学习算法,将特征子集在其算法上的表现作为评估来确定最终的特征子集.embedded模型则是在学习算法的目标分析过程中包含变量选择,将此作为训练过程的一部分.共同之处是这三种模型都是通过相关性度量来选择特征,但是对于高维数据,得到的相关矩阵中会存在大量噪声.
随机矩阵理论(randommatrixtheory,rmt)通过比较随机的多维序列统计特性,可以体现出实际数据对随机的偏离程度,并揭示实际数据中整体关联的行为特征.随机矩阵理论是在原子物理中由wigner,dyson,mehta等人发展而来,在物理学,通讯理论,金融等方面应用非常广泛.laloux(1999)[9]等人研究了如何去掉金融相关系数矩阵的噪声,plerou(2002)等人详细研究了相关矩阵的特征值、特征向量的分布.
本文以随机矩阵理论为基础,提出一种特征选择方法,通过比较原始数据的相关矩阵和随机数据的相关矩阵在奇异值上的差异,去除原始相关矩阵的噪声,同时充分利用奇异值分解后的子矩阵来消除特征之间的冗余性,更好的实现特征选择.又根据熵概率选择,使这种方法能够应用于不完整数据.在分类准确率和运行时间上表明了本方法的高效性.
技术实现要素:
本发明针对现有技术的不足,本发明提供一种高维不完整数据特征选择方法。
本发明的是通过下述技术方案实现的:一种高维不完整数据特征选择方法,包括如下步骤:
(1)判断初始数据是否为完整数据;若为不完整数据,则转到步骤(2);若为完整数据,则转到步骤(3);
(2)采用不完整矩阵计算方法处理数据,具体为:
(2.1)假设现在有各个维度的数据,用1表示该数据项是完整的,用0表示该数据项是缺失的.计算每个维度的缺失率,接着通过下式计算缺失熵:
其中pi是每个维度的缺失率,h(x)表示缺失熵;
(2.2)h(x)越大说明不确定性越高,缺失率越接近0.5,h(x)的极值为0.5;依次算出每个维度的缺失熵;
(2.3)对结果进行加权平均;
(2.4)对每一个维度x的缺失值,p(忽略)=hmean(x),p(填补)=1-hmean(x);
(3)在高维数据中进行特征选择时,通过比较原始数据矩阵的相关矩阵和随机矩阵在奇异值上的差异,对相关矩阵进行去噪,其实现步骤如下:
(3.1)设有原始n×l数据矩阵d,其中特征集合f={f1,f2,…,,ft},类集合c={c1,c2,…,ck},通过(1)式构建互信息矩阵m,当k较小时,无法很好的满足随机矩阵的特征,因此需要对m进行增广,复制m次,即m=[m,m(m)],为了保持初始的行列比,这里m=((l-1)2/n*k)-1.
其中p(x,y)是特征和类别的联合分布,p(x)和p(y)分别是特征和类别的出现概率
(3.2)为了保证一般性,对矩阵m进行规范化,通过(2)式中心化,然后再通过(3)式进行标准化,得到矩阵md.接着根据(4)式计算得到t×t的特征相关矩阵c.
iij是矩阵m中第i行第j列的元素,maxii是第i行中最大的元素,minii是第i行中最小的元素。
(3.3)对c按(5)式进行奇异值分解.其中λ=diag(σ1,σ2,…,σr)且σ1≥σ2≥…σt>0,σi(i=1,2,…,r)为矩阵c的奇异值,这时称上式为矩阵c的奇异值分解式.
c=uλv(5)
(3.4)建立t×m随机矩阵,其变量服从均值为0,方差为1的正态分布,根据下式可以得到相关矩阵的最大特征值.
其中q是矩阵的行列比,即q=t/m,;
(3.5)根据随机矩阵理论,认为
cnew=uλnewv(6)
(3.6)对cnew进行奇异值分解的到unew和vnew,,cnew中的每个元素kij表示任意2个特征对初始类的相关程度,vnew中的每个元素eij是每个特征对新类的相关程度.
(3.7)对通过去噪后的相关矩阵进行特征选择,特征选择的目标是去除与类不相关的特征和相互冗余的特征.经过去噪的结果可知,共保留了j-1个奇异值,因此在这里共选择j-1个特征,因此可以根据(7)式计算每一个特征的重要度,其中f(i)表示第i个特征的重要度,得到集合f={f1,f1,…,fi},接着对f进行降序排序,选择前j-1个重要度最大的特征,从而完成特征选择;
其中iij是矩阵m的第i行第j列的元素,eij是(6)式中cnew奇异值分解后得到的右奇异矩阵vnew的第i行第j列的元素,kij是相关矩阵cnew的第i行第j列的元素。
本发明的有益效果:与现有技术相比,本发明提出基于随机矩阵理论的特征选择方法,其通过将相关矩阵中符合随机矩阵预测的奇异值去除,从而得到去噪后的相关矩阵和选择特征的数量,接着对去噪后的相关矩阵再进行奇异值分解,通过分解矩阵获得特征与类的相关性,根据特征与类的相关性和特征之间冗余性完成特征选择.。
附图说明
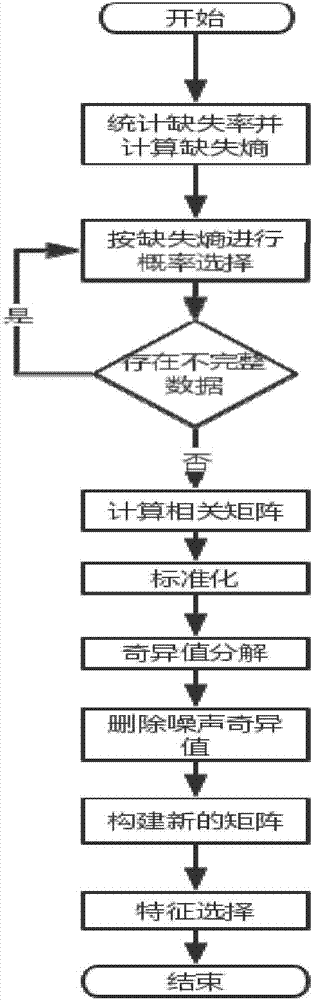
图1为本发明方法流程图。
具体实施方式
一种高维不完整数据特征选择方法,首先判断初始数据是否为完整数据;如果原始数据是不完整的,无法按照完整数据的方式来计算。需要通过以下步骤针对不完整矩阵计算,具体包括如下:
第一步:假设现在有各个维度的数据,用1表示该数据项是完整的,用0表示该数据项是缺失的.计算每个维度的缺失率,接着通过下式计算缺失熵:
第二步:h(x)越大说明不确定性越高,缺失率越接近0.5,h(x)的极值为0.5;依次算出每个维度的缺失熵;
第三步:对结果进行加权平均;
第四步:对每一个维度x的缺失值,p(忽略)=hmean(x),p(填补)=1-hmean(x);本发明方法的具体应用过程如下:
如果原始数据是不完整的,无法按照完整数据的方式来计算.因此本文提出了一个不完整随机矩阵计算方法.假设现在已经获取到了一个n×l训练数据矩阵,对于有数据缺失情况,需要更换计算方法.目前对于缺失值的处理通常有两种方法:删除和填补.考虑到缺失的数据可能是噪声或者是真实值.因此在对缺失值进行计算时,采取一种基于概率选择的计算方法.这里通过一个例子来说明.
表1数据缺失情况
假设现在有各个维度的数据,用1表示该数据项是完整的,用0表示该数据项是缺失的.计算每个维度的缺失率,例如humidity,其缺失率p=2/7,接着通过下式计算缺失熵:
其中pi是每个维度的缺失率,h(x)表示缺失熵;
计算出维度humidity的熵,p(humidity=缺失)=p,p(humidity=完整)=1-p,则h(humidity)有:
h(p)=-plog2p-(1-p)log2(1-p)
h(p)=0.3,h(p)越大说明不确定性越高,缺失率越接近;依次算出每个维度的缺失熵得:
表2缺失熵
表3加权平均结果
接着进行加权平均,根据hmean(x)的值进行概率选泽.即对于每一个维度x的缺失值,p(忽略)=hmean(x),p(填补)=1-hmean(x).
对于完整数据则执行以下步骤:
在高维数据中进行特征选择时,通过比较原始数据矩阵的相关矩阵和随机矩阵在奇异值上的差异,对相关矩阵进行去噪,其实现步骤如下:
第一步:设有原始n×l数据矩阵d,其中特征集合f={f1,f2,…,,ft},类集合c={c1,c2,…,ck},通过(1)式构建互信息矩阵m,当k较小时,无法很好的满足随机矩阵的特征,因此需要对m进行增广,复制m次,即m=[m,m(m)],为了保持初始的行列比,这里m=(l2/n)-1.
其中p(x,y)是特征和类别的联合分布,p(x)和p(y)分别是特征和类别的出现概率
第二步:为了保证一般性,对矩阵m进行规范化,通过(2)式中心化,再通过(3)式标准化,得到矩阵md.接着根据(4)式计算得到t×t的特征相关矩阵c.
iij是矩阵m中第i行第j列的元素,maxii是第i行中最大的元素,minii是第i行中最小的元素。
第三步:对c按(5)式进行奇异值分解.其中λ=diag(σ1,σ2,…,σr)且σ1≥σ2≥…σt>0,σi(i=1,2,…,r)为矩阵c的奇异值,这时称上式为矩阵c的奇异值分解式.
c=uλv(5)
第四步:建立t×m随机矩阵,其变量服从均值为0,方差为1的正态分布,根据下式可以得到相关矩阵的最大特征值.
其中q是矩阵的行列比,即q=t/m,;
第五步:根据随机矩阵理论,认为
cnew=uλnewv(6)
第六步:对cnew进行奇异值分解的到unew和vnew,cnew中的每个元素kij表示任意2个特征对初始类的相关程度,vnew中的每个元素eij是每个特征对新类的相关程度.
第七步:对通过去噪后的相关矩阵进行特征选择,特征选择的目标是去除与类不相关的特征和相互冗余的特征.经过去噪的结果可知,共保留了j-1个奇异值,因此在这里共选择j-1个特征,因此可以根据(6)式计算每一个特征的重要度,其中f(i)表示第i个特征的重要度,得到集合f={f1,f1,…,fi},接着对f进行降序排序,选择前j-1个重要度最大的特征,从而完成特征选择.
其中iij是矩阵m的第i行第j列的元素,eij是(6)式中cnew奇异值分解后得到的右奇异矩阵vnew的第i行第j列的元素,kij是相关矩阵cnew的第i行第j列的元素。
(3)实验
(3.1)实验数据集
为了说明本文提出的特征选择方法的有效性,通过分类实验来验证。选取uci机器学习知识库上10个数据集进行实验。表4是对数据集的描述,数据集中的实例数从13910到101,特征从649到17,分布范围很宽广。
表4实验中用到的数据集
(3.2)实验结果与分析
实验在win7_64系统,8gb内存,主频2.93ghz的corei7-870的pc上运行,采用python3.6,scikit-learn工具包。使用经典的mdl[11]方法对数据进行离散化,采用1-n,cart,
表51-nn分类器准确率
表6cart分类器准确率
表7
表8选择特征的个数
根据表5.6.7,可以看出本文所提的特征选择方法在三个分类器上整体胜率是63.3%,在平均准确率上的胜率是100%。当特征数大于100时,整体胜率是90.4%,在高维特征选择表现优异。相对于表现较好的fcbf,本方法在平均准确率上领先其1.86%。同时所提出的优化方法rmfs-o相对于rmfs在特征数大于300时,平均准确率领先1.38%。根据表8,本方法在平均特征选择数量上明显优于对比方法,相对于最好的fcbf,平均缩小了44.4%的数据规模。当特征数大于300时,类大于10时,相对于对比方法,平均缩小了59.7%的数据规模。
- 还没有人留言评论。精彩留言会获得点赞!