五轴数控机床加工中基于精细积分的球头铣刀颤振稳定域叶瓣图建模方法与流程
本发明属于机械制造技术领域,涉及到五轴数控机床铣削切削过程中颤振稳定域建模方法,尤其是球头铣刀在五轴数控机床铣削切削过程中颤振稳定域叶瓣图建模方法。
背景技术:
机械制造业作为国家经济增长支柱,已经发展了上百年,建立了比较系统的理论体系,积累了丰富的实践经验,但随着科学技术水平的提高,迫切的需要其向高速、高效和高精度方向发展。
高速铣削加工是先进制造技术中最重要的基础技术之一,是目前最重要、应用最普遍的加工方式,然而在高速铣削过程中不合适的切削参数导致的切削颤振严重地影响到了加工效率、精度、质量以及稳定性,是制约高速铣削技术快速发展的关键因素。
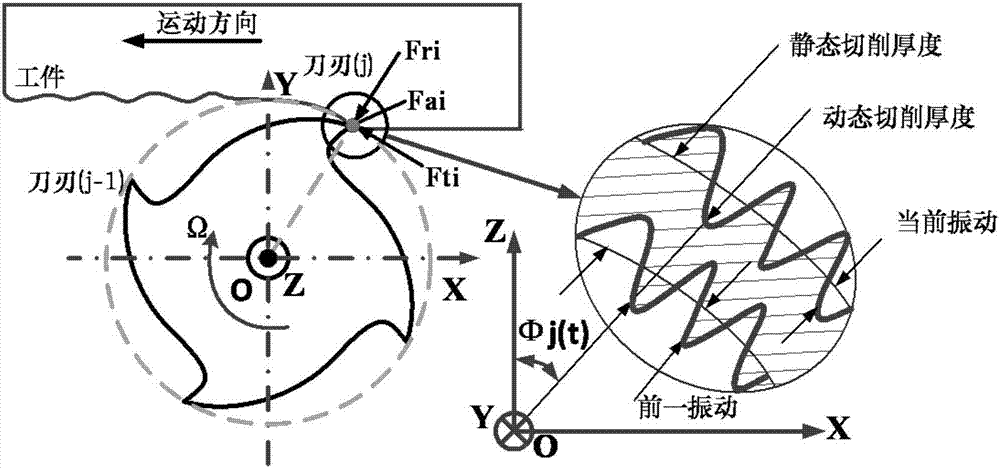
国内外学者对切削颤振进行了大量探索,研究了多种颤振形成的机理,其中再生型颤振是人们认为产生切削过程中产生颤振最直接、最根本的原因。如图1所示,再生型颤振理论指出,由于机床结构振动,当刀具进行切削时,工件的已加工表面会留下表面振纹,当刀具再一次切削到这些遗留有振纹的工件表面时,瞬时切削厚度由名义切削厚度和动态切削厚度叠加组成,这种切削厚度的变化引起切削力的波动,反过来又引起切削刀具和工件之间的相对振动,使刀具和工件在切削过程中产生振动位移,从而再次在工件已加工表面留下振纹,根据前后两次振纹之间的相位差,在靠近但不等于加工系统主结构模态的颤振频率处,随着加工系统的切削厚度不断增长,造成切削力和振动位移的不断上升现象,形成强烈的自激振动,这种自激振动就是再生颤振,图2为再生颤振机理模型。
避免切削颤振最有效办法是在加工前构建铣削颤振稳定域叶瓣图,即在给定切削条件下,绘制出轴向临界切削深度随主轴转速变化的函数关系。叶瓣图的构建能够为加工前切削参数的选择提供指导,可以有效防止加工中颤振的发生。而球头铣刀是典型的点接触加工,具有很好的法矢自适应性,是高速铣削加工中应用最广的刀具之一,因此构造出针对球头铣刀加工过程中的稳定性叶瓣图意义重大。
目前,国内外还没有针对球头铣刀在五轴数控机床加工过程中的颤振稳定域叶瓣图建模方法。有部分学者对三轴数控机床上球头铣刀颤振稳定域叶瓣图建模方法进行了研究,其中具有代表性的有:李忠群等人提出的基于龙格库塔的时域求解法;dingh等人提出的全离散时域求解法;limingzhen等人提出的完全离散时域数值求解法。但是不论是龙格库塔法,全离散法,还是改进的完全离散法本质上都属于差分类方法,它们的优点是易于实现,但差分引起的误差很难从根本上消除。同时,五轴数控机床和三轴数控机床的加工方式不同,刀具姿态不同,故球头铣刀在三轴数控机床的建模方法并不能适用于其在五轴数控机床上;因此如何在更先进的五轴数控机床上对球头铣刀进行高精度的颤振稳定域叶瓣图构建将是一个亟待解决的问题。
技术实现要素:
为了解决现有技术存在的问题,本发明提供一种五轴数控机床加工中基于精细积分的球头铣刀颤振稳定域叶瓣图建模方法。
本发明的技术方案为:
一种五轴数控机床加工中基于精细积分的球头铣刀颤振稳定域叶瓣图建模方法,包括以下步骤:
步骤一,建立球头铣刀刀具-工件动力学方程;
步骤二,求解球头铣刀刀齿上的动态切削力ftx(t)和fty(t);
步骤三,五轴数控机床平面加工中球头铣刀与工件的接触区域半解析建模;
步骤四,精细积分法对刀具-工件动力学方程时域数值求解;
步骤五,叶瓣图构建。
本发明的有益效果为:运用精细积分法对铣削系统二阶动力学方程进行高精度时域数值求解,克服了传统数值求解法不能同时兼顾计算精度、计算效率和稳定性的弊端;精准识别出球头铣刀存在前倾角和侧倾角时与工件接触区域边界的投影方程,在单齿切削周期内球头铣刀视为圆弧切削的基础上,通过球头铣刀与工件的接触区域投影边界方程和切削刃不同时刻的投影方程的关系,确定出时域数值方程中所需要的瞬时参与切削的刀刃数目和参与切削刀刃的实际切削部位,利用floquet定理获得了不同转速下临界切削深度,构建出了球头铣刀存在前倾角和侧倾角时的颤振稳定域叶瓣图。
附图说明
图1是球头铣刀铣削过程中再生颤振发生机理示意图。
图2是球头铣刀铣削过程中再生颤振机理模型。
图3是球头铣刀铣削动力学模型。
图4是球头铣刀螺旋切削刃几何模型。
图5是球头铣刀-工件接触区域示意图。
图6是球头铣刀-工件接触区域边界组成示意图。
图7是球头铣刀三维坐标x0-y0-z0建立示意图。
图8是推导出刀具前倾角为α,侧倾角为零时的刀位点和刀触点示意图。
图9是球头铣刀三维坐标x1-y1-z1和x-y-z建立过程示意图。
图10是球头铣刀三维坐标xp-yp-zp建立过程示意图。
图11是球头铣刀三维坐标xf-yf-zf建立过程示意图。
图12是球头铣刀三维坐标xm-ym-zm建立过程示意图。
图13是三维坐标xm-ym-zm示意图。
图14是b号投影线求解示意图。
图15是m点示意图。
图16是n点示意图。
图17是d号线投影求解中沿y1轴等间距取值示意图。
图18是d号线投影方程求解过程示意图。
图19是接触区域在xm-ym坐标系投影示意图。
图20是第一条切削刃投影0-t5时刻位置。
图21是tp=0时刻,切削刃参与切削情况。
图22是tp<t1时刻,切削刃参与切削情况。
图23是t1<tp<t2时刻,切削刃参与切削情况。
图24是t2<tp<t3时刻,切削刃参与切削情况。
图25是t3<tp<t4时刻,切削刃参与切削情况。
图26是t4<tp<t5时刻,切削刃参与切削情况。
图27是t5<tp<t6时刻,切削刃参与切削情况。
图28是t6<tp<t7时刻,切削刃参与切削情况。
图29是轴向切削深度小于l_jg时的接触区域在xm-ym坐标系下投影的边界组成。
图30是叶瓣图构建流程图。
具体实施方式
以下结合技术方案和附图详细叙述本发明的具体实施方式。
五轴数控机床上加工中基于精细积分的球头铣刀颤振稳定域叶瓣图建模方法,包括以下步骤:
步骤一,建立球头铣刀刀具-工件动力学方程
将球头铣刀刀具-工件系统简化为如图3所示的二自由度系统,仅考虑进给方向x和法向y方向的刀具振动因素,建立如下所示的动力学方程:
其中,mtx,ξx,ωnx分别是为刀具系统x方向的模态质量,阻尼系数,固有频率;mty,ξy,ωny分别是为刀具系统y方向的模态质量,阻尼系数,固有频率;ftx(t)和fty(t)分别为在x,y方向上作用在铣刀上的动态切削力。
步骤二,求解球头铣刀刀齿上的动态切削力ftx(t)和fty(t)
2.1建立球头铣刀刀刃几何模型
如图4所示,建立球头铣刀切削刃曲线几何模型,由于每个切削微元与其所对应的轴向角存在一一映射关系,故切削微元坐标值可以表示为关于轴向角的函数,式(2)为第j刀刃上第i个切削微元坐标表达式。
其中,r为球头铣刀半径;μ切削刃螺旋角;t为切削过程中的时间(s);k为第j刀刃上第i个切削微元的轴向接触角,在一个切削刃上所能取值范围为[0,π/2];ψji(k)为第j刀刃上第i个切削微元径向滞后角;φ10(t)为第一个切削刃端点处转动的角度,n为刀具转速(r/min);φji(t)为第j刃上的第i个微元处瞬时径向接触角;nf为切削刃数目;xji(t),yji(t),zji(t)表示球头铣刀第j刀刃上第i个切削微元在所建立的坐标系下的坐标值。
2.2球头铣刀瞬时动态切削力计算
球头铣刀第j刀刃上第i个切削微元(轴向角为k)所受的切向力dft,ji(φji(t),k)、径向力dfr,ji(φji(t),k)、轴向力dfa,ji(φji(t),k)表示为:
其中,h(φji(t),kji)为第j刀刃上第i个切削微元瞬时切削厚度,ktc为切向力系数,krc为径向力系数,kac为轴向力系数;db=r·dk,r为球头铣刀半径。
2.3瞬时动态切削厚度计算
刀具瞬时铣削厚度由两部分组成,一部分是瞬时静态切削厚度,另一部分是瞬时动态切削厚度,瞬时静态切削厚度与颤振无关,故将其忽略。
仅考虑刀具x和y方向的振动,球头铣刀第j刀刃上第i个切削微元(轴向角为k)的瞬时动态铣削厚度为:
其中,x(t)-x(t-t),y(t)-y(t-t)表示当前时刻t和前一个刀齿切削(t-t)时刻在x和y方向的动态振动矢量;t为时滞周期,在高速切削条件下,时滞周期等于单齿切削周期,即时滞周期
2.4刀具瞬时动态切削力计算
通过坐标变换,获得第j刀刃上第i个切削微元x,y方向动态切削力:
由式(3),式(4)和式(5)得到如下结果:
其中,axx,ji(t)、axy,ji(t)、ayx,ji(t)、ayy,ji(t)如下所示。
确定每个切削刃在t时刻的参与切削片段的数目和每个参与切削的片段所对应的最大轴向角和最小轴向角,通过公式(6)就得到球头铣刀上的动态切削力。
其中,
步骤三、五轴数控机床平面加工过程中球头铣刀与工件接触区域的半解析建模
球头铣刀和工件的接触区域是指在加工过程中刀具切入工件的区域。高速铣削条件下,在单齿切削周期内,球头铣刀可视为圆弧切削,因此铣刀-工件接触区域蕴含着式(6)中所需要的单齿切削周期内铣刀瞬时参与切削的刀刃数目和参与切削刀刃的实际切削部位等信息。
3.1进行刀具路径规划,设置加工参数
球头铣刀在五轴数控机床上进行平面铣削,球头铣刀球头半径为r,前倾角为α度,侧倾角为β度,相邻切削刀轨间距为l_xl,轴向切削深度为l_jg。
3.2确定前倾角为α度,侧倾角为β度时球头铣刀与工件接触区域边界组成,将接触区域边界方程的求解问题转化为这些边界在垂直于刀具轴线平面的投影方程的求解问题;
如图5所示,前倾角为α,侧倾角为β度时球头铣刀与工件的接触区域主要由图6中所示的a,b,c,d四条线组成,其中,a号线为铣刀球头与工件加工表面的交线,b号线为铣刀球头与工件过渡表面的交线,c号线为本次走刀与上一次走刀在已加工表面留下的加工残余而形成的线,d号线为铣刀球头与上一次走刀留下的加工痕迹的交线。另外e号线为上一次走刀在工件加工表面留下的加工痕迹。
在切削静力学和切削动力学模型中,确定刀刃某一时刻参加切削的上下边界时都是在二维平面上进行的,因此根据球头铣刀球头部分沿垂直刀轴的方向具有单调分布的特点,将a,b,c,d四条线求解问题转化为它们在垂直于刀具轴线平面的投影方程的求解问题。
3.3由刀具前倾角和侧倾角为零度时的三维直角坐标系x0-y0-z0推导出刀具前倾角为α,侧倾角为零度时的三维直角坐标系x-y-z
如图7所示,建立刀具前倾角和侧倾角都为零度时的三维直角坐标系x0-y0-z0,其中刀具顶点为原点o0,刀轴线为z0轴,x0轴与刀具进给方向相同。下面将由x0-y0-z0推导出刀具前倾角为α,侧倾角为零度时的三维直角坐标系x-y-z,由于侧倾角都为零度,故只需要在x0-z0平面讨论即可。
如图8所示,在x0-z0平面内,将z0轴以o0为原点,顺时针倾斜α度(从y0负方向向原点看,α值为正数,顺时针;α值为负数,逆时针,此处以α为正进行阐述),倾斜之后的轴线就是刀具前倾角为α度,侧倾角为零度时的刀具轴线,该直线方程z0=tan(90-α)×x0与直线z0=r的交点cir_0,即为刀具前倾角为α度,侧倾角为零度时的球心,经计算cir_0的坐标为xcir_o=r/tan(90-α),zcir_0=r。
以cir_0为原点,r为半径建立圆的方程(x0-xcir_0)2+(z0-ycir_0)2=r2,此圆方程与x0轴的切点即为前倾角为α度,侧倾角为零度时的球头铣刀的刀触点dc_0,经计算dc_0的坐标xdc_0=r/tan(90-α),zdc_0=0。
(x0-xcir_0)2+(z0-ycir_0)2=r2方程与z0=tan(90-α)×x0方程两个交点中y0值较小的点即为前倾角为α度,侧倾角为0度时的球头铣刀的刀位点dw_0。经计算xdw_0=r/tan(90-α)-r×sinα,zdw_0=r-r×cosα。
如图9所示,以dc_0为原点,建立三维直角坐标系x1-y1-z1,其中,x1-z1平面与x0-z0平面相重合,x1与x0相互重合且方向相同,y1与y0平行且方向相同。
如图9所示,以dw_0为原点,方程z0=tan(90-α)×x0为z轴建立三维直角坐标系x-y-z,其中x-z平面与x0-z0平面相重合,y与y0平行且方向相同,z轴正方向为远离工件。x-y-z坐标系下,铣刀球头轮廓方程x2+y2+(z-r)2=r2。
3.4通过x-y-z三维坐标系,建立刀具前倾角为α,侧倾角为β度时的xm-ym-zm坐标系,获取x-y平面上点与xm-ym平面上点的关系
如图10所示,将x-y-z坐标系中的x-y平面沿着z轴正方向平移r距离,使坐标系的原点o与铣刀球心重合,获得新的坐标系xp-yp-zp。其中xp-yp-zp坐标系中的xp轴与x轴相互平行,且方向相同;yp轴与y轴相互平行,且方向相同;zp轴与z轴相互重合,且方向相同。
由xp-yp-zp坐标系获得方式可知,xp-yp平面中的点(xp,yp)与x-y平面中的点(x,y)的关系为:
xp=x,yp=y(7)
如图11所示,以xp轴为轴线,将yp-zp平面逆时针旋转β度(xp轴正半轴向原点看,β值为正数,顺时针;β值为负数,逆时针,以下以β为负值进行阐述),旋转之后,yp轴变为yf轴,zp轴变为zf轴,形成一个新的坐标系xf-yf-zf,其中xf与xp轴重合且方向相同。
由xf-yf-zf坐标系获得方式可知,xp-yp-zp坐标系中点(xp,yp,zp)与xf-yf-zf坐标系中的点(xf,yf,zf)关系为:
令zf=zp=0,则可得:
xf=xp,yf=ypcosβ(8)
如图12所示,将坐标系xf-yf-zf中的xf-yf平面沿着zf负方向平移r距离,得到xm-ym-zm坐标系,其中,xm轴与xf轴相互平行,且方向相同;ym轴与yf轴相互平行,且方向相同;zm轴与zf轴相互重合,且方向相同。如图13所示,xm-ym-zm坐标系的原点就是前倾角为α度,侧倾角为β度时球头铣刀的顶点,zm轴就是前倾角为α度,侧倾角为β度时球头铣刀的轴线,a,b,c,d四条边界的求解问题转化为它们在xm-ym平面的投影方程的求解问题。
由xm-ym-zm坐标系获得方式,可知xm-ym平面中的点(xm,ym)与xf-yf平面中的点(xf,yf)的关系为:
xm=xf,ym=yf(9)
由公式(7),(8)和(9)可得x-y平面上点与xm-ym平面上点的关系:
xm=x,ym=ycosβ(10)
经过以上推导可知,前倾角为α度,侧倾角为零度时和前倾角为α度,侧倾角为β度时,铣刀球头的位置并没有变化,刀触点没有变化,只是刀轴线变化了,刀位点发生了变化,也即目标坐标系由x-y-z变成了xm-ym-zm,这主要是由铣刀球头的几何特性所形成的。
由式(10)可知xm-ym平面上点与x-y平面上点的关系,因此,a,b,c,d四条线边界曲线在xm-ym坐标系下的投影方程的求解问题可以转化为这四条线边界线在x-y坐标系下的投影方程的求解问题。
3.5确定a,b,c,d,e四条线在x-y坐标系下的投影方程
3.5.1a号线在x-y坐标系下投影方程求解过程
a号线为铣刀球头与工件加工表面的交线。如图8所示,工件加工表面在x-y-z坐标系下的方程需要通过x0-y0-z0坐标系与x-y-z坐标系关系的获得。
如图9所示,在x0-z0坐标系下,在工件加工表面任取a(xa0,za0)、b(xb0,zb0)两点,由于工件加工面为平面,故za0=zb0=l_jg。通过x–z坐标系与x0-z0坐标系的关系,可获得a、b两点在x–z坐标系的值(xa,za),(xb,zb),具体获取方式如下:
获取a、b在x–z坐标系下坐标之后,计算出经过a、b两点在x–z坐标系下的直线方程z=kx+b,其中
在x-y-z下,将工件加工表面方程z=kx+b与铣刀球头方程x2+y2+(z-r)2=r2方程联立,即可得到a号线在x-y二维坐标系下投影方程x2+y2+(kx+b-r)2=r2。
3.5.2b号线投影方程求解过程
b号线为球头铣刀垂直于进给方向的轮廓圆截面与工件过渡表面的交线,如图14所示,此圆投影到x-y二维坐标系下为一椭圆,椭圆方程为
3.5.3c号线投影方程求解过程
c号线为本次走刀与上一次走刀在工件已加工表面留下的加工残余而形成的线,如图15所示,在y1-z1坐标系下,获得铣刀球头投影方程y12+(z1-r)2=r2,将其沿着y1负方向平移l_xl,得到方程(y1+l_xl)2+(z1-r)2=r2,即为与本次刀触点相对应的上一次加工时的铣刀球头轮廓方程。两圆交点m所对的y1值为-l_xl/2,即为c号线在x1-y1二维坐标系下的投影,由于x-y-z坐标系与x1-y1-z1坐标系的x-z平面与x1-z1平面相重合,y轴与y1轴相互投影方程平行,故c号线在x-y二维坐标系下的投影方程为y=-l_xl/2。
3.5.4d号线求解过程
d号线投影方程求解过程同a号和e号线投影方程有关,在求解d号线投影方程之前,先确定e号线投影方程。
1)e号线投影方程求解过程
e号线为上一次走刀在工件加工表面留下的加工痕迹。如图15所示,在y1-z1坐标系下,将z1=l_jg带入到与本次刀位点相对应的上一次加工时的铣刀球头轮廓方程(y1+l_xl)2+(z1-r)2=r2中,得到的最大的y1即为e号线在x1-y1坐标系下的投影,经计算该值为
2)d号线投影方程求解过程
图16中的d号线上的n点在x-y坐标系下的投影可由a号线和e号线在x-y坐标系下投影方程联立得到,经计算n点x值满足方程
利用分层思想可知,d号线上的其它点可以认为是不同轴向切削深度所对应的a号线与e号的交点,因此将n点坐标中的l_jg用变量k_v替换,可得
如图17示,k_v最大取值为l_jg,最小取值为e号线在y1-z1坐标系投影所对应的z1坐标,即m点所对用的z1值
如图17所示,d号线在x1-y1平面投影所对应的最大y1值为
3.6确定a,b,c,d在xm-ym坐标系下的投影方程
利用式(10)x=xm,y=ym/cosβ分别替换掉a,b,c,d在x-y坐标系下投影方程中的x,y,获得的新的方程就是a,b,c,d在xm-ym坐标系下的投影方程,如图19示,它们共同围成的区域即为前倾角为α,侧倾角为β时球头铣刀与工件接触区域在xm-ym坐标系下的投影。
步骤四、精细积分法对刀具-工件动力学方程时域数值求解
4.1精细积分法对刀具-工件动力学方程时域数值分解
由式(6)可将式(1)表示为如下形式:
将式(11)表示为如下所示的哈密顿系统:
其中,
将式(12)中a(t)v(t)-a(t)v(t-t)用f(t)来表示,则对于非齐次方程(12),由常微分理论可知,一般解为:
将时滞周期t均分为m份,即t=m·τ,在[tp,tp+1]中,将f(t)表示为如下形式:
f(t)=r0+r1(t-tp)(14)
其中,r0=f(tp)=a(tp)v(tp)-a(tp)v(tp-m·τ)
由式(13)和式(14)可将v(tp+1)表示
v(tp+1)=t·[v(tp)+a0-1(r0+a0-1r1)]-a0-1(r0+a0-1r1+r1·τ)(15)
其中,
由于
由式(16)和式(17)可知,
因此,用n次矩阵相称就能得到t中的非单位矩阵部分,即
将r0和r1进一步分别表示为
r0=apvp-apvp-m(20)
将(20)和(21)带入到式(15)中,可得:
其中,mm=ta0-1-a0-1,nn=ta0-2-a0-2-a0-1τ
若(i-nn/τ·ap+1)可逆,则式(22)可表示为
其中,
4.2axx,p,axy,p,ayx,p,ayy,p和axx,p+1,axy,p+1,ayx,p+1,ayy,p+1确定方法
下面以nf=2为例,来阐述axx,p,axy,p,ayx,p,ayy,p方法。在tp时刻,按照公式(2)将球头铣刀全部切削刃投影到第三部分所建立的xm-ym坐标系下,其中
由铣刀刀齿数和构建出的刀具-工件的接触区域可知在时滞周期内的任意时刻,只有一条切削刃参与切削,设此切削刃为第一条切削刃。如图20所示,该切削刃在单齿切削周期内到达与b号线相切位置;b投影线与a投影线交点位置;与d号线相切位置;a投影线与d投影线交点位置;d投影线与c投影线交点位置;c投影线与b投影线交点位置;时滞周期切削结束的时刻分别记为t1,t2,t3,t4,t5,t6,t7。
当tp=0时,如图21所示,第一条切削刃没有参与切削,当tp在0-t1时间内,如图22所示,第一条切削刃没有参与切削,此时kmax,1和kmin,1值都为零;当tp在t1-t2时间内,如图23所示,第一条切削刃与b号线投影线相交,两个交点所对应的轴向角的最大值即为tp时刻该切削刃在式(24)中所对应的kmax,1,最小值为tp时刻该切削刃在式(24)中所对应的kmin,1。同理,可以确定tp分别在t2-t3,t3-t4,t4-t5,t5-t6时间段内,第一条切削刃所对应kmax,1和kmin,1值,具体如图24-图27所示;当tp在t6-t7时间内,如图28所示,第一条切削刃没有参与切削,此时kmax,1和kmin,1值都为零。
确定出各个切削刃在tp参与切削的最大轴向角和最小轴向角之后,通过式(24)可得到axx,p,axy,p,ayx,p,ayy,p值。
通过以上步骤可以得到tp+1时刻时axx,p+1,axy,p+1,ayx,p+1,ayy,p+1值。
步骤五、叶瓣图构建
5.1切削稳定性判定方法
建立系数矩阵cp,该矩阵满足离散映射:
vp+1=cpvp(25)
vp是个(2m+4)维的向量:
矩阵cp为(2m+4)维矩阵:
pk为4×4矩阵等于公式(23)中的(i-nn/τ·ap+1)-1(t+mm·ap-nn/τ·ap),rk1为4×2矩阵,等于式公式(23)中的-(i-nn/τ·ap+1)-1nn/τ·ap+1的前两列,rk2为4×2矩阵,等于式(23)中的(i-nn/τ·ap+1)-1(nn/τ·ap-mm·ap)的前两列。
通过使用一系列离散cp(p=0,1,2…,m-1),构建时滞周期t内的过渡矩阵φ,亦即:
vp=φv0(28)
式中,φ定义为:φ=cm-1cm-2…c1c0。
由floquet理论可知,传递函数φ所有特征值模的最大值小于1,等于1和大于1,分别表示在该刀具转速n和轴向切深l_jg下,切削处于稳定状态,临界临界状态和不稳定状态。
5.2叶瓣图构建
主轴转速不变,在[0,l_jg]范围内不断改变轴向切深,通过5.1中的方法,获得该转速下所对应的临界轴向切深。改变轴向切深后的接触区域投影边界中只有a号线投影方程变化,b号线和c号线投影方程仍与l_jg时相同,具体如图29所示。
改变主轴转速,获得不同主轴转速在[0,l_jg]范围内所对应的临界轴向切深。最终,构建出临界轴向切深随主轴转速变化的函数关系,即为颤振稳定域叶瓣图,整个流程如图30所示。
- 还没有人留言评论。精彩留言会获得点赞!