基于可信度的湿法冶金浓密机的故障诊断方法与流程
本发明属于湿法冶金技术,尤其涉及一种基于可信度的湿法冶金浓密机的故障诊断方法。
背景技术:
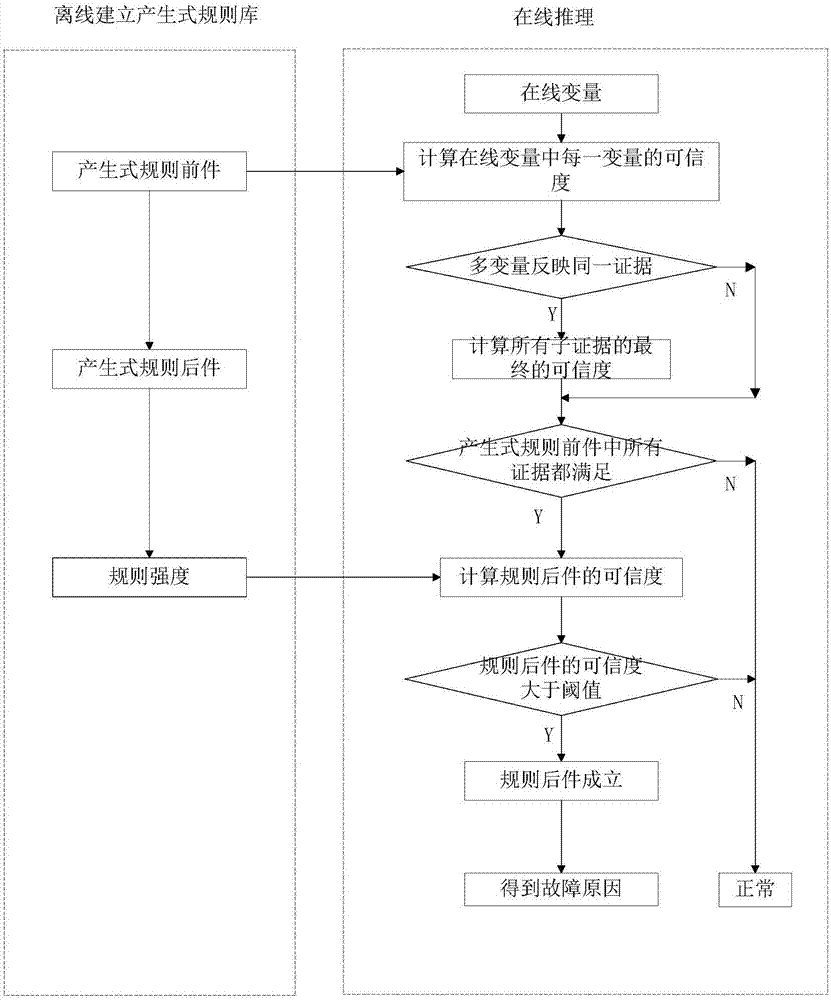
:随着我国工业化进程的发展,资源问题成为制约我国发展的主要问题之一。矿产资源作为工业原料的主要来源,在经济社会发展中起着基础性的作用。由于对矿产资源的粗放利用和大量消耗,致使我国面临矿产资源严重紧缺的难题,高品位矿产资源的储量正日益减少,形势十分严峻。我国低品位矿产资源的储量丰富,从贫、细、杂矿石中提取矿产资源成为了未来发展的必然趋势,如何经济高效的利用低品位矿产资源对于我国经济社会的可持续发展具有重要意义。随着矿石品位的不断降低和对环境的要求日益严格,湿法冶金在低品位矿产资源的开发和利用中起着重要的作用。湿法冶金流程浓密洗涤是利用重力进行固液分离的过程,可以节省大量能源,主要指标是底流浓度。浓密洗涤过程是湿法冶金过程的一道关键工序。在工业生产中,通常将固体物料溶于溶剂中,将不同组分进行分离,即湿法分选,选出的产物为固液两相的悬浮液,为了得到含水较少的固体产物和基本不含固体的水,大多数情况下都要进行固液分离。目前,浓密机洗涤过程的故障诊断大多数依靠操作人员主观实现,自动化水平较低。浓密洗涤过程工艺复杂、生产环境恶劣,且具有大惯性、大时滞、影响因素多等特点,加之人为主观因素的影响,很难实现准确的故障诊断。在实际过程中,很多变量是实时变化且随机性大,而且变动频繁,这使得实现对浓密洗涤过程的故障诊断更加困难。技术实现要素:针对现有存在的技术问题,本发明提供一种基于可信度的湿法冶金浓密机的故障诊断方法,该方法可以预先建立专家或操作人员的诊断经验对应的规则库,进而采用该规则库中的规则及基于可信度的不确定性推理模型进行推理分析,获取故障结果的概率,以便根据概率调整在实际操作,有效降低事故发生率,提高生产安全性。本发明的基于可信度的湿法冶金浓密机的故障诊断方法,包括:获取湿法冶金浓密机的在线变量;根据在线变量,确定每一变量的模糊维度;所述模糊维度为预先建立的专家规则库中的规则前件包括的变量对应的模糊维度;针对每一个变量及该变量的模糊维度,采用模糊隶属度函数获取该变量所属模糊维度的可信度;基于可信度的不确定性推理模型结合专家规则库中的规则,对每一变量的可信度进行推理分析,得到故障结论可信度;将故障结论可信度与预设阈值进行比较,根据比较结果确定是否发生故障,以及发生故障的概率。可选地,获取湿法冶金浓密机的在线变量的步骤之前,所述方法还包括:离线获取预设时间段内湿法冶金浓密机的历史变量;结合湿法冶金领域专家及相关操作人员的先验知识、获取多个用于进行浓密机故障诊断的专家规则;根据多个用于进行浓密机故障诊断的专家规则,建立专家规则库;其中,每一浓密机故障诊断专家规则包括:通过变量的模糊维度表达的规则前件、通过结论表达的规则后件、说明结论可信度的规则强度;每一个规则的规则前件、规则后件和规则强度具有对应关系;所述规则前件中的变量具有至少一个模糊维度。可选地,基于可信度的不确定性推理模型结合专家规则库中的规则,对每一变量的可信度进行推理分析的步骤之前,所述方法还包括:判断在线变量中多个变量是否反映同一个证据,如果是,则将反映同一个证据的多个变量的可信度进行逻辑组合;其中,证据为与专家规则库中的每一规则前件对应,且属于在线变量反映的规则前件;相应地,基于可信度的不确定性推理模型结合专家规则库中的规则,对每一变量的可信度进行推理分析的步骤,包括:基于可信度的不确定性推理模型结合专家规则库的规则对逻辑组合的多变量的可信度进行推理分析。可选地,判断在线变量中多个变量是否反映同一个证据的步骤,包括:查找在线变量中每一变量所匹配的规则在专家规则库中的规则标识;相应地,将反映同一个证据的多个变量的可信度进行逻辑组合的步骤,包括:将属于同一规则标识的多个变量的可信度按照该规则标识中各个变量的逻辑组合关系进行逻辑组合。可选地,采用模糊隶属度函数获取该变量的可信度,包括:根据下述公式,获取每一变量的可信度;其中,k为经验系数,xmean为预先设定的待分析的变量的正常范围平均值,x为待分析的变量,μcf(x)为待分析的变量的可信度。可选地,将故障结论可信度与预设阈值进行比较,根据比较结果确定是否发生故障及发生故障的概率,包括:若故障结论可信度大于预设阈值,则确定发生故障,且将故障结论可信度作为发生故障的概率,以及根据故障结论可信度确定故障发生可能的原因;若故障结论可信度小于等于预设阈值,则确定不发生故障,结束。可选地,湿法冶金浓密机的在线变量包括:直接测量的反映浓密机生产状态的变量,以及通过直接测量的变量分析的反映浓密机生产状态的变量;所述直接测量的变量包括:矿浆压力一、矿浆压力二、中心搅拌电机电流、压滤机前缓冲槽液位和/或渣浆泵电流;通过直接测量的变量分析的反映浓密机生产状态的变量包括:压滤机前缓冲槽液位变化率、耙底压力、底流流量和/或底流浓度。可选地,基于可信度的不确定性推理模型中,产生式规则的形式为:ifethenhwithcf(h/e)其中,e表示一个简单前提,或多个简单前提逻辑组合的逻辑组合前提,h为一个或多个结论,cf(h/e)为基于所述e发生h的可信度;相应地,采用产生式规则的形式表示专家规则库的中规则前件、规则后件、规则强度的对应关系,则为:e表示每一规则的规则前件中的变量的模糊维度,h为该规则的规则后件中的结论,cf(h/e)为该规则的规则强度。可选地,基于可信度的不确定性推理模型在推理分析中使用的算法包括下述的一种或多种:第一、条件合取算法,如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e分成子证据e1,e2,…,en,设e=e1ande2…anden则cf(e/e)=min{cf(e1/e1),cf(e2/e2),…,cf(en/en)};第二、条件析取算法如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e分成子证据e1,e2,…,en,设e=e1ore2…oren则cf(e/e)=max{cf(e1/e1),cf(e2/e2),…,cf(en/en)};第三、条件求补算法cf的定义可知:即表示一个前提对某个假设有利,必然对该假设的不成立不利;第四、传递算法结论h的可信度由下式给出:cf(h/e)=cf(h/e)×max{cf(e/e),0};结果h的可信度cf(h)与cf(h/e)相同,即:cf(h)=cf(h/e);第五、结果组合算法对于两个独立证据e1和证据e2分别求出的结果h的可信度cf1(h),cf2(h),用下式计算组合结果的可信度cf(h);本发明的基于可信度的湿法冶金浓密机的故障诊断方法,可以预先建立专家或操作人员的诊断经验对应的规则库,进而采用该规则库中的规则及基于可信度的不确定性推理模型进行推理分析,确定发生故障的概率,可使操作人员及时调整,有效降低事故发生率,提高生产安全性。附图说明图1为当前湿法冶金浓密过程生产流程图;图2a为本发明的故障诊断方法的流程示意图;图2b为本发明的方法中进行故障诊断的示意图;图2c为本发明中提及的不确定性推理模型的示意图;图3为本发明的离线单样本单故障识别图;图4为本发明的离线单样本多故障识别图;图5为本发明的多样本故障识别诊断图;图6为本发明的冒槽故障原因诊断图;图7为本发明的浓度偏高故障原因分布图。具体实施方式为了更好的解释本发明,以便于理解,下面结合附图,通过具体实施方式,对本发明作详细描述。本发明实施例涉及到的装置包括湿法冶金浓密机智能故障诊断系统、上位机、plc、现场传感变送部分。其中现场传感变送部分包括浓度、压力、流量等检测仪表。在湿法冶金过程现场安装检测仪表,检测仪表将采集的信号通过profibus-dp总线送到plc,plc通过以太网定时将采集信号传送到上位机,上位机把接收的数据传到湿法冶金浓密机智能故障诊断系统,进行过程工况识别并对故障进行诊断,提供生产操作指导建议。上述装置的各部分功能:①现场传感变送部分:包括浓度、压力、电流等检测仪表由传感器组成,负责过程数据的采集与传送。压力是通过siemens公司生产的dsiii型压力检测仪进行压力在线检测的,介质压力直接作用于敏感膜片上,分布于敏感膜片上的电阻组成的惠斯通电桥,利用压阻效应实现压力向电信号的转换,通过电子线路将敏感元件产生的毫伏信号放大为工业标准电流信号。液位是通过siemens公司生产的xps-15超声波液位进行液位的监测的,发射超声换能器发射出的超声脉冲,通过传播媒质传播到被测介质,经反射后再通过传声媒质返回到接收换能器,测出超声脉冲从发射到接收在传声媒质中传播的时间。再根据传声媒质中的声速,就可以算得从换能器到介质面的距离,从而确定液位。②plc:负责把采集的信号a/d转换,并通过以太网把信号传送给上位机。plc控制器采用simens400系列的cpu414-2,具有profibusdp口连接分布式io。为plc配备以太网通讯模块,用于上位机访问plc数据。plc控制器和以太网通讯模块放置在中央控制室中的plc柜中。③上位机:收集本地plc数据,传送给湿法冶金浓密机智能故障诊断系统,进行过程状态识别并对故障进行诊断,并提供生产操作指导建议。如图2a所示,本实施例的基于可信度的湿法冶金浓密机的故障诊断方法包括下述步骤:201、获取湿法冶金浓密机的在线变量。举例来说,湿法冶金浓密机的在线变量可包括:直接测量的反映浓密机生产状态的变量,以及通过直接测量的变量分析的反映浓密机生产状态的变量。其中,直接测量的变量包括:矿浆压力一、矿浆压力二、中心搅拌电机电流、压滤机前缓冲槽液位和/或渣浆泵电流等;通过直接测量的变量分析的反映浓密机生产状态的变量包括:压滤机前缓冲槽液位变化率、耙底压力、底流流量和/或底流浓度等。202、根据在线变量,确定每一变量的模糊维度;所述模糊维度为预先建立的专家规则库中的规则前件中所包括的变量对应的模糊维度。本实施例的模糊维度即模糊概念可理解为偏大、正常、偏小等维度或模糊概念,即专家规则中一系列的“偏大”、“偏小”等维度或概念。例如专家规则库中的变量包括:耙底压力、中心搅拌电机电流等,变量的模糊维度/模糊概念可为耙底压力大、中心搅拌电机电流过大等。在专家规则库中每一规则的规则前件均包括变量的模糊维度,为此,可根据专家规则库中的规则前件涉及的变量的模糊维度,计算该维度下的可信度。由此,可以减少后续可信度确定过程中的计算机处理量,提高处理效率。在其他实施例中,可不用确定模糊维度,可直接采用模糊隶属度函数获取该变量的可信度,这里的可信度包括模糊维度的可信度,还可包括不属于模糊维度的可信度等。本实施例为更好的减少后续计算机处理的处理量,提高处理效率,在磁确定模糊维度。203、针对每一个变量及该变量的模糊维度,采用模糊隶属度函数获取该变量所属模糊维度的可信度。举例来说,在本实施例中,可根据下述公式,获取每一变量的可信度;其中,k为经验系数,xmean为预先设定的待分析的变量的正常范围平均值,x为待分析的变量,μcf(x)为待分析的变量的可信度。若前述步骤202中确定有模糊维度,则可采用上述公式计算属于模糊维度的可信度即可,进而减少计算量,提高处理效率。可信度可理解为变量模糊维度的量化,是一个在[0,1]之间的小数。204、基于可信度的不确定性推理模型结合专家规则库中的规则,对每一变量的可信度进行推理分析,得到故障结论可信度。举例来说,预先建立的专家规则库中,每一浓密机故障诊断专家规则包括:通过变量的模糊维度表达的规则前件、通过结论表达的规则后件、说明结论可信度的规则强度;每一个规则的规则前件、规则后件和规则强度具有对应关系;所述规则前件中的变量具有至少一个模糊维度。另外,应说明的是,基于可信度的不确定性推理模型中,产生式规则的形式为:ifethenhwithcf(h/e)其中,e表示一个简单前提,或多个简单前提逻辑组合的逻辑组合前提,h为一个或多个结论,cf(h/e)为基于所述e发生h的可信度;相应地,采用产生式规则的形式表示专家规则库的中规则前件、规则后件、规则强度的对应关系,则理解为为:e表示每一规则的规则前件中的变量的模糊维度,h为该规则的规则后件中的结论,cf(h/e)为该规则的规则强度。另外,举例来说,假设专家判断浓度正常与否是通过变量x1进行的,对流量正常与否是通过变量x2进行的。专家规则库中的每条模糊规则的形式上都如下面的规则一和规则二:规则一:if浓度偏大and流量偏小,then(假设a发生)cf(h/e)=0.8规则二:if浓度偏小or流量偏小,then(假设b发生)cf(h/e)=0.9其中,浓度偏大、浓度偏小、流量偏小都是模糊维度。μcf(浓度偏小)(x1)、μcf(浓度偏大)(x1)μcf(流量偏小)(x2)三个模糊维度的可信度分别通过存储在规则库中的根据经验定义好的模糊隶属度函数求得。由于规则一中前提“浓度偏大and流量偏小”是由两个子前提的逻辑与,因此需要用可信度的逻辑与公式计算总的前提e(也就是浓度偏大and流量偏小)成立的可信度,然后通过传递算法,结合cf(h/e)=0.8求得结论(假设a发生)的可信度。205、将故障结论可信度与预设阈值进行比较,根据比较结果确定是否发生故障及发生故障的概率。具体地,若故障结论可信度大于预设阈值,则确定发生故障,且将故障结论可信度作为发生故障的概率,以及根据故障结论可信度确定故障发生可能的原因;若故障结论可信度小于等于预设阈值(阈值τ可设为0.6),则确定不发生故障,结束。本实施例的方法可以预先建立专家或操作人员的诊断经验对应的规则库,进而采用该规则库中的规则及基于可信度的不确定性推理模型对当前的在线变量进行故障诊断,可使操作人员根据故障诊断结果及时调整,进而有效降低事故发生率,提高生产安全性。也就是说,利用可测过程变量在线识别生产过程的运行状态;为实际生产操作及管理人员实时提供浓密机生产运行状态信息,确保企业生产效率和经济效益;在生产过程出现异常和故障时,自动追溯其原因,为操作工提供合理可靠的操作指导建议;提供实时的过程诊断和原因追溯结果,避免人工评价的滞后问题,并及时对当前生产周期过程运行状态做出适当调整。在一种可选的实现方式中,上述的步骤201之前,图2a所示的方法还可包括预先建立专家规则库的步骤。在具体应用中,预先建立专家规则库可具体为下述的步骤200a至200c:200a、离线获取预设时间段内湿法冶金浓密机的历史变量;200b、结合湿法冶金领域专家及相关操作人员的先验知识、获取多个浓密机故障诊断专家规则;200c、根据浓密机故障诊断专家规则,建立专家规则库,如下表3所示的专家规则库中的规则。其中,每一浓密机故障诊断专家规则包括:通过变量的模糊维度表达的规则前件、通过结论表达的规则后件、说明结论可信度的规则强度;每一个规则的规则前件、规则后件和规则强度具有对应关系;所述规则前件中的变量具有至少一个模糊维度。在一种可选的实现方式中,前述步骤204之前,所述方法还包括下述的图中未示出的步骤:204a、判断在线变量中多个变量是否反映同一个证据,如果是,则将反映同一个证据的多个变量的可信度进行逻辑组合;否则,执行步骤204.其中,证据为与专家规则库中的每一规则前件对应,且属于在线变量反映的规则前件;相应地,步骤204可具体为:基于可信度的不确定性推理模型结合专家规则库的规则对逻辑组合的多变量的可信度进行推理分析。在实际应用中,204a中的判断在线变量中多个变量是否反映同一个证据的步骤可具体为:查找在线变量中每一变量所匹配的规则对应在专家规则库中的规则标识;相应地,将反映同一个证据的多个变量的可信度进行逻辑组合的步骤可具体为:将属于同一规则标识的多个变量的可信度按照该规则标识中各个变量的逻辑组合关系进行逻辑组合。例如下述表3中,规则11中,浓度低于设定阈值且5小时前底流流量正常;其中,低于设定阈值、5小时前底流流量正常是逻辑与的关系;进而针对在线变量中的浓度的可信度与底流流量的可信度需要进行逻辑与组合。为更好的理解本发明实施例中的不确定性模型,以下结合图2c进行简单说明。该不确定性模型中表示不确定性时使用的符号是c(x),区别于将可信度引入到该模型中以后,不确定性的表示符号变化为cf(x),两者的关系是“一般到特殊”的关系。不确定性模型定义了模型中的各种概念、描述了这些概念所带有的不确定的程度以及不确定性的传递过程。在不确定性模型中,产生式规则通过if-then描述了事件“如果前提e描述的事件发生,则假设h发生”的因果关系,还通过计算因果的可信度来描述事件h最终发生的可信程度是多少。该泛化的模型中,图2c中虚线上面的部分是描述规则库中规则所包含的不确定性。规则库中是很多由前提e推理得到假设h的规则。c(h/e)描述由前提推理假设成立的可信程度。这部分内容是离线建立专家规则库时,由专家给出的信息。(这就是专家规则存在的必要性。e和h的因果关系由规则给出,而其可信程度由规则强度,也就是规则的可信度量化给出)而图2c中虚线下部分表示该模型在推理过程中,不确定性的计算和传递过程。这部分是在线推理过程。e为规则中的前提,h为规则中的假设。e为观察到的证据,h为对应h的结论,一般情况下,可以认为h和h描述的是同一件事。只是为了在该模型中类似e和e的对应关系,而存在的对应而已。对于规则库中的规则,前提e和假设h是一组对应概念,是由专家给定的。在实际应用时,e是对规则中前提描述的e的观察,不一定完全符合,有一定的匹配度,下述均称为证据。在证据中,分为初始证据和中间证据。在可信度的不确定模型中,初始证据的可信度是通过“数据---模糊隶属度函数”计算得到的模糊概念的可信度;而中间证据的可信度是有些之前推理得到的结论被重新继续用于推理,也就是说中间证据不需要经过“数据——模糊隶属度函数”来计算可信度。不确定性的传递过程就是由证据的不确定性结合规则的不确定性推理得到结论不确定性的过程,因果关系由规则确定好了,不确定性的定量计算由下述的推理分析中使用的下述的几个算法,如cf(h/e)=cf(h/e)×max{cf(e/e),0}得到当前证据e下,假设h的可信度。进一步地,前述的步骤204中的基于可信度的不确定性推理模型在推理分析中使用的算法了包括下述的一种或多种:第一、条件合取算法,如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e分成子证据e1,e2,…,en,设e=e1ande2…anden则cf(e/e)=min{cf(e1/e1),cf(e2/e2),…,cf(en/en)};第二、条件析取算法如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e分成子证据e1,e2,…,en,设e=e1ore2…oren则cf(e/e)=max{cf(e1/e1),cf(e2/e2),…,cf(en/en)};第三、条件求补算法cf的定义可知:即表示一个前提对某个假设有利,必然对该假设的不成立不利;第四、传递算法结论h的可信度由下式给出:cf(h/e)=cf(h/e)×max{cf(e/e),0};结果h的可信度cf(h)与cf(h/e)相同,即:cf(h)=cf(h/e);第五、结果组合算法对于两个独立证据e1和证据e2分别求出的结果h的可信度cf1(h),cf2(h),用下式计算组合结果的可信度cf(h);另外,需要说明的是,前提e和假设h是一组对应概念,是由专家规则库中预先给定的。在实际应用时,e是对规则中前提描述的e的观察,不一定完全符合,有一定的匹配度,称为证据。而证据中,又分为初始证据和中间证据,初始证据的可信度是通过“数据---模糊隶属度函数”计算得到的模糊概念的可信度;而中间证据的可信度是有些之前推理得到的结论被继续用于后序步骤的推理,也就是说中间证据不需要经过“数据——模糊隶属度函数”来计算可信度。另外,如图2b所示,本实施例的方法可具体说明如下。第一步、离线阶段,在预设时间段内湿法冶金浓密机的历史数据中选择可用的故障诊断变量。可理解的是,选择可用的故障诊断变量主要是深入分析浓密机运行机理,分析主要的异常和故障。从众多变量中找出能充分体现浓密机运行状态的变量,以此为基础,进行异常和故障规则的提取。本实施例中以某湿法冶金企业浓密流程作为研究对象。生产流程如图1所示,上一级的矿浆由进料管道输送到浓密机中,在浓密机中经过重力沉降得到的高浓度矿浆通过底流管道运输到浓密机下缓冲槽中,之后由渣浆泵抽出送至压滤机前缓冲槽中,以备压滤机进行压滤环节。其中,能反映浓密机生产状态的直接测量变量有五个,分别是:矿浆压力1、矿浆压力2、中心搅拌电机电流、压滤机前缓冲槽液位、渣浆泵电流,如表1所示。表2是一些不可直接测量但可以通过可测变量进一步分析得到的变量。表1浓密过程可测变量表可测变量符号单位矿浆压力1、2p1兆帕中心搅拌电机电流i1安培压滤机前缓冲槽液位l米渣浆泵电流i2安培表2浓密过程可近似反映的变量表第二步、根据上述的故障诊断变量建立浓密机故障诊断专家规则库,并为每一条规则赋予规则强度。该步骤中建立了浓密机故障诊断专家规则库:根据过程知识和专家经验,总结专家对过程进行工况识别和故障诊断时的经验,将多条规则汇总为故障诊断专家规则库。这些规则都有不确定程度,以规则强度来表达规则的可信程度。具体地,本实施例中根据领域专家和现场操作人员的经验、知识,总结出浓密过程故障诊断专家规则,如表3所示。其中,规则1、2为压耙故障,3、4、5、6为冒槽故障,这两类故障对生产的影响较大,一旦发生必须停机检查,影响生产进行;规则7、8为底流流量故障;规则9、10、11为底流浓度故障。浓密机相关经验规则较多,此处仅列举部分仿真实验可能用的规则用来诊断以下这些故障。表3浓密过程故障诊断专家规则表通常,根据专家经验总结的专家规则也可以理解为基于可信度的浓密机故障诊断的离线建模过程。规则强度如表3右侧栏的记载,规则强度的给出可以根据历史数据的统计得到,也可以由工艺专家和操作人员根据操作经验给出。第三步、获取湿法冶金浓密机在预设周期内的在线变量。预设周期可为预先定义的如一小时、半小时等。这里的在线变量可以是测量的数值,也可以不是测量的数值,采用其他方式如划分等级方式描述的变量等。第四步、根据在线变量,确定每一变量的模糊维度;针对每一个变量及该变量的模糊维度,采用模糊隶属度函数获取该变量所属模糊维度的可信度。需要说明的是,在实际应用中,专家规则库中规则涉及的维度可能仅是偏大一个方面,故确定偏大的模糊维度之后,可获取可信度时仅获取偏大维度的可信度即可,减少计算偏小维度或正常维度的可信度的过程,进而减少计算复杂度。模糊隶属度函数公式如下:其中,xmean为变量的正常范围平均值;k为系数,一般在0.25-1.5之间。需要说明的是,通常,对于初始证据的可信度由操作人员在智能故障诊断系统运行时提供;中间证据,由前提推出的结果作为当前推理的证据,最终结论的可信度由下述基于可信度的不确定推理模型求出。一般地,初始证据可信度赋值方法是根据经验赋值,得到的结果主观性强。为了消除初始证据可信度赋值偏主观的弊端,本实施例采用模糊隶属度函数获取初始证据的可信度。根据经验,通过引入模糊隶属度函数,将在线变量的可信度数值求出来。使用模糊隶属度函数的初始证据可信度赋值的方法对规则前件中的各个模糊维度赋初始可信度。偏大和偏小的概念都是针对均值而言的,表4是各个变量的正常范围平均值:表4变量的正常范围平均值变量正常范围平均值阈值中心搅拌电机电流12a/耙底压力0.06kpa/压滤机前缓冲槽液位/450cm底流浓度45%48%渣浆泵电流28a20a压滤机前缓冲槽液位变化率4cm/min/由模糊隶属度函数只能求出单一证据的可信度。当多变量反映同一证据时,需要通过不确定性推理模型中的至少一个算法计算最终证据的可信度。第五步、基于可信度的不确定性推理模型结合专家规则库中的规则,对每一变量的可信度进行推理分析,得到故障结论可信度。在基于可信度的不确定性推理模型中,知识(即专家经验总结的内容)是以产生式规则的形式表示的。可信度方法实际是一种部分模糊化的规则系统,即设置规则可信度的方法。知识的不确定性则是以可信度cf(h/e)表示。产生式规则的一般形式如下:ifethenhwithcf(h/e)其中,e为前提,它既可以是一个简单前提,也可以是由多个简单前提构成的逻辑组合;h是假设,它可以是一个或多个结论;cf(h/e)是基于所述e发生h的可信度,它表示当前提e为真时,假设h有cf(h/e)大小的可信度。证据的不确定性用证据的可信度cf(e)表示。证据的不确定性问题反映了证据被肯定的程度,当证据肯定为真时,则取cf(e)=1;当证据肯定为假时,则取cf(e)=-1;当对证据一无所知时,则取cf(e)=0。针对基于可信度的不确定性推理模型中的不确定性推理计算不确定性的推理计算是指从不确定的初始证据出发,通过运用相关的不确定性知识,最终推出结论并求出结论的可信度。它所运用的算法有:(1)条件合取算法如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e也就可分成相应子证据e1,e2,…,en,设e=e1ande2…anden则cf(e/e)=min{cf(e1/e1),cf(e2/e2),…,cf(en/en)};(2)条件析取算法如果前提e是n个子前提e1,e2,…,en的逻辑组合,那么证据e也就可分成相应子证据e1,e2,…,en,设e=e1ore2…oren则cf(e/e)=max{cf(e1/e1),cf(e2/e2),…,cf(en/en)};(3)条件求补算法由cf的定义可知:也就是说它表明一个证据对某个假设有利,必然对该假设的不成立不利,而且对两者的影响程度相同。(4)传递算法结论h的可信度由下式给出:cf(h/e)=cf(h/e)×max{cf(e/e),0};cf方法认为结果的可信度cf(h)与cf(h/e)相同,即:cf(h)=cf(h/e)(5)结果组合算法在cf方法中,也称新证据法则。对于两个独立证据e1和e2分别求出的结果h的可信度cf1(h),cf2(h),用下式计算组合结果的可信度cf(h)。本实施例中的不确定性推理计算:在线应用时,采集到的数据与相关规则前件会存在匹配程度,根据基于可信度的不确定性推理模型自身的不确定性推理规则,对过程进行不确定性推理,最终得到含有不确定性的过程运行状态识别结论或者故障诊断结论。在线实时故障诊断时,遍历规则库中的所有规则,推理得到相关规则的结论和可信度,当可信度大于设定的阈值时,才认可该结论描述的异常发生,否则认为没有发生。也就是说,当结论的可信度小于阈值时,认为该规则规定的故障没有发生,诊断过程结束。当结论的可信度大于阈值时,说明规则后件成立,即可得出故障的原因及其可信度。也就是说,判断是否产生式规则前件中的所有证据都满足。当前件中的证据不是都满足时,停止推理,该规则规定的故障没有发生。当前件中的所有证据都满足时,结合产生式规则的规则强度,计算规则后件的可信度。以下仿真所使用数据均为某精炼厂实际运行数据,所采集的样本中有压滤机前缓冲槽冒槽、渣浆泵进气、底流管道堵塞、底流浓度异常等多种故障。选取发生底流管道堵塞故障的样本进行单故障识别的仿真验证,结果如图3所示。经基于可信度的不确定性推理模型进行推理计算后,只有底流管道堵塞(规则7)的规则前件被满足,且其可信度为0.713,大于阈值0.6。故障识别结果为只有底流管道堵塞一个故障发生,诊断结果与实际现场故障相符。上述方法也可对多故障共发的情况进行识别。选取底流管道堵塞和浓度偏大两个故障同时发生的样本进行仿真验证,仿真结果如图4所示。底流管道堵塞(规则7)和浓度偏大(规则9)的规则前件同时被满足,且其可信度分别为0.66和0.633,均大于阈值0.6。故诊断结果为底流管道堵塞和浓度偏大同时发生,故障识别结果与现场实际故障相符。很多情况下,有些故障是并发的,为了验证该方法在多故障并发时的工况识别的有效性,选取500组样本进行故障诊断仿真验证。其中0-50及401-500为正常;51-150为渣浆泵进气(规则8);151-250为底流管道堵塞(规则7);251-300为进料量偏大导致浓度偏大(规则10);300-350为底流流量偏小导致浓度偏大(规则9);350-400为浓度高流量大导致压滤机前缓冲槽冒槽(规则6),仿真结果如图5所示。其中多个采样点出现故障并发的情况。异常识别结果直观的呈现采样样本的故障类型。故障诊断需要了解导致每种故障的可能原因,即故障原因追溯。由于压滤机前缓冲槽冒槽故障一旦发生,必须停机检查,确保生产安全,故将其归为严重故障。以此为仿真对象进行研究,在对冒槽故障进行原因追溯检测时,选取500组样本进行仿真验证。其中,0-425为正常状态,426-450为浓度高流量大导致冒槽,450-475为流量大导致冒槽,476-500恢复正常状态,如图6所示。原因诊断结果与实际一致,只有个别样本诊断错误。在故障原因追溯时,可以直观的反应出了各个异常与阈值的相对关系,更加直观。底流流量小和进料量大是导致浓度偏高的两个主要原因。在使用上述方法的基于可信度的不确定性推理模型推理用于故障原因诊断的仿真中。分别使用现场工人给出的证据可信度和通过模糊隶属度得到的证据可信度进行仿真。实验选取500组样本,其中,底流流量小导致浓度偏大这一故障占200组,如图7所示。使用误判率和漏判率对两种仿真进行对比,如表5所示:表5初始证据赋值方法的对比使用隶属函数根据经验赋值误判率3.8%9.4%漏判率8.5%22.5%可以看出,使用隶属函数对初始证据赋值的误判率和漏判率明显小于根据经验的赋值。以上结合具体实施例描述了本发明的技术原理,这些描述只是为了解释本发明的原理,不能以任何方式解释为对本发明保护范围的限制。基于此处解释,本领域的技术人员不需要付出创造性的劳动即可联想到本发明的其它具体实施方式,这些方式都将落入本发明的保护范围之内。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1