基于二维最佳直方图熵法与遗传算法的离焦躁声消除方法与流程

本发明属于光学扫描全息领域，涉及一种基于二维最佳直方图熵法与遗传算法的离焦躁声消除方法。

背景技术：

光学扫描全息技术(opticalscanningholography)，简称osh，是数字全息技术的一个分支，它是由poon和korpel最早提出，osh可以将三维物体的信息存储为二维的全息图。自该项技术提出以来，已在扫描全息显微镜、3d图像识别以及3d光学遥感等领域得到广泛应用。在osh中，从全息图重建出各层的切片图像时，传统的重建方法会使得到的重建图像含有其他层切片的离焦躁声，导致成像质量差；为此，离焦躁声的消除成为我们研究的重点。

目前，文献《thresholdingusingtwo-dimensionalhistogramandfuzzyentropyprinciple》中公开一种利用二维直方图阈值和模糊熵来处理带噪图像，但是二维直方图熵法设计参数多，运行速度较慢，效果不是很理想。文献《imagedenoisingbasedongeneticalgorithm》中公开一种利用遗传算法进行图像去噪，但是该传统遗传方法搜索效率较慢，不能快速找到全局最优解，即不能高效的进行图像去噪处理。

技术实现要素：

本发明的目的在于针对上述问题，提供了一种基于二维最佳直方图熵法与遗传算法的osh中离焦躁声消除方法，通过提取图像灰度信息，利用二维最佳直方图熵法选取阈值，并利用改进型遗传算法加快收敛速度，提高阈值搜索效率，从而得到最佳阈值进行图像分割，有效提高切片成像质量。

为实现上述目的，本发明采用的技术方案为：

基于二维最佳直方图熵法与遗传算法的离焦躁声消除方法，包括以下步骤：

步骤1.将激光通过第一个偏振分束器分为两束光路，其中，第一光瞳为随机相位光瞳p1(x,y)＝expj[2πr(x,y)]、r(x,y)为(0,1)之间的随机函数，第二光瞳为p2(x,y)＝1，其中，x,y分别代表空间坐标信息；将分别经过两束光路的两条光束由第二个偏振分束器聚光后干涉形成菲涅尔干涉条纹；

步骤2.利用菲涅尔干涉条纹对待测物体进行二维扫描，并通过光电检测器接收扫描后的光信息，从而获得待测物体的全息图；

步骤3.将所得全息图做傅里叶变换后，与带有距离参数的随机相位光学传递函数的频域表达式的共轭相乘后，再经过逆傅里叶变换，则得到待测物体的重建灰度图，其中包含呈散斑噪声形式的离焦噪声；

步骤4.将重建得到的灰度图采用二维最佳直方图熵法，设定门限阈值向量(s,t)，得到二维直方图的总熵为h(s,t)：

其中，pa表示背景概率，pb表示目标概率，ha表示目标区域的熵，h表示整个图像的熵；

以h(s,t)为适应度函数，采用遗传算法搜索最优阈值。

进一步的，所述步骤1中通过分别设置两个光瞳，则光学传递函数表示为：

其中，k0代表波数，kx和ky代表空间频率，f是透镜焦距，p1是第一光瞳为随机相位光瞳p1(x,y)的傅里叶变换，zi,i＝1,2,3,...,n表示第i层物体到扫描平面的距离，n为总层数。

更进一步的，所述步骤2中得待测物体的全息图表示为：

其中，g(x,y)表示全息图，f^-1、f分别表示傅里叶逆变换和傅里叶变换，i(x,y；zi)表示待测物第i层的复振幅函数。

所述步骤3的具体过程为：

选择p1d和p2d作为解码光瞳，其中，p1d(x,y)＝1、用于重建第i层图形，则，通过光学传递函数重建图像的具体表达如下：

其中，i′(x,y；zi)表示待测物体第i层的重建图像信息，n(x,y；zi)表示散斑噪声；则：

所述步骤4中遗传算法的具体过程为：

(1)随机生成初始化种群；

(2)选择初始种群规模为popsize,最大进化代数gmax；

(3)适应度函数：以h(s,t)作为适应度函数；

(4)编码：采用八位灰度图像进行编码，门限参数设为0≤s,t≤255，将个体编码为16位二进制码，高八位代表s，低八位代表t；解码也同样将高八位解码为s，低八位解码为t；

(5)选择算子：采用精英策略和轮盘赌法相结合，根据精英策略将群体中10％的优秀个体直接复制到下一代，然后对剩下的个体运用轮盘赌法进行选择；

(6)交叉算子：设定搜索前期的交叉概率pc＝0.85,搜索后期的交叉概率为pc＝0.65；

(7)变异算子：选择抛物线型算子pm，定义如下：

其中，pmmax＝20pmmin，pmmin＝pb、pb为基本变异概率，g∈(1,gmax)；

(8)终止算法：当达到最大进化代数时终止算法，即得到最优阈值。

本发明的有益效果在于：

(1)本发明通过设置光瞳，将离焦噪声变为散斑噪声形式，然后将二维最佳直方图熵法与遗传算法相结合去除osh中离焦噪声的方法，二维最佳熵法充分利用了像素的灰度分布信息和像素间的空间相关信息,提高了阈值分割的抗噪性能；

(2)本发明利用改进的遗传算法加快了搜索过程的收敛性，最终得到了全局最优解；遗传算法应用范围包括机器人学、图像处理、自动控制等，因此本发明适用于很多领域，应用范围非常广；

(3)本发明不仅实现方式简单、便于操作，同时具有很强的实用性，适合推广使用。

附图说明

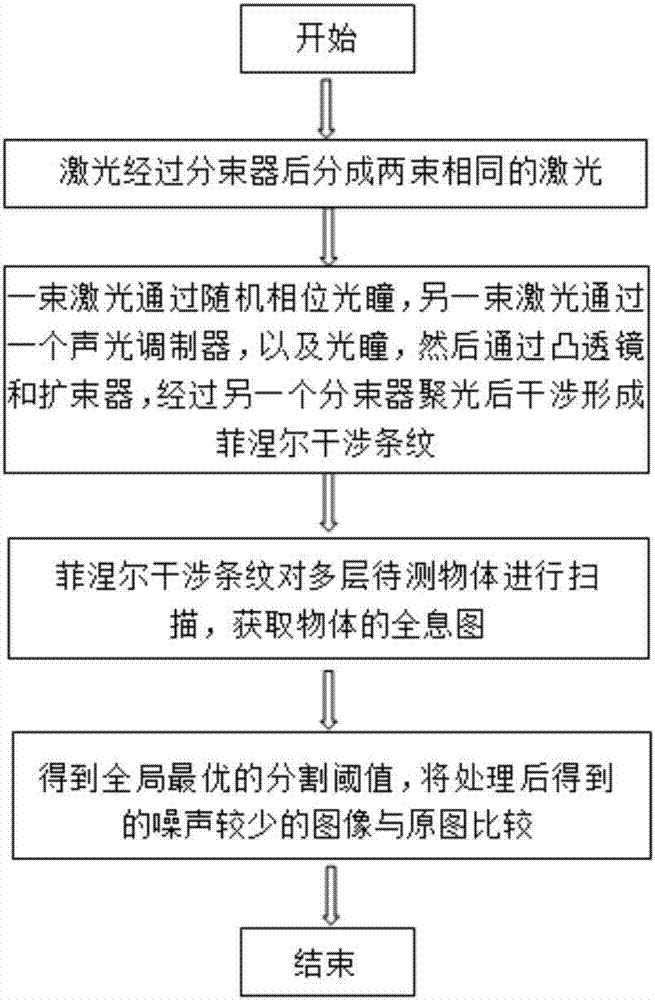
图1为本发明提供基于二维最佳直方图熵法与遗传算法的离焦躁声消除方法的流程示意图。

图2为实施例中采用的osh系统基本结构图。

图3为实施例中采用原图。

图4为实施例中在随机相位函数编码的osh系统中重建图像。

图5为实施例中对重建图像进行离焦躁声消除后得到结果。

图6为实施例步骤4中二维直方图。

具体实施方式

下面结合实施例和附图对本发明进行详细说明。

本实施例提供一种基于二维最佳直方图熵法与遗传算法的离焦躁声消除方法，其流程示意图如图1所示，本实施例中，系统结构如图2所示，其原图如图3所示，具体实施过程包括以下步骤：

步骤1.采用如图2所示的系统结构图，由同一激光源发出的角频率为ω的光通过第一个偏振分束器分为两束光路，其中第一光瞳为随机相位光瞳p1(x,y)＝expj[2πr(x,y)],r(x,y)为(0,1)之间的随机函数，由透射型空间光调制器(spatiallightmodulator,slm)实现；而第二光瞳为p2(x,y)＝1，其中，x,y分别代表空间坐标信息；将这两条光束经过第二个偏振分束器聚光后干涉形成菲涅尔干涉条纹；则，光学传递函数表示为：

其中，k0代表波数，kx和ky代表空间频率，f是透镜焦距，p1是第一光瞳为随机相位光瞳p1(x,y)的傅里叶变换，zi,i＝1,2,3,...,n表示第i层物体到扫描平面的距离，n为总层数；

步骤2.通过上述的菲涅尔干涉条纹对待测物体进行扫描，并利用光电检测器接收扫描后的光信息，从而获得待测物体的全息图：

其中，g(x,y)表示全息图，f^-1、f分别表示傅里叶逆变换和傅里叶变换，i(x,y；zi)表示待测物第i层的复振幅函数；

步骤3.将所得的全息图做傅里叶变换后，与带有距离参数的随机相位光学传递函数的频域表式的共轭相乘后，再经过逆傅里叶变换，即可得到待测物体的重建图像；通过对光瞳的设计，我们可以将传统切片成像中的离焦噪声表示为散斑噪声的形式，如图4所示；

本实例中，为了重建第i层的切片，我们选择p1d和p2d作为解码光瞳，其中，p1d(x,y)＝1、因此，步骤3所述的通过光学传递函数重建图像的具体表达如下：

其中，i′(x,y；zi)表示待测物体第i层的重建图像信息，n(x,y；zi)表示散斑噪声；则：

表示待测物体第i层重建图形中由第j层图形带来的噪声；

步骤4.将重建得到的灰度图用二维最佳直方图熵法在二维灰度空间搜索最佳决策变量确定最大熵值；在二维最佳直方图熵法中，设定一个门限阈值向量(s,t)，设选定灰度图的灰度值范围为(0,l-1)，将二维直方图分为如图6所示的四个区域，blocka和blockb分别代表背景和目标，blockc和blockd为边缘噪声区域，则有：

背景概率:

目标概率:

由整个图像熵的计算公式：

对于blocka和blockb两个区域，有：

对于blockc和blockd的边缘噪声区域，取值远远小于二维直方图对角线上目标和背景的取值，因此可以作合理近似忽略，则blocka和blockb概率分布有关的熵分别为：

此时二维直方图的总熵为：

根据最大熵原理，有最佳阈值：(sopt,topt)＝arg{maxh(s,t)}

其中，arg{}表示求反函数；

步骤5.用改进遗传算法来提高阈值搜索效率，最终找到最优的阈值，最后得到处理效果较好噪声较少的图像；

针对二维最佳直方图熵法的特点，对传统遗传算法作出了改进，特别是对选择、交叉、变异等算子进行了优化设置，具体改进情况如下:

(1)随机生成初始化种群；

(2)选择初始种群规模为popsize＝50,最大进化代数gmax＝100；

(3)适应度函数：以作为适应度函数；

(4)编码：采用八位灰度图像进行仿真实验，门限参数设为0≤s,t≤255,将个体编码为16位二进制码，高八位代表s，低八位代表t；解码也同样将高八位解码为s，低八位解码为t；

(5)选择算子：采用精英策略和轮盘赌法相结合，根据精英策略将群体中10％的优秀个体直接复制到下一代，然后对剩下的个体运用轮盘赌法进行选择；

(6)交叉算子：将传统遗传算法前后一致的交叉概率进行改进，搜索前期的交叉概率pc＝0.85,搜索后期的交叉概率为pc＝0.65,前期(0≤g≤50)交叉概率高使个体更新较快,能达到更大解空间,并能降低取得非最优解的概率,后期(50≤g≤100)降低交叉概率,加快收敛速度，尽快得到全局最优解；

(7)变异算子：选择抛物线型算子pm，定义如下：

上式中，pmmax＝20pmmin,pmmin＝pb,g∈(1,gmax),在进化前期、中期以及后期以不同概率变异已达到最优的效果，在进化前期，以较小概率变异，维持一个良好的进化模式；进化中期以加大变异概率，提高搜索能力，避免陷入局部最优；进化后期，减小变异概率，加快算法收敛到全局最优解的速度；pb为基本变异概率，可按下式进行估计：

当pb≈0.009,gmax＝100时，可得变异算子pm为：

pm＝pm(g)＝0.09-0.0000684×(g-50)²；

(8)终止算法：当达到最大进化代数时终止算法，

当遗传算法最后满足终止条件时，将具有最高适应度的个体作为遗传算法的全局最优解，即maxh(s,t),由(sopt,topt)＝arg{maxh(s,t)}可得对重建图像进行分割的最佳阈值，得到去噪后重建图像如图5所示。

以上所述，仅为本发明的具体实施方式，本说明书中所公开的任一特征，除非特别叙述，均可被其他等效或具有类似目的的替代特征加以替换；所公开的所有特征、或所有方法或过程中的步骤，除了互相排斥的特征和/或步骤以外，均可以任何方式组合。