用于超光谱成像平台中双相机图像的对齐方法与流程

本发明涉及超光谱成像平台中双相机图像的对齐方法，具体涉及超光谱成像的图像融合平台中低分辨率超光谱相机和高分辨率rgb相机拍摄的两张图像的对齐方法，属于计算摄像学领域。

背景技术：

超光谱成像是一项具有重要意义的技术，它可以提高目标分割、目标追踪、目标识别等算法的性能，在遥感方面的应用使其对地质、海洋、大气和环境领域的研究有重要推动作用。近年来，该项技术也越来越多地应用于商业市场，例如生物技术、生命科学及医学领域。

传统的超光谱成像技术通常利用分光器件如光栅、棱镜等，通过多次成像的方式获取平面场景的超光谱图像。这些技术存在一些缺点，例如设备造价昂贵、成像过程耗时较长、每次曝光要求场景不变等。

随着稀疏表达技术的发展，出现了基于单次曝光的超光谱成像技术。其中，图像融合平台自从出现以来，被国内外研究者不断改进，达到了较好的成像效果。这种平台使用两台相机拍摄完全相同的场景，一台相机为低分辨率超光谱相机，另一台为高分辨率rgb相机。在得到两台相机拍摄的图像后，使用基于稀疏表达的算法，对两张图像进行融合而得到高分辨率超光谱图像。

图像融合平台较好地解决了传统超光谱成像技术需要多次曝光的缺点，但是仍存在一些不足。其中最明显的不足是双相机对齐问题，即该平台要求两台相机拍摄完全相同的场景。图像融合平台通常使用一种半反半透镜(beamsplitter)来解决这一问题，这种元件可以将完全相同的场景投射到不同的成像设备。然后，通过使用标定板等装置，对相机位置进行调整，尽可能达到双相机对齐的效果。

对于两台高分辨率相机，传统的对齐方法能够达到不错的效果。但是，由于图像融合平台采用低分辨率超光谱相机，得到的图像相对高分辨率图像常常有8倍到32倍的模糊，这样的模糊程度使得人眼识别标定点的过程更加困难。另外，传统的软件对齐算法，也要求两张图像有较高重合程度，而图像融合平台拍摄的两张图像显然不能满足这种要求。因此，图像融合平台对于一种针对分辨率不同的两张图像的对齐算法，具有十分急切的需求。

技术实现要素：

针对现有技术不具备对高分辨率rgb图像和低分辨率超光谱图像的对齐方法的问题。基于超光谱成像平台中双相机图像对齐提高超光谱成像算法精度的同一发明构思，本发明公开两种用于超光谱成像平台中双相机图像对齐的方法：

第一种用于超光谱成像平台中双相机图像对齐的方法要解决的技术问题是：提供一种针对低分辨率超光谱图像和高分辨率rgb图像的对齐方法，通过图像对齐能够提高基于图像融合平台的超光谱成像算法的精度。

第二种用于超光谱成像平台中双相机图像对齐的方法要解决的技术问题是：提供一种适用于超光谱成像的图像融合平台中的高分辨率rgb图像和低分辨率超光谱图像的对齐方法，通过超光谱重建和对齐过程的迭代，能够提高图像对齐的精确度和超光谱重建的精度。

为达到以上目的，本发明采取以下技术方案：

本发明公开的第一种用于超光谱成像平台中双相机图像对齐的方法，应用于超光谱成像的图像融合平台，使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像；对rgb图像进行空间下采样得到低分辨率rgb图像，对超光谱图像进行光谱域下采样得到与空间下采样相同尺寸的低分辨率rgb图像；对所述的两张低分辨率rgb图像建立图像对齐模型；使用对齐模型求解算法求解对齐模型中的单应变换矩阵；使用所述单应变换矩阵，对所述高分辨率rgb图像进行变换，使高分辨率rgb图像与所述低分辨率超光谱图像对齐，从而提高基于图像融合平台的超光谱成像算法的精度。

本发明公开的第一种用于超光谱成像平台中双相机图像对齐的方法，包括以下步骤：

步骤101：使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像。

步骤102：对rgb图像进行空间下采样得到低分辨率rgb图像，对超光谱图像进行光谱域下采样得到与空间下采样相同尺寸的低分辨率rgb图像。

步骤103：根据图像对齐模型对步骤2所述的两张低分辨率rgb图像进行对齐处理。

步骤103所述的图像对齐模型优选公式(1)所示的图像对齐模型：

其中t表示待求单应变换，x表示二维平面上的坐标点，y表示所述高分辨率rgb图像，l表示拍摄的低分辨率超光谱图像，h表示所述低分辨率超光谱图像的空间下采样矩阵，p代表rgb相机光谱响应曲线，即光谱域下采样矩阵，||·||f表示矩阵的frobenius范数。

上述模型要求高分辨率rgb图像和低分辨率超光谱图像具有完全相同的辐射强度。但是在实际应用中，两台相机因为硬件原因，总体亮度上通常会存在差别，因此，步骤103所述的图像对齐模型优选增强相关系数模型，即如公式(2)所述的图像对齐模型：

步骤104：根据对齐模型求解方法求解步骤103所述的图像对齐模型，得到矩阵形式的单应变换。

所述的对齐模型求解方法优选lucas-kanade方法、运动估计方法、基于傅里叶变换的对齐方法等。

其中lucas-kanade方法可以通过迭代的方式求解单应变换矩阵。为了加快迭代的收敛速度，lucas-kanade组合算法和反向组合算法等变种也同样适用于本问题的求解。

步骤105：根据所述单应变换矩阵，对所述高分辨率rgb图像进行变换，使高分辨率rgb图像与所述低分辨率超光谱图像对齐。通过图像对齐能够提高基于图像融合平台的超光谱成像算法的精度。

本发明还公开第二种用于超光谱成像平台中双相机图像对齐的方法，应用于超光谱成像的图像融合平台，使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像；把单应变换矩阵初始化为单位矩阵；迭代进行以下超光谱重建和对齐的步骤，直至达到预设的迭代次数：对所述高分辨率rgb图像和低分辨率超光谱图像使用图像融合算法进行超光谱图像重建，得到重建的超光谱图像；对重建的超光谱图像进行空间下采样；对采集的低分辨率超光谱图像和空间下采样后的重建的超光谱图像，建立对齐模型；使用对齐模型求解算法，更新所述单应变换矩阵；使用更新后的单应变换矩阵对所述高分辨率rgb图像进行变换。通过上述超光谱重建和对齐的迭代步骤，能够提高图像对齐的精确度和超光谱重建的精度。

本发明还公开第二种用于超光谱成像平台中双相机图像对齐的方法，包括以下步骤：

步骤201：使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像。

步骤202：把单应变换矩阵进行初始化，设置为单位矩阵。

步骤203：对获取的高分辨率rgb图像和低分辨率超光谱图像通过图像融合算法进行超光谱图像重建，得到重建的超光谱图像。

所述的图像融合算法优选：基于稀疏矩阵分解的图像融合算法，基于空间-光谱稀疏表达的图像融合算法，基于成对图像光谱分解的图像融合算法，基于非负结构化稀疏表达的图像融合算法等。

步骤204：对重建的超光谱图像进行空间下采样，使它的空间分辨率与采集的低分辨率超光谱图像一致。

步骤205：对采集的低分辨率超光谱图像和空间下采样后的重建的超光谱图像，根据对齐模型进行对齐处理。

步骤205所述的对齐模型优选公式(3)所示对齐模型。

其中t表示待求单应变换，x表示二维平面上的坐标点，l′表示所述空间下采样后的重建的超光谱图像，l表示拍摄的低分辨率超光谱图像，||·||f表示矩阵的frobenius范数。

步骤206：使用对齐模型求解算法求解对齐模型，对矩阵形式的单应变换进行更新。

所述的对齐模型求解方法优选lucas-kanade方法、运动估计方法、基于傅里叶变换的对齐方法等。

其中lucas-kanade方法可以通过迭代的方式求解单应变换矩阵。为了加快迭代的收敛速度，lucas-kanade组合算法和反向组合算法等变种也同样适用于本问题的求解。

步骤207：根据更新后的单应变换矩阵，对所述的高分辨率rgb图像进行变换。

步骤208：迭代进行步骤203至步骤207所述的超光谱重建和对齐过程，提高图像对齐的精确度和超光谱重建的精度，直到达到预设的迭代次数。迭代结束后，步骤203中得到的超光谱图像，即为最终的超光谱成像结果。

有益效果：

现有技术中没有适用于超光谱成像的图像融合平台中的高分辨率rgb图像和低分辨率超光谱图像的对齐方法，本发明公开的两种用于超光谱成像平台中双相机图像对齐的方法。

第一种用于超光谱成像平台中双相机图像对齐的方法有益效果为：提供一种针对低分辨率超光谱图像和高分辨率rgb图像的对齐方法，通过图像对齐能够提高基于图像融合平台的超光谱成像算法的精度。

第二种用于超光谱成像平台中双相机图像对齐的方法有益效果为：提供一种适用于超光谱成像的图像融合平台中的高分辨率rgb图像和低分辨率超光谱图像的对齐方法，通过超光谱重建和对齐过程的迭代，能够提高图像对齐的精确度和超光谱重建的精度。

附图说明

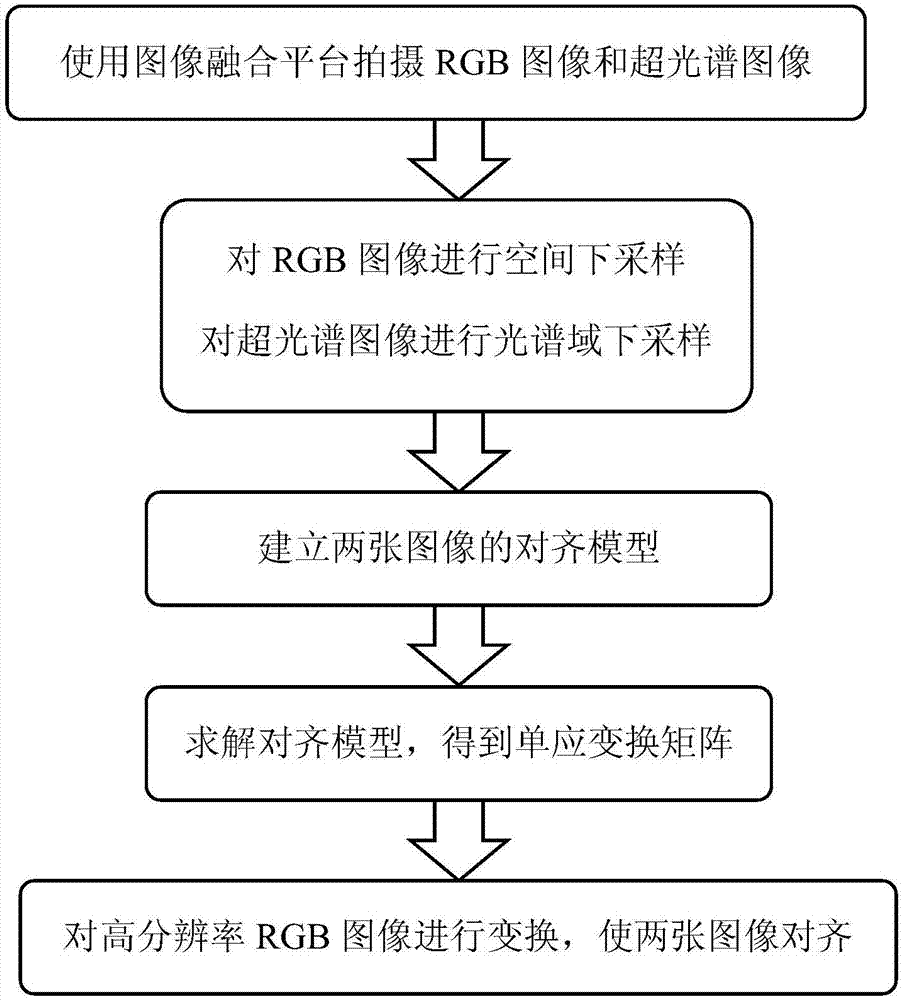
图1是本发明中用于超光谱成像平台中双相机图像对齐的方法的流程图。

图2是本发明中用于超光谱成像平台中双相机图像对齐的另一种方法的流程图。

图3是本发明中对齐方法适用的图像融合平台的示意图。

图4是本发明中对齐过程的示意图。

具体实施方式

为了更好的说明本发明的目的和优点，下面结合附图和实例对发明内容做进一步说明。

实施例1：

本实施例公开的一种用于超光谱成像平台中双相机图像对齐的方法，应用于超光谱成像的图像融合平台，使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像；对rgb图像进行空间下采样得到低分辨率rgb图像，对超光谱图像进行光谱域下采样得到与空间下采样相同尺寸的低分辨率rgb图像；对所述的两张低分辨率rgb图像建立图像对齐模型；使用对齐模型求解算法求解对齐模型中的单应变换矩阵；使用所述单应变换矩阵，对所述高分辨率rgb图像进行变换，使高分辨率rgb图像与所述低分辨率超光谱图像对齐，从而提高基于图像融合平台的超光谱成像算法的精度。以上方法的流程图如图1所示。

在图像融合平台中，双相机必须保证采集的是相同场景的图像，否则基于图像融合平台的各种超光谱成像方法的性能都会有不同程度的下降。因此，图像融合平台除了在硬件上需要使两个相机对齐之外，对于拍摄到的图像，也应该使用软件的方式进行进一步对齐。图像融合平台的示意图如图3所示。

对于两张相同场景但没有对齐的二维图像，它们之间的几何形变通常由一个变换矩阵来表示。常见的变换类型有：平移变换、欧氏变换、相似变换、仿射变换、投影(单应)变换等。在图像融合平台中，为了简化对齐的过程，本实施例中的对齐方法假设两张图像之间的变换为以上几种变换中的一种。这些变换都可以通过一个三维方阵来表示(详见szeliskir.imagealignmentandstitching:atutorial[j].foundationsandtrendsincomputergraphicsandvision,2006,2(1):1-104.)。

如图2所示，本实施例公开的一种用于超光谱成像平台中双相机图像的对齐方法，包括以下步骤：

步骤101：使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像。

步骤102：对rgb图像进行空间下采样得到低分辨率rgb图像，对超光谱图像进行光谱域下采样得到与空间下采样相同尺寸的低分辨率rgb图像。

步骤103：根据图像对齐模型对步骤2所述的两张低分辨率rgb图像进行对齐处理。

步骤103所述的图像对齐模型优选公式(1)所述的图像对齐模型：

其中t表示待求单应变换，x表示二维平面上的坐标点，y表示所述高分辨率rgb图像，h表示所述低分辨率超光谱图像的空间下采样矩阵，p代表rgb相机光谱响应曲线，即光谱域下采样矩阵，||·||f表示矩阵的弗罗宾尼斯(frobenius)范数。

上述模型要求高分辨率rgb图像和低分辨率超光谱图像具有完全相同的辐射强度。但是在实际应用中，两台相机因为硬件原因，总体亮度上通常会存在差别，因此，步骤103所述的图像对齐模型优选增强相关系数模型，即如公式(2)所述的图像对齐模型：

步骤104：根据对齐模型求解方法求解步骤3所述的图像对齐模型，得到矩阵形式的单应变换。

所述的对齐模型求解方法优选lucas-kanade方法、运动估计方法、基于傅里叶变换的对齐方法等。

其中lucas-kanade方法可以通过迭代的方式求解单应变换矩阵。为了加快迭代的收敛速度，lucas-kanade组合算法和反向组合算法等变种也同样适用于本问题的求解。关于lucas-kanade方法详见(bakers,matthewsi.lucas-kanade20yearson:aunifyingframework[j].internationaljournalofcomputervision,2004,56(3):221-255.)。

步骤105：根据所述单应变换矩阵，对所述高分辨率rgb图像进行变换，使高分辨率rgb图像与所述低分辨率超光谱图像对齐。

通过图像对齐能够提高基于图像融合平台的超光谱成像算法的精度。

实施例2：

本实施例还公开一种用于超光谱成像平台中双相机图像对齐的方法，应用于超光谱成像的图像融合平台，使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像；把单应变换矩阵初始化为单位矩阵；迭代进行以下超光谱重建和对齐的步骤，直至达到预设的迭代次数：对所述高分辨率rgb图像和低分辨率超光谱图像使用图像融合算法进行超光谱图像重建，得到重建的超光谱图像；对重建的超光谱图像进行空间下采样；对采集的低分辨率超光谱图像和空间下采样后的重建的超光谱图像，建立对齐模型；使用对齐模型求解算法，更新所述单应变换矩阵；使用更新后的单应变换矩阵对所述高分辨率rgb图像进行变换。通过上述超光谱重建和对齐的迭代步骤，能够提高图像对齐的精确度和超光谱重建的精度。以上方法的流程图如图2所示。

在图像融合平台中，双相机必须保证采集的是相同场景的图像，否则基于图像融合平台的各种超光谱成像方法的性能都会有不同程度的下降。因此，图像融合平台除了在硬件上需要使两个相机对齐之外，对于拍摄到的图像，也应该使用软件的方式进行进一步对齐。图像融合平台的示意图如图3所示。

对于两张相同场景但没有对齐的二维图像，它们之间的几何形变通常由一个变换矩阵来表示。常见的变换类型有：平移变换、欧氏变换、相似变换、仿射变换、投影(单应)变换等。在图像融合平台中，为了简化对齐的过程，本实施例中的对齐方法假设两张图像之间的变换为以上几种变换中的一种。这些变换都可以通过一个三维方阵来表示(详见szeliskir.imagealignmentandstitching:atutorial[j].foundationsandtrendsincomputergraphicsandvision,2006,2(1):1-104.)。

传统的图像对齐方法在进行两张图像的对齐时，一般要求两张图像具有较大的重合，也即几何形变的程度不能太大，而图像融合平台拍摄的两张图像之间最多具有32倍的分辨率差别。显然不能满足这种要求。因此，本实施例公开一种用于超光谱成像平台中双相机图像的对齐方法，利用如下相等关系：

y(x)h＝pl(t(x))

其中y表示高分辨率rgb图像，h表示空间下采样矩阵，l表示低分辨率超光谱图像，p表示rgb相机的光谱响应曲线，x代表二维空间坐标点，t表示几何形变。即如果对高分辨率rgb图像进行空间下采样，对低分辨率超光谱图像进行光谱域下采样，下采样后的两张图像能够满足传统图像对齐方法的要求。

根据对图像融合平台的特点的分析，本实施例还公开一种用于超光谱成像平台中双相机图像对齐的方法，包括以下步骤：

步骤201：使用超光谱相机获取场景的低分辨率超光谱图像，同时使用rgb相机获取相同场景的高分辨率rgb图像。

步骤202：把单应变换矩阵进行初始化，设置为单位矩阵。

步骤203：对获取的高分辨率rgb图像和低分辨率超光谱图像通过图像融合算法进行超光谱图像重建，得到重建的超光谱图像。图像融合算法优选：基于稀疏矩阵分解的图像融合算法(详见kawakamir,matsushitay,wrightj,etal.high-resolutionhyperspectralimagingviamatrixfactorization[c]//computervisionandpatternrecognition(cvpr),2011ieeeconferenceon.ieee,2011:2329-2336.)，基于空间-光谱稀疏表达的图像融合算法(详见akhtarn,shafaitf,miana.sparsespatio-spectralrepresentationforhyperspectralimagesuper-resolution[c]//europeanconferenceoncomputervision.springerinternationalpublishing,2014:63-78.)，基于成对图像光谱分解的图像融合算法(详见lanarasc,baltsaviase,schindlerk.hyperspectralsuper-resolutionbycoupledspectralunmixing[c]//proceedingsoftheieeeinternationalconferenceoncomputervision.2015:3586-3594.)，基于非负结构化稀疏表达的图像融合算法等(详见dongw,fuf,shig,etal.hyperspectralimagesuper-resolutionvianon-negativestructuredsparserepresentation[j].ieeetransactionsonimageprocessing,2016,25(5):2337-2352.)。

步骤204：对重建的超光谱图像进行空间下采样，使它的空间分辨率与采集的低分辨率超光谱图像一致。

步骤205：对采集的低分辨率超光谱图像和空间下采样后的重建的超光谱图像，根据对齐模型进行对齐处理。

步骤205所述的对齐模型优选公式(3)所示对齐模型。

其中t表示待求单应变换，x表示二维平面上的坐标点，l′表示所述空间下采样后的重建的超光谱图像，l表示拍摄的低分辨率超光谱图像，||·||f表示矩阵的frobenius范数。

步骤206：使用对齐模型求解算法，求解公式(3)所示的对齐模型，对矩阵形式的单应变换进行更新。所述的对齐模型求解方法优选lucas-kanade方法、运动估计方法、基于傅里叶变换的对齐方法等。

其中lucas-kanade方法可以通过迭代的方式求解单应变换矩阵。为了加快迭代的收敛速度，lucas-kanade组合算法和反向组合算法等变种也同样适用于本问题的求解。

步骤207：根据更新后的单应变换矩阵，对所述的高分辨率rgb图像进行变换。

步骤208：迭代进行步骤203至步骤207所述的超光谱重建和对齐过程，提高图像对齐的精确度和超光谱重建的精度，直到达到预设的迭代次数。迭代结束后，步骤203中得到的超光谱图像，即为最终的超光谱成像结果。

以上所述的具体描述，对发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。