视频卫星的点状运动目标状态估计方法及系统与流程

本发明涉及运动目标状态估计技术领域，特别是涉及一种视频卫星的点状运动目标状态估计方法及系统。

背景技术：

随着遥感应用的深入，应用需求已从定期的静态普查向实时高动态监测方向发展，利用卫星对全球热点区域和目标进行持续监测，获取动态信息已经成为迫切需求。除了经典光学遥感卫星影像包含的静态信息外，卫星视频还可以获取一定时空范围内的实时动态信息，使得遥感观测有更广阔的应用前景。视频应用中，针对点状运动目标的运动状态估计是动态信息定量化描述的重要一步，同时也是后期高级应用和处理的基础和前提。

当捕获到卫星视频中的点状运动目标后，能够实现运动目标在像方的识别。但无法实现运动目标在物方的运动状态估计，需要根据摄影测量原理，将序列影像上的目标点进行星地一体化求解，从而使得运动轨迹解算到物方空间，实现点状运动目标的可发现可跟踪可预测。

技术实现要素：

本发明的目的是提供一种基于rpc模型的视频卫星的点状运动目标状态估计方法及系统。

本发明的技术方案如下：

一、视频卫星的点状运动目标状态估计方法，包括步骤：

s1从视频卫星影像产品读取帧序列点文件，获得点状运动目标的坐标信息、每帧影像获取时间和每帧影像对应的rpc模型参数，并统计点状运动目标数；

s2利用每帧影像对应的rpc模型参数，构建每帧影像的rpc模型(x,y,h)表示影像像素(s,l)的正则化地面点坐标，即物方坐标；(x,y)表示影像像素(s,l)的正则化像点坐标；numl(p,l,h)、denl(p,l,h)、nums(p,l,h)、dens(p,l,h)为rpc模型的三次多项式；

s3对每帧影像上每一个点状运动目标，结合dem数据和每帧影像的rpc模型，分别计算各点状运动目标的物方坐标(x,y,h)；

s4根据点状运动目标的物方坐标(x,y,h)，采用切比雪夫多项式模型进行运动轨迹拟合；本步骤进一步包括：

4.1基于切比雪夫多项式构建点状运动目标的轨迹模型：

式(1)中，x(t)、y(t)、h(t)表示时刻t的物方坐标，t∈[t0,t0+δt]，t0表示起始历元时刻，δt表示拟合时间长度；n表示切比雪夫多项式的阶数，i表示每项切比雪夫多项式的阶数；分别表示卫星位置的x坐标分量、y坐标分量、h坐标分量的i阶切比雪夫多项式系数；ti(τ)表示i阶切比雪夫多项式，ti+1(τ)＝2τti(τ)-ti-1(τ)，t0(τ)＝1，t1(τ)＝τ，

4.2基于切比雪夫多项式构建误差方程：

式(2)中：xk、yk、hk表示视频卫星的第k个观测值；为观测值xk、yk、hk的改正值，τk为观测值xk所对应的τ值；

4.3利用最小二乘法求解误差方程，获得切比雪夫多项式系数带入式(1)，即可获得点状运动目标的运动轨迹模型；

s5利用点状运动目标的轨迹模型估计点状运动目标任意时刻的运动状态。

s3进一步包括：

3.1将rpc模型改为从像方到物方的正算形式模型

3.2迭代计算各点状运动目标对应的地面点的三维空间坐标，即物方坐标；

本子步骤具体包括

①给高程初始值h0；

②利用正算形式模型计算成像光线与当前高程面的交点pj的平面坐标，当前高程面的初始值为h0，j的初始值为1；

③利用pj的平面坐标在dem数据中内插出pj'点的高程，以该高程作为当前高程面的高程值，令j＝j+1，重复执行子步骤②；

④重复子步骤②～③，直至收敛，当前的pj'点即地面点，输出其三维空间坐标。

进一步的，s5包括：

基于点状运动目标的轨迹模型，对时刻t求一阶偏导，即获得点状运动目标的速度模型，采用速度模型估计点状运动目标任意时刻的速度。

进一步的，s5包括：

基于点状运动目标的轨迹模型，获取时刻t0的点状运动目标的平面坐标，记为(x0,y0)；增加极小值δt，获取点状运动目标时刻(t0+δt)的平面坐标，记为(x1,y1)，则点状运动目标时刻t0的瞬时切线方向角为

二、视频卫星的点状运动目标状态估计系统，包括：

读取模块，用来从视频卫星影像产品读取帧序列点文件，获得点状运动目标的坐标信息、每帧影像获取时间和每帧影像对应的rpc模型参数，并统计点状运动目标数；

rpc模型构建模块，用来利用每帧影像对应的rpc模型参数，构建每帧影像的rpc模型(x,y,h)表示影像像素(s,l)的正则化地面点坐标，即物方坐标；(x,y)表示影像像素(s,l)的正则化像点坐标；numl(p,l,h)、denl(p,l,h)、nums(p,l,h)、dens(p,l,h)为rpc模型的三次多项式；

物方坐标计算模块，用来对每帧影像上每一个点状运动目标，结合dem数据和每帧影像的rpc模型，分别计算各点状运动目标的物方坐标(x,y,h)；

运动轨迹拟合模块，用来根据点状运动目标的物方坐标(x,y,h)，采用切比雪夫多项式模型进行运动轨迹拟合；

所述的运动轨迹拟合模块进一步包括轨迹模型构建模块、误差方程构建模块和误差方程求解模块，其中：

轨迹模型构建模块，用来基于切比雪夫多项式构建点状运动目标的轨迹模型：

式(1)中，x(t)、y(t)、h(t)表示时刻t的物方坐标，t∈[t0,t0+δt]，t0表示起始历元时刻，δt表示拟合时间长度；n表示切比雪夫多项式的阶数，i表示每项切比雪夫多项式的阶数；分别表示卫星位置的x坐标分量、y坐标分量、h坐标分量的i阶切比雪夫多项式系数；ti(τ)表示i阶切比雪夫多项式，ti+1(τ)＝2τti(τ)-ti-1(τ)，t0(τ)＝1，t1(τ)＝τ，

误差方程构建模块，用来基于切比雪夫多项式构建误差方程：

式(2)中：xk、yk、hk表示视频卫星的第k个观测值；为观测值xk、yk、hk的改正值，τk为观测值xk所对应的τ值；

误差方程求解模块，用来利用最小二乘法求解误差方程，获得切比雪夫多项式系数带入式(1)，即可获得点状运动目标的运动轨迹模型；

运动状态估计模块，用来利用点状运动目标的轨迹模型估计点状运动目标任意时刻的运动状态。

和现有技术相比，本发明具有如下特点和有益效果：

(1)采用通用传感器模型作为卫星视频影像的几何定位处理模型，形式简单，使用方便；因此，本发明可有效地对卫星相关载荷、姿态、轨道、卫星相机等参数进行保密，同时让缺少专业知识的操作者可以方便的进行数据处理。

(2)采用视频卫星的凝视成像模式，能够解决星载视频影像点状动目标真实运动状态难以精确描述的问题。

(3)本发明可广泛应用于卫星视频的点状运动目标状态估计。

附图说明

图1是本发明的具体流程图；

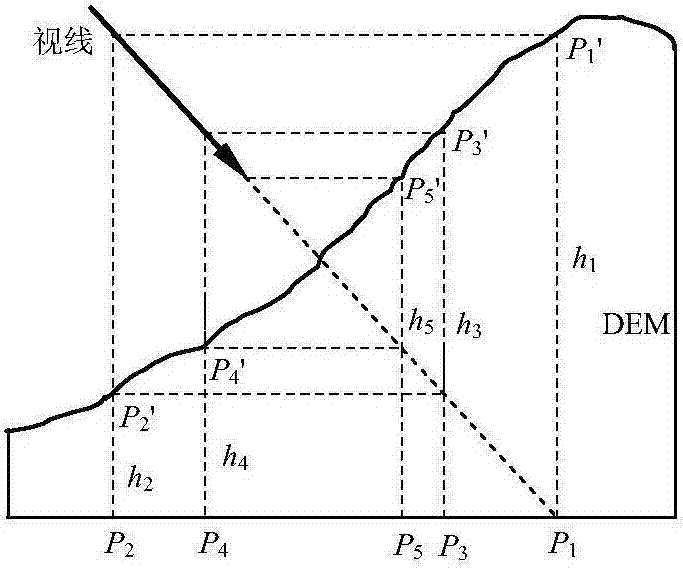
图2是dem辅助单像目标定位迭代计算原理。

具体实施方式

下面将结合图1对本发明进行详细的描述，具体包括以下步骤：

步骤1，读取视频卫星高级影像产品中已经检测出的帧序列点文件，统计点状运动目标数，并将点状运动目标的坐标信息和每帧获取时间存成相应的点文件；将每帧影像所对应的rpc模型参数存成相应的模型文件。rpc模型参数来自影像产品的rpc文件。

步骤2，利用每帧影像的rpc文件里的rpc模型参数，构建每帧影像的rpc模型。

rpc模型定义如下：

式(1)中：

(x,y)表示正则化的影像坐标；

(p,l,h)为正则化的地面点坐标；

numl(p,l,h)、denl(p,l,h)、nums(p,l,h)、dens(p,l,h)为三次多项式：

numl(p,l,h)＝a1+a2l+a3p+a4h+a5lp+a6lh+a7ph+a8l²+a9p²

+a10h²+a11plh+a12l³+a13lp²+a14lh²+a15l²p+a16p³+a17ph²；

+a18l²h+a19p²h+a20h³

denl(p,l,h)＝b1+b2l+b3p+b4h+b5lp+b6lh+b7ph+b8l²+b9p²

+b10h²+b11plh+b12l³+b13lp²+b14lh²+b15l²p+b16p³+b17ph²；

+b18l²h+b19p²h+b20h³

nums(p,l,h)＝c1+c2l+c3p+c4h+c5lp+c6lh+c7ph+c8l²+c9p²

+c10h²+c11plh+c12l³+c13lp²+c14lh²+c15l²p+c16p³+c17ph²；

+c18l²h+c19p²h+c20h³

dens(p,l,h)＝d1+d2l+d3p+d4h+d5lp+d6lh+d7ph+d8l²+d9p²

+d10h²+d11plh+d12l³+d13lp²+d14lh²+d15l²p+d16p³+d17ph²。

+d18l²h+d19p²h+d20h³

三次多项式的系数a1,...,a20，b1,...,b20，c1,...,c20，d1,...,d20是rpc文件中提供的模型参数，b1和d1通常为1；

l,s分别为影像列数值和行数值。

所谓正则化，是一项处理无限大、发散以及一些不合理表示式的方法，其方法透过引入一项辅助性的概念——正则化因子。在rpc模型中运用这种方法对地面点和影像点的坐标进行处理。

正则化地面点坐标定义为：

式(2)中：

lat_off、lat_scale、long_off、long_scale、height_off、height_scale为正则化因子，来自影像产品的rpc文件；

latitude表示经度，longitude表示纬度，height表示绝对高程，本文中简记为“高程”，经度、纬度和高程构成地面点的空间坐标。

正则化的影像坐标定义为：

式(3)中：

samp_off、samp_scale、line_off、line_scale为正则化因子，来自影像产品的rpc文件；

sample代表影像列坐标，其数值即为s；line代表影像行坐标，其数值即为l；即影像像素坐标采用(s,l)表示。

基于rpc模型具有模拟精度高，通用性好，应用方便，计算量小等等优点，但是，该模型同时存在一大缺点，即参数没有严格的几何意义，在进行对地目标几何定位处理时，无需建立起对应具有物理意义的严密模型。

步骤3，针对视频序列中每帧影像上的每一个点状运动目标，进行基于rpc模型的对地目标定位，引入数字高程模型(dem)，计算每个点状运动目标的物方坐标。

本步骤具体为：

利用卫星视频影像进行对地目标定位，实质上就是求解像点视线与数字高程模型的交点，将rpc模型改为从像方到物方的正算形式，如下：

式(4)中：

(x,y,h)为正则化的地面点坐标，即物方坐标；(x,y)为正则化的像点坐标。

已知dem数据时，点状运动目标的物方坐标(x,y,h)可通过逐次迭代计算方法求得，见图2，具体步骤包括：

①给定地面点的高程初始值h0；

②根据点状运动目标的像点坐标和当前高程面的高程值，利用公式(4)计算成像光线与当前高程面的交点pj的平面坐标(x,y)，当前高程面的初始值为h0，j的初始值为1；

③利用pj的平面坐标在dem数据中内插出pj'点的高程，以该高程作为当前高程面的高程值，令j＝j+1，重复执行子步骤②；

④重复子步骤②～③，直至收敛，当前的pj'点即地面点，输出其三维空间坐标，即物方坐标(x,y,h)。

重复子步骤②～③，依次获取系列点p1'、p2'、p3'……pi'，pi'即地面点，收敛条件可以为迭代次数达到预设的最大迭代次数，或两次迭代的pj的距离小于预设的距离阈值。

步骤4，根据各点状运动目标的物方坐标，采用切比雪夫多项式模型，对点状运动目标对应的地面点进行运动轨迹拟合，获得点状运动目标的轨迹模型。

切比雪夫多项式是定义在区间[-1,1]上的权函数为的正交多项式tn(p)＝cos(narccosp)，p表示待拟合的离散点。

切比雪夫多项式的递推关系如下式所描述：

tn+1(p)＝2ptn(p)-tn-1(p)(5)

由t0(p)＝1，t1(p)＝p递推可得：

显然，tn(p)的首项系数an＝2^n-1。

假设需要在时间间隔[t0,t0+δt]内计算n阶切比雪夫多项式的系数，t0表示起始历元时刻，δt表示拟合时间长度。

首先，将变量t∈[t0,t0+δt]]变换成τ∈[-1,1]：

则点状运动目标的物方坐标(x,y,h)的切比雪夫多项式，即轨迹模型如下：

式(8)中：

n表示切比雪夫多项式的阶数，n值自行设置，n值越大，精度越高，同时会增加计算开销，其值一般不超过20；i表示每项多项式的阶数；

分别表示点状运动目标的x坐标分量、y坐标分量、h坐标分量的切比雪夫多项式系数；

ti(τ)根据公式(5)递推获得。

以x坐标分量为例说明本步骤的具体实施过程。

设xk为视频卫星的观测值，构建误差方程：

式(9)中，xk表示第k个观测值，k＝1,2,...,m，m为观测值数量；为观测值xk的改正值，τk为观测值xk所对应的τ值。

误差方程的矩阵展开式如下:

令：

fx＝[x1x2x3...xm]^t；

则式(10)可写成向量表达式，如下：

vx＝bm-fx(11)

利用最小二乘误差原理，式(11)中的m须满足v^tpv＝min，p表示观测值的权函数，v^tpv＝min表示使v^tpv最小，则有：

b^tbm-b^tfx＝0(12)

可解得：

m＝n^-1fx(13)

式(13)中，n^-1＝(b^tpb)^-1。

这样，m各分量记为切比雪夫多项式系数同理，可以计算出任意一个点状运动目标地面的y坐标分量、h坐标分量在[t0,t0+δt]时间区间内的切比雪夫多项式系数利用这些系数，根据式(8)可以计算出[t0,t0+δt]时间区间内任意时刻的点状运动目标的物方坐标。

步骤5，根据点状运动目标的轨迹模型，对点状运动目标进行任意时刻的运动状态估计。

基于点状运动目标的轨迹模型后，对时刻t进行一阶偏导，即可获取点状运动目标的速度模型。

基于点状运动目标的轨迹模型，任意截取某一时刻t0的点状运动目标的平面坐标，记为(x0,y0)；增加极小值δt，得到点状运动目标时刻(t0+δt)的平面坐标，记为(x1,y1)。则点状运动目标时刻t0的瞬时切线方向角为θ：