一种基于自适应特征降维的多标记数据分类方法与流程
本发明属于机器学习
技术领域:
,涉及一种基于自适应特征降维的多标记数据分类方法,用于数据挖掘和大数据中,对包含噪声、特征复杂的多标记数据进行分类。
背景技术:
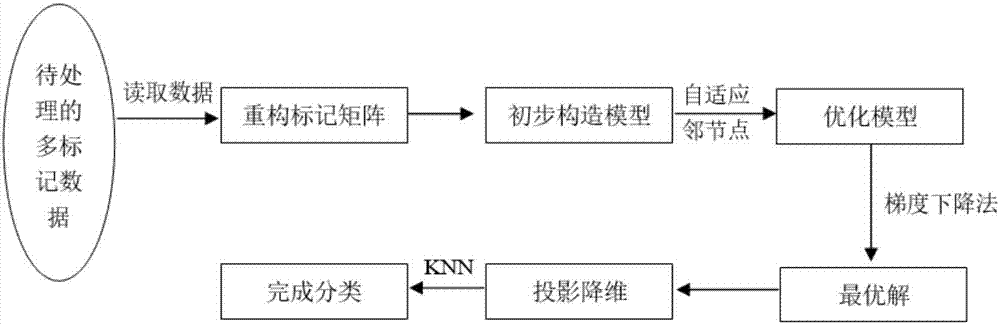
:随着计算能力、存储、网络的高速发展,人类积累的数据量正以指数速度增长。对于这些数据,人们迫切希望从中提取出隐藏其中的有用信息,更需要发现更深层次的规律,对决策,商务应用提供更有效的支持。为了满足这种需求,数据挖掘技术的得到了长足的发展,而多标记数据的分类在数据挖掘中是一项非常重要的任务,目前在商业上应用最多。多标记数据,是指数据中一个样本同时属于多个类别,例如在图像分类任务中,一个图像同时包含“山川”和“河流”,一个文件可能同时属于“环保”和“健康”类别,一个基因同时属于“变异基因”和“复制基因”。多标记数据的特征是人为规定,多标记是先验信息,事前已知的。数据特征是指人为规定的对数据的描述方法,例如图像数据,特征可以是每个图像样本的像素的灰度值所组成的矩阵;文本数据,特征可以是每个文本样本的总字数,特定字符出现的频率等组成的矩阵。所获取的原始数据特征一般所处高维空间,包含信息冗余较大,应用于分类任务中,计算复杂度高,效率低,并且容易受噪声数据影响,准确度不高。因此,传统的分类方法不能很好的应用于数据挖掘的分类过程。技术实现要素:针对上述现有技术中存在的问题,本发明的目的在于,提供一种基于自适应特征降维的多标记数据分类方法,以解决现有的分类方法计算复杂度高,准确度低的缺点,提高分类任务的性能。为了实现上述任务,本发明采用以下技术方案:一种基于自适应特征降维的多标记数据分类方法,包括以下步骤:步骤一,读取已知分类的多标记数据,分别将已知分类的多标记数据的特征和标记存储为特征矩阵x和标记矩阵y;读取待分类的多标记数据,将待分类的多标记数据的特征存储为矩阵t;步骤二,将标记矩阵y重构为潜在语义矩阵v和系数矩阵b以降低标记矩阵y中噪声的影响;步骤三,引入投影矩阵w,利用截断范数构造降维模型如下:上式中,xi是特征矩阵x的第i行,n是特征矩阵x的行数,即特征矩阵x中的样本个数;vi是潜在语义矩阵v的第i行,||·||f是f-范数,||·||2是2-范数,α和γ是系数,取值范围为(0,1];步骤四,在降维模型中加入几何结构约束,以使降维前后数据的局部几何结构保持一致;步骤五,利用降维模型构造目标函数,采用梯度下降法对目标函数进行迭代,直到目标函数收敛,得到投影矩阵w的最优解;步骤六,对已知分类的多标记数据、待分类的多标记数据进行投影降维处理,并对降维后的数据进行分类处理,完成。进一步地,步骤二中进行标记矩阵y重构时需要满足的公式为:上式中,表示f-范数的平方,y为n×k的矩阵,v为n×c的矩阵,b为c×k的矩阵。n,c,k分别是矩阵中样本的个数、重构中聚类的个数、标记的个数。进一步地,步骤四的具体过程包括:步骤4.1,根据特征矩阵x计算相似度矩阵s的第i行第j列元素:上式中,xi、xj分别是特征矩阵x的第i行和第j列向量,σ2是特征矩阵x的方差;步骤4.2,定义拉普拉斯矩阵l:l=a-s其中对角矩阵a的第i行第i列元素n是相似度矩阵s中样本的个数;步骤4.3,加入几何结构约束,构造模型如下:上式中,β是系数,0<β≤1,tr(·)表示矩阵的迹,ε为参数,取值范围为(0,0.1]。进一步地,步骤五的具体过程包括:步骤5.1,构造目标函数j如下:为了方便求偏导数和迭代,对目标函数变形得:其中矩阵f的第i行第i列元素ind(·)表示满足条件值为1,不满足条件值为0;步骤5.2,目标函数j(w,v,b)分别对w,v,b求偏导数:步骤5.3,梯度下降过程,w、v、b的更新规则如下:其中,λv,λb,λw为梯度下降的步长,取值范围均为(0,1];步骤s54,对w、v、b分别赋予随机初值,代入目标函数j(w,v,b),求得的值记为;利用步骤s53中的变量更新规则,得到新的变量w',v',b',再代入目标函数j(w',v',b'),求得的值记为j';计算目标函数的下降程度g=j'-j,若g>10^-3,则循环上述步骤,直到g≤10^-3,此时输出投影矩阵w,即为最优化解。进一步地,步骤六中进行投影降维处理的过程为:根据步骤五中得到的投影矩阵w,已知分类的多标记数据特征矩阵x的自适应降维后的特征矩阵x',如下:x'=x*w待分类的多标记数据特征矩阵自适应降维后的特征矩阵t',如下:t'=t*w进一步地,步骤六中进行分类处理的过程为:计算特征矩阵t'中第i个样本与特征矩阵x'第j个样本之间的距离dij:dij=|x′i-t′j|i,j=1,2,…n其中n为特征矩阵x'中样本个数;对第i个样本与其他样本之间的距离进行升序排列:{di1,di2,di3…dik…din}然后统计距离第i个样本最近的个样本中,统计出现频率最多的类标记,即为第i个样本的所属分类。本发明与现有技术相比具有以下技术特点:1.本发明投影矩阵的最优化求解过程,对高维特征的数据,进行线性变换,投影到低维空间,有效的降低分类任务中数据的复杂程度,去除冗余特征,保留有辨识度的特征,很好的解决了传统方法导致计算复杂度高的问题,提高了数据分类的效率。2.本发明构造降维模型的过程,利用多标记数据的标记矩阵,通过聚类得到潜在语义信息,有效解决了原始数据中噪声对分类准确率的影响,提高了数据分类的准确率。附图说明图1为本发明方法的流程图;具体实施方式一、方法详细步骤本发明提供了一种基于自适应特征降维的多标记数据分类方法,包括以下步骤:步骤一,数据读取利用matlab读取已知分类的多标记数据,分别将已知分类的多标记数据的特征和标记存储为特征矩阵x和标记矩阵y;读取待分类的多标记数据,将待分类的多标记数据的特征存储为矩阵t;步骤二,重构标记矩阵将标记矩阵y重构为潜在语义矩阵v和系数矩阵b以降低标记矩阵y中噪声的影响;具体地:为了降低标记矩阵y中噪声的影响,将y重构为两个更低维度的潜在语义矩阵v和系数矩阵b。并且重构误差最小,需满足下式:上式中,表示f-范数的平方,y为n×k的矩阵,v为n×c的矩阵,b为c×k的矩阵。n,c,k分别是矩阵中样本的个数、重构中聚类的个数、标记的个数。特征矩阵和表即矩阵为同一个数据集不同方面的描述,其中的样本个数n是相同的。步骤三,构造降维模型引入投影矩阵w,利用截断范数构造降维模型如下:上式中,xi是特征矩阵x的第i行,n是特征矩阵x的行数,即特征矩阵x中的样本数;vi是潜在语义矩阵v的第i行,||·||f是f-范数,||·||2是2-范数,α和γ是系数,取值范围为(0,1];投影矩阵w是d×c的矩阵,d是样本特征的维数,c是重构中聚类的个数。降维模型中第一项和第三项就是表达对w的要求,第一项最小化公式要求投影矩阵w要使得投影后的特征矩阵与潜在语义矩阵的误差尽可能小,第三项f-范数要求投影矩阵w每一个元素都尽可能小,从而使得模型泛化能力强。因为潜在语义矩阵v减少了多标记矩阵y中噪声的影响,所以我们利用回归模型和潜在语义矩阵v的优势,构造上述降维模型同时进行了标记矩阵y的重构和降维,同时也加强了降维过程的鲁棒性。步骤四,在降维模型中加入几何结构约束,以使降维前后数据的局部几何结构保持一致;步骤4.1,根据特征矩阵x计算相似度矩阵s的第i行第j列元素:上式中,xi、xj分别是特征矩阵x的第i行和第j列向量,σ2是特征矩阵x的方差;步骤4.2,定义拉普拉斯矩阵l:l=a-s其中对角矩阵a的第i行第i列元素n是相似度矩阵s中样本的个数,也是行数或列数;矩阵的每个元素代表了任意两个样本之间的相似程度;步骤4.3,为了使降维前后数据的局部几何结构保持一致,加入几何结构约束,构造模型如下:上式中,β是系数,0<β≤1,tr(·)表示矩阵的迹,ε为参数,取值范围为(0,0.1],其余参数含义同步骤三中的降维模型。步骤五,利用步骤四处理后的降维模型构造目标函数,采用梯度下降法对目标函数进行迭代,直到目标函数收敛,得到投影矩阵w的最优解;步骤5.1,构造目标函数j如下:为了方便求偏导数和迭代,对目标函数变形得:其中矩阵f的第i行第i列元素ind(·)表示满足条件值为1,不满足条件值为0;骤5.2,目标函数j(w,v,b)分别对w,v,b求偏导数:步骤5.3,梯度下降过程,w、v、b的更新规则如下:其中,λv,λb,λw为梯度下降的步长,取值范围均为(0,1];根据目标函数的趋势确定,当目标函数下降太慢时,将步长调大,当步长过大,而导致目标函数上升时,再将步长调小。步骤s54,对w、v、b分别赋予随机初值,代入目标函数j(w,v,b),求得的值记为;利用步骤s53中的变量更新规则,得到新的变量w',v',b',再代入目标函数j(w',v',b'),求得的值记为j';计算目标函数的下降程度g=j'-j,若g>10^-3,则循环上述步骤,直到g≤10^-3,此时输出投影矩阵w,即为最优化解。步骤六,对已知分类的多标记数据、待分类的多标记数据进行投影降维处理,并对降维后的数据进行分类处理,完成;具体地:进行投影降维处理的过程为:根据步骤五中得到的投影矩阵w,已知分类的多标记数据特征矩阵x的自适应降维后的特征矩阵x',如下:x'=x*w待分类的多标记数据特征矩阵自适应降维后的特征矩阵t',如下:t'=t*w进行分类处理的过程为:计算特征矩阵t'中第i个样本与特征矩阵x'第j个样本之间的距离dij:dij=|x′i-t′j|i,j=1,2,…n其中n为特征矩阵x'中样本个数;对第i个样本与其他样本之间的距离进行升序排列:{di1,di2,di3…dik…din}然后统计距离第i个样本最近的个样本中,统计出现频率最多的类标记,即为第i个样本的所属分类。二、仿真实验对本发明中提出的多标记降维方法的仿真。仿真条件是matlabr2014b64位软件下进行。本实验以mrboutell等人于2004年在patternrecognition上发表的论文“learningmulti-labelsceneclassification”中的数据集scene作为仿真实验的数据,包含1211个训练样本,1196个测试样本,294维特征,6个标记。分别对比本发明方法与主成分分析(pca),线性判别式(lda),局部保持投影(lpp)将特征降低到100维后的在各标记上的分类准确率和总的时间耗费。表1本发明方法与pca、lda、lpp的准确率对比表2本发明方法与pca、lda、lpp的耗费时间对比方法pcaldalpp本发明方法时间(秒)1218218058结合表1和表2中的实验数据,本发明的多标记数据分类方法在4个标记的准确率都是高于其他三种方法,并且完成分类任务的时间成本明显低于其他方法。因此,实验结果表明,本发明在大多数情况下具有高准确率、高效率等优点。当前第1页12
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1