一种利用有限元建模计算柔性轴承疲劳寿命的方法与流程
本发明涉及柔性轴承疲劳寿命计算方法领域,具体是一种利用有限元建模计算柔性轴承疲劳寿命的方法。
背景技术:
谐波齿轮传动技术是上世纪50年代随航天技术的发展而产生的一种新的传动技术。谐波减速器主要由波发生器、柔轮、刚轮等组成。装有柔性轴承的凸轮波发生器是谐波传动主要采用的波发生器结构。
由于谐波齿轮传动的诸多独特优点,近几十年来,谐波减速器广泛应用在工业机器人、高档轿车、航空航天、光学仪器、通用机械等领域。柔性轴承作为谐波减速器的关键配套元件,柔性轴承的疲劳寿命是影响谐波减速器的寿命的重要因素之一。
柔性轴承不同于普通轴承,它的内外圈的壁厚薄,容易产生弹性变形,在未装入凸轮之前内外圈是圆形的。如图3所示,装上凸轮轴1之后,柔性轴承内圈2、柔性轴承外圈3变形为凸轮轴1廓线的等距曲线。
现有的柔性轴承疲劳寿命一般通过实验测得,这种方法成本高,实验时间长,且一般实验机对待测轴承的型号尺寸有限定,适用性不高。
而现有利用仿真计算疲劳寿命的方法都是以普通轴承为分析对象,这类轴承的内外圈在工作状态保持圆形,跟柔性轴承装配到凸轮情况套圈会发生大的弹性变形这一特点不同。现有的轴承仿真方法无法模拟柔性轴承装配到凸轮是套圈发生大的弹性变形这一过程,所以现有仿真方法不再适用于柔性轴承,目前也没有很好的柔性轴承仿真方法。
通过仿真方法预测柔性轴承的疲劳寿命,相比实验方法成本低,分析快,可适用不同型号的柔性轴承,缩短了柔性轴承设计开发周期,对谐波齿轮传动技术的推广应用和经济社会发展具有重要意义。
本发明提出一种利用有限元建模计算柔性轴承疲劳寿命的方法,如图1所示,利用link单元代替保持架,模拟保持架对滚动体的约束,由有限元仿真结果得到柔性轴承内部载荷分布,用于计算柔性轴承的当量滚动体载荷,从而计算柔性轴承的疲劳寿命。
技术实现要素:
本发明为克服现有技术的上述缺陷,提出一种利用有限元建模计算柔性轴承疲劳寿命的方法,该方法可以模拟柔性轴承装配到凸轮这个过程,同时该方法利用link单元代替轴承保持架简化了有限元模型,相比实验方法成本低,分析快,可适用不同型号的柔性轴承。
本发明采用的技术方案为:一种利用有限元建模计算柔性轴承疲劳寿命的方法,其特征在于,该方法实现步骤如下:
步骤1):ug(注:一种三维辅助设计软件)中画出柔性轴承和凸轮轴的几何立体模型,并且保存为bearing.stp格式;
步骤2):打开ansys(注:一种有限元力学仿真软件),导入bearing.stp几何立体模型,将内圈、外圈、滚动体、凸轮轴轴划分为六面体网格,并在凸轮轴-内圈,内圈-滚动体,外圈-滚动体之间设置接触关系;
步骤3):添加link单元代替轴承保持架;
步骤4):在有限元模型中施加载荷和约束;
步骤5):将有限元模型导入到工程分析软件ansys中,进行多体接触分析;
步骤6):导出ansys分析计算出的各个滚动体位置的法向接触反力,根据公式计算柔性轴承的当量滚动体载荷;
步骤7):根据l-p寿命理论(注:一种由lundberg和palmgren提出的计算轴承寿命的理论),计算柔性轴承的寿命。
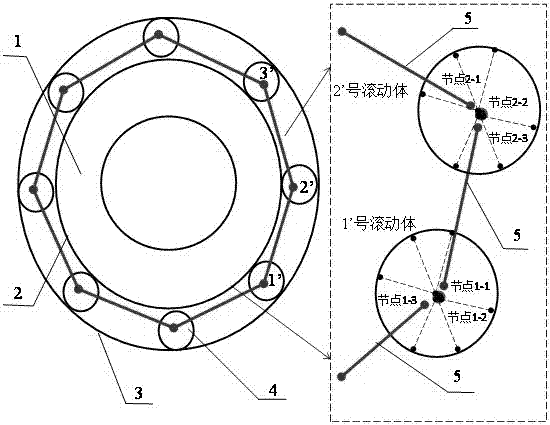
进一步的,所述的添加link单元代替轴承保持架,如图1、2所示,具体步骤如下:
步骤①:在每个滚动体的球心位置生成3个节点,1号滚动体生成的三个节点,节点名称可以称为1-1,1-2,1-3;2号滚动体生成的三个节点称为2-1,2-2,2-3…;柔性轴承滚动体个数为23,故共生成69个节点;
步骤②:上述生成的节点中,对相同位置的节点的平动自由度进行耦合,相同位置的节点的转动自由度可以不同;节点1-1、节点1-2、节点1-3的x、y、z三个方向的平动自由度相同,但转动自由度可以不同;
步骤③:将相邻的滚动体之间的节点相连形成link单元(5),连接方式为节点1-1与节点2-3相连,节点2-1与节点3-3相连…节点22-1与节点23-3相连,最后节点23-1与节点1-3相连,这些形成了23个link单元;
步骤④:将球心节点与球表面的节点建立多点约束mpc,使球表面节点的自由度与球心节点自由度相同,滚动体1’(4)表面的节点与节点1-2建立多点约束,滚动体2’(4)表面的节点与节点2-2建立多点约束…。
本发明的原理在于:
通过ug画出所需要的柔性轴承,将几何模型导入到有限元软件ansys中,对柔性轴承划分六面体网格,添加link单元代替轴承保持架,link单元可以模拟柔性轴承中保持架对滚动体的约束作用,柔性轴承装配到凸轮轴后,柔性轴承由图1(a)状态变为图1(b)状态。本专利提出了计算柔性轴承的寿命的新方法,通过link单元模拟轴承保持架约束,通过这种连接关系,柔性轴承可看做由内圈,外圈,凸轮轴,link单元连接球组成的“球链”这四个部分组成的系统。有限元仿真方法得到柔性轴承的载荷分布,从而计算柔性轴承的疲劳寿命。
本发明和现有技术相比的特点与优势为:
(1)本发明采用link单元来模拟保持架,实现在接触分析的过程中,相邻滚动体之间的距离保持不变,模拟了保持架对滚动体的约束作用,简化了有限元模型的规模,减少了有限元分析的计算量,增加了效率又不损失计算精度。
(2)仿真方法较实验方法成本低,分析快,缩短了柔性轴承设计开发周期
附图说明
图1为柔性轴承link单元模拟保持架的示意图(其中图(a)为圆形状态轴承,图(b)为弹性变形为椭圆形状态轴承)
图2为ansys中“实体-link单元”有限元模型(其中图(a)为整体轴承照片图,图(b)为局部放大图)
图3为柔性轴承示意图
图中标号:1-凸轮轴、2-内圈、3-外圈、4-滚动体、5-link单元
图4为ug中柔性轴承的模型
图5为柔性轴承的约束、载荷
具体实施方式
本发明的优化实施例几何附图之表述如下:
实施例一:参见图1~5,本发明利用有限元建模计算柔性轴承疲劳寿命的方法,其特征在于操作步骤如下:
步骤1):ug软件中画出柔性轴承和凸轮轴的几何立体模型,并且保存为bearing.stp格式;
步骤2):打开ansys软件,导入bearing.stp几何立体模型,将内圈(2)、外圈(3)、滚动体(4)、凸轮轴(1)划分为六面体网格,并在凸轮轴(1)-内圈(2),内圈(2)-滚动体(4),外圈(3)-滚动体(4)之间设置接触关系;
步骤3):添加link单元(5)代替轴承保持架;
步骤4):在有限元模型中施加载荷和约束;
步骤5):将有限元模型导入到工程分析软件ansys中,进行多体接触分析;
步骤6):导出ansys分析计算出的各个滚动体位置的法向接触反力,根据公式计算柔性轴承的当量滚动体载荷;
实施例二:本实施例与实施例一基本相同,特征之处如下:
所述的添加link单元代替轴承保持架的具体方法操作步骤为:
步骤①:在每个滚动体的球心位置生成3个节点,1号滚动体生成的三个节点,节点名称可以称为1-1,1-2,1-3;2号滚动体生成的三个节点称为2-1,2-2,2-3…;柔性轴承滚动体个数为23,故共生成69个节点;
步骤②:上述生成的节点中,对相同位置的节点的平动自由度进行耦合,相同位置的节点的转动自由度可以不同;节点1-1、节点1-2、节点1-3的x、y、z三个方向的平动自由度相同,但转动自由度可以不同;
步骤③:将相邻的滚动体之间的节点相连形成link单元(5),连接方式为节点1-1与节点2-3相连,节点2-1与节点3-3相连…节点22-1与节点23-3相连,最后节点23-1与节点1-3相连,这些形成了23个link单元;
步骤④:将球心节点与球表面的节点建立多点约束mpc,使球表面节点的自由度与球心节点自由度相同,滚动体1’(4)表面的节点与节点1-2建立多点约束,滚动体2’(4)表面的节点与节点2-2建立多点约束…。
以型号为csf_20_80谐波减速器中的柔性轴承为例说明。
步骤1):ug软件中画出柔性轴承和凸轮轴的几何立体模型(如图4),并且保存为bearing.stp格式;
步骤2):打开ansys软件,导入bearing.stp几何立体模型,将内圈(2)、外圈(3)、滚动体(4)、凸轮轴(1)划分为六面体网格,并在凸轮轴-内圈,内圈-滚动体,外圈-滚动体之间设置接触关系;
步骤3):添加link单元(5)代替轴承保持架,如图1、2所示。具体步骤如下:
(1)在每个滚动体(4)的球心位置生成3个节点,1’号滚动体(4)生成的三个节点,节点名称可以称为1-1,1-2,1-3;2’号滚动体生成的三个节点称为2-1,2-2,2-3。柔性轴承滚动体个数为23,故共生成69个节点;
(2)上述生成的节点中,对相同位置的节点的自由度进行耦合,如节点1-1,节点1-2,节点1-3这3个节点自由度相同;节点2-1,节点2-2,节点2-3这3个节点自由度相同…;
(3)将相邻的滚动体之间的节点相连形成link单元(5),连接方式为节点1-1与节点2-3相连,节点2-1与节点3-3相连…节点22-1与节点23-3相连,最后节点23-1与节点1-3相连,这些形成了23个link单元(5);
(4)将球心节点与球表面的节点建立多点约束mpc,使球表面节点的自由度与球心节点自由度相同,如1’号滚动体表面的节点与节点1-2建立多点约束,2’号滚动体表面的节点与节点2-2建立多点约束…。
步骤4):在有限元模型中施加载荷和约束,如图5,具体步骤如下:
(1)在长轴区域的柔性轴承外圈施加对称径向力;
(2)对凸轮轴施加固定约束。
步骤5):将有限元模型导入到工程分析软件ansys中,进行多体接触分析;
步骤6):导出ansys分析计算出的各个滚动体位置的法向接触反力,根据公式计算柔性轴承的当量滚动体载荷,具体步骤如下:
(1)ansys后处理中,导出每个滚动体与套圈之间的法向接触反力,记作qj;
(2)根据各个滚动体位置的法向接触反力,计算轴承内外套圈当量滚动体负荷。点接触时,轴承内外套圈当量滚动体负荷计算公式为:
其中,qei为轴承内圈当量滚动体负荷;qeo为轴承外圈当量滚动体负荷;j为滚动体编号;qj为第j个滚动体的法向接触反力;s,ω为负荷指数,对点接触,s=3,ω=10/3;z为滚动体个数。
步骤7):根据l-p寿命理论,计算柔性轴承的寿命,具体步骤如下:
(1)根据柔性轴承的各参数,计算内外套圈的额定滚动体载荷。内外套圈的额定滚动体载荷的计算公式为:
其中,qci为内圈额定滚动体负荷;qco为外圈额定滚动体负荷;a为经验系数,对轴承钢,a=98.1;r为滚动体母线的曲率半径;dw为滚动体直径;ri、re分别为内、外套圈沟曲率半径;dm为滚动体中心圆直径;γ为无量纲几何参数,γ=dw/dm;z为滚动体个数。
(2)根据内外套圈当量滚动体负荷qei、qeo和内外套圈的额定滚动体载荷qci、qco计算轴承的内外圈额定寿命。内外圈额定寿命的计算公式为:
其中,l10i、l10e分别为内外圈的额定寿命;ε为寿命指数,对点接触,ε=3。
(3)根据滚动轴承寿命参数weibull分布方程,整套轴承的额定寿命为:
其中,l10为整套轴承的额定寿命;e为weibull分布斜率,对点接触,e=10/9。
按照以上方法,即可计算柔性轴承的疲劳寿命。
本发明未详细阐述部分属于本领域技术人员的公知技术。
以上所述,仅为本发明中的具体实施方式,但本发明的保护范围并不局限于此,任何熟悉该领域的人在本发明所揭露的技术范围内,可理解想到的变换或替换,都应涵盖在本发明的包括范围之内。
- 还没有人留言评论。精彩留言会获得点赞!