一种运动目标下的辛时域有限差分电磁仿真方法与流程
本发明涉及一种地磁场数值计算基数,特别是一种运动目标下的辛时域有限差分电磁仿真方法。
背景技术:
在电磁数值仿真过程中,首先,辛时域有限差分法相对于传统的时域有限差分法,针对麦克斯韦方程,空间上采用的是高阶的离散格式,具有较高的计算精度和较低的数值色散,在满足同样精度的情况下可以使用比传统的时域有限差分法更粗的网格单元。
针对计算电大尺寸目标所采用的传统的时域有限差分法计算内存大,数值色散性差等缺点,jiayuanfang等提出了高阶时域有限差分法,该算法在时间上的离散方式与传统的fdtd算法是一样的,而在空间上的离散格式则使用高阶精度的,结果明显提高了数值色散特性及计算的精度,而且还保留了以往传统fdtd算法简单、直观的特点。可参考文献:(1)jiayuanfang,“alocallyconformedfinite-differencetime-domainalgorithmofmodelingarbitraryshapeplanarmetalstrips,”ieeetransactionsonmicrowavetheoryandtechniques,vol.41,no.5,pp:830-838,1989.和(2)theodorost.zygiridis,theodorosd.tsiboukis,“adispersion-reductionschemeforthehigherorder(2,4)fdtdmethod,”ieeetransactionsonmagnetics,vol.40,no.2,pp:1464-1467,march2004.
辛时域有限差分法在空间离散上实质就是采用了高阶时域有限差分法的高阶离散格式。而且,针对麦克斯韦方程组,在对时间的离散上,由于对于任意取定的时间,哈密尔顿方程组的初值问题解都为辛变换,所以存在许多内在的守恒量。随着时间t的增大,尽管数值解与精确解相比,难免会产生一些误差,却能够始终保持这个误差为一个常数。这种算法则称之为辛算法。可参考文献:(3)冯康,秦孟兆.哈密尔顿系统的辛几何算法[m].浙江:科学技术出版社.2003
麦克斯韦方程可被视为一个无穷维的哈密尔顿系统,而基于哈密尔顿系统的算法应该在辛几何框架内产生,并且随着时间的演化,推导出的离散算法应该永远是辛变换的,也就是说辛算法可以应用到对麦克斯韦方程组的离散计算中。可参考文献(4)haruoyoshida,“constructionofhigherordersymplecticintegrators,”physics.letters.a,vol.150,no.5,6,7,pp.262-268,november1990.和(5)etienneforest,ronaldd.ruth,“fourth-ordersymplectlcintegration,”physicad:nonlinearphenomena,vol.43,pp.105-117,1990.
传统的时域有限差分法破坏了麦克斯韦方程的辛结构,难免会引入人为耗散性而降低数值稳定性,使得哈密尔顿系统的总能量会随时间表现为线性变化,即计算误差会线性累积,最终导致计算的结果严重歪曲和失真。可参考文献(6)rrieben,dwhite,grodrigue,“high-ordersymplecticintegrationmethodsforfiniteelementsolutionstotimedependentmaxwellequation,”ieeetransactionsonantennasandpropagation,vol.52,no.8,pp.2190-2195,2004.
而辛时域有限差分法采用基于哈密尔顿系统的辛算子,可以降低高阶的离散格式下对数值稳定性的严格要求,进一步降低数值色散误差,提高计算精度。但是这样的辛时域有限差分法一般都是针对相对静止的目标来进行电磁仿真计算的,如果要应用到如高速运动的飞机、导弹,快速移动的汽车等运动目标上,就需要在原来麦克斯韦方程组中加入速度这个变量,改写整个方程组的离散格式。
技术实现要素:
本发明的目的在于提供一种运动目标下的辛时域有限差分电磁仿真方法,包括以下步骤:
步骤1,构建麦克斯韦方程组,采用辛时域有限差分法求解麦克斯韦方程组;
步骤2,引入运动目标的速度至麦克斯韦方程组,采用辛时域有限差分法求解此时麦克斯韦方程组。
采用上述方法,步骤2的具体过程为:
步骤2.1,引入运动目标的速度至麦克斯韦方程组,麦克斯韦方程组的本构关系变为
其中,v位运动目标速度,
步骤2.2,消除光速c对方程(5)的影响,方程简化为
j=σ·[e+v×b](6)
步骤2.3,针对磁场的差分格式为
步骤2.4,针对电场,从第n时间步到第n+1步,经过5次迭代,第s-1级迭代到s级的离散格式变为如下:
其中
gbx(i)=σ·δt/ε0
其中dx为x方向的电位移矢量分量,hy为y方向的磁场矢量分量,ex为x方向的电场矢量分量。ε=εrε0,εr为相对介电常数,ε0为真空介电常数;μ0为真空磁导率,s为辛传播子系数的级数,cs和ds为级数为s时的辛算子系数,,cfl为数值稳定性条件,δt为时间步长,δ为空间步长,并且δt和δ满足cfl条件。
本发明将运动目标的速度引入麦克斯韦方程组中,解决了辛时域有限差分法不能针对高速运动目标进行测量的弊端,用过该本发明建立的仿真,可以很好的描述流动中的运动目标的相关参数。
下面结合说明书附图对本发明作进一步描述。
附图说明
图1是本发明的方法流程图。
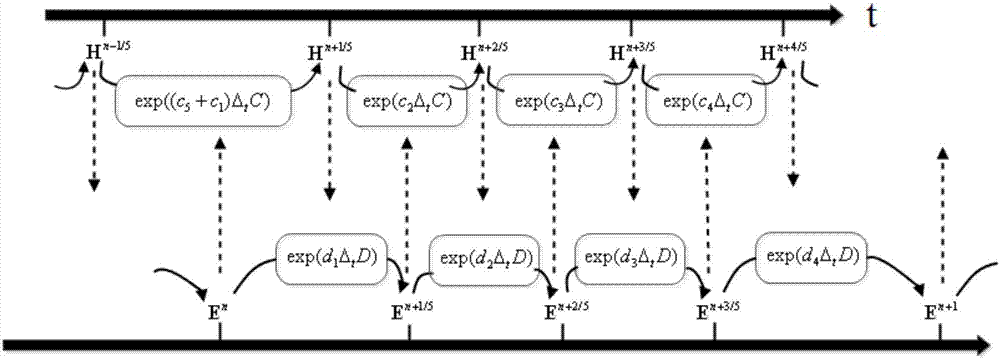
图2是本发明的sfdtd(5;4,4)算法的电磁场值迭代过程示意图。
图3是等离子体光子晶体模型示意图。
图4是流速分别为500mm/s,1000mm/s及静态下的等离子体光子晶体透射系数图谱示意图。
具体实施方式
结合图1,本发明涉及的一种运动目标下的辛时域有限差分电磁仿真方法,包括两大步骤:
步骤1,构建麦克斯韦方程组,采用辛时域有限差分法求解麦克斯韦方程组;
步骤2,引入运动目标的速度至麦克斯韦方程组,采用辛时域有限差分法求解此时麦克斯韦方程组。
其中,步骤1主要包括以下要点:
(1)用哈密尔顿函数hm表示的麦克斯韦方程组;
(2)在时间方向上用不同阶数辛算子对方程进行差分离散;
(3)在空间方向上用采用四阶精度的有限差分格式对方程进行离散;
(4)记m级p阶辛算法结合空间q阶的辛时域有限差分法为sfdtd(m:p,q),基于sfdtd(m:p,q)算法获取电磁场值随时间步长推进的方式。
具体地,电磁场中的麦克斯韦方程组可以用如下的哈密尔顿函数hm表示:
其中h和e分别为磁场和电场,ε和μ分别为媒质的介电常数和磁导率,▽为旋度。
通过变分法,从t=0到t=δt演化为:
其中,{0}3×3为3×3的零矩阵,r为三维旋度算子,ε为媒质的介电常数,μ为媒质的磁导率。通过上面的公式推导,即可以把适用于哈密尔顿系统的辛算法应用到求解麦克斯韦方程的辛时域有限差分法中来。
在时间方向上,用不同阶数的辛算子去近似:
其中,cl,dl为辛算子,m,p(m≥p)分别为辛算法的级数与阶数,下表展示了不同级数和阶数下的辛传播子系数。
表1不同级数和阶数下的辛传播子系数
在空间方向上,因为算符c,d中含有旋度算符r,所以为得到麦克斯韦方程的数值解,就必须在空间方向上对麦克斯韦方程做进一步离散。
目前采用四阶精度的离散近似为:
记m级p阶辛算法结合空间q阶的辛时域有限差分法为sfdtd(m:p,q),则基于sfdtd(5;4,4)算法的电磁场值随时间步长迭代的过程如图2所示。
步骤2中,将运动目标的速度v引入麦克斯韦方程组,麦克斯韦方程组的本构关系变为:
其中
由于运动目标的速度远小于光速,上式可简化为:j=σ·[e+v×b],由此可推出针对运动目标,速度v这个变量在磁场中的差分格式不变,所以在传统fdtd算法中,针对磁场的差分格式依旧保持不变,同时在fdtd(5;4,4)算法中,针对磁场的差分格式依然是原来的辛差分格式,如下:
而针对电场,在sfdtd(5;4,4)算法中,从第n时间步到第n+1步,经过5次迭代,第s-1级迭代到s级的离散格式变为如下:
其中:
gbx(i)=σ·δt/ε0
其中dx为x方向的电位移矢量分量,hy为y方向的磁场矢量分量,ex为x方向的电场矢量分量。ε=εrε0,εr为相对介电常数,ε0为真空介电常数;μ0为真空磁导率,s为辛传播子系数的级数,cs和ds为级数为s时的辛算子系数,,cfl为数值稳定性条件,δt为时间步长,δ为空间步长,并且δt和δ满足cfl条件。
由此完成针对动态目标的麦克斯韦方程组的求解。
实施例
本发明涉及的方法可以应用于高速飞行器轨迹测量问题中,特别是隐形高速飞行器的轨迹测量中。飞机采用等离子体隐身技术,将等离子体覆盖在飞行器体表上,可以达到隐身的效果。实际上等离子体就是一种光子晶体,等离子体光子晶体是由不同介质材料或真空和等离子体共同组成的人工周期性结构。其不仅具有不仅具有常规光子晶体的优点,可以对光的传播进行人为操控,而且具有光子禁带特性和光子局域态,可以很好地应用到高速飞行器,如隐身飞机上。而高速飞行器不是静态的目标,是带有较高速度的运动目标,这时就需要去考虑速度这个变量对于麦克斯韦方程组的影响。
8层介质和7层等离子体组成等离子体光子晶体模型,形成“介质-等离子体-介质”的结构,介质厚度等于等离子体厚度,等离子频率为2ghz,等离子体碰撞频率为2mrad/s,脉冲电磁波从模型左侧垂直入射,如图3所示。
整个等离子体光子晶体模型里的物质为流动的,其电导率为1s/m,流速分别为500mm/s,1000mm/s以及静态时,研究等离子体生物光子晶体带隙结构特性,得到的结果表明,增加流速对透射系数有一定的影响,流速越大,透射系数也相应地增大,仿真结果如图4所示。
- 还没有人留言评论。精彩留言会获得点赞!