非同步双星系统的稳定轨道计算方法与流程
本发明涉及一种非同步双星系统的轨道计算方法,特别涉及一种基于二阶微分修正的非同步双星系统稳定轨道的计算方法,属于航空航天技术领域,适用于探测器对非同步双星系统进行探测的轨道设计。
背景技术:
双小行星系统是特殊的一类小行星,系统由两颗相互绕质心环绕的小行星组成,同时系统的质心围绕太阳运行。双体小行星数量众多,大约占近地小行星和主带小行星数量的16%。对双星系统开展探测任务具有特别的科学回报,可以研究系统的演化以及动力学形成机理,验证YORP效应。此外,由于双星系统自身的特性,系统的物理参数可以利用地面观测进行估计,有效降低了探测任务的难度,因此对双星系统开展探测是未来深空探测的热点之一。根据双星系统的自旋和公转状态,可以将系统分为双同步系统,单同步系统和非同步系统,其中双同步系统中两个子星的自旋速度与相对运动的轨道角速度相同,单同步系统中子星之一的自旋速度与轨道角速度相同,而非同步系统中子星的自旋速度与轨道角速度均不相同,其中非同步双星系统在系统中所占的比例最高。对双星系统的环绕探测是小行星探测的重要组成部分。探测任务的设计中,需要对双星附近的轨道进行设计,搜索系统中的稳定轨道将是任务设计的基础。
目前双星系统内轨道的搜索方法中,在先技术【1】(参见Haibing Shang,Xiaoyu Wu,Pingyuan Cui.Periodic orbits in the doubly synchronous binary asteroid system and their applications in space missions[J].Astrophys Space Sci,2014,355:2154.)基于双椭球模型对双同步双星系统附近轨道进行了研究,利用对称性获得到大量可用于探测的周期轨道。但该方法只适用于双同步系统,对于自旋与公转不同步的系统将不适用。
在先技术【2】(参见乔栋,李翔宇,崔平远等,基于速度庞加莱截面双小行星系统周期轨道搜索方法,CN104477411A)利用速度庞加莱映射对周期轨道进行搜索,通过映射穿过X轴的位置可以得到相应的周期轨道。该方法同样只适用于自旋锁定的双星系统,对于非同步的系统将不适用。
技术实现要素:
本发明的目的是提出一种适用于非同步双星系统的稳定轨道计算方法,该方法先基于同步双星系统计算周期轨道,然后将同步系统中的周期轨道转换到非同步双星系统中,进行轨道积分,利用二阶微分修正算法获得长期稳定的轨道,具有初值易选取,收敛性好等特点。
本发明的目的是通过下述技术方案实现的。
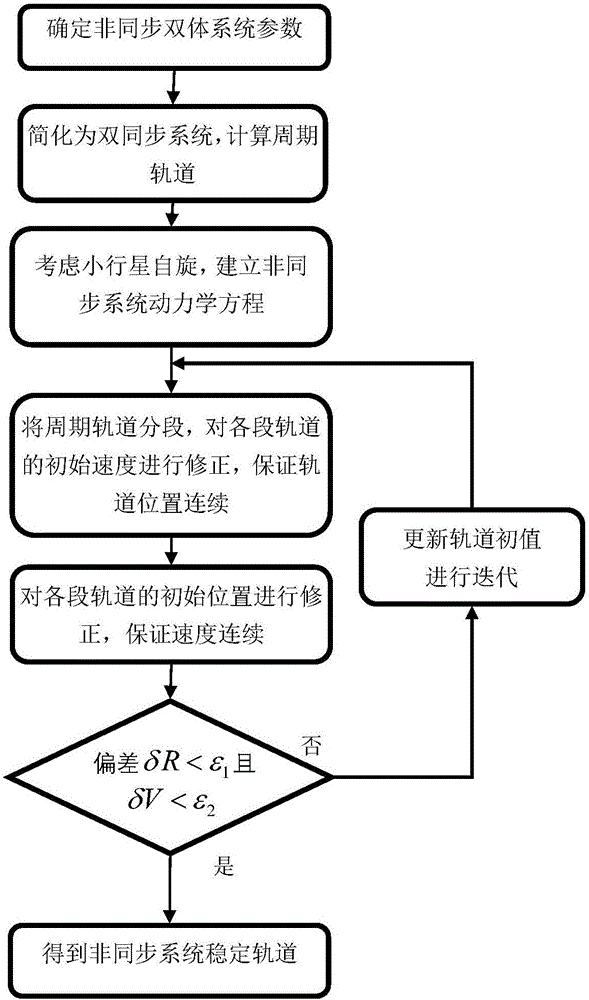
本发明公开的非同步双星系统的稳定轨道计算方法。对任意非同步双星系统,先将系统考虑为同步系统进行周期轨道搜索,然后根据小行星的自旋周期将同步系统转换为非同步系统并获得的周期轨道按轨道周期分成若干段,带入非同步系统中进行轨道积分,利用二阶微分修正对若干段轨道进行位置修正和速度修正,通过多次迭代获得非同步系统中的长期稳定轨道。能够实现适用于非同步双星系统的稳定轨道,且得到的轨道族多、收敛性好,计算效率高。
本发明公开的非同步双星系统的稳定轨道计算方法,包括以下步骤:
步骤一、根据确定的目标双星系统参数,忽略自旋角速度差别,将双星系统考虑为同步双星系统,建立椭球-椭球双星系统模型,在质心旋转坐标系下建立动力学模型。所述的双星系统参数包括双星的形状、质量比和相对距离。
其中ρ表示探测器到质心的位置矢量,ω为系统的旋转角速度,ρ1和ρ2为探测器到双星主星和子星的位置矢量。U1,U2表示双星的引力势能:
其中α,β,γ为星体的三个主轴长度,r1,r2为两个星体在质心旋转坐标系下的位置矢量。
步骤二、对同步双星系统进行周期轨道搜索,通过相应的搜索方法得到周期轨道族。
同步双星系统内的周期轨道满足利用双星系统模型的对称性能够对周期轨道的初始状态进行简化;对于面对称的轨道,轨道从OXZ平面出发,初值满足半个轨道周期后满足轴对称的轨道,轨道从X轴出发,初值满足半个轨道周期后应满足根据已有的搜索方法对双星系统内的区域进行搜索得到不同轨道周期和轨道能量的周期轨道族。
已有的搜索方法包括利用速度庞加莱映射或网格搜索。
步骤三、根据双星系统的自旋速度,建立非同步系统的动力学方程。
两小行星的自旋速度分别为ω1,ω2,初始的自旋角为θ1,θ2,则在质心旋转系下的自旋速度分别为ω′1=ω1-ω0,ω′2=ω2-ω0,自旋角随时间的变化为φ1=θ1+ω′1t,φ2=θ2+ω′2t,则动力学方程(1)变为,
其中Rz为绕Z轴的旋转矩阵。
步骤四、将步骤二得到的周期轨道族按照周期等分为若干段,取各段的初值带入式(6)进行积分,对轨道的速度进行修正,保证各段轨道的位置在非同步系统中保持连续。
记每段的初值为Xi=[xi,yi,zi,vxi,vyi,vzi],每段轨道的初始积分时间为其中T为轨道周期,n为分段数,可根据任意选取,增大n可以提高收敛性但降低计算速度。
微分修正方程:
其中δXi=[0,0,0,δvxi,δvyi,δvzi],δXi+1=[0,0,0,δvxi+1,δvyi+1,δvzi+1]
为初状态至末状态的状态转移矩阵。δvxi+1=vxi+1-vx′i+1,δyi+1=yi+1-y′i+1,δzi+1=zi+1-z′i+1。
Xi=[xi,yi,zi,vxi,vyi,vzi]按动力学方程(6)积分ti时间后的终值为X′i+1=[x′i+1,y′i+1,z′i+1,v′xi+1,v′yi+1,v′zi+1]。
式(8)可以表示为:
从而对每段初值进行修正,初值变为Xi+δXi。
对每一段轨道分别进行位置修正,得到新的初始速度,初始位置不变。
步骤五、对步骤四所述每段轨道的初始位置和积分时间进行修正,使各段的速度在非同步系统中保持连续。
对初值Xi=[xi,yi,zi,vxi,vyi,vzi]的速度修正同时取决于Xi-1=[xi-1,yi-1,zi-1,vxi-1,vyi-1,vzi-1]和Xi+1=[xi+1,yi+1,zi+1,vxi+1,vyi+1,vzi+1]的情况。
其中Vi=[vxi,vyi,vzi],Ri=[xi,yi,zi],Vi-表示从Xi-1正向积分得到的速度,而Vi+表示从Xi+1逆向积分得到的速度。
通过式(10)对每一段轨道进行速度修正,得到新的初始位置和每段积分时间。
步骤六、计算各段轨道间的位置和速度偏差,若小于某一值,则认为轨道连续,即得到稳定运行在非同步系统内的轨道,否则重复步骤四和五,直至满足约束。
记新修正的轨道各段位置误差和速度误差为δri和δvi,轨道总的位置误差记为总速度误差记为若δR<ε1且δV<ε2则认为轨道连续,即为稳定轨道,ε1,ε2为小量,优选为ε1=10-5m,ε2=10-3m/s,可以根据小行星的大小和任务精度调整。若不满足约束则重复步骤四和五,通过多次迭代得到稳定的轨道。
有益效果:
1、本发明公开的一种非同步双星系统的稳定轨道计算方法,首次得到在非同步双星系统中的稳定轨道,可用作探测任务的使命轨道。
2.本发明公开的一种非同步双星系统的稳定轨道计算方法,已同步双星系统计算得到的周期轨道作为初值,初值易获取。
2、本发明公开的一种非同步双星系统的稳定轨道计算方法,通过将轨道分段,分别进行位置修正和速度修正,提高了轨道的收敛性,轨道收敛性高。
附图说明
图1本发明的一种非同步双星系统的稳定轨道计算方法流程示意图;
图2同步双星系统下的周期轨道;
图3非同步双星系统旋转坐标系示意图;
图4分段轨道位置修正示意图;
图5分段轨道速度修正示意图;
图6本发明得到的非同步双星系统下的稳定轨道。
具体实施方式
为了更好的说明本发明的目的和优点,下面结合附图和实例对发明内容做进一步说明。
实施例1:
本实施例的一种非同步双星系统的稳定轨道计算方法,包括以下步骤:
步骤一、根据确定的目标双星系统参数,忽略自旋角速度差别,将双星系统考虑为同步双星系统,建立椭球-椭球双星系统模型,在质心旋转坐标系下建立动力学模型。所述的双星系统参数包括双星的形状、质量比和相对距离。
其中ρ表示探测器到质心的位置矢量,ω为系统的旋转角速度,ρ1和ρ2为探测器到双星主星和子星的位置矢量。U1,U2表示双星的引力势能:
其中α,β,γ为星体的三个主轴长度,r1,r2为两个星体在坐标系下的位置矢量。
设双星系统中主星的三轴长分别为0.6124km,0.6km,0.5880km;子星的三轴长分别为0.5530km,0.5364km,0.5300km,系统的质量常数μ=0.4083,轨道周期13.8936h,轨道角速度ω=1.2562×10-4rad/s。
步骤二、对同步双星系统进行周期轨道搜索,通过相应的搜索方法得到周期轨道族。
同步双星系统内的周期轨道满足利用双星系统模型的对称性能够对周期轨道的初始状态进行简化;对于面对称的轨道,轨道从OXZ平面出发,初值满足半个轨道周期后满足轴对称的轨道,轨道从X轴出发,初值满足半个轨道周期后应满足根据已有的搜索方法对双星系统内的区域进行搜索得到不同轨道周期和轨道能量的周期轨道族。
已有的搜索方法包括利用速度庞加莱映射或网格搜索。基于网格搜索得到的同步系统下的周期轨道如图2所示。
步骤三、根据双星系统的自旋速度,建立非同步系统的动力学方程。
取小行星的自旋周期分别为6.9468h和12.0545h,初始的自旋角均为θ1=0°,θ2=0°,则在质心旋转系下的自旋速度分别为ω′1=ω1-ω0=1.2562rad/s,ω′2=ω2-ω0=1.9167×10-5rad/s,则动力学方程(1)变为,
其中Rz为绕Z轴的旋转矩阵。
非同步双星系统在质心旋转系下的示意图如图3所示。
步骤四、将步骤二得到的周期轨道族按照周期等分为若干段,取各段的初值带入式(6)进行积分,对轨道的速度进行修正,保证各段轨道的位置在非同步系统中保持连续。
记每段的初值为Xi=[xi,yi,zi,vxi,vyi,vzi],每段轨道的初始积分时间为其中T为轨道周期,n为分段数,可根据任意选取,增大n可以提高收敛性但降低计算速度。
微分修正方程:
其中δXi=[0,0,0,δvxi,δvyi,δvzi],δXi+1=[0,0,0,δvxi+1,δvyi+1,δvzi+1]
为初状态至末状态的状态转移矩阵。δvxi+1=vxi+1-vx′i+1,δyi+1=yi+1-y′i+1,δzi+1=zi+1-z′i+1。
Xi=[xi,yi,zi,vxi,vyi,vzi]按动力学方程(6)积分ti时间后的终值为X′i+1=[x′i+1,y′i+1,z′i+1,v′xi+1,v′yi+1,v′zi+1]。
式(8)可以表示为:
从而对每段初值进行修正,初值变为Xi+δXi。
对每一段轨道分别进行位置修正,得到新的初始速度,初始位置不变,位置修正示意图如图4所示。
步骤五、对步骤四所述每段轨道的初始位置和积分时间进行修正,使各段的速度在非同步系统中保持连续。
对初值Xi=[xi,yi,zi,vxi,vyi,vzi]的速度修正同时取决于Xi-1=[xi-1,yi-1,zi-1,vxi-1,vyi-1,vzi-1]和Xi+1=[xi+1,yi+1,zi+1,vxi+1,vyi+1,vzi+1]的情况。
其中Vi=[vxi,vyi,vzi],Ri=[xi,yi,zi],Vi-表示从Xi-1正向积分得到的速度,而Vi+表示从Xi+1逆向积分得到的速度。
通过式(10)对每一段轨道进行速度修正,得到新的初始位置和每段积分时间,速度修正的示意图如图5所示。
步骤六、计算各段轨道间的位置和速度偏差,若小于某一值,则认为轨道连续,即得到稳定运行在非同步系统内的轨道,否则重复步骤四和五,直至满足约束。
记新修正的轨道各段位置误差和速度误差为δri和δvi,轨道总的位置误差记为总速度误差记为若δR<ε1且δV<ε2则认为轨道连续,即为稳定轨道,ε1,ε2为小量,优选为ε1=10-5m,ε2=10-3m/s,可以根据小行星的大小和任务精度调整。若不满足约束则重复步骤四和五,通过多次迭代得到稳定的轨道。经过多次迭代后得到的稳定轨道如图6所示。
以上所述的具体描述,对发明的目的、技术方案和有益效果进行了进一步详细说明,所应理解的是,以上所述仅为本发明的具体实施例而已,并不用于限定本发明的保护范围,凡在本发明的精神和原则之内,所做的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!