一种复杂腔体内部散射特性的计算方法与流程
本发明涉及雷达目标特性仿真技术,特别涉及一种复杂腔体内部散射特性的计算方法。
背景技术:
对腔体电磁散射特性的分析是飞行器隐身设计以及目标特征分析技术的重要基础,有着重要的现实意义,一直是计算电磁学的一个热点。腔体存在强烈的近谐振现象,由电磁场积分方程得到的矩阵往往具有较大的条件数,在迭代求解时收敛速度很慢,而且电大腔体属于电大问题。低频数值方法因为剖分密度大、未知量多,受到计算机内存和计算时间的限制难以用这些方法求解真实尺寸腔体的散射特性。基于几何光学的射线方法求解腔体具有实现简单、求解速度快等优点,但是求解精度不高、难以求解处理形状复杂的腔体。
南京理工大学在专利“基于矩量法和抛物线方程的含腔目标电磁散射分析方法”(公开号:CN104778151A)中,将目标中腔体部分单独用快速多极子进行求解,运用电场积分方程求解出腔体表面的电流,并求出腔体开口面上抛物线方程所需各个离散点的电场场值,对最后一个切面上的电场进行后处理求解雷达散射截面;南京理工大学在专利“腔体含介质目标电磁散射混合分析方法”(公开号:CN104915324A)中,将体面积分方程与无网格抛物线方程相结合,避免了抛物线不能计算腔体散射的缺陷;西北工业大学在专利“一种航空发动机喷管腔体电磁散射测试装置及测试方法”(公开号:CN105021899A)中,电磁散射测试装置采用在装置本体外壁面上包覆尖锥型吸波材料进行喷管腔体的电磁散射测试,外壁面的尖锥吸波材料可吸收大部分的雷达波,电磁测试中有效地屏蔽喷管模型外壁面的电磁波反射。
上述专利,南京理工大学在仿真上对含腔目标中的腔体做特殊处理,求解出来的雷达散射截面是含腔目标的总体效应;西北工业大学在测试方法上使用尖锥型吸波材料包覆喷管腔体,屏蔽喷管模型外壁面的电磁波反射,测试能够准确地反映喷管腔体的电磁散射特性。两者没有从仿真角度说明求解腔体内部散射特性的方法,若将后者测试用的方法直接应用到仿真上,会急剧增加计算未知量,无法切实开展电大尺寸腔体特性的计算。
技术实现要素:
本发明的目的是提供一种复杂腔体内部散射特性的计算方法,通过口径场激励代替低散射载体一方面减小了计算的未知量,同时也省去了低散射载体的设计。
为了实现以上目的,本发明是通过以下技术方案实现的:
一种复杂腔体内部散射特性的计算方法,其特点是,该计算方法包含如下步骤:
S1,根据腔体外形构建腔体的虚拟口径面;
S2,对激励源进行辐射积分,得出所述虚拟口径面的电磁场分布;
S3,将虚拟口径面上的电磁场分布作为激励源对整体腔体进行电磁计算,并构造采用线性方程组,求解腔体内部散射;
S4,采用Krylov子空间迭代法求解线性方程组;
S5,获得稳定的腔体内壁电流,并得到口径场,以所述的口径场作为激励源求解远场散射特性。
所述的步骤S1中虚拟口径面与腔体形成一闭合体。
所述的步骤S2之前包含将所述的虚拟口径面离散化这一步骤。
所述的步骤S2中采用公式(1)(2)对激励源进行辐射积分,
式中,Εi(ra)和Hi(ra)分别表示虚拟口径面ra处的电场和磁场,R表示源点到场点的单位径矢,J和M分别表示电流源和磁流源分布,k表示自由空间的波数,Z0表示自由空间的波阻抗。
所述的步骤S3具体包含:
步骤S3.1,将虚拟口径面上的电磁场分布作为激励源对整体腔体进行电磁场计算;
步骤S3.2,离散化腔体并根据所述的虚拟口径面上的电磁场,求解腔体内壁的电磁场,进而构造线性方程组,求解腔体内部散射。
所述的步骤S4具体为:对整个腔体作分段处理,采用Krylov子空间迭代法求解每段腔体的线性方程组。
所述的步骤5中采用公式(1)(2)求解口径场,且所述求解远场散射特性即为腔体内部散射特性。
本发明与现有技术相比,具有以下优点:
1、通过口径场激励代替低散射载体一方面减小了计算的未知量,同时也省去了低散射载体的设计。
2、通过两次使用惠更斯原理,以及在合理近似口径入射场的前提下,采用Krylov子空间迭代法高效求解大型线性方程组,获取腔体内部散射特性。
附图说明
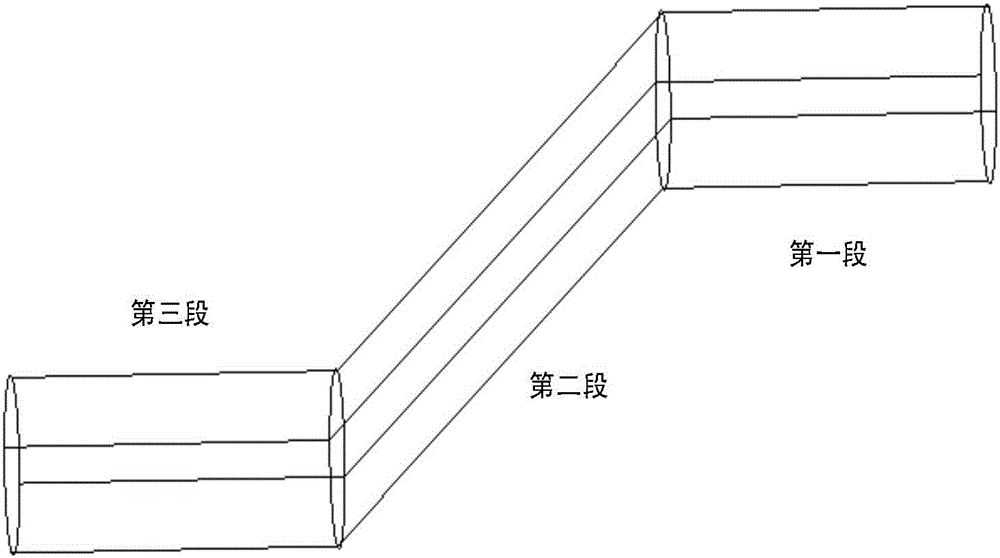
图1为本发明对腔体分段处理的结构示意图;
图2为本发明腔体及其虚拟口径面的结构示意图;
图3为整体照射腔体表面电流分布图;
图4为口径照射Cobra腔体表面电流分布图;
图5为对虚拟口径面离散化后的结构示意图;
图6为本发明一种复杂腔体内部散射特性的计算方法的流程图。
具体实施方式
以下结合附图,通过详细说明一个较佳的具体实施例,对本发明做进一步阐述。
如图6所示,一种复杂腔体内部散射特性的计算方法,该计算方法包含如下步骤:
S1,根据腔体外形构建腔体的虚拟口径面,一般要求虚拟口径面相对规则、平整,有利于求解其上的电磁场分布;
S2,对激励源进行辐射积分,得出所述虚拟口径面的电磁场分布;
S3,将虚拟口径面上的电磁场分布作为激励源对整体腔体进行电磁计算,并构造采用线性方程组,求解腔体内部散射;
S4,采用Krylov子空间迭代法求解线性方程组;
S5,获得稳定的腔体内壁电流,并得到口径场,以所述的口径场作为激励源求解远场散射特性。
所述的步骤S1中虚拟口径面与腔体形成一闭合体(参见图2)。
上述的步骤S2之前包含将所述的虚拟口径面离散化这一步骤(如图5)。
上述的步骤S2中采用公式(1)(2)对激励源进行辐射积分,
式中,Εi(ra)和Hi(ra)分别表示虚拟口径面ra处的电场和磁场,R表示源点到场点的单位径矢,J和M分别表示电流源和磁流源分布,k表示自由空间的波数,Z0表示自由空间的波阻抗;在求解出虚拟口径面上的电磁场分布之前,需要对公式(1)(2)进行离散化,一般采用RWG基函数将目标表面等效电磁流离散展开。
图3和图4分别是整体照射、口径照射时腔体表面电流分布。可以看出,整体照射时,直接照射到的腔体底部电流比口径激励时要高10dB以上。
上述的步骤S3具体包含:
步骤S3.1,将虚拟口径面上的电磁场分布作为激励源对整体腔体进行电磁场计算;
步骤S3.2,离散化腔体并根据所述的虚拟口径面上的电磁场,求解腔体内壁的电磁场,进而构造线性方程组,求解腔体内部散射。
上述的步骤S4具体为:(参见图1)对整个腔体作分段处理,采用Krylov子空间迭代法求解每段腔体的线性方程组,分段求解在改善矩阵条件数的前提下,缩小外迭代后期的Krylov子空间,大大降低所需迭代次数。
Krylov子空间方法是投影方法中的一种,它已经被广泛的使用在计算科学的各个领域。在大型线性系统的迭代求解中有着尤其重要的地位。有别于经典迭代法的求解思路,Krylov子空间方法在Krylov子空间中寻找线性系统的近似解,别开生面地提出了另外一种求解线性系统的方法。
腔体存在强烈的近谐振现象,由电磁场积分方程得到的矩阵往往具有较大的条件数,在迭代求解时收敛速度很慢。经典迭代法对于腔体散射问题的求解常常难以收敛、甚至趋于发散,Krylov子空间迭代法(广义共轭残差,GCR)能够克服大型稀疏线性方程不能收敛以及收敛速度缓慢的问题。
分段求解在改善矩阵条件数的前提下,能够更加充分地利用广义共轭残差迭代求解的优势。缩小外迭代后期的Krylov子空间,大大降低所需迭代次数。对于电大尺寸复杂腔体内部电磁散射求解可以获得稳定可靠的数值解。
所述的步骤5中采用公式(1)(2)求解口径场,且所述求解远场散射特性即为腔体内部散射特性。
综上所述,本发明一种复杂腔体内部散射特性的计算方法,通过口径场激励代替低散射载体一方面减小了计算的未知量,同时也省去了低散射载体的设计。
尽管本发明的内容已经通过上述优选实施例作了详细介绍,但应当认识到上述的描述不应被认为是对本发明的限制。在本领域技术人员阅读了上述内容后,对于本发明的多种修改和替代都将是显而易见的。因此,本发明的保护范围应由所附的权利要求来限定。
- 还没有人留言评论。精彩留言会获得点赞!