一种直线电机传递函数的迭代滤波辨识方法与流程

本发明涉及一种直线电机传递函数的迭代滤波辨识方法，属于直线电机控制技术领域。

背景技术：

目前，无论是在日常用品还是工业现场中都大量应用了运动控制系统，要使电机运行更平稳，更加可靠就要知道这个系统的精确模型参数。目前建立在CARMA模型(带控制量的自回归滑动平均模型)的辨识方法大都将滤波和辨识分开进行，且滤波器的参数都是定值，这就导致了辨识算法的不够灵活，适应性差，对实际应用过程中存在的环境干扰和测量噪声不能很好的过滤，进而影响辨识参数的准确性。

传递函数一般通过最小二乘法进行求解，最小二乘法通过最小化误差的平方来寻求数据的最佳匹配函数，并使得这些求得的数据与实际数据之间的平方和为最小，但是没有合适的滤波器辨识结果会导致求解出直线电机传递函数有较大的误差，影响直线电机的控制精度。

针对目前现有技术中存在的上述缺陷，实有必要进行研发，解决现有技术中存在的缺陷。

技术实现要素：

针对现有技术的缺陷，本发明的目的在于提供一种滤波辨识方法，避免了滤波器选择的难题和最小二乘算法抗干扰能力差的不足，提供了一种能够迭代学习滤波器的批处理最小二乘辨识方法，抗干扰能力强，参数辨识精度高，有助于实现对系统的高速高精控制的直线电机传递函数的迭代滤波辨识方法。

为实现上述目的，本发明的技术方案为：

一种直线电机传递函数的迭代滤波辨识方法，包括以下步骤：

第一步：连接好直线电机与运动控制卡，打开上位机软件，设置激励信号为白噪声，运动参数设置完成后下发给运动控制卡上，使得电机按照预设运动；同时运动控制卡开始采集激励信号和输出信号，并保存数据；

第二步：确定待辨识电机模型的系统阶次；

第三步：把已确定阶次的模型通过双线性变换公式将模型由s域转化为z域公式的形式；

所述模型为：

所述双线性变换公式为：

所述z域公式为：

其中G(s)为传递函数，Y(s)、U(s)分别为输出量和输入量的拉普拉斯变换；T为采样周期，z为延迟算子，α₀…α_n-1为离散化后传递函数的分子需要辨识的系数，β₁…β_n为离散化后传递函数的分母需要辨识的系数；

第四步：由β₁…β_n组成滤波器，第一次对输入输出数据进行滤波时设置

第五步：输入输出数据x、w经滤波器滤波后的数据为

第六步：由组成向量q’_j，由α₀…α_n-1，β₁…β_n组成向量δ；

δ’＝[α₀…，α_n-1，β₁…，β_n-1] (5)

其中q’_j、δ’为向量，是q_j、δ_j的转置，维数由待辨识系统的阶次来确定；

第七步：由公式(6)计算出矩阵Q；

Q＝∑q_jq’_j (6)

第八步：由公式(7)计算出向量C；

第九步：有公式(8)计算出含有待辨识参数α₀…α_n-1，β₁…β_n的向量δ；其中Q^-1表示对矩阵Q求逆；

δ＝Q^-1C (8)

第十步：从第四步开始重复迭代更新滤波器，直到辨识结果达到收敛要求，辨识完成，根据辨识结果设置控制器，使得直线电机高速平稳运行。

进一步地，开始辨识之前首先对输入输出数据用第四步的滤波器进行滤波；滤波器的分子系数为1，分母系数初始值为1，之后每次迭代更新上一次辨识结果的作为分母系数。

进一步地，第六步由滤波后的输入输出数据按照阶次的高低顺序排列组成列向量q’_j。

进一步地，第七步，矩阵Q为方阵，维数与待辨识参数个数相等。

进一步地，第八步，由公式(7)计算向量C；C的维数与待辨识参数个数相同。

进一步地，第九步，向量δ中的α₀…α_n-1，β₁…β_n按照系数阶次的高低顺序排列。

与现有技术相比，本发明具有以下有益效果：

本发明在批处理最小二乘辨识算法里面融合了迭代学习滤波器，能够根据待辨识系统的特点来生成对应的滤波器，减少了需要专门设计滤波器的工作，此外本发明由于加入了滤波算法，辨识出的数据更加精确，有利于高精度控制器的设计。本发明对参数辨识及控制系统的设计，无疑具有一定的现实意义和实用价值。

本发明抗干扰能力强，参数辨识精度高，有助于实现对系统的高速高精控制，避免了滤波器选择的难题和最小二乘算法抗干扰能力差的不足。

附图说明

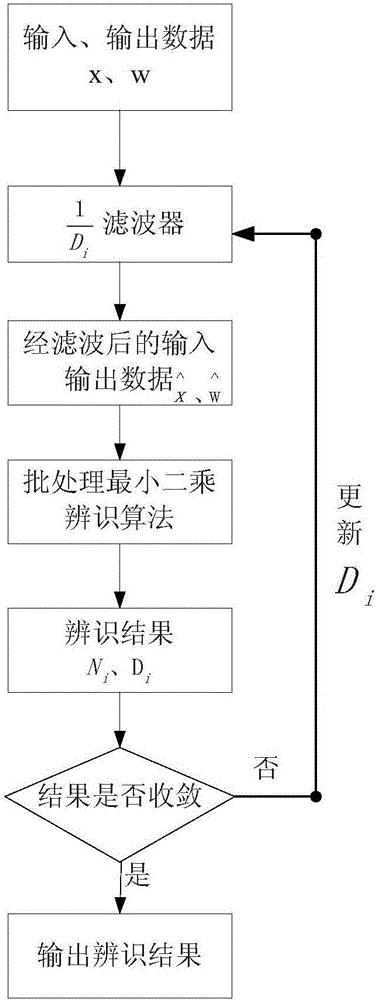
图1是本发明流程图；

图2是最小二乘辨识拟合结果；

图3是本发明的迭代滤波辨识拟合结果。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

相反，本发明涵盖任何由权利要求定义的在本发明的精髓和范围上做的替代、修改、等效方法以及方案。进一步，为了使公众对本发明有更好的了解，在下文对本发明的细节描述中，详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。

如图1所示，一种直线电机传递函数的迭代滤波辨识方法，包括以下步骤：

第一步：连接好直线电机与运动控制卡，打开上位机软件，设置激励信号为白噪声，运动参数设置完成后下发给运动控制卡上的DSP芯片，使得电机按照预设运动。同时运动控制卡开始采集激励信号和输出信号，并保存数据。

第二步：确定待辨识系统模型的阶次。

第三步：把已确定阶次的模型(1)通过双线性变换公式(2)将模型由s域转化为z域公式(3)的形式。

其中G(s)为传递函数，Y(s)、U(s)分别为输出量和输入量的拉普拉斯变换。T为采样周期，z为延迟算子，α₀…α_n-1为离散化传递函数的分子需要辨识的系数，β₁…β_n为离散化传递函数的分母需要辨识的系数。

第四步：由β₁…β_n组成滤波器，第一次对输入输出数据进行滤波时设置

开始辨识之前首先对输入输出数据用滤波器进行滤波，滤波器的分子系数为1，分母系数初始值为1，之后每次迭代更新上一次辨识结果的β₁…β_n作为分母系数。

第五步：输入输出数据x、w经滤波器滤波后的数据为

第六步：由组成向量q’_j，滤波后的输入输出数据按照阶次的高低顺序排列组成列向量q’_j。由α₀…α_n-1，β₁…β_n组成向量δ’。

其中q’_j、δ’为向量，是q_j、δ_j的转置，维数由待辨识系统的阶次来确定。

第七步：由公式(6)计算出矩阵Q，矩阵为方阵，维数与待辨识参数个数相等。

Q＝∑q_jq’_j (6)

第八步：由公式(7)计算出向量C，C的维数与待辨识参数个数相同。

第九步：有公式(8)计算出含有待辨识参数α₀…α_n-1，β₁…β_n的向量δ。其中Q^-1表示对矩阵Q求逆，向量δ中的α₀…α_n-1，β₁…β_n按照系数阶次的高低顺序排列。

δ＝Q^-1C (8)

第十步：从第三步开始重复迭代更新滤波器，直到辨识参数达到收敛要求，输出辨识结果。辨识完成。

如图2-3所示，把本发明运用到直线电机上，可以显著辨识出传递函数的振荡环节，针对震动环节设计控制器，控制直线电机高速平稳的运行。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。