一种从单一二维掌纹图像恢复三维特征的掌纹识别方法与流程

本发明涉及掌纹识别领域，尤其是涉及了一种从单一二维掌纹图像恢复三维特征的掌纹识别方法。

背景技术：

从二维图像恢复三维信息在许多领域有广泛的应用，例如罪犯监控，三维打印，三维建模以及远程掌纹诊断等。高效和精确的特征描述符的设计和开发是许多计算机视觉应用程序成功的关键。在过去的方法中，由于光线的影响，掌纹识别过程变得较为困难，而且需要多张二维图像才能获得3维特征信息，所占存储也比较大，匹配效果不佳，实用性不强。

针对以上问题，本发明基于序数测度的新特征，从单一的二维掌纹图像中提取3D信息，还提供了用于掌纹匹配的序度量的有效性分析。特征描述符(DN)描述了三维信息，在非接触成像过程中对于发生的光照变化是高度稳定的；而且DN每个点的大小只有一位，提取简单，易于匹配，并有效地存储。本发明特征提取和匹配效果好，实现简单，实用性强。它具有较低的存储需求，同时能有效地恢复/提取和匹配，性能准确；从单一二维掌纹图像恢复三维形状信息，也意味着冗余更少。

技术实现要素：

针对光线的影响大，所占存储也比较大，匹配效果不佳，实用性不强等问题，本发明的目的在于提供一种从单一二维掌纹图像恢复三维特征的掌纹识别方法，基于序数测度的新特征，从单一的二维掌纹图像中提取3D信息，还提供了用于掌纹匹配的序度量的有效性分析。特征提取和匹配效果好，实现简单，实用性强。

为解决上述问题，本发明提供一种从单一二维掌纹图像恢复三维特征的掌纹识别方法，其主要内容包括：

(一)从单一的2D图像获得3D特征；

(二)区域划分；

(三)模板去噪与匹配；

(四)掌纹匹配分析。

其中，所述的一种从单一二维掌纹图像恢复三维特征的掌纹识别方法，其特征在于，基于序数测度的新特征，从单一的二维掌纹图像中提取3D信息，还提供了用于掌纹匹配的序度量的有效性分析；特征提取和匹配效果好，简单实现，实用性强。

其中，所述的从单一的2D图像获得3D特征，利用顶点法线向量差异(DN)特征描述 顶点法线向量差异和引入朗勃模型。

进一步地，所述的利用顶点法线向量差异(DN)特征描述了顶点法线向量差异，其特征在于，方法如下：

为了更好地描述特征，为每个图片建立笛卡尔坐标直角坐标系，图像平面形成x-y平面，图片的代表z轴；

平面图像上的每个点/像素P_i一一对应到物体的表面顶点v_i；使n_i＝(x_i,y_i,z_i)，代表定点法线向量v_i；假设点P_i有2个邻近区域，和则它的DN特征DN(i)为

其中τ(·)是符号函数，定义为

P_i的DN特征描述了z轴法向向量邻近区域的差异，根据公式(1)，恢复点P_i的DN特征的两个关键问题为：

(1)从它的临近区域获得z值；

(2)确定点的临近区域。

进一步地，所述的引入朗勃模型，其特征在于，根据朗勃模型，图像上的点P_i的像素值I(i)是由反射比k_d，光照强度l_d和光照方向向量L和点的法向量n_i决定的，

I(i)＝k_dl_dLn_i (3)

根据相同图像上的不同的点，可认为他们的k_d,l_d,L是相同的；

给定一个点P_i，临近区域和的点强度的差异为用符号函数τ代表这两个部分，定义D(i)为

使用公式(3)，(4)，可以重写为

D(i)是由光照矢量L与矢量之间的夹角确定的；

为了简便，使

使L＝(a,b,c)，有

D(i)＝τ(ΔX_ia+ΔY_ib+ΔZ_ic) (7)

掌纹图像总是在正面照明下获得的；

因此，在上述的直角坐标系下，有c>0，当满足D(i)是由ΔZ_i标志决定的，例如

τ(ΔZ_i)代表准备恢复的DN特征DN(i)；公式(8)证明了三维信息DN(i)可以从单一的二维图像恢复；当约束满足可利用现有的纹理信息恢复三维形状信息；

对于样品|ΔX_ia|>|ΔY_ib|的情况下，约束可以重写为

是由不可控的成像过程中的光照所决定的；为了满足公式(9)的约束条件，确保右边的 尽可能小；

通过由一个符号函数使用卷积运算，使用DN进行特征提取；在掌纹图像上的相邻区域的分区，替换空间滤波器上的区域的划分；在一个尺寸为M×N的空间频率滤波器中，对应的操作过滤器的空间区域被分为两个亚群，命名为R₁和R₂；在区域R₁的所有条目设置为1，在区域R₂的所有条目设置为-1；扩展τ到矩阵运算，DN特征矩阵或图像I的模板F计算如下：

F＝τ(f*I) (10)

公式(10)是一个计算更简单的操作，用于从单一的二维图像恢复为三维信息。

进一步地，所述的特征描述符(DN)，其特征在于，对二维掌纹进行匹配，提取的描述符上的每个点上的掌纹；它是基于序数测度，部分地描述了相邻点的正规向量的差异，优点在于：

(1)它描述了三维信息，在非接触成像过程中对于发生的光照变化是高度稳定的；

(2)DN每个点的大小只有一位，提取简单，易于匹配，并有效地存储。

其中，所述的区域划分，通过分区上的空间滤波器的局部区域确定临近地区；考虑到二值特征模板产生的(非接触式成像)图像，在过滤器中的所有条目的总和应该是零；过滤器中的1或-1的空间分布是对称有序的；

划分应确保在公式(9)的约束的右侧是尽可能小的，即令ΔX_i近似为零，ΔZ_i是一个很大的值

如果相邻区域划分被设计为连续连接和补丁，预计因此它们的区别ΔX_i≈0，有两个原因：

(1)对称单元在X-Y平面，这样的划分确保区域表面的对称性；当点的法线向量被添加时，方位分量有很大的机会几乎被取消或消除；

(2)X-Y平面几乎是一个平面，这表明大多数点分量为零；

ΔZ_i的值很大有两个原因：

(1)因为每个z_i都为正值，所以本身是个很大的值，这主要由大小和山谷的长度决定；

(2)由于掌纹表面上的山谷单元的不规则分布，和也不同；

因此，掌纹图像更可能有小的值，满足公式(9)的约束。

进一步地，所述的过滤器，可定义如下：

其中i,j是指数，i,j∈[-B,B]；过滤器的大小是(2B+1)×(2B+1)。

其中，所述的模板去噪与匹配，采用匹配过程中的去噪策略；

给定两个特征模板F₁和F₂，匹配的距离计算的加权总和的三个分数，

其中和应用功能模板F上的关闭和打开操作后的结果；

S(F₁,F₂)定义为

其中和&是XOR和AND操作，Γ(F)计算矩阵F中的非零值的数目，M(I)是表示掌纹 图像I上有效区域的掩码矩阵，定义为

使用水平和垂直的两个匹配的模板之间的转换，以提高准确性；在所有的实验中，这些路线中最好的匹配得分作为最终的匹配得分。

其中，所述的掌纹匹配分析，特征或模板的掌纹图像通常是一个特征矩阵；在矩阵中的每个条目都是一个编码的特征码；两个模板之间的距离被定义为代码之间的距离的总和；模板距离是通常用来测量码的距离，代码通常是二进制；

如果这两个掌纹图像属于同一类，称之为类内匹配距离或真正的匹配距离；若属于不同类，称之为类间距离的匹配；为了简化分析，如果两个代码之间的距离是相等的，则被假定为零；对于一个128×128掌纹模版，它的特征向量的维数是16384；考虑到掌纹区域的空间依赖性，假定单一的掌纹特征向量的内在尺寸，用M表示M为1000；

考虑到类间的匹配尝试，无论是匹配或不匹配的模板上的代码可以被视为一个随机事件；这是因为两个掌纹来自不同类，而且是未知的；因此，假定级间匹配距离D_inter的分布依照二项式分布如下

D_inter～B(n_inter,p) (15)

n_inter是二项分布的试验数量，和M相同，p是成功概率，λ和p的关系为

对于一个可靠的代码对，匹配的距离应该肯定是零；对于一个不可靠的对，匹配距离仍可能为零；因此，有效地确定了两个模板之间的类内匹配距离由不可靠的代码对的数量；对于不可靠的对，无论这些代码是否匹配也可以被视为一个随机事件；这是因为不可靠的代码主要是由噪声和不重合造成，其确切影响未知；表示不可靠对的数目ωM，其中ω是不可靠的对率(0＜ω＜1)，假设类内匹配距离D_intra如下的二项分布：

D_intra～B(n_intra,p) (17)

n_intra是数量的试验，这是等于不可靠的对数ωM，p是成功率；p和λ的关系是相同的类间距离分布；

一个不可靠的对产生的可能性可以估计为

θ＝1-(1-p)(1-p) (18)

V代表不可靠的代码对的预期率；因此，假设V与U成正比是合理的，

ω∝θ (19)

给出两个λ，

上式为p₁，p₂，ω₁，ω₂的对应关系。

附图说明

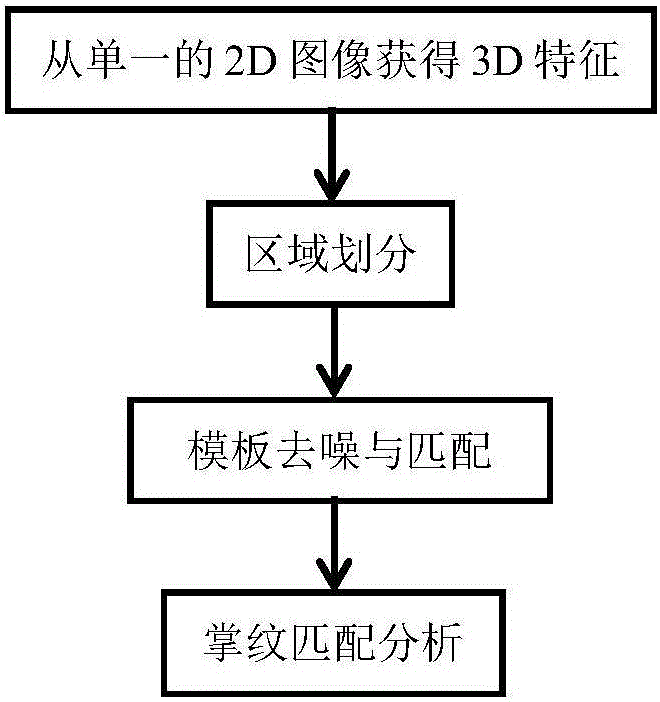
图1是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的系统流程图。

图2是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的一个典型的掌纹图像及其编码特征。

图3是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的二维图像上掌纹表面的投影。

图4是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的一个典型的掌纹线的点上的法线向量的求和结果。

图5是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的不同种类的候选滤波器。

具体实施方式

需要说明的是，在不冲突的情况下，本申请中的实施例及实施例中的特征可以相互结合，下面结合附图和具体实施例对本发明作进一步详细说明。

图1是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的系统流程图。主要包括从单一的2D图像获得3D特征、区域划分、模板去噪与匹配、掌纹匹配分析。

其中，从单一的2D图像获得3D特征，利用顶点法线向量差异(DN)特征描述顶点法线向量差异和引入朗勃模型。

利用顶点法线向量差异(DN)特征描述了顶点法线向量差异，其特征在于，方法如下：

为了更好地描述特征，为每个图片建立笛卡尔坐标直角坐标系，图像平面形成x-y平面，图片的代表z轴；

平面图像上的每个点/像素P_i一一对应到物体的表面顶点v_i；使n_i＝(x_i,y_i,z_i)，代表定点法线向量v_i；假设点P_i有2个邻近区域，和则它的DN特征DN(i)为

其中τ(·)是符号函数，定义为

P_i的DN特征描述了z轴法向向量邻近区域的差异，根据公式(1)，恢复点P_i的DN特征的两个关键问题为：

(1)从它的临近区域获得z值；

(2)确定点的临近区域。

引入朗勃模型，是根据朗勃模型，图像上的点P_i的像素值I(i)是由反射比k_d，光照强度l_d和光照方向向量L和点的法向量n_i决定的，

I(i)＝k_dl_dLn_i (3)

根据相同图像上的不同的点，可认为他们的k_d,l_d,L是相同的；

给定一个点P_i，临近区域和的点强度的差异为用符号函数τ代表这两个部分，定义D(i)为

使用公式(3)，(4)，可以重写为

D(i)是由光照矢量L与矢量之间的夹角确定的；

为了简便，使

使L＝(a,b,c)，有

D(i)＝τ(ΔX_ia+ΔY_ib+ΔZ_ic) (7)

掌纹图像总是在正面照明下获得的；

因此，在上述的直角坐标系下，有c>0，当满足D(i)是由ΔZ_i标志决定的，例如

τ(ΔZ_i)代表准备恢复的DN特征DN(i)；公式(8)证明了三维信息DN(i)可以从单一的二维图像恢复；当约束满足可利用现有的纹理信息恢复三维形状信息；

对于样品|ΔX_ia|>|ΔY_ib|的情况下，约束可以重写为

是由不可控的成像过程中的光照所决定的；为了满足公式(9)的约束条件，确保右边的 尽可能小；

通过由一个符号函数使用卷积运算，使用DN进行特征提取；在掌纹图像上的相邻区域的分区，替换空间滤波器上的区域的划分；在一个尺寸为M×N的空间频率滤波器中，对应的操作过滤器的空间区域被分为两个亚群，命名为R₁和R₂；在区域R₁的所有条目设置为1，在区域R₂的所有条目设置为-1；扩展τ到矩阵运算，DN特征矩阵或图像I的模板F计算如下：

F＝τ(f*I) (10)

公式(10)是一个计算更简单的操作，用于从单一的二维图像恢复为三维信息。

其中，区域划分，是通过分区上的空间滤波器的局部区域确定临近地区；考虑到二值特征模板产生的(非接触式成像)图像，在过滤器中的所有条目的总和应该是零；过滤器中的1或-1的空间分布是对称有序的；

划分应确保在公式(9)的约束的右侧是尽可能小的，即令ΔX_i近似为零，ΔZ_i是一个很大的值

如果相邻区域划分被设计为连续连接和补丁，预计因此它们的区别ΔX_i≈0，有两个原因：

(1)对称单元在X-Y平面，这样的划分确保区域表面的对称性；当点的法线向量被添加时，方位分量有很大的机会几乎被取消或消除；

(2)X-Y平面几乎是一个平面，这表明大多数点分量为零；

ΔZ_i的值很大有两个原因：

(1)因为每个z_i都为正值，所以本身是个很大的值，这主要由大小和山谷的长度 决定；

(2)由于掌纹表面上的山谷单元的不规则分布，和也不同；

因此，掌纹图像更可能有小的值，满足公式(9)的约束。

过滤器可定义如下：

其中i,j是指数，i,j∈[-B,B]；过滤器的大小是(2B+1)×(2B+1)。

其中，模板去噪与匹配，采用匹配过程中的去噪策略；

给定两个特征模板F₁和F₂，匹配的距离计算的加权总和的三个分数，

其中和应用功能模板F上的关闭和打开操作后的结果；

S(F₁,F₂)定义为

其中和&是XOR和AND操作，Γ(F)计算矩阵F中的非零值的数目，M(I)是表示掌纹图像I上有效区域的掩码矩阵，定义为

使用水平和垂直的两个匹配的模板之间的转换，以提高准确性；在所有的实验中，这些路线中最好的匹配得分作为最终的匹配得分。

其中，掌纹匹配分析，特征或模板的掌纹图像通常是一个特征矩阵；在矩阵中的每个条目都是一个编码的特征码；两个模板之间的距离被定义为代码之间的距离的总和；模板距离是通常用来测量码的距离，代码通常是二进制；

如果这两个掌纹图像属于同一类，称之为类内匹配距离或真正的匹配距离；若属于不同类，称之为类间距离的匹配；为了简化分析，如果两个代码之间的距离是相等的，则被假定为零；对于一个128×128掌纹模版，它的特征向量的维数是16384；考虑到掌纹区域的空间依赖性，假定单一的掌纹特征向量的内在尺寸，用M表示M为1000；

考虑到类间的匹配尝试，无论是匹配或不匹配的模板上的代码可以被视为一个随机事件；这是因为两个掌纹来自不同类，而且是未知的；因此，假定级间匹配距离D_inter的分布依照二项式分布如下

D_inter～B(n_inter,p) (15)

n_inter是二项分布的试验数量，和M相同，p是成功概率，λ和p的关系为

对于一个可靠的代码对，匹配的距离应该肯定是零；对于一个不可靠的对，匹配距离仍可能为零；因此，有效地确定了两个模板之间的类内匹配距离由不可靠的代码对的数量；对于不可靠的对，无论这些代码是否匹配也可以被视为一个随机事件；这是因为不可靠的代码主要是由噪声和不重合造成，其确切影响未知；表示不可靠对的数目ωM，其中ω是不可靠的对率(0＜ω＜1)，假设类内匹配距离D_intra如下的二项分布：

D_intra～B(n_intra,p) (17)

n_intra是数量的试验，这是等于不可靠的对数ωM，p是成功率；p和λ的关系是相同的类间距离分布；

一个不可靠的对产生的可能性可以估计为

θ＝1-(1-p)(1-p) (18)

V代表不可靠的代码对的预期率；因此，假设V与U成正比是合理的，

ω∝θ (19)

给出两个λ，

上式为p₁，p₂，ω₁，ω₂的对应关系。

图2是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的一个典型的掌纹图像及其编码特征。从单一的2D图像获得3D特征，利用顶点法线向量差异(DN)特征描述顶点法线向量差异和引入朗勃模型。

图3是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的二维图像上掌纹表面的投影。为了更好地描述特征，为每个图片建立笛卡尔坐标直角坐标系，图像平面形成x-y平面，图片的代表z轴；

平面图像上的每个点/像素P_i一一对应到物体的表面顶点v_i；使n_i＝(x_i,y_i,z_i)，代表定点法线向量v_i；假设点P_i有2个邻近区域，和则它的DN特征DN(i)为

其中τ(·)是符号函数，定义为

P_i的DN特征描述了z轴法向向量邻近区域的差异，根据公式(1)，恢复点P_i的DN特征的两个关键问题为：

(1)从它的临近区域获得z值；

(2)确定点的临近区域。

图4是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的一个典型的掌纹线的点上的法线向量的求和结果。通过分区上的空间滤波器的局部区域确定临近地区；考虑到二值特征模板产生的(非接触式成像)图像，在过滤器中的所有条目的总和应该是零；过滤器中的1或-1的空间分布是对称有序的；

划分应确保在公式(9)的约束的右侧是尽可能小的，即令ΔX_i近似为零，ΔZ_i是一个很大的值

如果相邻区域划分被设计为连续连接和补丁，预计因此它们的区别ΔX_i≈0，有两个原因：

(1)对称单元在X-Y平面，这样的划分确保区域表面的对称性；当点的法线向量被添加时，方位分量有很大的机会几乎被取消或消除；

(2)X-Y平面几乎是一个平面，这表明大多数点分量为零；

ΔZ_i的值很大有两个原因：

(1)因为每个z_i都为正值，所以本身是个很大的值，这主要由大小和山谷的长度决定；

(2)由于掌纹表面上的山谷单元的不规则分布，和也不同；

因此，掌纹图像更可能有小的值，满足公式(9)的约束。

图5是本发明一种从单一二维掌纹图像恢复三维特征的掌纹识别方法的候选滤波器。选择图5(b)的过滤器来构造特征提取器或过滤器，可定义如下：

其中i,j是指数，i,j∈[-B,B]；过滤器的大小是(2B+1)×(2B+1)。

对于本领域技术人员，本发明不限制于上述实施例的细节，在不背离本发明的精神和范围的情况下，能够以其他具体形式实现本发明。此外，本领域的技术人员可以对本发明进行 各种改动和变型而不脱离本发明的精神和范围，这些改进和变型也应视为本发明的保护范围。因此，所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。