一种位置服务中识别关键路径的方法与流程

本发明涉及位置服务(LBS)和数据处理领域，尤其涉及一种位置服务中识别关键路径的方法。

背景技术：

随着卫星导航定位和移动互联网的迅速发展，特别是位置服务不断普及的今天，由地理数据、轨迹信息和应用记录等所构成的位置大数据已成为政府或企业用来感知人类社群活动规律、分析地理国情和构建智慧城市的重要战略性资源，是大数据实践中极其重要的一部分。与传统小样统计不同，大规模的位置数据存在明显的混杂性、冗余性和稀疏性，需要对其进行特征提取和价值挖掘，才能获得更为准确的移动行为模式和区域局部特征，从而还原和生成满足关联应用分析的整体数据模型，并为开展个性化、智能化的位置服务提供关键数据支撑。

位置服务平台在处理服务接入上，由于平台与目标是分离的，对平台而言不可能完全了解目标的意图，其往往是不限制时间、不限制距离、不限制流量的，由目标周期性自主地上报位置数据。在云计算日益完善的当下，分布式的大数据平台可以有效地实现这种高并发、海量的数据存储与服务。这种目标自主的服务接入方式使得平台可以尽可能多地掌握目标的位置信息。但是，周期性频繁上报的位置并不能完全贴合目标的行动意图，这就降低了数据的整体质量。另一方面，由于移动网络的可靠性和高费用等特点，使得平台对于服务接口的数据质量要求非常高。

发明目的

本发明的目的是提供一种位置服务中识别关键路径的方法，通过路径信息来推断目标的运动意图，通过预判算法来缩减运动轨迹的信息量并记录缩减数。

本发明一种位置服务中识别关键路径的方法，包括提供位置服务的统一接入与服务的云平台和存储有位置数据的位置库，定义关键路径为目标在某时间段内的关键位置点的集合，其描述的是目标在该时间段内的关键运动轨迹，该关键位置点为运动过程中产生关键特征的位置点，包括如下步骤：

步骤1、数据检索：从位置库中检索目标的全部轨迹信息或者是某一时间段内的轨迹信息，该位置库内包含了目标上行的所有位置信息，其中符合检索条件的位置数据集称之为元数据；

步骤2、坐标降维：将元数据的经纬度通过高斯-克吕格投影转换为平面坐标式；

步骤3、压缩率r计算：将元数据个数与预期的输出结果集个数进行比较可得到压缩率

其中，s为目标的平面数据集S的大小，m为预期的输出结果集M的大小，m是与应用环境相关的可变参数；ceil(o)表示大于或者等于0的最小整数；当时，则直接跳到步骤7返回元数据；

步骤4、通过跨点抽样的方式,计算轨迹的距离基准值:

步骤5、分组及跨区关键点识别：采用上述的距离基准值对轨迹位置点进行分组，并标识分组中时间最前的位置点为跨区关键点；

步骤6、组内关键路径的计算：计算位置点与该点前两个位置点的运动状态表达式，确定该位置点是否是与前两个位置点的运动状态同质，进而得到该分组的关键路径；

步骤7、结果合并与再分析：依照步骤6的方法得到所有分组的关键路径，将各分组的关键路径结果按时间前后合并，并分析输出结果集的数量与预期的输出结果集的比值，确定是否直接返回处理结果。

所述的通过上述的高斯-克吕格地图投影算法计算后，得到目标的平面数据集S，按目标的平面数据集S中位置点上报的时间依次编号为S₁、S₂、S₃…S_n，其中，S₁的X轴坐标值设为x₁，Y轴坐标值设为y₁；依次类推，则S_n的X轴坐标值为x_n，Y轴坐标为y_n，如此可知，其他位置点在S₁时间之后，称为S₁的后置点，其中S₂为S₁的紧后点；同样的，S₁称之为S₂的前置点，也是紧前点；定义动态数组M₁存放关键位置点信息，并作为最终的输出结果集，其中，数组元素Data的结构为：{Lon经度,Lat纬度,Date时间,…，Stat位置类型，Drill:缩减节点个数}，其中，Lon经度、Lat纬度、Date时间为位置点的原始信息；Stat为位置点的类型，其值包括0和1，分别代表跨区点和偏转点；Drill为该点与动态数组M₁中紧前点之间缩减的位置点个数；所述步骤4通过跨点抽样的方式,计算轨迹的距离基准值，包括如下步骤：

步骤4.1、根据目标的平面数据集S及所得压缩率r，在目标的平面数据集S中每隔r个点抽取一个点组成{S₁，S_1+r…S_1+(m-1)r}集合，并计算相邻两点的距离，距离计算的方法为：

其中，(x_i,y_i)为S_i的坐标，(x_i+1,y_i+1)为S_i+1的坐标；

步骤4.2、距离基准值的计算方法为：

其中，v表示计算压缩率r运行的次数，d_ir为步骤4.1中距离计算公式所得的S_i和S_i+r之间的距离，其中i∈[1,m]，j为预置参数，Δd表示距离基准值等于精确到百位的相邻抽样点的距离均值。

所述的分组及跨区关键点识别，具体包括如下步骤：

将平面坐标系的横纵坐标从坐标原点(0,0)开始，采用所述的距离基准值为正方形边长对平面进行分区，并用每个最小正方形中的最大横、纵坐标来标识该分区，同时标记每个位置数据所在的分区坐标，然后将时间连续且分区一致的位置点归并一组，并标识分组中时间最前的位置点为跨区关键点。

所述的组内关键路径计算，具体包括如下步骤：

分析组内位置点的个数，如果个数小于阈值，则将组内的位置点都视为关键位置点，并跳过本组的压缩直接进入下一组的组内分析；

依次判别分组内的所有位置点，计算位置点与该点前两个位置点的运动状态表达式，确定该位置点是否是与该点前两个位置点运动状态同质，由此确定下一位置点是过滤，还是将其标识为偏转位置点。

本发明的优点及积极效果在于：

(1)本发明是目标相关性的关键路径识别，将目标在一个时间段内的运动轨迹视为紧前状态的延伸，从中可以简化目标混杂的运动状态，识别运动状态中的关键位置点，并将其描述为目标在该时间段的关键运动轨迹；

(2)本发明方法在确定基准值时，其采样策略是目标运动状态相关的，是利用目标在某时间段的位移变化幅度求均差而得，其有效的吻合不同类型目标的场景，也即目标在高速运行过程中，距离基准取值较大，反之则取值较小，这样可以精准的控制关键点所处的区域，使得最终关键路径的描述与目标自身的运动轨迹高度一致；

(3)本发明方法在位置点状态识别时，不仅考虑了位置的移动因素，而且还将位置的方位变化考虑在内，创造性的设计了预判算法，实现了简化算法的简洁、高效、易于理解；

(4)本发明方法在位置服务的实际应用中，不仅从运行效率、准确率及压缩率都体现了前所未有的优势，使得分布式的位置服务平台能够精准、便捷、提供适合移动网络环境下的轨迹回放服务。

附图说明

图1为本发明实施例的整体逻辑流程图；

图2为本发明实施例的预判区示意图；

图3为本发明实施例的偏转基准线角度关系图；

图4为本发明实施例的平面坐标系内的两矢量的顺逆时针关系图；

图5为本发明实施例的数据抽取处理逻辑流程图。

以下结合附图和具体实施例对本发明作进一步详述。

具体实施方式

本实施例以RT-CLBS空间位置服务云平台中关键路径的识别为原型，详细描述本发明的实施方式。RT-CLBS空间位置服务云平台是一个开放性的公共服务平台，旨在提供位置服务的统一接入与服务，以下简称云平台，其中位置数据的存储组件称之为位置库。关键路径指目标在某时间段内的关键位置点的集合，其描述的是目标在该时间段内的关键运动轨迹，运动过程中产生诸如跨区、方位偏转等关键特征的位置点，我们称之为关键点。

如图1所示，本发明一种位置服务中识别关键路径的方法，包括提供位置服务的统一接入与服务的云平台和存储有位置数据的位置库，定义关键路径为目标在某时间段内的关键位置点的集合，其描述的是目标在该时间段内的关键运动轨迹，该关键位置点为运动过程中产生关键特征的位置点，具体包括如下步骤：

步骤1、数据检索：从位置库中检索目标的全部轨迹信息或者是某一时间段内的轨迹信息，该位置库内包含了目标上行的所有位置信息，其中符合检索条件的位置数据集称之为元数据；

步骤2、坐标降维：将检索到的元数据的经纬度数据通过高斯-克吕格投影转换为平面坐标式，即使用高斯-克吕格地图投影算法将经纬度数据向平面直角坐标系转换，生成降维源数据，其具体转换过程如下所述：

步骤2.1、依据高斯-克吕格地图投影从0度子午线起每隔6度经差，自西向东分为60个分带，将带号分别标记为1、2、3…60带；

步骤2.2、将这60个分带投影到横切于地球椭球体上的椭圆柱体，该椭圆柱体表面与椭球体表面的切线为一经线，称之为中央经线，然后根据投影条件，将中央经线两侧规定范围内的点投影到椭圆柱体表面上，从而得到可展开的平面直角坐标系，即高斯-克吕格地图投影；

高斯-克吕格投影具有以下特性：

(1)中央子经线和地球赤道投影为直线，且为投影的对称轴；

(2)椭球面上的任意角度投影到平面后保持不变；

(3)中央子午线投影后没有长度变形；

步骤2.3、上述分带及高斯-克吕格地图投影后，我国的带号范围在13～23之间，在平面直角坐标系，X轴的坐标都是由赤道起算的自然值，而由于中央经线以东取正号，以西取负号，为避免Y轴坐标出现负值，所以在纵坐标y取值上分别加上500KM，并在纵坐标之前冠以带号；

依据上述转换，地图上经纬度为{Lon:118°10′,Lat:24°29′}的位置点，经高斯-克吕格地图投影后，平面坐标为{X:2710562.99827803,Y:20619384.2129943}，其中Y值前两位“20”代表该点在第20投影带；

步骤2.4、通过上述的高斯-克吕格地图投影算法计算后，得到目标的平面数据集S，按目标的平面数据集S中位置点上报的时间依次编号为S₁、S₂、S₃…S_n，其中，S₁的X轴坐标值设为x₁，Y轴坐标值设为y₁；依次类推，则S_n的X轴坐标值为x_n，Y轴坐标为y_n，如此可知，其他位置点在S₁时间之后，称为S₁的后置点，其中S₂为S₁的紧后点；同样的，S₁称之为S₂的前置点，也是紧前点；

同时，定义动态数组M₁存放关键位置点信息，并作为最终的输出结果集，其中，数组元素Data的结构为：{Lon经度,Lat纬度,Date时间,…，Stat位置类型，Drill:缩减节点个数}

其中，Lon经度、Lat纬度、Date时间为位置点的原始信息；Stat为位置点的类型，其值包括0和1，分别代表跨区点和偏转点；Drill为该点与动态数组M₁中紧前点之间缩减的位置点个数；

步骤3、压缩率r计算：将元数据个数与预期的输出结果集个数进行比较可得到压缩率

其中，s为目标的平面数据集S的大小，m为预期的输出结果集M的大小，m是与应用环境相关的可变参数；ceil(o)表示大于或者等于0的最小整数；所述云平台为移动端提供时间段内的轨迹回放查询，根据实际场景的需求，设m＝20，根据上述公式可得r＝n/20，当时，则直接转至步骤7返回元数据，并不做逻辑处理；

步骤4、通过跨点抽样的方式,计算轨迹的距离基准值:

步骤4.1、根据目标的平面数据集S及所得压缩率r，在目标的平面数据集S中每隔r个点抽取一个点组成{S₁，S_1+r…S_1+(m-1)r}集合，并计算相邻两点的距离，距离计算的方法为：

其中，(x_i,y_i)为S_i的坐标，(x_i+1,y_i+1)为S_i+1的坐标；

步骤4.2、距离基准值的计算方法为：

其中，v表示步骤3运行的次数，d_ir为步骤4中距离计算公式所得的S_i和S_i+r之间的距离，其中i∈[1,m]，为兼顾数据准确性及计算的高效性，本实施例中j取2，Δd表示距离基准值等于精确到百位的相邻抽样点的距离均值；

步骤5、分组及跨区关键点识别：上述动态数组的数据是可变，其数据来源于分组数据，是其子集，最终符合要求的动态分组即是关键点集合了，所谓的按域分组，是将原始数据按距离基准值对轨迹位置点进行分组，则所有按域分组的数据总和为原始数据，采用上述的距离基准值为正方形边长对平面进行分区，并用每个最小正方形中的最大横、纵坐标来标识该分区，同时标记每个位置数据所在的分区坐标，然后将时间连续且分区一致的位置点归并一组，并标识分组中时间最前的位置点为跨区关键点：

按步骤4所得的距离基准值Δd，在平面直角坐标系中，以(0,0)为起始点，以Δd为边长，对平面进行正方形分区，将点(0,0)所在的分区标记为(0,0)，点(Δd，Δd)所在分区标记为(1,1)，该正方形分区是以距离基准为边长，右上边界为实线、左下边界为虚线的区域。分布于正方形分区内的坐标点，以及分布在正方形右上边上的坐标点均可以描述为坐落于该分区内，依次类推，下面给出位置点(x_d,y_d)所在分区(X_d,Y_d)的计算方法：

根据上述公式，可将目标的平面数据集S中的位置点进行分区坐标转换，并将时间连续且分区标记一致的位置点归为一组，由于目标是周期性位置数据上报，所以，上述时间连续表示两个位置点是前后顺序上报；

将每组第一个位置点标记为跨区位置点，并构造位置点的数组元素Data，其Stat属性都置为0，跨区位置点是分组关键路径的起始点，是关键位置点的一种，而且一个分区有且仅有一个跨区位置点，然后将数组元素Data依次存入动态数组M₁中；

步骤6、按域分的组内关键路径的计算：分析组内位置点的个数，如果个数小于阈值(例如3)，则将组内的位置点都视为关键位置点，并跳过本组的压缩直接进入下一组的组内分析，计算位置点与该点前两个位置点的运动状态表达式，通过分析可确定该位置点是否是运动状态同质，进而得到该分组的关键路径，识别组内关键路径，以步骤5中所得第一个分组A为例，对预判算法作进一步的说明，分组A内的位置点按时间从前到后依次标记为A₁、A₂、A₃…，并用(x_i,y_i)表示A_i的坐标：

步骤6.1、定义初始的缩减位置点个数drill为0，用以描述动态数组M₁中相邻位置点之间实际包含的位置点个数；

步骤6.2、设定分区A(x_a,y_a)的相邻位置点A₁、A₂，则连接A₁、A₂的矢量在平面坐标系的运动状态如图2所示，A₁、A₂所在直线L表达式为：y＝k(x-x₁)+y₁

其中，k为直线L的斜率，如图3所示，直线L与X轴的夹角为α，则tanα＝k；

步骤6.3、沿矢量的方向，以A₂为原点作射线A`，A`逆时针旋转得射线L₁，其中射线L₁与X轴的夹角为β，则本实施例中设定方位基准值

如图3偏转基准线的角度关系所示，根据三角函数诱导公式可知：

其中则射线L₁所在直线的表达式为：

同理，射线L₂所在直线的表达式为：

步骤6.4、作射线L₁与分区边界的交点a₁和射线L₂与分区边界的交点a₂，如图4平面矢量顺逆时针关系，由于A₃必在分区边界内，则“A₃在预判区域内”等价于“在的逆时针方向且在的顺时针方向”，其中为连接A₂指向a₁的矢量，为连接A₂指向a₂的矢量；

步骤6.5、判断两矢量相互之间的顺逆时针关系，根据矢量叉积定理，上述矢量和的顺逆时针关系，可以描述为：

(1)若则在的顺时针方向；

(2)若则在的逆时针方向；

(3)若则与共线；

其中表示与的叉积；

由于“A₃在预判区域内”等价于“且”，则A₃与的预判表达式为：且当且仅当A₃与的预判表达式为真时，A₃符合预判；

步骤6.6、A₃与的预判表达式存在为真和为假两种情况，其具体处理的方法如下：

若A₃与的预判表达式为真时，过滤A₂点，并为drill加1；若A₃与的预判表达式为假时，则视A₂点为偏转位置点，构造A₂点的数值元素Data，其Stat置为1，Drill置为drill；将A₂点的数值元素Data作为A₁的紧后点存入动态数组M₁，最后重置drill为0；

上述处理后，继续判断A₄是否符合预判，依次类推，直至判定完分组内的所有位置点；

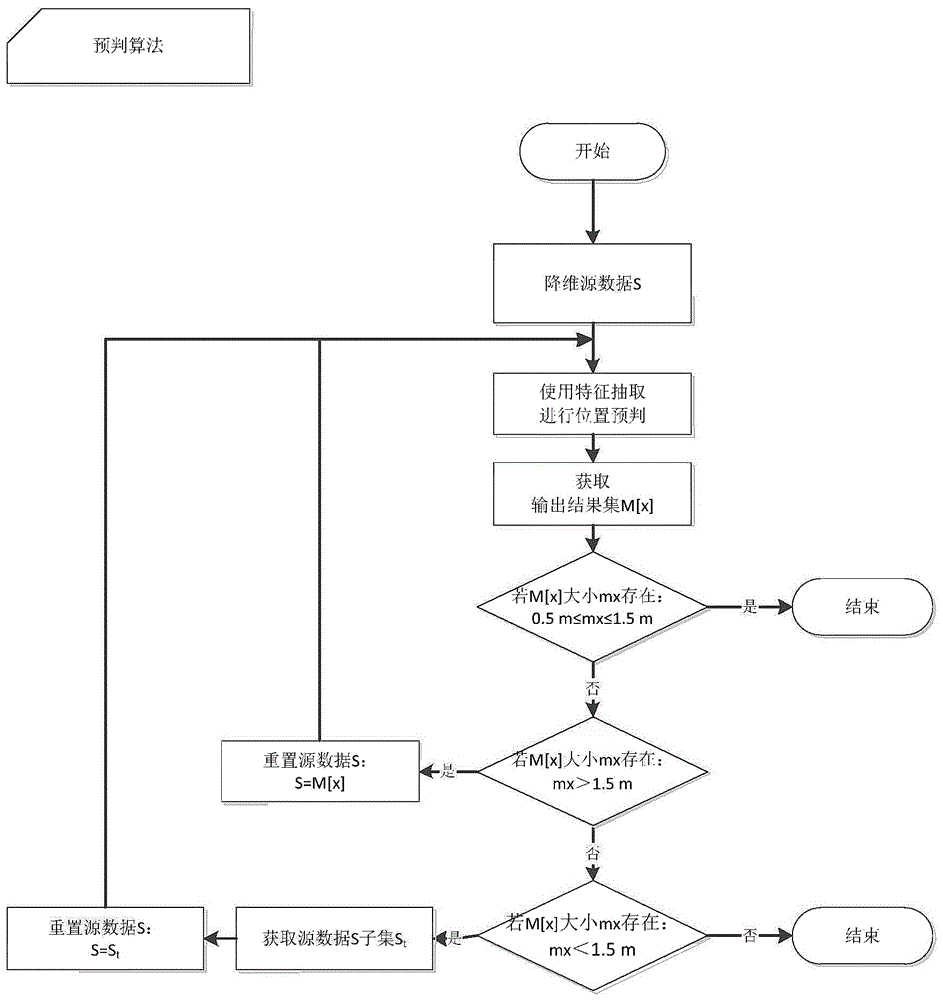
步骤7、结果合并与再分析：依照步骤6的方法得到其他分组的关键路径，按时间先后合并为第一次抽取的输出结果集M₁，记M₁的元素个数为m₁；将上述各分组的关键路径结果按时间前后合并，并分析输出结果集的数量与预期的输出结果集的比值，确定是否直接返回处理结果，如图5所示，对抽取结果进行处理分析：

(1)当满足退出条件时，结束抽取过程，并返回输出结果集M₁；

(2)当时，以动态数组M₁中Drill值最大的位置点D为结束点，位置点D的紧前点为起始，从目标的平面数据集S中获取子集S_t且不包含前述两个位置点，并按步骤3到步骤7的做法，获得子集S_t的关键路径M_t，将M_t存入动态数组M₁中紧邻位置点D之后，依次类推，当满足退出条件时，结束抽取过程，并返回输出结果集M₁；

(3)当时，将M₁视为二次抽取的数据集S₁，并从步骤3开始循环处理数据抽取的过程，直至输出结果集M₂满足退出条件时，结束抽取过程，并返回输出结果集M₂。

本发明的重点在于：对目标的关键路径识别，通过其运动轨迹的最大化留存，以及将非关键位置点的个数附加在关键点的属性中来降低输出结果集的大小，为此，首先要求能够识别目标运动的路程变化；有了均差路程后，才能对运动过程进行分区，有效降低计算的复杂度；在分区后，通过预判算法抽取目标运动过程中的关键位置点，本发明的关键路径识别方法采用了目标状态相关的距离基准和业务场景相关的偏转基准，在位置服务领域具有很强的适用性和可操作性，从整体上有效解决了位置轨迹的失真问题，在保证数据质量的基础上，降低了信息冗余，能有效地满足平台向移动应用提供位置服务的效率性和经济性。

以上仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明实施例揭露的技术范围内，可轻易想到的变化或替换，都应该涵盖在本发明的保护范围之内。