局部形状迁移指导的图像对象共分割方法与流程
本发明属于图像处理、计算机视觉技术领域,是局部形状迁移指导的图像对象共分割方法。
背景技术:
给定包含相同语义类别对象的图像集,图像对象共分割技术主要考虑如何从中分割出共同的对象,以便开展图像内容理解、对象检测等更高层次的视觉理解工作。在2006年,Rother等人首次提出图像对象共分割的概念,利用产生式模型在包含相同类别的图像对上进行对象前背景分割,该方法使用高斯模型产生潜在前景直方图,并将图像对在前景直方图的差异作为一项全局约束加入基于马尔科夫随机场的能量中,最后采用TRGC优化算法得到共分割结果。目前,多幅图像的共分割大致分为两个方向:基于统一模板学习的共分割和基于区域匹配的共分割。
基于统一模板学习的共分割方面,在2010年,Joulin等人提出了一种基于判别聚类的图像对象共分割方法,他们将现有的单张图像分割算法(归一化分割)和对象检测算法(核方法)集成到一个新的判别聚类框架中,目标是对多幅图像进行前背景分割。首先,该方法为保持单幅特定图片在空间和外观上的一致性,利用像素点的坐标及RGB颜色值作为特征计算相似度矩阵,在得到标准化拉普拉斯矩阵L后采用类似归一化分割的谱分割算法得到图像内部的分割结果;其次,该方法为使同时分割的多幅图像产生关联,使用了基于正定核的判别聚类算法实现不同图像之间前背景差异最大化;最后,该方法通过将空间一致性拉普拉斯矩阵L和判别聚类损失矩阵A进行组合,将多幅图像的共分割转化为一个组合优化问题,并通过将其松弛为连续的凸优化问题实现多幅图像共分割。然而,当共分割对象的外观模型复杂程度增大,或前景区域与背景区域十分相似时,共分割对象在全局形状上的不一致性将导致很难学习到统一的模板用于前景对象的分割,此时基于统一模板学习的共分割方法便不能很好的区分前景对象与背景区域。
基于区域匹配的共分割方面,在2013年,Wang等人提出一种一致性泛函映射方法,通过计算图像间在外观上的关联性实现多幅图像的共分割,该方法包含三个部分。第一部分:将每幅图像分割成超像素块,并将每幅图片表示为无向图,图中顶点表示超像素块,图中边的权值由超像素块公共边的长度决定,通过给每个图计算一个标准化的拉普拉斯矩阵为每幅图片生成一个维度较低的泛函空间,同时分割结果表示成包含对象的超像素块的集合。第二部分:将两幅图像之间的关联性表达成线性泛函。第三部分:联合优化分割函数产生分割结果,该过程需要匹配单幅图像上的分割先验,同时保持相邻图像间泛函映射时的一致性。该方法既可以实现无监督的共分割,也可以通过使用部分图像的真实分割结果进行有监督的共分割。基于区域匹配的共分割方法在公开数据集上取得了令人满意的结果,但前景对象在外观发生较大变化时,会极大的影响最终的分割结果。
局部形状迁移是一种广泛应用于基于数据驱动的前背景分割方法,该方法能将真实分割结果迁移到测试图像上,达到对单张测试图像进行前背景分割的目的。在2015年,Yang等人提出了一种通过局部形状迁移实现数据驱动下的对象分割方法,该方法首先输入一幅测试图像和多幅带有真实分割结果的样本图像,然后采用Barnes在2010年提出的PatchMatch方法实现以局部patch块为单位的多尺度图像匹配,通过匹配结果为测试图像上每一个局部patch块得到在其他图像上的近似局部patch块,最后采用MRF能量函数得到最终分割结果。
在2013年,Kim等人提出了一种可变形的空间金字塔匹配算法(DSP),解决了两幅图像间稠密像素点的匹配问题。该方法采用金字塔模型从整幅图像,到网格单元再到单个像素点进行多尺度的匹配,将像素点匹配结果以水平位移和垂直位移的形式进行输出。在国际公开数据集上的测试结果表明,该方法能为相同语义类别的像素点之间建立较好的匹配关系,为本方法中实现patch块的匹配提供基础。
在2000年,Roweis等人提出了一种局部线性嵌入的降维算法,并广泛应用于图像分割、图像分类等计算机视觉领域。该算法包括三个主要步骤。第一步是为每个样本点xi寻找k个邻近点,第二步是用k个邻近点计算该样本点的局部重建权重矩阵,所用误差公式如下:
第三步是由该样本点的局部重建权重矩阵将样本点映射到低维空间中,映射条件如下:
上式中,yi是样本点xi在低维空间的映射。
因此,前景对象姿态、位置、尺度发生较大变化时对象全局形状的不一致性,极大的影响了现有的图像对象共分割方法的分割效果,而本发明通过局部形状迁移指导的方法,有效避免了因对象全局形状的不一致带来的问题。
技术实现要素:
本发明的目的是:克服对象全局形状的不一致对图像对象共分割结果的影响,提出了局部形状迁移指导的图像对象共分割方法,这种方法在标准测试数据集上有良好的表现,能够较好的实现同一语义类别对象的分割。
为完成本发明的目的,本发明采用的技术方案是:
局部形状迁移指导的图像对象共分割方法,其中,包括如下步骤:
步骤(1),图像集预处理:输入M幅包含相同语义类别对象的图像,对每幅图像进行显著性分析,将显著性检测结果使用二倍均值做阈值得到mask图,即为前背景初始分割结果,其中mask图仅由0和1组成,1代表前景像素点,0代表背景像素点。
步骤(2),对任意两幅图片进行稠密特征点匹配:针对每一幅图像i(i=1,2,...,M),为图像上每一个像素点生成128维的dense sift特征;将每一幅图片i(i=1,2,...,M)的dense sift特征与其他图片j(j=1,2,...,M且j≠i)的dense sift特征进行稠密特征点匹配,得到稠密特征点的水平位移hij和垂直位移vij。
步骤(3),根据匹配结果,建立每一局部图像区域与来自其他图像的局部区域之间的对应关系:对每一幅图像i,每间隔5个像素点选取一个17*17的patch块,用中心像素点坐标表示该patch块的位置,用中心像素点的sift特征描述子表示该patch块的特征;使用步骤(2)中得到的水平位移hij和垂直位移vij,计算出每一个patch块在其他图像上与之对应的patch块的位置;构建patch块的对应关系有向图,顶点代表patch,有向边指向该patch块在其他图像上的邻居patch块。。
步骤(4),采用局部线性结构保持算法学习对应关系的权重:对于任意patch块i,根据步骤(3)中构建的对应关系有向图找到其邻居patch块集合,记为由局部线性保持原理得:
上式中,P是所有patch块数,表示patch块i的sift特征,wij为学习到的权重系数。wij的求解采用经典的局部线性嵌入(local linear embedding)算法中的构造协方差矩阵及拉格朗日乘子法进行求解。
步骤(5),通过迭代求解算法在对应局部区域之间传递其前背景分割结果,得到最终分割结果:包括最小优化方程的构造和优化算法两个主要步骤。
第一步,根据步骤(3)得到的patch块对应关系图和步骤(4)学习到的对应关系权重系数,构造如下最小优化方程式:
上式中,y表示输入的M幅图像的前背景分割结果,y[i]表示第i幅图像的前背景分割结果,表示第i个patch块的前背景分割结果,Eseg是经典的马尔科夫能量项,表示图像内部的像素点之间的关系,α为系数。
第二步,采用半二次方分裂(half-quadratic splitting)最小化方法迭代求解已构造的最小优化方程式:首先,引入辅助变量z,同时假设在任意patch块上都满足将该限制条件引入到第一步构造的方程式中得到如下优化方程式:
上式中,α和λ为系数,wij表示patchi和patchj之间的权重值。
接下来,通过固定其中一个变量求解另一个变量的方法,将上式分解为两个简单的子问题,如下所示:
对于第一个子问题:将第二项并入到MRF能量项的一次项中,并通过经典的图割算法进行优化;对于第二个子问题:通过求导的方式求解最优的解。通过不断的迭代求解y和z,将达到终止条件或最大迭代次数的y作为分割最终结果。
本发明与现有技术相比的优点在于:本发明提出的局部形状迁移指导的图像对象共分割方法,框架简单且易于实现,执行时空效率高,解决了对象全局形状不一致时分割效果不好的问题,其中,采用局部线性嵌入方法学习得到权重,为局部形状迁移提供更加鲁棒的保证。
附图说明
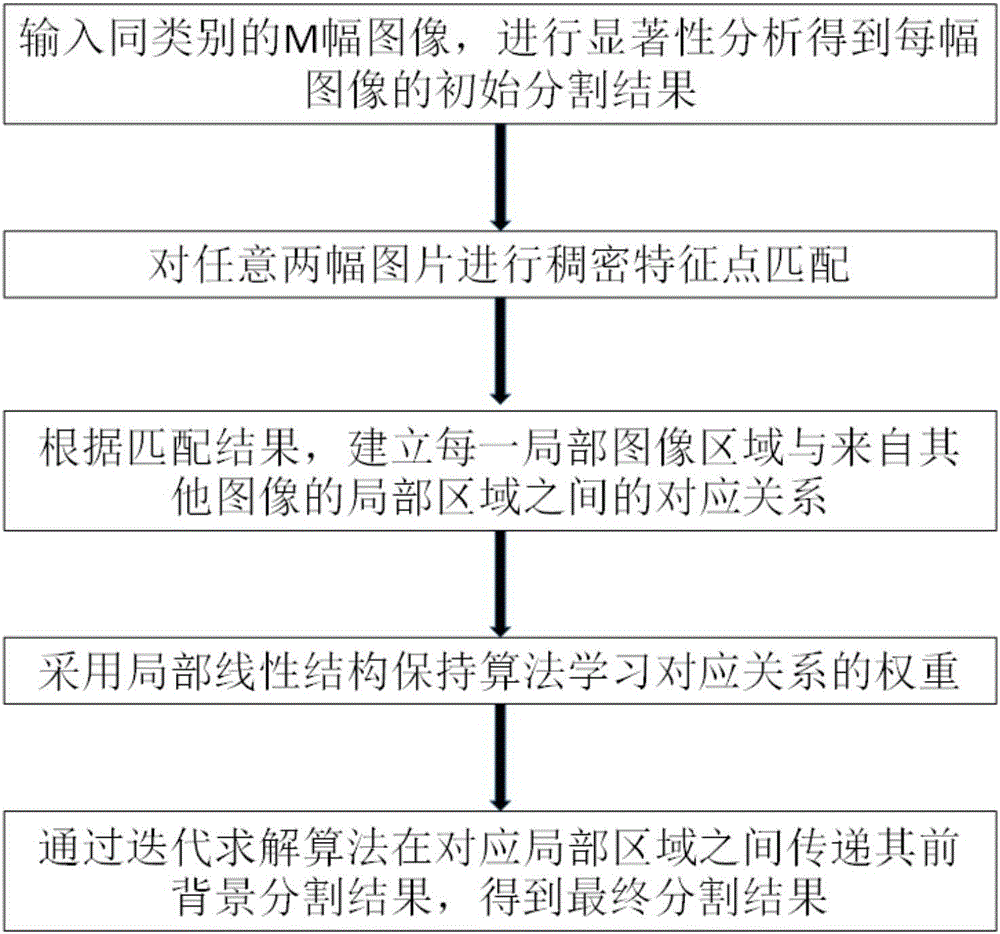
图1是本发明的流程图;
图2是本发明在公开数据集上的测试结果图。
具体实施方式
如图1所示,本发明提出了局部形状迁移指导的图像对象共分割方法,包括以下步骤:
(1)图像集预处理:输入M幅包含相同语义类别对象的图像,使用Zhang等人在2015年提出的显著性检测方法对每幅图像进行显著性分析,将显著性检测结果使用二倍均值做阈值得到mask图,即为前背景初始分割结果,其中mask图仅由0和1组成,1代表前景像素点,0代表背景像素点。
(2)对任意两幅图片进行稠密特征点匹配:针对每一幅图像i(i=1,2,…,M),为图像上每一个像素点生成128维的dense sift特征;将每一幅图片i(i=1,2,…,M)的dense sift特征与其他图片j(j=1,2,…,M且j≠i)的dense sift特征采用Kim等人在2013年提出的可变形的空间金字塔匹配算法(DSP)进行稠密特征点匹配,得到稠密特征点的水平位移hij和垂直位移vij。
(3)根据匹配结果,建立每一局部图像区域与来自其他图像的局部区域之间的对应关系:对每一幅图像i,每间隔5个像素点选取一个17*17的patch块,用中心像素点坐标表示该patch块的位置,用中心像素点的sift特征描述子表示该patch块的特征;使用步骤(2)中得到的水平位移hij和垂直位移vij,计算出每一个patch块在其他图像上与之对应的patch块的位置;构建patch块的对应关系有向图,顶点代表patch块,有向边指向该patch块在其他图像上的邻居patch块。
(4)采用局部线性结构保持算法学习对应关系的权重:对于任意patch块i,根据步骤(3)中构建的对应关系有向图找到其邻居patch块集合,记为由局部线性保持原理得:
上式中,P是所有patch块数,表示patch块i的sift特征,wij为学习到的权重系数。wij的求解采用经典的局部线性嵌入(local linear embedding)算法中的构造协方差矩阵及拉格朗日乘子法进行求解。
(5)通过迭代求解算法在对应局部区域之间传递其前背景分割结果,得到最终分割结果:包括最小优化方程的构造和优化算法两个主要步骤。
第一步,根据步骤(3)得到的patch块对应关系图和步骤(4)学习到的对应关系权重系数,构造如下最小优化方程式:
上式中,y表示输入的M幅图像的前背景分割结果,y[i]表示第i幅图像的前背景分割结果,表示第i个patch块的前背景分割结果,Eseg是经典的马尔科夫能量项,表示图像内部的像素点之间的关系,α为系数。
第二步,采用半二次方分裂(half-quadratic splitting)最小化方法迭代求解已构造的最小优化方程式:首先,引入辅助变量z,同时假设在每一patch块上都满足将该限制条件引入到第一步构造的方程式中得到如下优化方程式:
上式中,α和λ为系数,在本实验中设置为α=1,λ=0.3;wij表示patchi和patchj之间的权重值。
接下来,通过固定其中一个变量求解另一个变量的方法,将上式分解为两个简单的子问题,如下所示:
对于第一个子问题:将第二项并入到MRF能量项的一次项中,并通过经典的图割算法进行优化;对于第二个子问题:对求导,得到下式:
将上式转化为矩阵形式如下:
Z'={λY+α[W+WT-WTW+Diag(WTW)]Z}[(α+λ)I+Diag(WTW)]-1,
上式中,矩阵Z,Z',Y分别由列向量连接而成;W是大小为P*P的矩阵,其数值代表patch块之间的权重;I是单位矩阵;Diag(·)运算实现创建对角矩阵,其非零元素为输入矩阵对角线上的元素。
通过对上式进行不断迭代求解得到Z,实验中设置迭代次数为15,每次迭代中都将Z归一化到[0,1]之间。
最后,将最大迭代次数设置为10,使用y在两次迭代结果之间的差异不超过M幅图像像素点总数的0.0001倍作为迭代终止条件,通过不断的迭代求解两个子问题中的y和z,并将达到迭代终止条件或者达到最大迭代次数的y作为最终分割结果。图2所示为部分共分割结果,即(a)(b)(c)(d)四组,每组中上方为原始图像,下方对应共分割结果。
- 还没有人留言评论。精彩留言会获得点赞!