一种基于幅频特征稀疏滤波的图像分类方法与流程
本发明涉及的是一种图像分类的方法,具体可以应用到各种需要图像分类的场景中。
背景技术:
稀疏滤波技术,是指通过约束信号重构系数矢量中非零系数的个数,达到优化特征表达,提高计算速度的效果,此外,稀疏滤波可以对信号产生压缩效果,以此节约存储和传输空间。
稀疏滤波应用到图像分类中,就是用图像信号的稀疏特征系数代替图像本身作为分类的信号样本。对于基于稀疏滤波的图像分类技术来说,常用做法是采用矩阵分解技术,通过将原始图像像素矩阵X分解为两个矩阵U和A的乘积,其中,矩阵U为基矩阵,控制图像特征由高维向低维转化,矩阵A为稀疏系数矩阵,其中每一列系数矢量中,存在极少数的非零元素,训练稀疏模型时,采用L-1范数约束稀疏系数矩阵A的稀疏度,分类时,使用图像信号的稀疏系数矩阵作为分类器的输入,分类图像。这种方式的缺点在于:一,对矩阵A做L-1范数稀疏度约束,容易使学习到的模型产生过拟合,影响分类的效果,甚至,严重时会产生错误分类,在分类结果与安全因素相关时,会导致严重的安全灾难;二,如果对矩阵U做过拟合惩罚,则增加了优化项,使优化过程复杂化,需要昂贵的计算资源。
图像的幅频特征,是指将图像信号或者可以代表图像信号的特征信号作为二维信号进行调和分析,使用诸如离散傅里叶变换,Z变换,小波变换,希尔伯特-黄变换等手段,获取到的图像数据在频率域的特征,是信号幅度与信号频率之间的关系。利用图像的幅频特征进行稀疏滤波,可以在利用图像信号的频率特性建立滤波模型,避免直接对矩阵A和矩阵U做约束,从而有效地避免了过拟合和优化过程的复杂化。
技术实现要素:
本发明提供一种基于幅频特征稀疏滤波的图像分类技术,利用图像信号的幅频特征建立稀疏滤波模型;利用稀疏特征矩阵进行图像分类。
本发明技术方案为:
一种基于幅频特征稀疏滤波的图像分类方法,包括以下步骤:
1)训练数据获取阶段,获取待分类图像数据的一个子集,格式化为统一维度的图像数据矩阵X;
2)初始化阶段,生成两个随机矩阵,分别为维度为f*n的基矩阵U,维度为n*m的稀疏系数矩阵A;
3)变换阶段,对矩阵A或图像数据矩阵X进行调和变换,获得幅频特征矩阵F;
4)优化建立阶段,通过约束原始矩阵X与重构矩阵Y=UA的能量差最小,以及幅频特征矩阵F的能量最大,选取一种优化算法,执行迭代优化,例如,可以选取梯度下降算法;
5)优化迭代阶段,重复执行4,直到目标函数值达到预期的目标或者迭代次数达到预先设定的最大值;
6)生成阶段,用基矩阵U和新的待分类图像矩阵Z,生成矩阵Z的稀疏系数矩阵B;
7)分类阶段,选择一种分类器,矩阵B作为分类器输入,获取分类结果。
本发明的有益效果为:一种基于幅频特征稀疏滤波的图像分类技术具有非常广泛和实用的应用场景,比如,在生产环境中,由于传感器采集到的图像数据都是带有随机噪声和自然背景的图像数据,这些数据会放大L-1范数稀疏度约束的过拟合效果,严重干扰图像分类结果。基于幅频特征的稀疏滤波方法,通过在频域建立稀疏滤波模型,有效避免了直接约束稀疏系数矩阵带来的过拟合问题,并且通过减少优化项,提高了优化效率,不但节省了计算资源,而且提高了分类器的分类精度,因此,具有广阔的应用前景。
附图说明
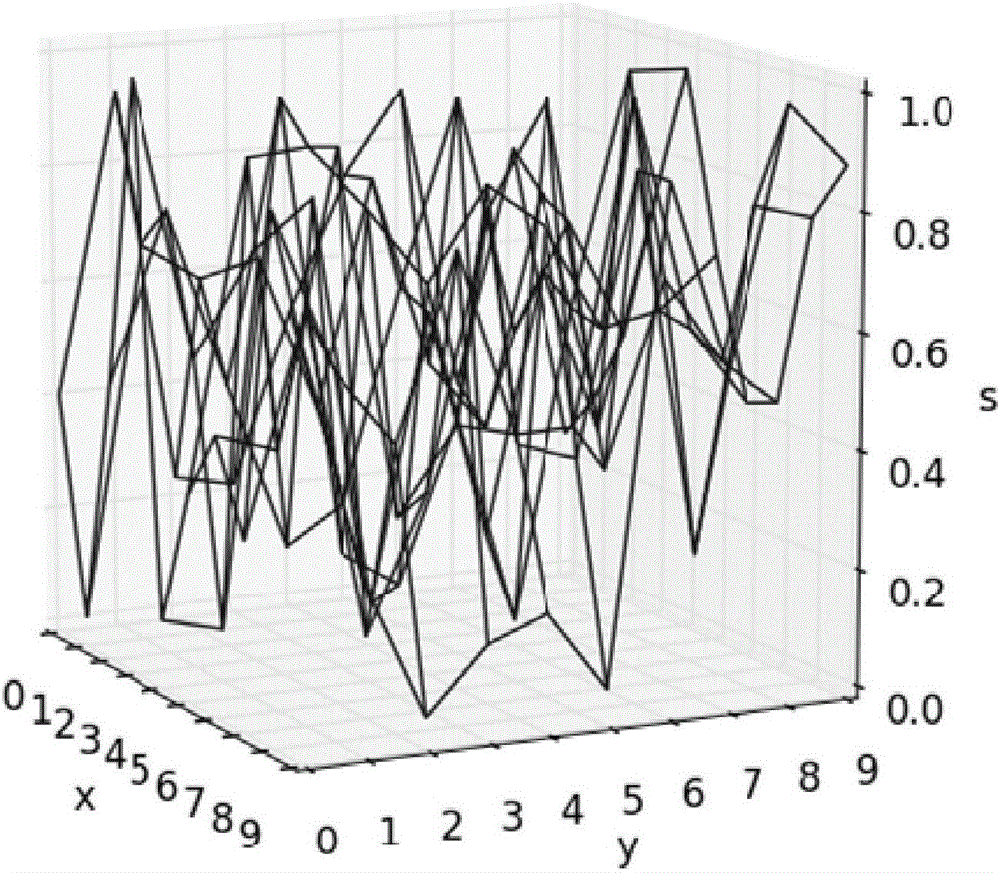
图1(a)为稀疏度为α的矩阵A的图像;
图1(b)为图1(a)中矩阵A的幅频特征矩阵F的图像;
图2(a)为稀疏度为β的矩阵A的图像;
图2(b)为图2(a)中矩阵A的幅频特征矩阵F的图像
图3(a)为稀疏度为γ的矩阵A的图像;
图3(b)为图3(a)中矩阵A的幅频特征矩阵F的图像
图中:x,y分别为矩阵A两个维度坐标;s代表矩阵A的二维信号函数值;u,v分别为矩阵F的两个维度坐标;稀疏度α<β<γ。
具体实施方式
下面结合附图和技术方案详细说明本发明。
第一步,训练数据获取阶段
获取待分类图像数据之后,选取一个子集作为训练数据,格式化为m*(w*h)维度的图像数据矩阵X;其中,m为样本数目,w、h为单个图像的长、宽;设f=w*h为图像原始特征空间维度,即待分类图像中像素点的个数;
第二步,初始化阶段
设置稀疏特征数目为n(n<f),随机生成元素数值在0~1之间的两个二维矩阵,分别为维度为f*n的基矩阵U和维度为n*m的稀疏系数矩阵A;
第三步,变换阶段
对稀疏系数矩阵A或者图像数据矩阵X进行调和变换,获得幅频特征矩阵F;所述的调和变换的方法包括离散傅里叶变换、快速傅里叶变换、离散余弦变换、Z变换、小波变换或希尔伯特-黄变换等;
假设采用稀疏系数矩阵A执行离散傅里叶变换,用s(x,y)代表A的二维信号函数,F(u,v)代表s(x,y)的幅频特征,则:
其中,u,v代表F的两个维度坐标,x,y代表A两个维度坐标,m为样本数目,n为稀疏特征数目。
第四步,优化建立阶段
将幅频特征矩阵F的协方差矩阵的和的L-2范数的相反数作为F的能量,记为E(F);设幅频特征矩阵F的第i个列向量的协方差矩阵为R(Fi),则稀疏度约束函数spi=λ||X-UA||2+E(F)。其中,λ为能量约束系数,一般取0.5;重构矩阵Y=UA为基矩阵U和稀疏系数矩阵A的乘积;i、j分别表示幅频特征矩阵F的维度坐标。
第五步,优化迭代阶段
以稀疏度约束函数为目标函数,根据约束目标函数中图像数据矩阵X(原始矩阵)与重构矩阵Y的能量差最小,以及幅频特征矩阵F的能量最大,选取梯度下降算法,执行迭代优化。
所述的梯度下降算法具体为:
目标函数spi对稀疏系数矩阵A,基矩阵U的梯度更新矩阵函数分别为:
Gspi/U=-XAT+(UA)AT
设置迭代次数,通过以上两个梯度更新矩阵,执行以spi函数为目标函数的迭代优化,至目标函数值达到预期的目标或者迭代次数达到预先设定的最大值,梯度下降算法结束。
附图是对迭代优化过程中,幅频特征矩阵与稀疏系数矩阵变化趋势的说明,图1(a)、图2(a)、图3(a)为稀疏度递增的稀疏系数矩阵A的图像;图1(b)、图2(b)、图3(b)分别为图1(a)、图2(a)、图3(a)中矩阵A的幅频特征矩阵F的图像;随着图1(b)、图2(b)、图3(b)中幅度偏离中心程度的逐渐变大,相应地,图1(a),图2(a),图3(a)的稀疏度逐渐变大。
第六步,生成阶段
设新的待分类图像数据矩阵为Z,由第五步得到的基矩阵U和待分类图像数据矩阵Z生成矩阵Z的稀疏系数矩阵B,即B=U-1Z。
第七步,分类阶段
将稀疏系数矩阵B作为分类器的输入矩阵,执行分类。
- 还没有人留言评论。精彩留言会获得点赞!