一种基于信息熵的超高维数据降维算法的利记博彩app

本发明属于高维数据预处理领域，更为具体地讲，是一种基于信息熵改进的超高维数据降维算法。

背景技术：

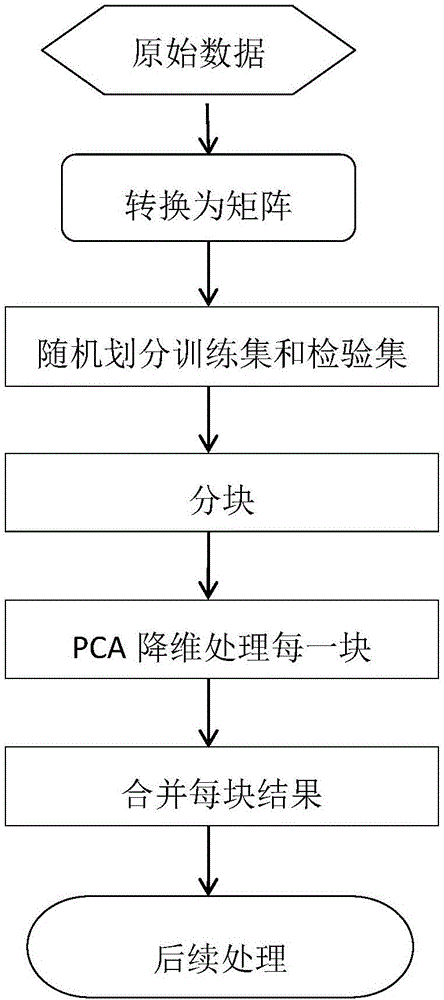
随着信息科学技术的飞速发展，信息的表示越来越全面，人们获取数据越来越容易、关注的数据对象日渐复杂，业界对数据分析、处理技术的需求最为迫切，特别是对高维数据的分析与处理技术。直接处理高维数据会面临以下困难：维数灾难、空空间、不适定、算法失效。本发明针对数据特征维太高，内存受限，不能一次性读入内存分析计算的问题，采用分块处理方法，处理流程如图1所示。但结果显示，运行耗时太长，不能满足应用需求，在此基础上，引入信息熵，首先做特征筛选，大大降低了特征数量，再做降维处理，具体流程如图2所示，具体算法如图3所示，整个过程运行耗时减少数倍，降维结果保留了大部分主成分，依然能满足应用需求。

技术实现要素：

本发明的最终目的是对原始超高维数据进行降维处理，使得降维后的数据可以在较低内存，用时较少的情况下得以继续分析处理。本发明对主要利用了信息熵在信息处理上的意义，对PCA算法进行了改进。所谓的数据维数就是每条记录数据的属性个数。

为实现上述目的，本发明基于信息熵对PCA算法做了改进， 其算法构成如下：

1)Matrix＝getMatrix(rdata)

2)计算信息熵，做筛选

3)分割数据矩阵

[B,C]＝randomSplit(Matrix)//B为训练集,C为检验集

4)样本B矩阵中心化：即每一维度减去该维度的均值

X＝B–repmat(mean(B,2),1,m1)

5)计算不同维度之间的协方差，构成协方差矩阵：

C＝(X*X^T)/size(X,2)

6)计算协方差矩阵的特征向量eigenVector和特征值eigenValue

[eigenVector,eigenValue]＝eig(Cov)

7)选择最大的k个特征值对应的k特征向量分别作为列向量组成特征向量矩阵V_n×k，k由f计算。

8)计算降维结果：Y＝V^T*X

9)对矩阵C中心化，得X0

10)计算结果：Y0＝V^T*X0

11)后续对比，如分类。

附图说明

图1是基于分块的PCA处理高维数据的流程(应用PCA的处理流程)，图2是本发明基于信息熵的PCA降维处理流程(基于信息熵的降维处理流程)，图3是本发明算法E-PCA的步骤(基于信息熵的PCA(E-PCA)算法过程)。

具体实施方式

下面结合附图对本发明的具体实施方式进行描述，以便本领域的技术人员更好的理解本发明。需要特别提醒注意的是，在以下的描述中，当已知功能和设计的详细描述也许会淡化本发明的主要内容时，这些描述在这里将被忽略。

图1是本发明基于信息熵的超高维数据降维处理的流程。在本实施例中，如图2所示，原始数据作为输入，如果原始数据本来就是属性和记录组成的矩阵，可以省略转换为矩阵的步骤。

生成矩阵的下一步为对每个属性计算信息熵H(i)，并和阈值et(et根据具体的应用取值)比较，大于阈值的属性保留，处理之后的矩阵A作为下一步处理的输入。

信息熵处理之后的数据进入PCA处理流程，首先样本中心化，在计算不同属性之间的协方差，形成协方差矩阵，再计算协方差矩阵的特征值和特征向量，计算贡特征值献率(表征获取的主成分占原始数据信息的比例)f确定k值，进而确定主成分个数，抽取最大的k个特征值对应的k个特征向量作为变换基，将原始数据降维得结果Y_k×m，以便后续分析计算。

尽管上面对本发明说明性的具体实施方式进行了描述，以便于本技术领域的技术人员理解本发明，但应该清楚，本发明不限于具体实施方式的范围，对本技术领域的普通技术人员来讲，只要各种变化再所附的权利要求限定和确定的本发明的精神和范围内，这些变化是显而易见的，一切利用本发明构思的发明创造均在保护之列。