一种快速确定复杂不解析不确定性问题随机性的分析方法与流程

本发明涉及复杂工程问题技术领域，特别是一种快速确定复杂不解析不确定性问题随机性的分析方法。

背景技术：

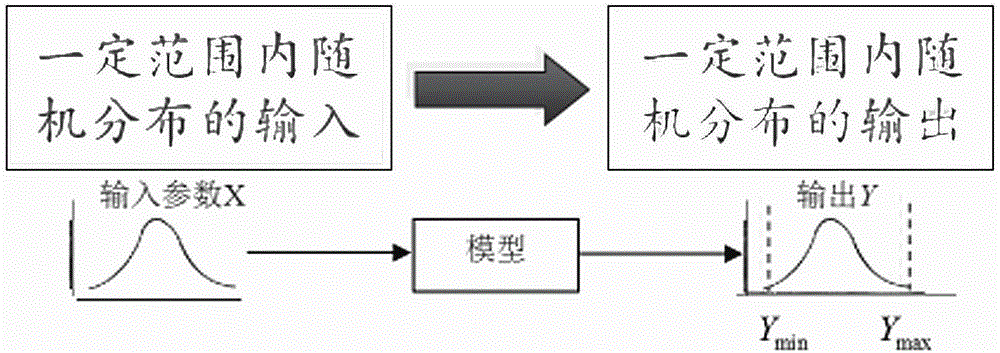
对于通常工程问题，其函数往往是各种影响因素的不解析函数，其输出往往需要通过较大的计算量进行数值求解，而且其函数模型通常比较复杂，假设其函数为Y＝f(X)，其中X＝[X₁,X₂,...X_n]为随机向量，Y为该复杂工程问题的模型输出。如图1所示，输出参数X不确定导致输出函数Y亦不确定，

针对复杂工程问题函数的随机不确定性，最广泛采用的是蒙特卡洛抽样及其改进方法(如：拉丁超立方抽样法)。上述方法通过计算每个随机样本对应的函数输出(即样本输出)，进而获得样本的统计信息，如：计算均值，方差等，该类方法简单易用，但是样本选择具有一定的随机性，降低了样本提供的信息量，往往需要综合大量的样本才能获得有效的信息，从而导致计算效率很低，即：对大量的样本逐个计算其函数输出，从而导致统计计算结果收敛相当慢。对于工程复杂问题，单次数值求解本身耗时较大，再此基础上进行大规模循环多次计算，则难以进行，因此，蒙特卡洛抽样及其改进方法不利于工程应用。

有鉴于此，本发明人提出一种快速确定复杂不解析不确定性问题随机性的分析方法。

技术实现要素：

本发明为解决上述问题，提供了一种快速确定复杂不解析不确定性问题随机性的分析方法，以少量样本点获得复杂工程问题函数的概率统计信息，从而减少函数求解次数，大大提高计算效率。

为实现上述目的，本发明采用的技术方案为：

一种快速确定复杂不解析不确定性问题随机性的分析方法，包括以下步骤：

步骤一、对随机向量X进行抽样，得到N个测试样本，并组成X^测试，X^测试表示为：

步骤二、高效初始样本集构建及其测试样本统计

首先将原始空间中的随机向量X＝[X₁,X₂,...X_n]转化成标准正态空间中的标准随机向量u＝[u₁,u₂,...u_n]，标准随机向量u中每个子分量u_i与随机向量X的每个子分量X_i的关系如下：

式中，和分别为随机向量X的第i个分量X_i均值和标准差；

在标准正态空间中的初始样本选择如下：

式中μ_i和σ_i分别为标准随机向量u的第i个子分量u_i的均值和标准差，j为1-M；M值为3，5，7或9，Floor()表示括号内的数值圆整到最近的正整数；

然后将标准空间中的每个初始样本转变成原始空间的随机向量去除该该初始样本中重复的样本，剩下未重复的初始样本总数为Num＝(M-1)*n+1；这里假设标准空间内未重复的初始样本为u^m(m＝1～Num)，对应的原始空间内未重复的初始样本则为X^m(m＝1～Num)；

接着将X^m(m＝1～Num)带入Y＝f(X)计算获得每个初始样本X^m(m＝1～Num)对应的函数输出Y^m(m＝1～Num)；

接着将标准空间内的初始样本u^m(m＝1～Num)和函数输出Y^m(m＝1～Num)组成初始样本集B₀＝{u^m,Y^m}(m＝1～Num)；

接着利用Kriging模型建立标准空间内随机向量u与函数输出Y之间的解析函数这里k表示Kriging模型的重构次数，当k＝0时，表示该解析函数的Kriging模型是根据初始样本集B₀构建的；

然后结合和式计算测试样本X^测试的函数值响应Y^测试，将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A₀＝{X^测试,Y^测试}；

接着，对该测试样本集A₀中的Y^测试进行统计，计算对应的均值和标准差

步骤三、基于Kriging建模的复杂工程函数重构及其新样本选择与测试样本统计

首先，通过优化求解式maxσ_y(u)·F(u)·V(u)获得新的样本；其中，σ_y(u)为在随机向量u位置对应的预测函数值的误差标准差，在计算随机向量u对应的时，同时获得σ_y(u)的评估值，F(u)为随机向量u的联合概率密度分布函数，其表示如下：

式中，μ_u为随机向量u的均值，V(u)为随机向量u各个子分量u_i与现有样本集中各个样本u^m(m＝1～Num)的各子分量最短距离的一半D_i所围成的超椭圆球体积，其中由于得到优化求解式

对优化求解式进行求解得到优化解为利用数值计算优化解对应的函数值响应将新的样本及其对应的函数响应值增加到样本集B_k-1中，得到新的样本集B_k，同时令Num＝Num+1，用于表示新样本B_k中样本的总数，当k＝0时，B_k即为初始样本集B₀；

最后，基于Kriging模型对该新的样本集B_k进行建模，获得对应的新的解析函数结合式和新的解析函数计算测试样本X^测试的函数值响应Y^测试，将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A_k＝{X^测试,Y^测试}；

对测试样本集A_k中的Y^测试进行统计，计算对应的均值和标准差

步骤四、收敛性判断

先通过以下判断公式来判断复杂工程问题函数的随机性统计结果是否收敛，如果同时满足式判断公式则停止计算，否则重复步骤三，判断公式为：

最后，用复杂工程问题函数的均值和标准差来表示概率随机性统计信息。

所述优化求解式采用粒子群优化算法进行求解，以获得其全局优化解

所示步骤四中，判断公式中的ε为比较小的数值，较小数值指多次反复试算确定的偏小且合适的数值。

采用上述方案后，本发明的有益效果是：以少量样本点获得复杂工程问题函数的概率统计信息，从而减少函数求解次数，大大提高计算效率，并且还存在以下特点：

1、提出高效初始样本的选择方法；

2、提出新样本的选择方法，包括综合新样本的预测标准差、概率密度以及新样本所在位置的超椭球体积的大小这三方面信息确定新样本点的位置；

3、通过Kriging模型不断重构近似逼近复杂工程问题的函数；

4、通过比较均值和标准差计算结果，判断计算是否收敛；

附图说明

此处所说明的附图用来提供对本发明的进一步理解，构成本发明的一部分，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。附图中：

图1输入参数不确定导致模型输出亦不确定的示意图；

图2和3是是载荷作用在屋架结构的示意图。

具体实施方式

为了使本发明所要解决的技术问题、技术方案及有益效果更加清楚、明白，以下结合附图及实施例对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

本发明的一种快速确定复杂不解析不确定性问题随机性的分析方法，包括以下步骤：

步骤一、对随机向量X进行抽样，得到N个测试样本，并组成X^测试，如下所示：

步骤二、高效初始样本集构建及其测试样本统计

首先，将原始空间中的随机向量X＝[X₁,X₂,...X_n]转化成标准正态空间中的标准随机向量u＝[u₁,u₂,...u_n]，标准随机向量u中每个子分量u_i与随机向量X的每个子分量X_i的关系如下：

式中，和分别为随机向量X的第i个分量X_i均值和标准差；

在标准正态空间中的初始样本选择如下：

式中，μ_i和σ_i分别为标准随机向量u的第i个子分量u_i的均值(为0)和标准差(为1)，j为1-M；M值通常指定为3，5，7或9，Floor()表示括号内的数值圆整到最近的正整数；

借助，对于标准空间中的每个初始样本可以通过式(2)转变成原始空间的随机向量去除该该初始样本中重复的样本，剩下的未重复的初始样本总数为Num＝(M-1)*n+1；这里假设标准空间内未重复的初始样本为u^m(m＝1～Num)，对应的原始空间内未重复的初始样本为X^m(m＝1～Num)；

然后，通过数值计算可以获得每个初始样本X^m(m＝1～Num)对应的函数输出Y^m(m＝1～Num)；

接着将标准空间内的初始样本u^m(m＝1～Num)和函数输出Y^m(m＝1～Num)组成初始样本集B₀＝{u^m,Y^m}(m＝1～Num)；

接着利用Kriging模型建立标准空间内随机向量u与函数输出Y之间的解析函数这里k表示Kriging模型的重构次数，当k＝0时，表示该解析函数的Kriging模型是根据初始样本集B₀构建的；

然后结合和式(2)计算测试样本X^测试的函数值响应Y^测试，将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A₀＝{X^测试,Y^测试}；

接着，对该初始样本集A₀中的Y^测试进行统计，计算对应的均值和标准差

步骤三、基于Kriging建模的复杂工程函数重构及其新样本选择与测试样本统计

首先，通过优化求解式(4)获得新的样本。

maxσ_y(u)·F(u)·V(u) (4)

式中，σ_y(u)为在随机向量u位置对应的预测函数值的误差标准差。在计算随机向量u对应的时，可以同时获得σ_y(u)的评估值，F(u)为随机向量u的联合概率密度分布函数，F(u)表达式如下：

式中，μ_u为随机向量u的均值，中V(u)为随机向量u各个子分量u_i与现有样本集中各个样本u^m(m＝1～Num)的各子分量最短距离的一半D_i所围成的超椭圆球体积，D_i定义如下：

进一步有：

结合式(6)和式(7)，式(4)可以等效如下：

对于式(8)一般采用粒子群优化算法进行求解，以便获得其全局解，由于粒子群优化算法比较成熟，这里不再介绍，这里假设式(8)的优化解为

接下来，利用数值计算优化解对应的函数值响应，假设为将新的样本及其对应的函数响应值增加到样本集B_k-1中，得到新的样本集B_k，同时另Num＝Num+1，用于表示新样本B_k中样本的总数。当k＝0时，B_k即为初始样本集B₀；

接着，基于Kriging模型方法对该新的样本集B_k进行建模，获得对应的新的解析函数

结合式(2)和新的解析函数计算测试样本X^测试的函数值响应Y^测试，再将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A_k＝{X^测试,Y^测试}；

对测试样本集A_k中的Y^测试进行统计，计算对应的均值和标准差

步骤四、收敛性判断

通过判断公式(9)和(10)判断复杂工程问题函数的随机性统计结果是否收敛，如果同时满足式(9)和(10)则停止计算，否则重复步骤三，判断公式为：

其中ε为比较小的数值，比如取0.01等。

以下是本发明的两个应用实例：

实施例一：对于Y＝f(X)，随机向量X＝[X₁,X₂,...X_n]，X₁～N(0,1)，X₂～N(0,1)，P＝1，求Y的均值和标准差。

该函数具有较强的非线性，为确定复杂工程问题函数的随机概率不确定，主要按照下述四个步骤进行：

步骤一、对随机向量X进行随机抽样，得到10000个测试样本，并组成X^测试，如下所示：

步骤二、高效初始样本集构建及其测试样本统计

取M＝3，按照式(3)选择标准空间内的样本，并去除重复的样本，剩下的样本u^m如表一所示：

表一标准空间内的初始样本u^m

通过式(2)可以获得标准空间内的初始样本u^m对应的原始空间内的初始样本X^m，并通过数值计算计算初始样本X^m对应的函数响应值Y^m。

然后将标准空间内的初始样本u^m(m＝1～Num)和函数输出Y^m(m＝1～Num)组成初始样本集B₀＝{u^m,Y^m}(m＝1～Num)。

这里初始样本集B₀中的每个样本见表二。

表二实例一种初始样本集B₀

接着利用Kriging模型建立初始样本集B₀对应的近似解析函数并利用该解析函数和式(2)计算测试样本X^测试的函数值响应Y^测试。将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A₀＝{X^测试,Y^测试}。

最后，对该初始样本集A₀中的Y^测试进行统计，计算对应的均值和标准差

步骤三、基于Kriging建模的复杂工程函数重构及其新样本选择与测试样本统计

首先利用粒子群算法优化求解式(8)，得到新的样本利用数值计算优化解对应的函数值响应，假设为将新的样本及其对应的函数响应值增加到样本集B_k-1中，得到新的样本集B_k，同时另Num＝Num+1，用于表示新样本B_k中样本的总数。当k＝0时，B_k即为初始样本集B₀；

接下来，基于Kriging模型方法对该新的样本集B_k进行建模，获得对应的新的解析函数

结合式(2)和新的解析函数计算测试样本X^测试的函数值响应Y^测试，将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A_k＝{X^测试,Y^测试}；

对测试样本集A_k中的Y^测试进行统计，计算对应的均值和标准差

步骤四、收敛性判断

通过式(9)和(10)判断复杂工程问题函数的随机性统计结果是否收敛。如果同时满足式(9)和(10)则停止计算，否则重复步骤三，

其中ε为比较小的数值，这里取0.01即可；

最后，用复杂工程问题函数的均值和标准差来表示概率随机性统计信息。

经计算，该方法在5个初始样本的基础上，经过7次重构，共计算函数12次，其计算结果见表三，可以发现，本文方法计算结果拉丁超立方法和蒙特卡洛法相近，但是函数计算次数远小于后两者，因此计算效率很高。

表三三种计算方法计算结果

实例二：图2和图3所示屋架结构要求在载荷作用下的C的扰度变形大小的随机概率分布情况，该C点的扰度变形Δ_C(q,Ac,Ec,As,Es,l)是载荷q、混凝土横截面积AC、钢杆横截面积AS、混凝土弹性模量EC、钢杆弹性模量ES和长度的l函数。需要通过有限元数值计算进行求解，上述各个影响因素的概率分布信息见表四；

表四实例二各个影响因素的概率参数分布

为确定复杂工程问题函数Δ_C的随机概率不确定，主要按照下述四个步骤进行：

步骤一、令随机向量X＝[X₁,X₂,...X₆]＝[q,l,As,Ac,Es,Ec]，并进行随机抽样，得到10000个测试样本，并组成X^测试，如下所示：

步骤二、高效初始样本集构建及其测试样本统计

取M＝3，按照式(3)选择标准空间内的样本，并去除重复的样本，剩下的样本u^m如表五所示：

表五标准空间内的初始样本u^m

通过式(2)可以获得标准空间内的初始样本u^m对应的原始空间内的初始样本X^m，并通过数值计算计算初始样本X^m对应的函数响应值Y^m。

将标准空间内的初始样本u^m(m＝1～Num)和函数输出Y^m(m＝1～Num)组成初始样本集B₀＝{u^m,Y^m}(m＝1～Num)。

这里初始样本集B₀中的每个样本见表六：

表六实例一种初始样本集B₀

接着利用Kriging模型建立初始样本集B₀对应的近似解析函数并利用该解析函数和式(2)计算测试样本X^测试的函数值响应Y^测试，将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A₀＝{X^测试,Y^测试}；

最后，对该初始样本集A₀中的Y^测试进行统计，计算对应的均值和标准差

步骤三、基于Kriging建模的复杂工程函数重构及其新样本选择与测试样本统计

利用粒子群算法优化求解式(8)，得到新的样本利用数值计算优化解对应的函数值响应，假设为将新的样本及其对应的函数响应值增加到样本集B_k-1中，得到新的样本集B_k，同时另Num＝Num+1，用于表示新样本B_k中样本的总数。当k＝0时，B_k即为初始样本集B₀。

基于Kriging模型方法对该新的样本集B_k进行建模，获得对应的新的解析函数

结合式(2)和新的解析函数计算测试样本X^测试的函数值响应Y^测试。将测试样本X^测试及其函数值响应Y^测试组合成测试样本集A_k＝{X^测试,Y^测试}。

对测试样本集A_k中的Y^测试进行统计，计算对应的均值和标准差

步骤四、收敛性判断

通过式(9)和(10)判断复杂工程问题函数的随机性统计结果是否收敛。如果同时满足式(9)和(10)则停止计算，否则重复步骤三。

其中ε为比较小的数值，较小数值指多次反复试算确定的偏小且合适的数值，这里取0.01即可。

最后，用复杂工程问题函数的均值和标准差来表示概率随机性统计信息。

经计算，该方法在13个初始样本的基础上，经过11次重构，共计算函数24次。其计算结果见表七，可以发现，本文方法计算结果拉丁超立方法和蒙特卡洛法相近，但是函数计算次数远小于后两者，因此计算效率很高。

表七三种计算方法计算结果

上述说明示出并描述了本发明的优选实施例，应当理解本发明并非局限于本文所披露的形式，不应看作是对其他实施例的排除，而可用于各种其他组合、修改和环境，并能够在本文发明构想范围内，通过上述教导或相关领域的技术或知识进行改动。而本领域人员所进行的改动和变化不脱离本发明的精神和范围，则都应在本发明所附权利要求的保护范围内。