一种新型多目标粒子群优化方法与流程
本发明主要属于多目标优化技术领域,具体涉及一种新型多目标粒子群优化方法。
背景技术:
实际工程中的优化问题通常是具有多个目标函数的多目标优化问题(multi-objective optimization problem,MOP),这些目标函数往往相互冲突,不可能同时达到最优,需要对各个优化目标进行协调和折中,得到无法比较优劣的Pareto最优解集。
受不同背景的启发,涌现了大量用于求解多目标优化问题的多目标智能优化算法。其中,粒子群算法由于参数简单、收敛速度快及易于实现等优势被广泛应用到多目标优化问题中。自Coello和Lechuga于2002年正式提出多目标粒子群(multi-objective particle swarm optimization,MOPSO)算法以来,针对多目标粒子群算法容易陷入局部最优的不足,很多学者对算法进行改进。改进算法主要目标有两个:一是如何保持Pareto解的多样性,即多样性策略改进;二是如何快速找到真实的Pareto前沿,即收敛性改进。
在多样性策略研究方面,Coello将自适应网格策略引入到MOPSO算法中用于外部档案维护;Raquel采用拥挤距离排序策略维护外部档案;Pulido和Lechuga分别利用聚类和小生境技术改善求解的性能;贾树晋利用改进的Maximin适应值函数与拥挤距离的混合多样性策略对外部档案进行维护以提高解的多样性。其中,聚类技术计算复杂度高;小生境技术中的参数难以确定;自适应网格计算代价低,但规划网格中的粒子数会对Pareto解的多样性产生影响;混合多样性策略能改善Pareto解的多样性,但会增加算法的复杂度;拥挤距离排序策略操作简单并且能够较好反映粒子的密集信息和拥挤程度,裁剪拥挤距离密集的粒子,更能维护Pareto解的多样性和分布性。
关于收敛性改进,陈民铀采用动态惯性权重和变异操作提高粒子的全局寻优能力,但在ZDT4测试函数上未获得理想、稳定的解,求解多峰问题的能力有待于提高;谢承旺提出为算法中每个粒子增加一个“扰动向量”并且改进粒子越界的处理方法,有利于粒子跳出局部最优,但同时可能会破坏粒子的进化方向;罗辞勇提出组合粒子群优化与多目标估计的混合多目标优化算法,在基准函数ZDT1~ZDT3和ZDT6上获得具有较好收敛性能的Pareto解集,但在ZDT4实例上性能适中,并且混合策略增加了算法的计算代价。
以上算法均不同程度上增强了算法的全局搜索能力,但对于多目标优化问题中多峰问题的处理,没有得到有效的解决。
技术实现要素:
针对上述问题,本发明提供一种新型多目标粒子群优化方法,所述方法基于共享学习和柯西变异,所述方法采用共享学习因子以改变粒子的速度和位置更新公式,可以提高多目标粒子群算法处理多目标优化问题时解的收敛性、多样性和分布性。
本发明是通过以下技术方案实现的:
一种新型多目标粒子群优化方法,所述方法基于共享学习和柯西变异,所述方法采用共享学习因子以改变粒子的速度和位置更新公式,并采用柯西变异算子更新粒子个体最优位置和外部档案,所述方法提高了粒子的全局搜索能力和局部寻优精度,并使算法快速接近Pareto前沿的同时避免算法早熟收敛。
进一步地,将粒子群平均最优位置C作为共享学习因子,定义为:
其中,t为当前迭代次数,M为粒子群规模,i表示第i个粒子,Pi为第i个粒子的平均最优位置。
进一步地,粒子的速度更新公式如下:
Vij(t+1)=wVij(t)+c1r1(Pij(t)-Xij(t))+c2r2(Gj(t)-Xij(t))+c3r3(Cj(t)-Xij(t)) (2)
其中,i表示第i个粒子,j表示粒子的第j维,V表示粒子的速度,t为当前迭代次数,X表示粒子的位置,P为粒子的个体最好位置,G为粒子群全局最优位置,C为粒子群平均最优位置,w被称为惯性权重,c1,c2,c3为加速系数,r1,r2,r3为[0,1]之间均匀分布的随机数。
粒子的位置更新公式如下:
Xij(t+1)=Xij(t)+Vij(t+1) (3)
进一步地,采用柯西变异算子更新粒子个体最优位置和外部档案具体为:
比较新粒子与粒子个体最优位置的Pareto支配关系,若支配,则用新粒子替代个体最优位置,若被支配,则利用柯西变异算子对粒子进行扰动,对位置超出情况作极值处理,具体操作如下:
Cauchy(0,1)=tan((rand-0.5)×π) (5)
其中,X表示粒子的位置,i表示第i个粒子,j表示粒子的第j维,Cauchy(0,1)为标准柯西分布产生的随机数,rand为[0,1]之间均匀分布的随机数。pb为变异概率,定义如下:
其中,t为当前迭代次数,MaxIt为总迭代次数。
进一步地,所述方法具体包括以下步骤:
步骤1:设定所述方法的基本参数,随机初始化粒子的速度和位置;
步骤2:根据粒子之间的Pareto支配关系初始化外部档案;
步骤3:计算外部档案中粒子的拥挤距离并对粒子进行排序,分别为每个粒子随机选择全局最优位置;
步骤4:根据式(2)和(3)更新粒子的速度和位置;
步骤5:利用柯西变异算子更新粒子个体的最优位置和外部档案;
步骤6:当外部档案中粒子数达到最大设定限度时,采用拥挤距离排序策略维护外部档案;
步骤7:判断当前迭代次数是否达到最大迭代次数,若达到,则将外部档案中粒子作为最终的Pareto最优解集输出,否则,转到步骤3。
本发明的有益技术效果:
(1)本发明提出了一种新型多目标粒子群优化方法,将共享学习因子引入粒子速度更新公式,提高了粒子的全局搜索能力和局部寻优精度;
(2)采用柯西变异算子更新粒子个体最优位置和外部档案,提高了粒子的多样性和分布性;
(3)所述方法能有效提高算法求解多目标优化问题时的运行效率,为解决实际工程应用中的多目标优化问题提供了一种新方法。本专利所提的新方法可以应用于路径规划、控制系统设计、结构优化和运筹调度等领域。
附图说明
图1粒子运动示意图;
图2为本发明算法,即MOPSO-SCM算法对ZDT1优化得到的Pareto前沿;
图3为MOQPSO-CD算法对ZDT1优化得到的Pareto前沿;
图4为MOPSO-CD算法对ZDT1优化得到的Pareto前沿;
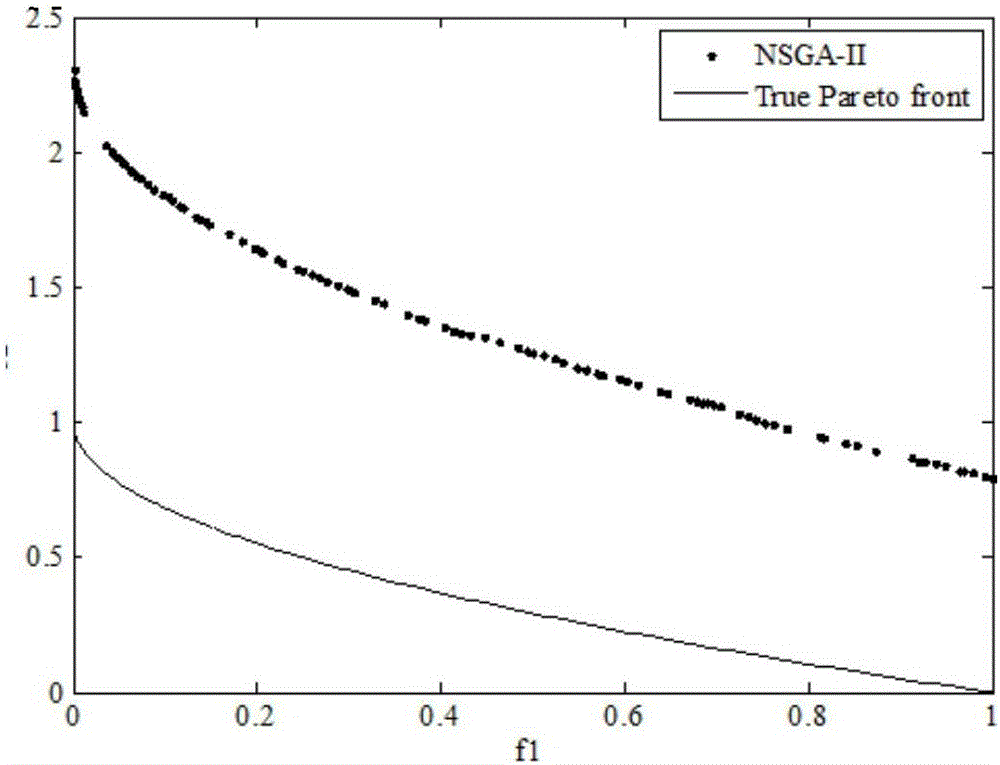
图5为NSGA-II算法对ZDT1优化得到的Pareto前沿;
图6为本发明算法,即MOPSO-SCM算法对ZDT2优化得到的Pareto前沿;
图7为MOQPSO-CD算法对ZDT2优化得到的Pareto前沿;
图8为MOPSO-CD算法对ZDT2优化得到的Pareto前沿;
图9为NSGA-II算法对ZDT2优化得到的Pareto前沿;
图10为本发明算法,即MOPSO-SCM算法对ZDT3优化得到的Pareto前沿;
图11为MOQPSO-CD算法对ZDT3优化得到的Pareto前沿;
图12为MOPSO-CD算法对ZDT3优化得到的Pareto前沿;
图13为NSGA-II算法对ZDT3优化得到的Pareto前沿;
图14为本发明算法,即MOPSO-SCM算法对ZDT4优化得到的Pareto前沿;
图15为MOQPSO-CD算法对ZDT4优化得到的Pareto前沿;
图16为MOPSO-CD算法对ZDT4优化得到的Pareto前沿;
图17为NSGA-II算法对ZDT4优化得到的Pareto前沿;
图18为本发明算法,即MOPSO-SCM算法对ZDT6优化得到的Pareto前沿;
图19为MOQPSO-CD算法对ZDT6优化得到的Pareto前沿;
图20为MOPSO-CD算法对ZDT6优化得到的Pareto前沿;
图21为NSGA-II算法对ZDT6优化得到的Pareto前沿。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本发明进行进一步详细描述。应当理解,此处所描述的具体实施例仅仅用于解释本发明,并不用于限定本发明。
相反,本发明涵盖任何由权利要求定义的在本发明的精髓和范围上做的替代、修改、等效方法以及方案。进一步,为了使公众对本发明有更好的了解,在下文对本发明的细节描述中,详尽描述了一些特定的细节部分。对本领域技术人员来说没有这些细节部分的描述也可以完全理解本发明。
实施例1
一种新型多目标粒子群优化方法,所述方法基于共享学习和柯西变异,所述方法采用共享学习因子以改变粒子的速度和位置更新公式,并采用柯西变异算子更新粒子个体最优位置和外部档案,所述方法提高了粒子的全局搜索能力和局部寻优精度,并使算法快速接近Pareto前沿的同时避免算法早熟收敛。
将粒子平均最优位置C作为共享学习因子,定义为:
其中,t为当前迭代次数,M为粒子群规模,i表示第i个粒子,Pi为第i个粒子的平均最优位置。
粒子的速度更新公式如下:
Vij(t+1)=wVij(t)+c1r1(Pij(t)-Xij(t))+c2r2(Gj(t)-Xij(t))+c3r3(Cj(t)-Xij(t)) (4)
其中,i表示第i个粒子,j表示粒子的第j维,V表示粒子的速度,t为当前迭代次数,X表示粒子的位置,P为粒子的个体最好位置,G为粒子群全局最优位置,C为粒子群平均最优位置,w被称为惯性权重,c1,c2,c3为加速系数,r1,r2,r3为[0,1]之间均匀分布的随机数。
粒子的位置更新公式如下:
Xij(t+1)=Xij(t)+Vij(t+1) (3)
采用柯西变异算子更新粒子个体最优位置和外部档案具体为:
比较新粒子与粒子个体最优位置的Pareto支配关系,若支配,则用新粒子替代个体最优位置,若被支配,则利用柯西变异算子对粒子进行扰动,对位置超出情况作极值处理,具体操作如下:
Cauchy(0,1)=tan((rand-0.5)×π) (5)
其中,X表示粒子的位置,i表示第i个粒子,j表示粒子的第j维,Cauchy(0,1)为标准柯西分布产生的随机数,rand为[0,1]之间均匀分布的随机数。pb为变异概率,定义如下:
其中,t为当前迭代次数,MaxIt为总迭代次数。
所述方法具体包括以下步骤:
步骤1:设定所述方法的基本参数,随机初始化粒子的速度和位置;
步骤2:根据粒子之间的Pareto支配关系初始化外部档案;
步骤3:计算外部档案中粒子的拥挤距离并对粒子进行排序,分别为每个粒子随机选择全局最优位置;
步骤4:根据式(2)和(3)更新粒子的速度和位置;
步骤5:利用柯西变异算子更新粒子个体的最优位置和外部档案;
步骤6:当外部档案中粒子数达到最大设定限度时,采用拥挤距离排序策略维护外部档案;
步骤7:判断当前迭代次数是否达到最大迭代次数,若达到,则将外部档案中粒子作为最终的Pareto最优解集输出,否则,转到步骤3。
实施例2
在本实施例中使用实施例1中所述方法,对多目标测试函数进行测试;选择ZDT测试函数集的5个典型的多目标测试函数ZDT1,ZDT2,ZDT3,ZDT4和ZDT6进行测试。测试函数具体形式如表1所示。其中,ZDT1的Pareto前沿是凸的,ZDT2的Pareto前沿是非凸的,ZDT3的Pareto前沿是由5段非连续的凸区域组成,ZDT4的Pareto前沿具有219个局部最优,主要测试本实施例中所述方法求解多峰问题的能力,ZDT6具有非凸且非均匀的Pareto前沿,用来测试算法保持种群多样性的能力。以上实验测试函数能从非凸性、非均匀性、非连续性以及多峰性等方面综合测试多目标优化算法的优劣。
表1实验中的测试函数
本文选择错误率ER(Error Ratio)、世代距离GD(Generational Distance)、拥挤方差CV(Crowding Variance)和运行时间CT(Computational Time)四个指标来定量评价所提多目标优化算法的准确性、多样性、分布性和运算速度。粒子群规模为100,最大迭代次数为200,外部档案大小设置为100。将本发明所述方法,即MOPSO-SCM算法,与NSGA-II、MOPSO-CD、MOQPSO-CD三种典型多目标优化算法进行对比分析。仿真是在酷睿CPU 3.30GHz,4GB RAM计算机上的Matlab2013实验环境下进行。每种算法对于每一个测试函数都独立运行30次,并分别统计实验结果。
四种算法对5个测试函数某一次优化得到的Pareto前沿如图2~图21所示。从仿真图可以看出,MOPSO-SCM和MOQPSO-CD算法对ZDT测试函数集都能得到较好的Pareto前沿,对于非凸非均匀的ZDT6测试函数,MOPSO-SCM的求解效果更佳。四种算法对每一个测试函数独立运行30次并统计平均结果如表2所示。性能评价指标错误率ER的优先级最高,其次是世代距离GD和拥挤方差CV,算法消耗时间CT优先级最低。
表2四种算法对ZDT测试函数的性能指标
四种算法中MOPSO-SCM算法的错误率最低(ER值最小),收敛精度高(GD值小),分布性好(CV值小),运算速度最快(CT值最小)。
将共享学习因子引入粒子速度更新公式,采用柯西变异算子更新粒子个体最优位置和外部档案,提高了多目标粒子群优化算法的收敛精度和多样性,并提高了算法的运行效率。为解决实际工程中的多目标优化问题提供了一种新的方法。
- 还没有人留言评论。精彩留言会获得点赞!