用于分析离港值机旅客排队的数据处理方法及装置与流程

本发明涉及数据处理
技术领域：
，具体涉及一种用于分析离港值机旅客排队的数据处理方法及装置。
背景技术：
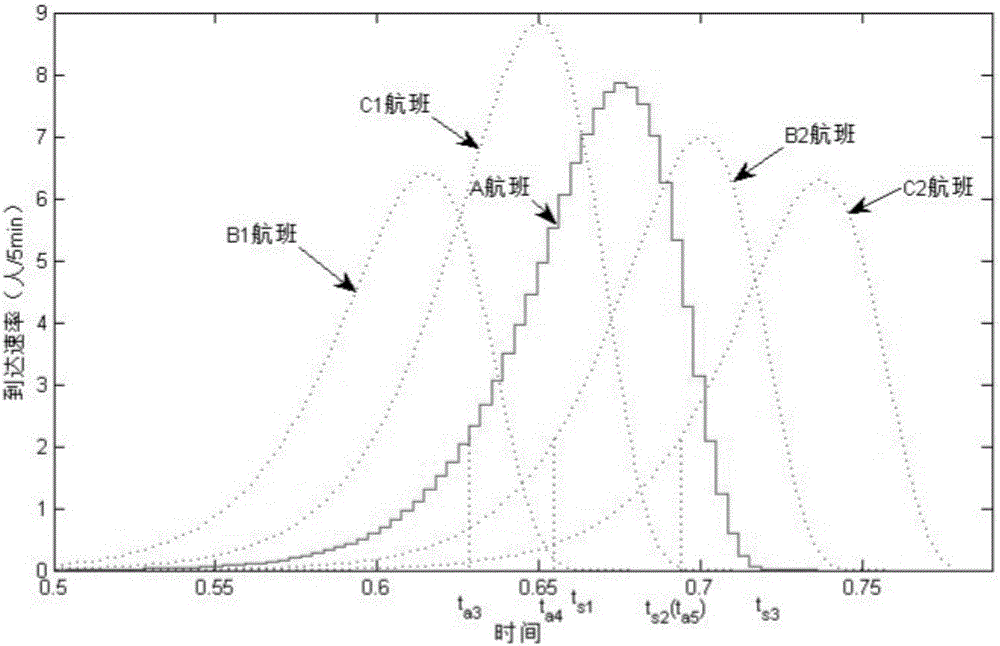
：目前，庞大的旅客流量导致国内各机场服务资源紧张，以某枢纽机场为例，其面向旅客服务的PKI指标(旅客值机服务时间等)高达75％的不合格率，这给机场运行带来了极大挑战。巨大的客流量是造成上述问题的主要原因，因此如何通过客流预测实现资源优化调度，提高机场运行效率，是解决上述问题的关键。旅客值机排队长度作为航站楼内旅客聚集以及机场运行效率的直观反映，直接关系到过站等待时间。如果能够得到旅客值机排队长度的高精度预测结果，就可为值机柜台的优化分配策略提供依据，因此，如何准确预测旅客值机排队长度变化就成为首要解决的关键问题。排队问题的研究已经在交通运输领域展开，关于队列长度预测方法也已经在交通运输领域开始应用。例如，假设绿灯时车辆等间隔离开，通过离散到达过程(如泊松分布)得到了车辆排队长度和延迟的概率母函数，并基此得到整个排队长度和延迟分布；又如，通过在过饱和的交通状况下建立实时分区，来检测连续链接的关键集群，并通过在每个集群的最上游和下游的路口建立局部较小型的分散信号控制策略，从而实现实时的自适应交通信号控制，改善车辆排队倒流阻塞的问题。车辆位置和时间数据获取方式通常在十字路口安放监测装置或监测车辆，并通过移动传感器采集路口车辆通过时间数据，首先定义了队尾不延迟到达时间的概念，并基此估计一个周期内最大和最小队长，最终得到了实时队列长度的曲线；另外，通过使用探测车辆在十字路口采集的数据，基于条件概率分布建立了用于估算预期队长及其变化的解析公式，也能够建立溢出队列情况下的近似模型。但是，以上在交通运输领域的研究所用数据都是来源于监控设备实时采集，只能根据当前实时数据预测即将产生的排队变化，并不能基于往期历史数据产生规律性的到达率曲线，因此数据的使用具有很大局限性，且提前预估性较差。技术实现要素：针对现有技术中的缺陷，本发明提供一种用于分析离港值机旅客排队的数据处理方法及装置，以解决无法根据往期历史数据预测即将产生的排队的问题。一种用于分析离港值机旅客排队的数据处理方法，包括：确定值机柜台的值机排队聚集速率；根据所述值机排队聚集速率，并通过叠加运算和递推算法确定变化时序下邻近多航班的值机排队长度模型；根据所述值机排队长度模型预测所述机场柜台的值机排队情况；根据所述值机排队情况对值机流程进行优化处理。一种用于分析离港值机旅客排队的数据处理装置，包括：第一数据处理模块，用于确定值机柜台的值机排队聚集速率；第二数据处理模块，用于根据所述值机排队聚集速率，并通过叠加运算和递推算法确定变化时序下邻近多航班的值机排队长度模型；数据预测模块，用于根据所述值机排队长度模型预测所述机场柜台的值机排队情况；数据处理模块，用于根据所述值机排队情况对值机流程进行优化处理。由上述技术方案可知，本发明提供的用于分析离港值机旅客排队的数据处理方法及装置针对国内非全开放式人工值机的业务场景，分析了国内离港旅客值机排队整个过程的聚集特性，并通过引入时序的概念对排队做离散化研究，针对国内离港旅客建立了邻近多航班的值机排队长度模型，通过该值机排队长度模型和排队论模型的对比实验，利用反证法分析每个离散时序内旅客的聚集速率特性，从而实现根据往期历史数据预测即将产生的排队。附图说明为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍。在所有附图中，类似的元件或部分一般由类似的附图标记标识。附图中，各元件或部分并不一定按照实际的比例绘制。图1示出了本发明提出的用于分析离港值机旅客排队的数据处理方法的流程图；图2示出了本发明提出的A航班与邻近航班的值机旅客聚集速率示意图；图3示出了本发明提出的排队长度对比图；图4示出了本发明提出的Li相对于的偏离度示意图；图5示出了本发明提出的用于分析离港值机旅客排队的数据处理装置的结构图。具体实施方式下面将结合附图对本发明技术方案的实施例进行详细的描述。以下实施例仅用于更加清楚地说明本发明的技术方案，因此只是作为示例，而不能以此来限制本发明的保护范围。需要注意的是，除非另有说明，本申请使用的技术术语或者科学术语应当为本发明所属领域技术人员所理解的通常意义。在本领域的现有技术中，在交通运输领域的研究所用数据都是来源于监控设备实时采集，只能根据当前实时数据预测即将产生的排队变化，并不能基于往期历史数据产生规律性的到达率曲线，因此数据的使用具有很大局限性，且提前预估性较差。而本申请的申请人在结合人类行为动力学研究中发现，航站楼旅客聚集规律由航班计划离港时刻主导，因此可通过航站楼旅客聚集模型高精度预测到旅客达速率，使得提前预估性有很大提高。人类动力学(Thedynamicsofhumanbehaviors)是研究人类的个体和群体行为的统计特性以及这些统计特性的产生机制和对社会、生态、经济、技术等各类外部系统所产生的效应的一门科学。人类动力学有关人类行为研究发现，受截止时间、个人喜好、排队优先权等因素的影响，人类的日常通信、浏览网站、图书借阅等行为呈现非泊松统计特性，而服从重尾分布。而航站楼内旅客的聚集行为在群体层面受截止时间影响服从对数正态分布特点的重尾分布，并且存在混合分布特性。进一步研究发现，人类行为动力学可较好刻画旅客值机排队的排队聚集速率分布。因此，本申请的申请人提出一种用于分析离港值机旅客排队的数据处理方法，结合图1所示，包括：步骤S11，确定值机柜台的值机排队聚集速率。可选的，该值机排队聚集速率包括单位时间内在值机队列的队尾聚集的旅客人数，该值机排队聚集速率与旅客在对应值机区的聚集速率之间的关系通过以下计算式确定：λ(t)=0,t<taQa,t=taρ(t),t>ta]]>其中，λ(t)表示值机排队聚集速率，Qa表示提前等待值机的旅客数，ρ(t)表示旅客在对应值机区的聚集速率，t表示值机开放时段内的时间，ta表示开始值机的时间。步骤S12，根据值机排队聚集速率，并通过叠加运算和递推算法确定变化时序下邻近多航班的值机排队长度模型。可选的，变化时序下邻近多航班的值机排队长度模型通过以下计算式确定：Li=L0+Σi=1i(λi-Nμi),1≤i≤is]]>其中，Li表示值机排队长度，L0表示初始值机排队长度，λi表示第i个时序下的值机排队聚集速率，i表示自然数，N表示值机柜台的数量，μi表示每个值机柜台的平均服务速率。在一可选实施例中，第i个时序内的值机排队聚集速率通过以下计算式确定：λi=Σjλij]]>ρij＝Qj(i)-Qj(i-1),1≤i≤is其中，λi表示第i个时序内的值机排队聚集速率，λij表示第i个时序内j航班旅客在对应值机区的值机排队聚集速率，ρ1j表示第1个时序内j航班旅客在对应值机区的聚集速率，ρij表示第i个时序内j航班旅客在对应值机区的聚集速率，Qj表示航班在第i时序的抽样时刻已经抵达值机区的旅客数量。在一可选实施例中，单值机柜台平均服务速率通过以下计算式确定：μi=λiN,Li-1+λi<Nμmaxμmax,Li-1+λi≥Nμmax]]>其中，Li-1表示第i-1时序的排队长度，N表示开放的值机柜台的数量，μmax表示每个时序的间隔内平均单个值机柜台的最大服务速率。步骤S13，根据值机排队长度模型预测机场柜台的值机排队情况。其中，根据值机排队长度模型，可在任意时刻预测任意机场柜台的值机排队情况。例如，某一时刻机场柜台的值机排队情况已经超过阈值，而在下一时刻该机场柜台的值机排队情况又小于阈值，则能够说明排队情况的变化。步骤S14，根据值机排队情况对值机流程进行优化处理。其中，根据值机排队情况可对值机流程进行相应的优化处理。例如，某一时刻机场柜台的值机排队情况已经超过阈值，说明此时刻的机场柜台处理能力已经无法满足值机要求，应当增加开放的值机柜台数量；在若干个时刻后，机场柜台的值机排队情况变为小于阈值，说明此时刻的机场柜台处理能力已经超过值机要求，应当减少开放的值机柜台数量。采用本实施例提出的用于分析离港值机旅客排队的数据处理方法，针对国内非全开放式人工值机的业务场景，分析了国内离港旅客值机排队整个过程的聚集特性，并通过引入时序的概念对排队做离散化研究，针对国内离港旅客建立了邻近多航班的值机排队长度模型，通过该值机排队长度模型和排队论模型的对比实验，利用反证法分析每个离散时序内旅客的聚集速率特性，从而实现根据往期历史数据预测即将产生的排队。下面通过具体的实施例对本发明提出的用于分析离港值机旅客排队的数据处理方法进行详细说明。由于旅客的值机排队聚集规律并不等同于旅客在对应值机区的聚集规律，因此本步骤分析了单航班旅客在对应值机区的聚集规律，然后通过建立了旅客值机排队聚集速率与在对应值机区聚集速率的关系，得到了单航班值机排队聚集速率的特性。首先，确定单航班旅客在值机区的聚集规律。抵达航站楼的旅客有如下特性：是否需要人工值机是随机的以及需值机的旅客会优先去值机。由以上两个特性可知，单航班旅客在航站楼的聚集规律与在对应值机区域的聚集规律相同。申请人通过结合人类行为动力学对航站楼旅客的聚集过程进行了研究，发现单航班旅客在航站楼的聚集规律服从对数正态分布特点的重尾分布，因此单航班旅客在对应值机区的聚集规律也可按对数正态分布特点的重尾分布考虑。其次，确定单航班旅客的值机排队聚集规律。旅客到达值机区并不一定直接排进队中，而是等到开始值机以后才会迅速排入队中，且此时已经有相当比例的旅客在提前等待值机。申请人提出定义1：单位时间内在值机队列的队尾聚集的旅客人数定义为值机排队聚集速率(TheDistributionofqueuingaggregationrate)。设某航班人工值机旅客在对应值机区的聚集速率为ρ(t)，值机排队聚集速率为λ(t)，值机开放时段内的时间为t，开始值机的时间为ta，提前等待值机的旅客数为Qa，在非全开放的值机方式以及蛇形队排队方式下，通过以上旅客值机排队的特点可得到λ(t)与ρ(t)的如下关系：λ(t)=0,t<taQa,t=taρ(t),t>ta---(1)]]>t＝ta时开始值机，提前聚集的等待值机的旅客会迅速排入队中，使得排队聚集速率发生突变，突变量为Qa，如同泄洪，将值机排队中的这一特点称为“泄洪效应”(Flood-dischargeEffect)。t>ta时，有λ(t)＝ρ(t)，结合人类行为动力学的分析，可知值机开始(突变点)以后的排队聚集速率λ(t)也服从对数正态分布特点的重尾分布规律。因此，在非全开放的值机方式以及蛇形队排队方式下，就单航班旅客值机排队的整个聚集过程而言，在值机刚开始时会有“泄洪效应”发生，之后服从对数正态分布特点的重尾分布规律。实际场景中，多个临近航班总的聚集过程是对以上排队聚集过程的叠加。根据以上值机排队聚集速率λ(t)的特性，已知开始值机以后的旅客排队到达规律服从对数正态分布，假设每个值机柜台服务能力相同，直接从排队形成原理入手，先引入时序的概念，然后通过叠加运算和递推算法得到变化时序下邻近多航班的值机排队长度模型(Check-inQueueLengthModelofMultipleAdjacentFlights，MAF-CQLM)。首先，确定旅客聚集速率的离散化。以某个参考航班整个开放值机的时段为基准，研究这段时间内与该航班值机时间有交叉的临近航班，这些航班的旅客在值机时排在同一条蛇形队中。一般截止值机的时间为航班预计离港时刻前30min，假设值机持续时间为两小时。受旅客到达不连续的限制，无法得到时间上连续的排队长度，首先需要对旅客聚集速率做离散化处理，因此我们引入时序的概念。申请人提出定义2：设t是某航班值机开放期间内的时刻，ta和ts分别为该航班开始值机的时间和截止值机的时间。将ta到ts的时段平均分为若干个长度为tp(min)的小时段，tp取值范围是1min≤tp≤10min，定义每个小时段称为时序段，简称时序(Timeseries)。用i表示时序号，i的表达式为：i=t-tatp,ta+tp≤t≤ts---(2)]]>t的取值应保证使i为整数。为了能够尽可能反映队列长度变化的实时性，tp不宜取值过大，且也不宜取值过小，因此本实施例可选tp取值范围在1min到10min之间。引入时序的定义以后，可以对聚集速率做离散化处理。下面给出在时序概念下的聚集速率的定义。申请人提出定义3：设γ是某个航班的值机旅客在时间为tp的单个时序内聚集的人数，定义γ为该航班的聚集速率(Aggregationrate)。聚集速率包括值机区聚集速率和值机排队聚集速率。用ρij和λij分别代表第i时序内j航班旅客在值机区域的聚集速率和值机排队聚集速率，则二者在时序定义下有如下一般关系：其中，l0j表示j航班开始值机前已经到达的旅客数量(突变量)，假设这些旅客会在第一个时序内迅速排进队中，即“泄洪效应”(Flood-dischargeEffect)对应于i＝1的时序；is为截止值机的时间ts对应的时序号。若某参考航班有多个邻近航班，那么对该参考航班的值机时段进行时序划分，并以此时序为基准，给出以下单个时序内的混合排队聚集速率的定义。申请人提出定义4：设λ为单个时序内总的值机排队聚集速率，即λ等于该时序内涉及的所有航班的旅客排队聚集速率的叠加，称λ为混合排队聚集速率(Mixedqueuingaggregationrate)。若用λi表示第i个时序内的混合排队聚集速率，λi有如下表达式：λi=Σjλij---(4)]]>其中，j为参考航班值机时段内涉及的航班，包括参考航班在内，按照值机开始的先后顺序排列有j＝1，2，3，……。其次，确定值机排队长度模型。引入时序概念以后，将整个值机排队的过程做离散化研究，根据值机排队聚集速率λ(t)的特性，可以得到计算值机排队长度的模型。经离散化处理后的邻近多航班旅客值机排队长度是按照时序变化的，下一时序的排队长度是在当前时序排队长度基础上发生改变，即排队长度变化具有无后效性。如果已知开始值机时候的初始排队长度，那么利用排队长度变化的无后效性可以计算整个值机时段内排队长度的变化情况。假设在第i时序内每个值机柜台对旅客的平均服务速率为μi，值机柜台数为N，初始排队长度为L0，那么第i时序采样时刻的值机旅客排队长度Li的表达式为：Li=L0+Σi=1i(λi-Nμi),1≤i≤is---(5)]]>这样邻近多航班离港旅客值机排队长度模型(MAF-CQLM)可通过以下简式表示：Li＝Li-1+ΔLi,1≤i≤is(6)且有ΔLi＝λi-Nμi(7)其中λi由上述的定义3确定，即：λi=Σjλij]]>通过式(6)可以得到以下性质：性质1：MAF-CQLM模型具有马尔科夫性(Markovproperty)。证明包括：设值机开放的时段为T，每个Li对应一个状态xi，状态空间为S＝{X(t),t∈T}。由式(6)可知，对于有在条件X(ti)＝xi，xi∈S，i＝1,2,…,i-1下，状态xi仅是xi-1的函数关系式，那么状态xi对于过去状态的条件概率分布仅是xi-1的函数，即有P(xi＝x|x1,x2...,xi-1)＝P(xi＝x|xi-1)因此MAF-CQLM模型具有马尔科夫性。通过MAF-CQLM模型的形式可以发现，其本质上是累计曲线法的数学表达式。MAF-CQLM模型使用时不受泊松分布聚集规律的限制，理论上有更好的适应性(Suitability)。适应性(Suitability)在离散时序中的定义如下:申请人提出定义5：以每个时序间隔为单位时间，将计算每个时序的排队长度的能力定义为适应性(Suitability)。若设p为能够计算出排队长度的时序所占的比例，那么p越大代表适应性(Suitability)越好，反之越差。最后，确定MAF-CQLM模型变量。若要比较准确地预测排队长度的变化情况，需要选取可高精度预测的旅客聚集速率模型。作者前期已经建立的TD-SFAPM模型预测精度高达80％以上，较一般同类模型有更高的预测精度，因此本实施例选用TD-SFAPM模型计算旅客值机排队的聚集速率λi，并对TD-SFAPM模型作如下变形：Q(t0-t)＝S*p(t0-t)(8)t0表示航班预计起飞时间，t表示值机开放时段内的时间，S表示该航班经济舱旅客需要办理人工值机的总人数。Q和p是t的函数，其中Q代表距离航班起飞时间t0-t的时刻已到达的经济舱人工值机旅客数；p代表距离航班起飞时间t0-t的时刻已到达人工值机区的旅客比例，且有：p(t0-t)=12-12erf[ln(t0-t)-αβ2]---(9)]]>其中参数α和β由离港航班时刻t_0唯一决定，有:α=43.68t04-95.04t03+71.64t02-21.29t0-0.7403]]>β=2.44t03-4.738t02+3.179t0-0.383]]>设taj为j航班开始值机的时间，通过TD-SFAPM模型可以计算taj时候已经等待值机的j航班旅客数(突变量)，即l0j。l0j的表达式如下：l0j＝Qj(t0-taj)(10)其中Qj表示j航班的TD-SFAPM模型。j航班的值机旅客在第i时序内的排队到达速率可以通过以下式子计算：ρij＝Qj(i)-Qj(i-1),1≤i≤is(11)其中Qj(i)表示j航班在第i时序的抽样时刻已经抵达值机区的旅客数，有Qj(i)＝Qj(t0-tij)且Qj(0)＝l0j。通过式(11)可计算式(3)中j航班旅客的值机排队聚集速率λij，进而通过定义4求解总的排队聚集速率λi。另外，μi是随着旅客到达速率以及柜台开放数量变化而变化的，因此首先需要得到繁忙状态下平均每个值机柜台的最大服务速率，然后通过第i时序的服务繁忙程度确定μi。依据陆迅等统计研究，综合考虑值机旅客携带行李的数量，假设每个值机柜台对旅客的服务能力相当，可计算出平均服务每位旅客的时间约为52秒。考虑到离队到值机柜台的行走时间不可忽略，可取离队到服务完成的整个过程平均时间为58秒。通过计算可得到每个时序的tp间隔内平均单个值机柜台的最大服务速率μmax，有：μmax=60*tp58---(12)]]>申请人提出定义6：设第i-1时序的排队长度为Li-1，第i时序内总的排队聚集速率为λi，开放值机柜台数量为N，若Li-1+λi≥Nμmax，则称第i时序繁忙(busy)；若Li-1+λi<Nμmax，则称第i时序为不繁忙(notbusy)。通过值机柜台的繁忙度(繁忙或不繁忙)确定μi，有：μi=λiN,Li-1+λi<Nμmaxμmax,Li-1+λi≥Nμmax---(13)]]>通过以上对MAF-CQLM模型中的变量λi和变量μi的确定可实现模型的计算。依据国内某航空公司某日的航班数据，随机选取一个航班作为参考航班，假设该参考航班为A航班，如图2所示，其值机开放时段为15:35到17:35，对该值机时段做时序划分，任意取一个满足定义1条件的tp值，此处取tp＝6min。从A航班的临近航班中随机选取4个航班，并与A航班按照值机开始的先后顺序依次排列为B1航班、C1航班、A航班、B2航班、C2航班，依次对应j＝1,2,3,4,5，如图2所示，计划起飞时间记为t0j，开始值机的时刻记为taj，截止值机的时刻记为tsj。表1中给出了以上5个航班的参数值，其中用Sj表示j航班的人工值机总人数。表1表2为时间归一化处理后的各航班参数。表2本实施例利用MAF-CQLM模型与常用的多服务窗等待制排队模型M/M/n(简称M/M/n排队模型)分别对以上数据进行值机排队长度的计算，并利用反证法对各离散时序内的聚集规律分析。设置对比实验时，两个模型使用相同的到达速率和服务速率。M/M/n排队模型需假设值机旅客在每个满足λ<Nμ的关系的时序内都以泊松流到达，且各服务柜台服务时间服从负指数分布，而MAF-CQLM模型无此前提假设，通过对比两模型的计算结果的差异性，可确定此假设的正确性。值机柜台开放的数量N和初始排队长度l0会影响到排队长度的变化，实验中假定N＝3，l0＝0，并通过式(12)计算出单个值机柜台平均最大服务速率μmax为6.2人/(6min)，这样可以得到从时序1到时序20所对应的各个抽样时刻的排队长度，实验结果如表3所示。表3表3中Li和分别表示MAF-CQLM模型计算的队长(取整以后)以及M/M/n排队模型计算的平均队长(取整以后)，λi表示预测的第i时序总排队聚集速率，μi表示第i时序单柜台平均服务速率。通过表3中两个模型计算结果，可以发现二者的计算结果差异比较明显。首先，MAF-CQLM模型计算结果比较完整，而M/M/n排队模型计算结果不完整。这是因为M/M/n模型不能计算非稳态的时序，即λi>Nμi的时序。而MAF-CQLM模型使用时不受泊松分布聚集规律的限制，可用于稳态时序和非稳态时序的计算，因此计算结果的完整度(Integrity)好。由上述定义5可知，计算结果的完整度(Integrity)可以反应出模型适应性(Suitability)的好坏。分别用pMAF和pMMn表示MAF-CQLM模型和M/M/n排队模型的完整度，因为MAF-CQLM模型可以计算每个时序的排队长度，所以理论上pMAF＝100％；而M/M/n排队模型只能在满足稳定条件的时序计算排队长度，因此理论上pMMn≤100％。本次实验中可用于M/M/n排队模型计算的时序有13个，有pMMn＝65％<pMAF＝100％，所以MAF-CQLM模型具有更好的适应性(Suitability)。其次，在满足λi>Nμi条件的稳态时序内的计算结果也相差较大，图3中给出了MAF-CQLM模型和M/M/n模型计算的排队长度随时序变化的图像，以及他们的误差绝对值，即的值。由图3可以看到，稳定时序内两模型的计算结果最大时相差26人。如果用ω表示相对于Li的偏离度(Deviation)，可得到图4。由图4可以看出，13个稳定时序中有10个时序偏离度超过了40％，占比达77％，甚至在第2、3时序偏离度超过100％。通过以上完整度(Integrity)和偏离度(Deviation)的指标对比，证明各时序内旅客值机排队的聚集规律λi服从泊松分布的假设不正确。进一步分析，由于旅客在值机区的聚集速率ρ受航班离港时刻的影响，那么由λi和ρi的关系式(3)可知，λi也受航班离港时刻影响。此外，λi还会受到“泄洪效应”(Flood-dischargeEffect)的影响，在刚开始值机的时序会发生突变，因此，旅客值机排队的聚集规律在离散时序内受航班离港时刻和值机开始的时间影响，呈非泊松分布的特点。从MAF-CQLM模型计算结果看，A航班、B2航班和C2航班开始值机的时序(第1时序、7时序和15时序)内排队长度都发生了排队人数突然增大的现象，这正是由“泄洪效应”(Flood-dischargeEffect)造成的。另外可以看到，在开放3个值机柜台的时候，最大的排队人数将达到53人，且出现在第15时序内，即16:30到16:35之间。本发明的具体实施方式还提出了一种用于分析离港值机旅客排队的数据处理装置，如图5所示，包括：第一数据处理模块101，用于确定值机柜台的值机排队聚集速率；第二数据处理模块102，用于根据所述值机排队聚集速率，并通过叠加运算和递推算法确定变化时序下邻近多航班的值机排队长度模型；数据预测模块103，用于根据所述值机排队长度模型预测所述机场柜台的值机排队情况；数据处理模块104，用于根据所述值机排队情况对值机流程进行优化处理。可选的，第一数据处理模块101具体用于：通过以下计算式确定所述值机排队聚集速率与旅客在对应值机区的聚集速率之间的关系，其中所述值机排队聚集速率包括单位时间内在值机队列的队尾聚集的旅客人数：λ(t)=0,t<taQa,t=taρ(t),t>ta]]>其中，λ(t)表示值机排队聚集速率，Qa表示提前等待值机的旅客数，ρ(t)表示旅客在对应值机区的聚集速率，t表示值机开放时段内的时间，ta表示开始值机的时间。可选的，第二数据处理模块102具体用于：通过以下计算式确定所述变化时序下邻近多航班的值机排队长度模型：Li=L0+Σi=1i(λi-Nμi),1≤i≤is]]>其中，Li表示值机排队长度，L0表示初始值机排队长度，λi表示第i个时序下的值机排队聚集速率，i表示自然数，N表示值机柜台的数量，μi表示每个值机柜台的平均服务速率。在一可选实施例中，第二数据处理模块102还具体用于：通过以下计算式确定所述第i个时序内的值机排队聚集速率：λi=Σjλij]]>ρij＝Qj(i)-Qj(i-1),1≤i≤is其中，λi表示第i个时序内的值机排队聚集速率，λij表示第i个时序内j航班旅客在对应值机区的值机排队聚集速率，ρ1j表示第1个时序内j航班旅客在对应值机区的聚集速率，ρij表示第i个时序内j航班旅客在对应值机区的聚集速率，Qj表示航班在第i时序的抽样时刻已经抵达值机区的旅客数量。在一可选实施例中，第二数据处理模块102还具体用于：通过以下计算式确定所述单值机柜台平均服务速率：μi=λiN,Li-1+λi<Nμmaxμmax,Li-1+λi≥Nμmax]]>其中，Li-1表示第i-1时序的排队长度，N表示开放的值机柜台的数量，μmax表示每个时序的间隔内平均单个值机柜台的最大服务速率。采用本实施例提出的用于分析离港值机旅客排队的数据处理装置，针对国内非全开放式人工值机的业务场景，分析了国内离港旅客值机排队整个过程的聚集特性，并通过引入时序的概念对排队做离散化研究，针对国内离港旅客建立了邻近多航班的值机排队长度模型，通过该值机排队长度模型和排队论模型的对比实验，利用反证法分析每个离散时序内旅客的聚集速率特性，从而实现根据往期历史数据预测即将产生的排队。最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。当前第1页1 2 3