一种基于快速聚类的混合检测器生成方法与流程

本发明涉及一种检测器生成方法。

背景技术：

基于大数据的分析和应用日益广泛，人工免疫系统作为一种高效的生物启发计算方法再次成为研究的热点，众多学者在人工免疫系统领域开发新的算法。AIS由生物免疫系统启发而来，借鉴免疫系统的功能和原理并应用于复杂问题的解决，是最早的人工免疫系统模型。否定选择算法(NSA：Negative selection algorithm)作为人工免疫中一种重要的算法，是由T细胞在胸腺中成熟的模型而来的。FORRESTS最初于1994年提出基于字符串的否定选择算法(NNSA)，但是受计算开销的影响，限制了应用。后来，许多应用问题可以在真实值空间中定义和研究，检测器和抗原的属性被归一化到N维实值范围，所以NSA演变出了实值形式即RNSA。RNSA典型的是在二维空间中表示，具有可视化的特点。但传统的RNSA采用半径固定的检测器，这种方式生成的检测器有很多黑洞，而且覆盖率不理想。为了解决传统RNSA黑洞普遍的情况，Zhou Ji等人提出了采用可变半径的V-detector算法，检测器的半径被定义为到自体集边缘的距离。该算法不仅减少了黑洞现象，而且减少了检测器的数量。已经有很多实验证明V-detector算法得到好的效果。

在很多论文中提到，基于模式识别算法的对象距离计算，因此算法主要的时间开销集中在距离的计算上。但是RNSA，V-detector算法都没有考虑从减少距离计算来提升算法的效率。在RNSA和V-detector算法的检测器生成过程中，候选的检测器(未成熟的检测器)在自我耐受的时候需要计算该检测器与全部训练数据的距离。因此，NSA算法过多的时间开销是检测器生成过程效率过低导致的。针对于自体检测器个数过多的问题，公茂果等人提出FtNSA算法，在检测器生成之后，以异常检测器为样本去生成半径可变的自体检测器，生成自体检测器的过程基本与生成异常检测器相同。显然FtNSA算法大大减少了自体检测器的个数，可以在检测阶段极大的提高检测效率，但是仍然存在以下三个方面的问题：

(1)异常检测器生成效率方面，与V-detector相差无几，故FtNSA算法仍然存在异常检测器生成效率过低的问题。

(2)V-detector和FtNSA算法都没有考虑检测器集合中每个检测器的贡献。检测器存在严重的重叠现象，有的检测器的贡献其实很小，是基本无用的检测器，如果仍然把这些检测器保留下来，会导致自体检测器生成阶段和检测阶段效率变低。

(3)不管是RNSA，V-detector或者是FtNSA，都对自体训练数据有严格的要求，对训练数据没有识别和验证能力，他们认为所给的训练数据全部都是正常的。在实际中，由于噪声的影响，总会有少量的异常样本存在于训练数据中，如果不把这些样本识别出来进行剔除，那么算法就会认为这些异常样本是正常的。也就是说，检测器检测器无法覆盖这些异常样本，这会导致检测率大大降低，显然这是不合适的。

总的来说，目前大多数的改进NSA算法都存在检测器生成效率低下，所需自体样本个数过多，检测器重叠严重且没有抗噪声能力等问题。

技术实现要素：

为了克服已有检测器生成方法的效率较低、重叠严重且没有抗噪声能力、误测率较高的不足,本发明提供了一种效率较高、有效减少重叠、抗噪声能力较好、误测率较低的基于快速聚类的混合检测器生成方法。

本发明解决其技术问题所采用的技术方案是：

一种基于快速聚类的混合检测器生成方法，所述生成方法包括以下步骤：

1)基于快速聚类算法实现划分，生成少量自体检测器替代自体样本，步骤如下：

1.1)对训练数据进行基于密度的聚类分析，过程如下：

1.1.1计算每一对自体数据集S中的数据的距离，按升序排列，并确定d_c；

1.1.2计算每一个S中数据对象的ρ、δ、γ，并进行归一化处理；

1.1.3取分割区间数，画出γ的概率分布图，找到第一个概率密度为0的区间号i，并且令j＝1；

1.1.4对于第j个区间，判断此区间是否形成尖峰。如果不是，跳转步骤1.1.7；

1.1.5如果j≤i，跳转步骤1.1.7；

1.1.6将落在第j个区间的数据对象加入聚类中心集合Cen；

1.1.7如果j＜200，j++并跳转步骤1.1.4；否则，退出；

1.1.8根据聚类中心划分每个数据对象，得到n个类簇，每个类簇集合记为C_i，i∈[1,n]；

1.2)剔除噪声样本和检测边界点；

1.3)生成自体检测器；

2)异常检测器生成过程，设置检测器半径下限以及重叠分析；

3)在检测中只扫描异常检测器而不去扫描个数更多的自体检测器，被异常检测器激活的对象都被认为是异常个数，没有被异常检测器激活的对象被认为是正常个体。

进一步，所述1.2)中，剔除噪声样本和检测边界点的过程如下：

1.2.1i＝1；

1.2.2对于第i个类簇，画出它的ρ分布图；

1.2.3在分割区间数n的归一化ρ密度分布图中，如果第一个区间的概率密度大于第二个区间的概率密度，那么总存在第一个波谷所在的区间i，这个区间的密度上限即为噪声密度阈值ρ_bⁱ；

在左半平面总存在一个概率密度最大的区间j，这个区间的密度下限即为边界密度阈值ρ_cⁱ；

1.2.3对于C_i中的每一个点，密度小于ρ_bⁱ标识为噪声，密度大于ρ_bⁱ而小于ρ_cⁱ标识为边界；

1.2.4如果i≥n，退出；否则i++，跳转步骤1.2.2。

再进一步，所述1.3)中，生成自体检测器的过程如下：

1.3.1i＝1；

1.3.2对于第i个类簇，以每一个不是噪声的点为圆心，R_s为固定半径生成自体检测器；

1.3.3获取第i个类簇的聚类中心，找到距离这个聚类中心最近的一个边界点，两者距离记为R_c，以聚类中心为圆心，R_c为自适应半径生成大自体检测器；

1.3.4检测出被大自体检测器包含的固定半径检测器，将它们剔除；

1.3.5对第i个类的自体检测器进行重叠分析，剔除无用自体检测器；

1.3.6如果i≥n，退出；否则i++，跳转步骤1.3.2。

更进一步，所述步骤2)中，用两个检测器中心的距离dis与两个检测器的半径R1，R2的关系来判断，通过(6)来判断它们是否重叠，若是满足(6)，则判断为重叠，ma为预设值；

dis＜R1+R2(ma-1) (6)。

所述步骤2)中，检测器半径下限取自体半径R_s。

本发明的技术构思为：设计了一种半径自适应的混合检测器生成算法FCA-MD(Mixed Detectors based on fast clustering algorithm)。

在调用检测器算法之前生成自体检测器，将自体个数降低，故检测器生成的算法被提高，这是FtNSA所欠缺的。另外，FCA-MD分析检测器集合的重叠，将无用检测器剔除，进一步降低自体检测器和异常检测器的个数。

FCA-MD的算法分为自体检测器生成算法FCA-SD、异常检测器生成算法V-ND和检测算法MD算法三个主要部分，分别如下：

1)自体检测器生成算法FCA-SD针对自体样本过多的问题，基于快速聚类算法实现划分，生成少量自体检测器替代自体样本，以此来提高检测器生成算法效率。参考了Alex Rodriguez和Alessandro Laio在Science期刊上发表的一种快速搜寻密度峰聚类方法(DPC)[15]，设计一种改进的DPC算法，提出一种自动确定聚类中心的新方法，通过找出多个合适的密度阈值来划分核心点、噪声点和边界点，再利用聚类中心与边界点生成半径自适应的自体检测器。

2)异常检测器生成算法V-ND实质上是对V-detector算法的改进，针对其检测器个数多、检测器质量不高的问题，设置了检测器半径下限以及重叠分析。

3)混合检测器MD为了实现更加快速可靠的检测，在检测中只扫描异常检测器而不去扫描个数更多的自体检测器。

FCA-MD的新特征有：(1)对实值自体集添加密度分布，并添加噪声，不再使用传统的均匀分布的数据集；(2)对密度数据集进行聚类分析，然后准确地识别噪声样本进行剔除并生成自体检测器；(3)在检测器生成的过程中，用自体检测器代替自体样本，并分析每个检测器的贡献，剔除重叠的无用检测器。

FCA-MD在检测器生成阶段做一个基于快速聚类的预处理，实现了自体样本的噪声剔除并生成半径自适应的自体检测器。通过用更少的自体检测器代替自体样本去生成异常检测器，大大提高检测器算法的效率。多组仿真实验验证了FCA-MD相比较于V-detector和FtNSA，可以在较少的自体个数下，获得更高的效率，更小的误测率以及更小的检测器集合。

本发明的有益效果主要表现在：效率较高、有效减少重叠、抗噪声能力较好、误测率较低。

附图说明

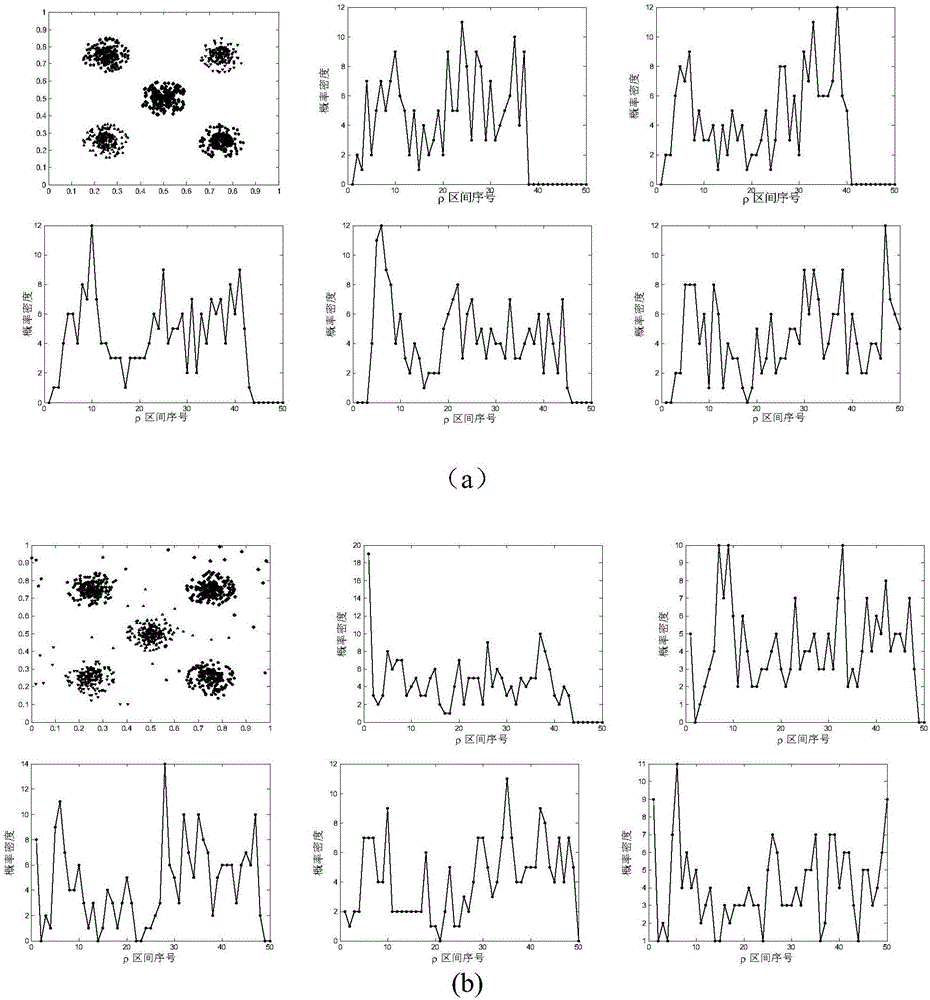
图1是Five Circle Data Set的典型γ概率分布图，其中，(a)是自体数据集分布图，(b)是γ分布图，(c)是聚类结果。

图2是Five Circle Data Set的ρ分布图，其中，(a)表示噪声比例0％的情况，(b)表示噪声比例5％的情况。

图3是噪声与边界的识别结果图。

图4是两种自体检测生成器效果比较，其中，(a)表示固定半径R_S自体检测器，(b)表示FCA-SD算法生成的自体检测器。

图5是重叠判定规则示意图，其中，(a)是重叠的情形；(b)是不重叠的情形。

图6是V-ND算法流程图。

图7是V-detector与V-ND算法生成的检测器对比图，其中，(a)表示V-detector算法；(b)表示V-ND算法。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图7，一种基于快速聚类的混合检测器生成方法，包括如下步骤：

1)自体检测器生成算法FCA-SD针对自体样本过多的问题，基于快速聚类算法实现划分，生成少量自体检测器替代自体样本，以此来提高检测器生成算法效率。参照文献1：R.Alex,L.Alessandro,Clustering by fast search and find of density peaks,Science,2014,344(6191):1492-1496。设计一种改进的DPC算法，提出一种自动确定聚类中心的新方法，通过找出多个合适的密度阈值来划分核心点、噪声点和边界点，再利用聚类中心与边界点生成半径自适应的自体检测器。

2)异常检测器生成算法V-ND实质上是对V-detector算法的改进，针对其检测器个数多、检测器质量不高的问题，设置了检测器半径下限以及重叠分析。

3)混合检测器MD为了实现更加快速可靠的检测，在检测中只扫描异常检测器而不去扫描个数更多的自体检测器。

FCA-SD算法包括：1.1)对训练数据进行基于密度的聚类分析；1.2)剔除噪声样本和检测边界点；1.3)生成自体检测器三个阶段。

参照文献1，运用DPC的ρ-δ的思想，基于γ的概率分布图找出聚类中心并准确划分；聚类中心的密度比周围的点高并且到密度更高的点距离十分远。利用这样的思想选出聚类中心，以它们为中心生成半径可变的自体检测器，达到将自体个体降低的目的。在此基本思想上，设计了一种聚类中心快速自动确定的快速搜寻密度峰聚类算法(DPC)，并基于DPC实现样本集的自体聚类和噪声点剔除。并且可以应用在不同形状和维度的数据集上。DPC的基本思想：

①聚类中心被密度小于它们的邻居所包围；

②聚类中心距离密度更高的点有相当大的距离。

即理想为了找到理想的聚类中心，DPC介绍了一个点的局部密度计算公式(1)和更高密度最邻近距离公式(2)。

这里需要说明的是，最高密度的点i的δ_i应该由(3)给出。可以看出，局部密度最大或者全局密度最大的点，其δ_i值比周围邻居的δ_i大很多。DPC搜寻这种δ_i异常大的点为密度峰，将其作为聚类中心，参数d_c的值由输入参数t决定。

在有些数据集中，每个点的密度估计可能会存在误差，严重的时候会影响算法的效果。为此，我们需要一种更加精确的密度计算公式(4)。

在DPC中，聚类中心可以通过对决策图分析得到，即δ_i和ρ_i都很大的点为聚类中心。但是，没有一个标准去评判多大δ_i和ρ_i的点可以作为聚类中心。在聚类中心并不明显时，DPC算法又提供一个思路，将γ_i＝ρ_iδ_i降序排列，截选去前N个点作为聚类中心。但是仍然不是一个自动的过程。根据思路，设计自动确定聚类中心的方法：对于任意数据集D，分别计算每一个数据点i的两个属性值：数据对象的局部密度和到具有更高局部密度的其他点的最小距离，从而根据γ_i＝ρ_iδ_i得到数据集D中每个数据点i的γ分布图，得到定理1。

定理1对于数据集D的所有数据点γ分布图，在第一个概率密度为0的区间之后，若存在这样的若干个区间，它的概率密度不为0且比相邻的两个区间大，则落在这些区间的数据被认为是聚类中心。

在计算每个点的γ_i后，将其进行归一化到[0,1]空间，然后将[0,1]分割成100个区间，计算γ_i落在每个区间的点个数，从而画出γ_i的概率分布图，分析概率分布图，在第一个概率密度为0的区间之后，若存在这样的若干个区间，它们都满足其概率密度不为0且比相邻的两个区间大，则落在这些区间的数据被认为是聚类中心。

假设取Five Circle Data Set数据为例，通过定理1计算获得相应区间的数据，并将其作为聚类中心，实际数据验证了定义1的有效性。

图1显示了一个Five Circle Data Set的典型γ概率分布图。图1(a)为数据集的显示，可以看出有密度分布的Five Circle Data Set理论上应该有5个聚类中心，图1(b)为其γ分布图，横轴为γ的区间数，第i个区间的γ范围为纵轴为γ落在这个区间的点的个数。从图1(b)可以看出，γ分布在第一个或第二个区间的点非常多，且随着区间数增加，概率密度急剧降为0。而在第一个密度为0的区间之后，形成几个尖峰，可以发现尖峰的数量与理论上聚类中心个数很接近。至此验证了定理1。

FCA-SD第一阶段为聚类分析，过程如下：

1.1.1计算每一对自体数据集S中的数据的距离，按升序排列，并确定d_c；

1.1.2计算每一个S中数据对象的ρ、δ、γ，并进行归一化处理；

1.1.3取分割区间数100，画出γ的概率分布图。找到第一个概率密度为0的区间号i，并且令j＝1；

1.1.4对于第j个区间，判断此区间是否形成尖峰。如果不是，跳转步骤1.1.7；

1.1.5如果j≤i，跳转步骤1.1.7；

1.1.6将落在第j个区间的数据对象加入聚类中心集合Cen；

1.1.7如果j＜200，j++并跳转步骤1.1.4；否则，退出；

1.1.8根据聚类中心划分每个数据对象，得到n个类簇，每个类簇集合记为C_i，i∈[1,n]。

FCA-SD通过这种方式，在γ分布图上检测尖峰来确定聚类中心。找到聚类中心后，运用DPC算法的思想进行分类；图1(c)显示了聚类的结果，不同点形表示不同的类簇。

FCA-SD只是利用聚类中心生成自体检测器，并不是做单纯的聚类，也没有聚类准确率这个指标，所以对聚类中心的个数没有严格的要求。如果FCA-SD在Five Circle Data Set中选出了6个聚类中心，这是不要紧的，因为这只是意味着多了一个自体检测器，并不是说分类不准确。

一种标识噪声与数据点边界的新方法，该阶段建立在聚类分析完成的基础上，基于每个类簇的ρ概率分布图找到多个合适的密度阈值划分噪声点与边界点；

DPC介绍了每个类簇的边界区域来剔除噪声。边界定义为这样的点集，点集里属于一个类簇的点在距离d_c之内存在着属于看另一个类簇的点。找出每个类簇的边界中密度最高的点，将其密度记录为ρ_b，即为噪声阈值。但是，当噪声的数量比较少，分属每个类簇的噪声之间的距离都大于截断距离时，每个类簇的ρ_b不能被计算。

定理2.在分割区间数n合适的归一化ρ密度分布图中，如果第一个区间的概率密度大于第二个区间的概率密度，那么总存在第一个波谷所在的区间i，这个区间的密度上限即为噪声密度阈值ρ_b，密度小于ρ_b的点为噪声。

定理3.在分割区间数n合适的归一化ρ密度分布图中，在左半平面总存在一个概率密度最大的区间j，这个区间的密度下限即为边界密度阈值ρ_c，密度介于ρ_b和ρ_c之间的点为边界点。

FCA-SD设计了一个新的判定噪声阈值的办法：把所有点的密度ρ归一化到[0，1]区间，将[0,1]合适地分割成k等分，与γ分布图相似，也画出每个类的ρ分布图。如果从第一个区间开始，单调递减过后出现的是第一个概率密度低谷，其所在区间号为m，将这个区间的密度上限作为该类的噪声阈值ρ_bⁱ，即该类中密度小于ρ_bⁱ的数据对象被认为是噪声。如果从第一个点开始单调递增过后出现的是第一个波峰，则该类的ρ_bⁱ为0。

以Five Circle Data Set为例。图2(a)显示了无噪声下Five Circle Data Set每个类的ρ分布图，图2(b)显示了5％噪声下Five Circle Data Set每个类的ρ分布图，第一个图为存在噪声的聚类结果图，分割区间数k均取50个。可以发现一个明显的区别：有噪声时，ρ分布图一开始呈下降的趋势且形成一个波谷，而无噪声时ρ分布图一开始从0增加到一个波峰。这就是由于噪声的密度与类簇中点的密度有一定的差距，即噪声的最大密度与类簇中点的最小密度有一定的间隔。如果我们适当的选择分割区间，就可以找到这个密度间隔，落在这个密度间隔内的点很少。因此，第一个波谷就把噪声与类簇区分开，这个波谷所在的密度区间的密度上限就作为了该类的密度阈值ρ_bi，每个类中密度小于这个阈值的点即为噪声。一般的，FCA-SD取分割区间数为50，对于噪声密度较高或较低的数据集，可以适当调整分割区间数以获得更加准确地噪声阈值。

在剔除噪声后，为了形成半径自适应自体检测器，需要去找出自体集的边界。在确定合适的分割区间数后，FCA-SD算法分析每个类的ρ分布图，从左半部分的波形图上找到最大尖峰值，即落在这个密度区间的点个数最多且大于相邻两个区间，这个区间的密度下限记为ρ_c。因为我们是从左半部分的波形中找的ρ_c，所以ρ_c∈[0,0.5]。FCA-SD将密度ρ_i满足ρ_b≤ρ_i≤ρ_c的点i作为边界点，它们在形成自体检测器中发挥作用。

FCA-SD第二阶段为噪声标识与边界检测，n为类簇个数，C_i为第i个类簇集合，i∈[1,n]，检测过程如下：

1.2.1i＝1；

1.2.2对于第i个类簇，画出它的ρ分布图；

1.2.3在分割区间数n的归一化ρ密度分布图中，如果第一个区间的概率密度大于第二个区间的概率密度，那么总存在第一个波谷所在的区间i，这个区间的密度上限即为噪声密度阈值ρ_bⁱ；

在左半平面总存在一个概率密度最大的区间j，这个区间的密度下限即为边界密度阈值ρ_cⁱ；

1.2.3对于C_i中的每一个点，密度小于ρ_bⁱ标识为噪声，密度大于ρ_bⁱ而小于ρ_cⁱ标识为边界；

1.2.4如果i≥n，退出；否则i++，跳转步骤1.2.2。

图3显示了在噪声比例5％下，噪声的剔除和边界检测的结果。黑点标识被剔除的噪声，在每个类簇中边界点用小圆点标识，边界以内的点用大圆点标识。可以看出，FCA-SD算法可以准确得剔除噪声并检测边界。

生成自体检测器阶段，采用自适应半径大检测器和固定半径小检测器结合的形式，生成个数少、覆盖域好的自体检测器。

标识出噪声和边界后，FCA-SD开始生成自体检测器。首先，我们以每个非噪声的点为圆心，生成半径为R_S(R_S为FCA-SD算法的输入参数，与V-detector和FtNSA算法中的自体半径一致)的固定半径自体检测器。这样生成的自体检测器是很多的，而且会出现重叠现象。然后，我们以聚类中心为圆心，以聚类中心到最近的边界点的距离为半径，生成一个大圆，并且将完全镶嵌在这个大圆里的无用常半径自体检测器剔除，这样就大大减少自体检测器的个数。但是，自体检测器还是存在一些重叠，是否重叠由公式(5)定义。

S_ij标志自体检测器i和自体检测器j是否被判定为重叠，c_i和c_j为两个自体检测器的中心。

当有两个自体检测器被判定为重叠时，只要选择其中一个剔除即可。

FCA-SD第三阶段为自体检测器生成，n为类簇个数，C_i为第i个类簇集合，i∈[1,n]，R_s为自体半径，过程如下：

1.3.1i＝1；

1.3.2对于第i个类簇，以每一个不是噪声的点为圆心，R_s为固定半径生成自体检测器；

1.3.3获取第i个类簇的聚类中心，找到距离这个聚类中心最近的一个边界点，两者距离记为R_c。以聚类中心为圆心，R_c为自适应半径生成大自体检测器；

1.3.4检测出被大自体检测器包含的固定半径检测器，将它们剔除；

1.3.5对第i个类的自体检测器进行重叠分析，剔除无用自体检测器；

1.3.6如果i≥n，退出；否则i++，跳转步骤1.3.2。

图4(a)说明采用固定半径的自体检测器，会导致大量重叠，尤其是在训练数据密度很高的区域内，自体检测器个数十分多，这在生成检测器阶段效率是很低的。图4(b)为FCA-SD算法生成的自体检测器，以聚类中心为圆心的大圆很好的覆盖了密度很高区域的自体检测器，使自体检测器大大减少。另外自体区域边缘的检测器个数也下降不少。图4说明了FCA-SD算法可以很好地将自体的个数降低，提高生成检测器的效率。

针对于V-detector算法检测器多且重叠严重的现象，V-ND算法对其进行了2个方面的改进：(1)增加重叠判断；(2)增加检测器半径下限。

判断两个检测器是否重叠，可以用两个检测器中心的距离dis与两个检测器的半径R1，R2的关系来判断。如图5(a)所示，两个检测器内切，满足dis＝R1-R2(这里我们假设R1大于R2)，显然这种情况是重叠的，检测器2是无用的检测器。如图5(b)所示，检测器2的中心在检测器1上，满足dis＝R1，但检测器2仍然有检测器1覆盖不到的空间，所以V-ND认为它们不重叠。若是检测器1与检测器2的dis满足R1-R2<dis<R1，我们通过(6)来判断它们是否重叠，若是满足(6)，则判断为重叠，ma为预设值，本发明取0.1。

dis＜R1+R2(ma-1) (6)

V-ND与V-detector算法仅有的不同为保存候选检测器的条件。V-ND算法在保存候选检测器时增加两个条件：1.检测器半径>R_s；2.利用重叠判定规则不与已有检测器重叠。如果不满足这两个条件，V-ND不会接受这个候选检测器，而是考虑其他更优良的候选检测器。图7表示V-detector与V-ND算法生成的检测器对比，一个黑圈代表一个检测器，黑圈覆盖的范围为检测器的覆盖区域。可以发现，V-detector算法检测器的覆盖域与V-ND算法检测器的覆盖域几乎一样，但前者的个数为500个，后者个数为164个，差不多是3倍左右，也就是说V-ND算法将检测器的个数降低了约67％。

设置检测器半径的下限主要是为了防止过小检测器的产生。一方面过小的检测器覆盖区域很小，即产生的贡献很小。另一方面，过小的检测器容易侵入自体区域，引起虚警率的提高。在本发明中，设置检测器半径下限为自体半径Rs。

检测算法MD为了追求检测效率，采用最简单，最快速的检测方案。在检测时只使用异常检测器，而不扫描自体检测器，只要是被异常检测器激活的对象都被认为是异常个数，没有被异常检测器激活的对象被认为是正常个体。