一种虚拟电厂热电联合调度鲁棒优化模型的利记博彩app

本发明属于电力系统电源调度领域，特别涉及一种虚拟电厂热电联合调度鲁棒优化模型。
背景技术：
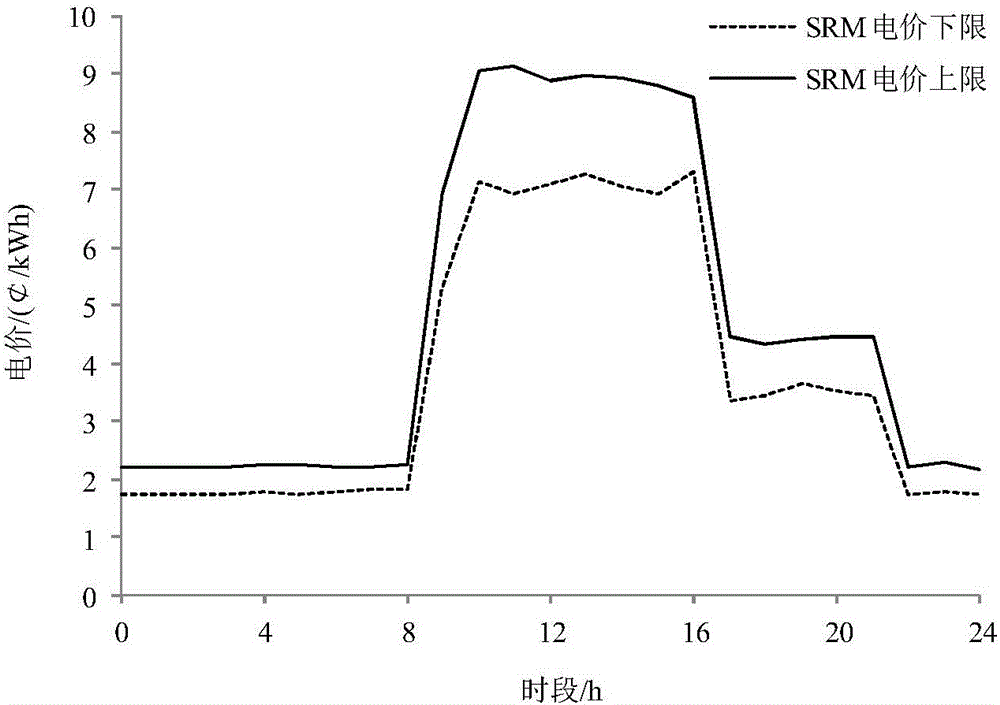
：近年来，热电联产(combinedheatandpower,CHP)机组以节能环保的优势蓬勃发展，但其发电和供热紧密联系的特点降低了其灵活性，因此，如何对其进行有效管理成为亟待解决的问题。虚拟电厂(virtualpowerplant，VPP)技术为解决该问题提供了新的思路。以VPP形式聚合CHP机组，通过能量管理系统控制其运行，能实现CHP机组乃至VPP整体的调度优化。VPP在调度过程中面临电价、可再生能源出力和负荷波动等多种不确定因素，给决策和系统安全运行带来很大的困难。因此，采用合理的调度方式，尽量量化或削弱不确定因素对调度策略的影响，实现利润最大化成为学术界研究的热点。鲁棒优化(robustoptimization，RO)作为一种处理不确定性的方法，具有无需知道不确定参数概率分布、计算快捷、规避风险能力好等优点。RO通过鲁棒系数调节系统的鲁棒性和经济性，鲁棒系数越大，系统鲁棒性越强，面临的风险越小。并且，现有研究多数考虑鲁棒系数对预期利润和决策方案的影响，极少涉及风险的定量分析，难免造成决策方案的保守或冒进，同时，也未面临RO处理SRM电价和热负荷不确定性的问题。技术实现要素：发明目的：提供了一种虚拟电厂热电联合调度鲁棒优化模型，解决同时参与能量市场(EM)和旋转备用市场(SRM)时，VPP日前热电联合调度优化模型建立问题。采用RO处理EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷的不确定性，降低VPP面临的风险，并建立风险量化指标，降低不确定性决策的盲目性。技术方案：本发明提供一种虚拟电厂热电联合调度鲁棒优化模型，包括以下步骤：步骤1：建立EM和SRM下VPP日前热电联合调度优化模型；步骤2：采用RO处理EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷的不确定性，建立RO模型；步骤3：建立风险量化指标，衡量系统面临的风险。进一步，步骤1包括以下步骤：对于VPP运营者而言，其目标为净利润最大化，因此优化模型的目标函数如下：maxΣt=1T(Ctm-Ctdg-Ctchp-Ctboil-Cts-Ctdr)]]>目标函数包含六个部分，分别为VPP参与电力市场所获利润DG成本CHP机组成本锅炉成本储能成本DR成本每部分具体表达式如下：Ctm=λtemPtem+λtsrmRtsrm]]>式中：分别为t时段EM电价和SRM电价；分别为t时段VPP在EM和SRM的竞标量，为决策变量。DG成本包括运行成本、启停成本和环境成本：Ctdg=Σi=1ni(kiPi,tdg+kifμi,to)+(λisuμi,tsu+λisdμi,tsd)+Pi,tdgΣe=1neQi,tdg(Ve+Ye)]]>式中：ni为DG单元数；为t时段第i单元DG输出功率，为决策变量；ki、为第i单元DG的燃料成本、固定成本、启动成本和停止成本；布尔变量分别表示t时段第i单元DG是否工作、启动、停止，是则置1，否则置0；ne为考虑的污染物总数；为第i单元DG第e项污染物排放量；Ve、Ye分别为第e项污染物环境价值、罚款数量级。CHP机组成本包括燃料成本、启停成本和环境成本，锅炉成本包括燃料成本和环境成本，本文考虑的CHP机组和锅炉均以天然气为燃料，如下式：Ctchp=Σl=1nl860λtngPl,techpHngηlchp+(λlsuμl,tsu+λlsdμl,tsd)+Pl,techpηlchpΣe=1neQl,echp(Ve+Ye)]]>Ctboil=Σk=1nk(860λtngPk,tboilHngηkboil+Pk,tboilηkboilΣe=1neQk,eboil(Ve+Ye))]]>式中：nl、nk分别为CHP机组和锅炉单元数；为t时段天然气价格；Hng为天然气热值；860为kWh转化为kcal的单位转换比率；为t时段第l单元CHP机组供电功率和第k单元锅炉供热功率，为决策变量；为第l单元CHP机组和第k单元锅炉效率，需要说明的是，仅为CHP机组的供电效率，并非整体效率；为第l单元CHP启动和停止成本；布尔变量分别表示t时段第l单元CHP是否启动、停止，是则置1，否则置0；为第l单元CHP机组和第k单元锅炉第e项污染物排放量，Ve、Ye分别为第e项污染物环境价值、罚款数量级；储能成本包括ES成本和TS成本，其与充、放电功率和储、放热功率近似呈线性关系：Cts=Σx=1nx(axes(Px,tesc+Px,tesd)+bxes)+Σz=1nz(azts(Pz,ttsc+Pz,ttsd)+bzts)]]>式中：nx、nz分别为ES和TS单元数；为t时段第x单元ES充、放电功率，为决策变量；为t时段第z单元TS储、放热功率，为决策变量；为ES和TS的成本系数。DR成本表示为当VPP中断用户负荷时，需支付一定的补偿。考虑到不同中断程度对用户的影响程度不同，将中断补偿价格与负荷中断水平挂钩，中断水平越高，补偿价格越高，具体表示如下：Ctdr=Σm=1nm(λmcurtPm,telcurt)]]>式中：nm为中断水平级数；为第m级中断水平补偿价格；为t时段第m级中断水平中断负荷，为决策变量。VPP在运行时需满足约束条件如下：1)DG约束。Pi,tdg≥Piminμi,to]]>Pi,tdg+Ri,tdg≤Pimaxμi,to]]>Ri,tdg≤riutr]]>-rid≤Pi,tdg-Pi,t-1dg≤riu]]>μi,to-μi,t-1o≤μi,tsu]]>μi,t-1o-μi,to≤μi,tsd]]>式中：分别为第i单元DG最大、最小输出功率；为t时段第i单元DG备用容量，为决策变量；riu、rid分别为第i单元DG向上、向下爬坡率；tr为备用服务时间。2)CHP机组约束。Pl,ttchp=klchpPl,techp]]>Pl,techp≥Plminμl,to]]>Pl,techp+Rl,techp≤Plmaxμl,to]]>Rl,techp≤rlutr]]>-rld≤Pl,techp-Pl,t-1echp≤rlu]]>μl,to-μl,t-1o≤μl,tsu]]>μl,t-1o-μl,to≤μl,tsd]]>式中：为t时段第l单元CHP机组供热功率；为第l单元CHP机组热电比，与CHP机组特性有关；分别为第l单元CHP机组最大、最小供电功率；为t时段第l单元CHP机组备用容量，为决策变量；rlu、rld分别为第l单元CHP机组向上、向下爬坡率；布尔变量表示t时段第l单元CHP机组是否运行，是则置1，否则置0。3)锅炉约束。0≤Pk,tboil≤Pkmax]]>式中：为第k单元锅炉最大供热功率。4)ES和TS约束。0≤Px,tesc≤Pxcmax]]>0≤Px,tesd≤Pxdmax]]>Sxmin≤Sx,tes≤Sxmax]]>Sx,tes=Sx,t-1es+ηxescPx,tesc-Px,tesdηxesd]]>Sx,0es=Sxesi]]>Sx,24es=Sxesf]]>0≤Pz,ttsc≤Pzcmax]]>0≤Pz,ttsd≤Pzdmax]]>Szmin≤Sz,tts≤Szmax]]>Sz,tts=Sz,t-1ts+ηztscPz,ttsc-Pz,ttsdηztsd]]>Sz,0ts=Sztsi]]>Sz,24ts=Sztsf]]>式中：分别为第x单元ES最大充、放电功率；为t时段第x单元ES储电量；分别为第x单元ES储电量上、下限；分别为第x单元ES充、放电效率；分别为第x单元ES始、末储电量；分别为第z单元TS最大储、放热功率；为t时段第z单元TS储热量；分别为第z单元TS储热量上、下限；分别为第z单元TS储、放热效率；分别为第z单元TS始、末储热量。5)DR约束。0≤Pm,telcurt≤kmcurtPtel]]>Ptelcurt=Σm=1nmPm,telcurt]]>Ptelcurt+Rtel≤Σm=1nm(kmcurtPtel)]]>式中：为第m级中断水平中断系数；Ptel为t时段电负荷；Ptelcurt为t时段中断负荷；为t时段负荷备用容量，为决策变量。6)电、热功率平衡约束。Σw=1nwPw,twp+Σs=1nsPs,tpv+Σi=1niPi,tdg+Σl=1nlPl,techp+Σx=1nxPx,tesd=Ptem+Ptel-Ptelcurt+Σx=1nxPx,tesc]]>Σl=1nlPl,ttchp+Σk=1nkPk,tboil+Σz=1nzPz,ttsd≥Pttl+Σz=1nzPz,ttsc]]>式中：nw、ns分别为风电机组、光伏机组数；分别为t时段风电机组w、光伏机组s出力；Pttl为t时段热负荷。7)竞标备用容量约束。Rtsrm=ΣiniRi,tdg+ΣlnlRl,techp+Rtel]]>8)VPP系统备用约束。VPP中DG、CHP机组、可中断负荷都可提供系统备用，但不包括已向SRM竞标的备用容量：Σi=1ni(Pimax-Pi,tdg-Ri,tdg)+Σl=1nl(Plmax-Pl,techp-Rl,techp)+(Σm=1nm(kmcurtPtel)-Ptelcurt-Rtel)≥Rta]]>式中：为t时段VPP所需备用容量。进一步，步骤2包括以下步骤：上述模型中EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷均存在不确定性，本文采用RO处理该类不确定性问题，以aij表示上述不确定参数，考虑aij形式如下：aij∈[a~ij-a^ij,a~ij+a^ij]]]>其中：a~ij=12(a‾ij+a‾ij)]]>a^ij=12(a‾ij-a‾ij)]]>式中：aij分别为不确定参数的上、下限，即认为不确定参数在其上、下限区间范围内波动。上述不确定参数形式考虑了不确定参数最坏的情况，由此所做的决策具有很强的保守性，但有失经济性。为此引入鲁棒系数Г，Γ∈[0,|J|]，其中，J为所有不确定参数的集合，此时，不确定参数aij的区间为当Γ＝0时，不考虑不确定参数的不确定性，该模型与确定性优化模型一致，系统鲁棒性较差。随着Γ的不断增大，系统鲁棒性逐渐提高，经济性不断下降。当Γ＝|J|时，即为最保守形式。通过调节鲁棒系数Г，即可得到不同保守程度的最优解，兼顾决策方案的鲁棒性和经济性。采用RO处理EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷的不确定性，所得目标函数及约束条件如下：maxΣt=1T(12(λ‾tem+λ‾tem)Ptem+12(λ‾tsrm+λ‾tsrm)Rtsrm-Ctdg-Ctchp-Ctboil-Cts-Ctdr)-Γmυm-Σt=1T(qtem+qtsrm)]]>υm+qtem≥12(λ‾tem-λ‾tem)ytem]]>υm+qtsrm≥12(λ‾tsrm-λ‾tsrm)ytsrm]]>-ytem≤Ptem≤ytem]]>-ytsrm≤Ptsrm≤ytsrm]]>Pw,twp+Γw,twpυw,twp+qw,twp≤12(P‾w,twp-P‾w,twp)]]>Ps,tpv+Γs,tpvυs,tpv+qs,tpv≤12(P‾s,tpv-P‾s,tpv)]]>Ptel-Γtelυtel-qtel≥12(P‾tel-P‾tel)]]>Pttl-Γttlυttl-qttl≥12(P‾ttl+P‾ttl)]]>υw,twp+qw,twp≥12(P‾w,twp-P‾w,twp)yw,twp]]>υs,tpv+qs,tpv≥12(P‾s,tpv-P‾s,tpv)ys,tpv]]>υtel+qtel≥12(P‾tel-P‾tel)ytel]]>υttl+qttl≥12(P‾ttl-P‾ttl)yttl]]>yw,twp,ys,tpv,ytel,ytel≥1]]>υm,qtem,ytem,qtsrm,ytsrm,υw,twp,qw,twp,yw,twp,]]>υs,tpv,qs,tpv,ys,tpv,υtel,qtel,ytel,υttl,qttl,yttl≥0]]>式中：Ptel、Pbtl分别为EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷上、下限；Γm、分别为电价、风电出力、光伏出力、电负荷和热负荷鲁棒系数，υm、为引入的辅助变量。进一步，步骤3包括以下步骤：当鲁棒系数Γ＜|J|时，不确定参数区间无法囊括所有不确定参数波动情况，难免会给系统带来一定的风险，鲁棒系数越小，风险越大。因此，建立合理的指标量化风险水平，才能更好地平衡VPP系统的鲁棒性与经济性。系统风险的度量指标一般与失负荷量、失负荷持续时间等挂钩，本文主要考虑失负荷量，其对应的风险成本表达式如下：Ctens=λtensPtens]]>式中：为t时段失负荷罚金，当VPP无法供给系统内负荷，需强制切除用户负荷时，要为此支付巨额罚金，因此的数值往往很大。为t时段失负荷量，当VPP内供应电量大于需求电量时，相反，若VPP供电量不足以满足负荷和电力市场需求，则Ptens=Ptel-Ptelcurt+Ptem+Σx=1nxPx,tesc-Σw=1nwPw,twp-Σs=1nsPs,tpv-Σi=1niPi,tdg-Σl=1nlPl,techp-Σx=1nxPx,tesd]]>将风险成本纳入目标函数，即为VPP计及风险后的利润。为计算VPP风险成本，采用蒙特卡罗方法模拟EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷情况。由于每次蒙特卡罗模拟产生的场景不同，所对应失负荷量也并不相同，选取任一场景所得失负荷量来表征系统失负荷量都不尽合理。因此，本文采用期望值表示t时段VPP失负荷量，所得表达式如下：E(Ptens)=Σd=1nd(1ndPd,tens)]]>式中：nd为场景数；为t时段d场景失负荷量。有益效果：本发明具有如下优点和技术效果：(1)本发明提供了一种虚拟电厂热电联合调度优化模型，解决了聚合热电联产机组的虚拟电厂在同时参与能量和旋转备用市场的情况下建模问题；(2)采用鲁棒优化处理能量市场电价、旋转备用市场电价、风电出力、光伏出力、电负荷和热负荷的不确定性，有效降低虚拟电厂面临的风险，并增加虚拟电厂的利润。(3)建立风险量化指标，平衡RO模型的鲁棒性和经济性，从而为决策者提供有效参考。附图说明图1为EM电价示意图；图2为SRM电价示意图；图3为风电出力示意图；图4为光伏出力示意图；图5为电负荷数据示意图；图6为热负荷数据示意图；图7为鲁棒系数对VPP利润和风险成本的影响示意图。具体实施方式下面结合附图和具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。一种虚拟电厂热电联合调度鲁棒优化模型，包括以下步骤：步骤1：建立EM和SRM下VPP日前热电联合调度优化模型；步骤2：采用RO处理EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷的不确定性，建立RO模型；步骤3：建立风险量化指标，衡量系统面临的风险。进一步，步骤1包括以下步骤：对于VPP运营者而言，其目标为净利润最大化，因此优化模型的目标函数如下：maxΣt=1T(Ctm-Ctdg-Ctchp-Ctboil-Cts-Ctdr)]]>目标函数包含六个部分，分别为VPP参与电力市场所获利润DG成本CHP机组成本锅炉成本储能成本DR成本每部分具体表达式如下：Ctm=λtemPtem+λtsrmRtsrm]]>式中：分别为t时段EM电价和SRM电价；分别为t时段VPP在EM和SRM的竞标量，为决策变量。DG成本包括运行成本、启停成本和环境成本：Ctdg=Σi=1ni(kiPi,tdg+kifμi,to)+(λisuμi,tsu+λisdμi,tsd)+Pi,tdgΣe=1neQi,tdg(Ve+Ye)]]>式中：ni为DG单元数；为t时段第i单元DG输出功率，为决策变量；ki、为第i单元DG的燃料成本、固定成本、启动成本和停止成本；布尔变量分别表示t时段第i单元DG是否工作、启动、停止，是则置1，否则置0；ne为考虑的污染物总数；为第i单元DG第e项污染物排放量；Ve、Ye分别为第e项污染物环境价值、罚款数量级。CHP机组成本包括燃料成本、启停成本和环境成本，锅炉成本包括燃料成本和环境成本，本文考虑的CHP机组和锅炉均以天然气为燃料，如下式：Ctchp=Σl=1nl860λtngPl,techpHngηlchp+(λlsuμl,tsu+λlsdμl,tsd)+Pl,techpηlchpΣe=1neQl,echp(Ve+Ye)]]>Ctboil=Σk=1nk(860λtngPk,tboilHngηkboil+Pk,tboilηkboilΣe=1neQk,eboil(Ve+Ye))]]>式中：nl、nk分别为CHP机组和锅炉单元数；为t时段天然气价格；Hng为天然气热值；860为kWh转化为kcal的单位转换比率；为t时段第l单元CHP机组供电功率和第k单元锅炉供热功率，为决策变量；为第l单元CHP机组和第k单元锅炉效率，需要说明的是，仅为CHP机组的供电效率，并非整体效率；为第l单元CHP启动和停止成本；布尔变量分别表示t时段第l单元CHP是否启动、停止，是则置1，否则置0；为第l单元CHP机组和第k单元锅炉第e项污染物排放量，Ve、Ye分别为第e项污染物环境价值、罚款数量级；储能成本包括ES成本和TS成本，其与充、放电功率和储、放热功率近似呈线性关系：Cts=Σx=1nx(axes(Px,tesc+Px,tesd)+bxes)+Σz=1nz(azts(Pz,ttsc+Pz,ttsd)+bzts)]]>式中：nx、nz分别为ES和TS单元数；为t时段第x单元ES充、放电功率，为决策变量；为t时段第z单元TS储、放热功率，为决策变量；为ES和TS的成本系数。DR成本表示为当VPP中断用户负荷时，需支付一定的补偿。考虑到不同中断程度对用户的影响程度不同，将中断补偿价格与负荷中断水平挂钩，中断水平越高，补偿价格越高，具体表示如下：Ctdr=Σm=1nm(λmcurtPm,telcurt)]]>式中：nm为中断水平级数；为第m级中断水平补偿价格；为t时段第m级中断水平中断负荷，为决策变量。VPP在运行时需满足约束条件如下：1)DG约束。Pi,tdg≥Piminμi,to]]>Pi,tdg+Ri,tdg≤Pimaxμi,to]]>Ri,tdg≤riutr]]>-rid≤Pi,tdg-Pi,t-1dg≤riu]]>μi,to-μi,t-1o≤μi,tsu]]>μi,t-1o-μi,to≤μi,tsd]]>式中：分别为第i单元DG最大、最小输出功率；为t时段第i单元DG备用容量，为决策变量；riu、rid分别为第i单元DG向上、向下爬坡率；tr为备用服务时间。2)CHP机组约束。Pl,ttchp=klchpPl,techp]]>Pl,techp≥Plminμl,to]]>Pl,techp+Rl,techp≤Plmaxμl,to]]>Rl,techp≤rlutr]]>-rld≤Pl,techp-Pl,t-1echp≤rlu]]>μl,to-μl,t-1o≤μl,tsu]]>μl,t-1o-μl,to≤μl,tsd]]>式中：为t时段第l单元CHP机组供热功率；为第l单元CHP机组热电比，与CHP机组特性有关；Plmax、Plmin分别为第l单元CHP机组最大、最小供电功率；为t时段第l单元CHP机组备用容量，为决策变量；分别为第l单元CHP机组向上、向下爬坡率；布尔变量表示t时段第l单元CHP机组是否运行，是则置1，否则置0。3)锅炉约束。0≤Pk,tboil≤Pkmax]]>式中：为第k单元锅炉最大供热功率。4)ES和TS约束。0≤Px,tesc≤Pxcmax]]>0≤Px,tesd≤Pxdmax]]>Sxmin≤Sx,tes≤Sxmax]]>Sx,tes=Sx,t-1es+ηxescPx,tesc-Px,tesdηxesd]]>Sx,0es=Sxesi]]>Sx,24es=Sxesf]]>0≤Pz,ttsc≤Pzcmax]]>0≤Pz,ttsd≤Pzdmax]]>Szmin≤Sz,tts≤Szmax]]>Sz,tts=Sz,t-1ts+ηztscPz,ttsc-Pz,ttsdηztsd]]>Sz,0ts=Sztsi]]>Sz,24ts=Sztsf]]>式中：分别为第x单元ES最大充、放电功率；为t时段第x单元ES储电量；分别为第x单元ES储电量上、下限；分别为第x单元ES充、放电效率；分别为第x单元ES始、末储电量；分别为第z单元TS最大储、放热功率；为t时段第z单元TS储热量；分别为第z单元TS储热量上、下限；分别为第z单元TS储、放热效率；分别为第z单元TS始、末储热量。5)DR约束。0≤Pm,telcurt≤kmcurtPtel]]>Ptelcurt=Σm=1nmPm,telcurt]]>Ptelcurt+Rtel≤Σm=1nm(kmcurtPtel)]]>式中：为第m级中断水平中断系数；Ptel为t时段电负荷；Ptelcurt为t时段中断负荷；为t时段负荷备用容量，为决策变量。6)电、热功率平衡约束。Σw=1nwPw,twp+Σs=1nsPs,tpv+Σi=1niPi,tdg+Σl=1nlPl,techp+Σx=1nxPx,tesd=Ptem+Ptel-Ptelcurt+Σx=1nxPx,tesc]]>Σl=1nlPl,ttchp+Σk=1nkPk,tboil+Σz=1nzPz,ttsd≥Pttl+Σz=1nzPz,ttsc]]>式中：nw、ns分别为风电机组、光伏机组数；分别为t时段风电机组w、光伏机组s出力；Pttl为t时段热负荷。7)竞标备用容量约束。Rtsrm=ΣiniRi,tdg+ΣlnlRl,techp+Rtel]]>8)VPP系统备用约束。VPP中DG、CHP机组、可中断负荷都可提供系统备用，但不包括已向SRM竞标的备用容量：Σi=1ni(Pimax-Pi,tdg-Ri,tdg)+Σl=1nl(Plmax-Pl,techp-Rl,techp)+(Σm=1nm(kmcurtPtel)-Ptelcurt-Rtel)≥Rta]]>式中：为t时段VPP所需备用容量。进一步，步骤2包括以下步骤：上述模型中EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷均存在不确定性，本文采用RO处理该类不确定性问题，以aij表示上述不确定参数，考虑aij形式如下：aij∈[a~ij-a^ij,a~ij+a^ij]]]>其中：a~ij=12(a‾ij+a‾ij)]]>a^ij=12(a‾ij-a‾ij)]]>式中：aij分别为不确定参数的上、下限，即认为不确定参数在其上、下限区间范围内波动。上述不确定参数形式考虑了不确定参数最坏的情况，由此所做的决策具有很强的保守性，但有失经济性。为此引入鲁棒系数Г，Γ∈[0,|J|]，其中，J为所有不确定参数的集合，此时，不确定参数aij的区间为当Γ＝0时，不考虑不确定参数的不确定性，该模型与确定性优化模型一致，系统鲁棒性较差。随着Γ的不断增大，系统鲁棒性逐渐提高，经济性不断下降。当Γ＝|J|时，即为最保守形式。通过调节鲁棒系数Г，即可得到不同保守程度的最优解，兼顾决策方案的鲁棒性和经济性。采用RO处理EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷的不确定性，所得目标函数及约束条件如下：maxΣt=1T(12(λ‾tem+λ‾tem)Ptem+12(λ‾tsrm+λ‾tsrm)Rtsrm-Ctdg-Ctchp-Ctboil-Cts-Ctdr)-Γmυm-Σt=1T(qtem+qtsrm)]]>υm+qtem≥12(λ‾tem-λ‾tem)ytem]]>υm+qtsrm≥12(λ‾tsrm-λ‾tsrm)ytsrm]]>-ytem≤Ptem≤ytem]]>-ytsrm≤Ptsrm≤ytsrm]]>Pw,twp+Γw,twpυw,twp+qw,twp≤12(P‾w,twp+P‾w,twp)]]>Ps,tpv+Γs,tpvυs,tpv+qs,tpv≤12(P‾s,tpv+P‾s,tpv)]]>Ptel-Γtelυtel-qtel≥12(P‾tel+P‾tel)]]>Pttl-Γttlυttl-qttl≥12(P‾ttl+P‾ttl)]]>υw,twp+qw,twp≥12(P‾w,twp-P‾w,twp)yw,twp]]>υs,tpv+qs,tpv≥12(P‾s,tpv-P‾s,tpv)ys,tpv]]>υtel+qtel≥12(P‾tel-P‾tel)ytel]]>υttl+qttl≥12(P‾ttl-P‾ttl)yttl]]>yw,twp,ys,tpv,ytel,yttl≥1]]>υm,qtem,ytem,qtsrm,ytsrm,υw,twp,qw,twp,yw,twp,]]>υs,tpv,qs,tpv,ys,tpv,υtel,qtel,ytel,υttl,qttl,yttl≥0]]>式中：Ptel、Pttl分别为EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷上、下限；Γm、分别为电价、风电出力、光伏出力、电负荷和热负荷鲁棒系数，υm、为引入的辅助变量。进一步，步骤3包括以下步骤：当鲁棒系数Γ＜|J|时，不确定参数区间无法囊括所有不确定参数波动情况，难免会给系统带来一定的风险，鲁棒系数越小，风险越大。因此，建立合理的指标量化风险水平，才能更好地平衡VPP系统的鲁棒性与经济性。系统风险的度量指标一般与失负荷量、失负荷持续时间等挂钩，本文主要考虑失负荷量，其对应的风险成本表达式如下：Ctens=λtensPtens]]>式中：为t时段失负荷罚金，当VPP无法供给系统内负荷，需强制切除用户负荷时，要为此支付巨额罚金，因此的数值往往很大。为t时段失负荷量，当VPP内供应电量大于需求电量时，相反，若VPP供电量不足以满足负荷和电力市场需求，则Ptens=Ptel-Ptelcurt+Ptem+Σx=1nxPx,tesc-Σw=1nwPw,twp-Σs=1nsPs,tpv-Σi=1niPi,tdg-Σl=1nlPl,techp-Σx=1nxPx,tesd]]>将风险成本纳入目标函数，即为VPP计及风险后的利润。为计算VPP风险成本，采用蒙特卡罗方法模拟EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷情况。由于每次蒙特卡罗模拟产生的场景不同，所对应失负荷量也并不相同，选取任一场景所得失负荷量来表征系统失负荷量都不尽合理。因此，本文采用期望值表示t时段VPP失负荷量，所得表达式如下：E(Ptens)=Σd=1nd(1ndPd,tens)]]>式中：nd为场景数；为t时段d场景失负荷量。下面以一VPP为例介绍本发明：本VPP包括4个DG(包括2个微型燃气轮机、2个燃料电池)、3个风电机组、2个光伏机组、5个CHP机组、1个锅炉、5个ES单元、5个TS单元、区域内电负荷和热负荷。VPP调度周期为1天，分为24时段。EM电价、SRM电价、风电出力、光伏出力、电负荷和热负荷上、下限如图1-6所示。SRM备用服务时间为10min，失负荷罚金为1000$/MW。1)VPP行为对利润影响为衡量VPP参与EM和SRM、聚合CHP机组以及VPP内CHP机组参与SRM行为对利润的影响，以确定性优化模型为例，构建以下5种不同方案，方案设置和所得结果如表1所示。表15种不同的VPP构建方案从表1方案1、2、5对比可以看出，VPP只参与EM或SRM时利润均小于同时参与EM和SRM情景，其中，只参与SRM时利润更低。就方案3而言，需要说明的是，为比较热电联供和热电分供对VPP利润的影响，分别用与CHP机组最大输出功率相同的DG和锅炉替代CHP机组的供电和供热输出，结果表明，以VPP形式聚合CHP机组实现热电联供能增加VPP利润。与方案5相比，方案4未考虑CHP机组参与SRM情景，降低了决策的灵活性，因而利润降低。综上所述，VPP参与EM和SRM、聚合CHP机组、VPP内CHP机组参与SRM行为均能有效增加VPP利润。VPP中不确定性的本质是其包含的各类不确定性的汇总，其中包含不确定性的叠加或抵消，采用RO处理单类不确定性所得结果往往不尽合理。因此，本文考虑在采用RO处理上述所有不确定性的情况下，不计风险时VPP利润、计及风险后VPP利润和风险成本随鲁棒系数的变化情况，所得结果如图7所示。可以看出：不计风险时VPP利润和风险成本随鲁棒系数的增大逐渐降低，而计及风险后VPP利润随鲁棒系数的增大呈现先上升后下降的趋势，并在鲁棒系数为30％时达到最大值。这是由于鲁棒系数的增大提高了决策的保守性，从而降低了经济性，因此不计风险时VPP利润降低。但是，鲁棒系数的增大也提高了系统的鲁棒性，鲁棒系数越大，系统鲁棒性越强，失负荷风险越低，表现为风险成本降低，计及风险后VPP利润有所提高。然而，鲁棒系数过大时，VPP风险成本的降低不足以弥补保守策略带来的损失，计及风险后VPP利润仍会降低。当鲁棒系数达到100％时，不确定参数区间囊括所有不确定参数波动情况，此时系统风险成本为0，但其决策过于保守，因此计及风险后利润最低。此外，图中鲁棒系数为0点即确定性优化模型结果，说明考虑VPP面临风险时，RO模型能提高VPP利润。以上仿真结果验证了本发明所构模型有效性和实用性，说明VPP参与EM和SRM、聚合CHP机组和VPP内CHP机组参与SRM行为均能有效增加VPP利润。并且，RO模型提高了系统的鲁棒性，降低了系统风险，从而增加了VPP利润，而风险成本很好地刻画了VPP面临的风险，降低了不确定性决策的盲目性，从而为决策者选取合适的鲁棒系数提供有效参考。当前第1页1 2 3