一种电力系统同步相量快速计算方法与流程

本发明是关于一种电力系统同步相量快速计算方法，涉及电力系统自动测量
技术领域：
。
背景技术：
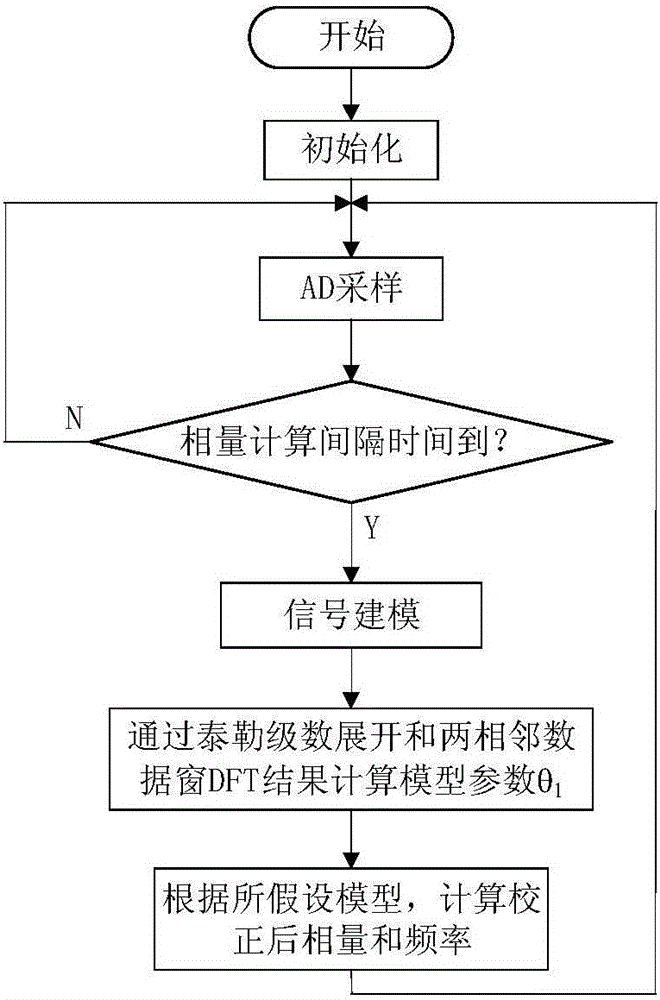
：近年来，以同步相量测量装置(PhasorMeasurementUnit，PMU)为基础的广域测量系统在电力系统动态过程监视、在线辨识、安全稳定分析以及广域控制等领域中得到广泛的应用。随着广域测量系统应用研究的不断深入，PMU对同步相量测量的要求越来越高，其相量算法的准确性将直接影响到相关应用功能的可靠性。传统DFT(DiscreteFourierTransform，离散傅里叶变换)算法，在频率偏移额定频率时，由于频谱泄漏精度难以满足要求。目前已有仅仅通过两个数据窗对DFT计算结果进行修正的相量测量算法，相对于传统的DFT算法，该算法较大地提高了计算精度，但是由于简化过程所做近似较大，在频率偏差较大时同样难以满足精度要求。技术实现要素：针对上述问题，本发明的目的是提供一种能够显著提高相量计算精度的电力系统同步相量快速计算方法。为实现上述目的，本发明采取以下技术方案：一种电力系统同步相量快速计算方法，其特征在于包括以下步骤：1)初始化，确定每周波采样点数N以及两相邻数据窗相隔点数l；2)判断是否达到电力信号相量计算间隔时间，如果是，则进入步骤3)，否，则继续等待；3)对电力信号进行建模；4)对电力信号进行每周波N点采样，得离散化电力信号，对离散化电力信号加数据窗后进行DFT变换，并对DFT变换后的电力信号的相量进行校正；5)对相隔l点的另一数据窗内的电力信号进行DFT计算，结合电力信号模型，通过计算电力模型参数，进而得到校正后电力信号的相量和频率。进一步地，对电力信号进行建模，得到电力信号x(t)的表达式：x(t)=P(t)ej2πf0t+P*(t)e-j2πf0t]]>式中，P(t)表示电力信号的动态相量，P(t)＝a(t)ejθ(t)，a(t)和θ(t)分别表示电力信号幅值和相角的多项式，f0为额定频率，假设计算周期内幅值恒定，频率偏差恒定，即a(t)＝a，θ(t)＝θ0+θ1t，其中，模型参数a、θ0和θ1均为常数。进一步地，4)对电力信号进行每周波N点采样，得离散化电力信号，对离散化电力信号加数据窗后进行DFT变换，并对DFT变换后的电力信号的相量进行校正：X=acejθc=aejθ0·ejθ1(N-1)2Nf0·A·(1+e-jC·B)]]>式中，a和θ0分别表示校正后电力信号的幅值和相角；ac和θc分别表示校正前通过DFT变换得到的电力信号的幅值和相角；其中，A、B、C分别表示：A=1Nsin(θ12f0)/sin(θ12Nf0)B=sin(θ12Nf0)/sin(θ1+4πf02Nf0)C=2θ0+(2πf0+θ1)(N-1)Nf0---(1)]]>通过泰勒级数展开可近似为：A≈24f02-θ1224f02]]>B≈3N2·θ14π(3N2-2π2)·f0+(3N2-6π2)·θ1]]>(1+e-jC·B)≈1+B2+2BcosC·e-jBsinC1+BcosC---(2)]]>基于上述公式，可以得到校正后电力信号相量与校正前DFT变换直接计算相量的关系：a≈ac24f02-θ1224f02·1+B2+2BcosC---(3)]]>θ0≈θc+D-θ1(N-1)2Nf0---(4)]]>式中，D＝BsinC/(1+BcosC)对D进行泰勒展开并舍去高次项后得：D=Bsin(2θc-2πN)1-Bcos(2θc-2πN).]]>进一步地，5)对相隔l点的另一数据窗内的电力信号进行DFT计算，结合电力信号模型，通过计算电力模型参数，进而得到校正后电力信号的相量和频率，具体过程为：首先得到关于B的一元二次方程：E·B2+F·B+G＝0式中：E=12(sin(4θc-4πN)-sin(4θcl-4πN))-L(sin(2θc-2πN)-sin(2θcl-2πN))]]>F=sin(2θc-2πN)-sin(2θcl-2πN)-(θc-θcl)L+2πNlL-2πlNf0H]]>G=θc-θcl-2πNl]]>H=2π(6N2-4π2)3N2]]>L=1-2π2N2]]>式中，θcl表示相隔l点的数据窗内电力信号校正前DFT计算相角；通过上式可求得：进而求得将θ1代入公式(4)求得校正后电力信号的相角θ0；将θ0和θ1代入公式(3)求得校正电力信号幅值a；校正后电力信号频率f＝f0+θ1/(2π)。本发明由于采取以上技术方案，其具有以下优点：1、本发明根据国家标准或者现场实际的特定精度要求进行泰勒级数展开简化，并通过两相邻数据窗DFT结果进行校正，运算量少，且抑制谐波能力强，从而显著提高相量计算精度。2、采用本发明在频率偏差较大时，其稳态精度指标依然满足国标《电力系统同步相量测量装置检测规范》和IEEEC37.118.1标准要求。本发明可以广泛应用于电力系统同步相量快速计算中。附图说明图1是本发明实施例的测量装置结构示意图；图2是本发明电力系统同步相量快速计算方法流程示意图；图3是本发明方法实施例的算法流程示意图。具体实施方式以下结合附图来对本发明进行详细的描绘。然而应当理解，附图的提供仅为了更好地理解本发明，它们不应该理解成对本发明的限制。如图1所示，本发明的电力系统同步相量快速计算方法可以基于各种测量装置进行实现，在此不再赘述。本发明实施例的测量装置包括PMU装置和三相电压电流互感器，PMU装置通过二次电压电流互感器将大电压(额定电压100V)或大电流信号(额定电压5A)转换为小电压信号(电压范围0至5V)，通过AD模块对小电压信号进行模数转换，DSP处理器根据GPS的秒脉冲对模数转换后的小电压数字信号进行时间同步的等间隔采样，其中，本实施例的DSP处理器可以采用浮点DSP处理器，但是不限于此。如图2所示，本发明提供的电力系统同步相量快速计算方法，包括以下内容：1、初始化，确定每周波(每周波可以为20ms，但是不限于此)采样点数N，两相邻数据窗相隔点数l。2、判断是否达到电力信号相量(幅值和相角)计算间隔时间，如果是，则进入步骤3，否，则继续等待。3、对电力信号x(t)进行建模，得到电力信号x(t)的表达式：x(t)=P(t)ej2πf0t+P*(t)e-j2πf0t]]>式中，P(t)表示电力信号的动态相量，P(t)＝a(t)ejθ(t)，a(t)和θ(t)分别表示电力信号幅值和相角的多项式，f0为额定频率。假设计算周期内幅值恒定，频率偏差恒定，即a(t)＝a，θ(t)＝θ0+θ1t，其中，模型参数a、θ0和θ1均为常数。4、对电力信号x(t)进行每周波N点采样，得离散化电力信号，对离散化电力信号加数据窗后进行DFT变换，并对DFT变换后的电力信号的相量进行校正：X=acejθc=aejθ0·ejθ1(N-1)2Nf0·A·(1+e-jC·B)]]>式中，a和θ0分别表示校正后电力信号的幅值和相角；ac和θc分别表示校正前通过DFT变换得到的电力信号的幅值和相角；其中，A、B、C分别表示：A=1Nsin(θ12f0)/sin(θ12Nf0)B=sin(θ12Nf0)/sin(θ1+4πf02Nf0)C=2θ0+(2πf0+θ1)(N-1)Nf0---(1)]]>通过泰勒级数展开可近似为：A≈24f02-θ1224f02]]>B≈3N2·θ14π(3N2-2π2)·f0+(3N2-6π2)·θ1]]>(1+e-jC·B)≈1+B2+2BcosC·e-jBsinC1+BcosC---(2)]]>基于上述公式，可以得到校正后电力信号相量与校正前DFT变换直接计算相量的关系：a≈ac24f02-θ1224f02·1+B2+2BcosC---(3)]]>θ0≈θc+D-θ1(N-1)2Nf0---(4)]]>式中，D＝BsinC/(1+BcosC)对D进行泰勒展开并舍去高次项后得：D=Bsin(2θc-2πN)1-Bcos(2θc-2πN).]]>5、对相隔l点的另一数据窗内的电力信号进行DFT计算，结合电力信号模型，通过计算电力模型参数，进而得到校正后电力信号的相量和频率，具体为：首先得到关于B的一元二次方程：E·B2+F·B+G＝0式中：E=12(sin(4θc-4πN)-sin(4θcl-4πN))-L(sin(2θc-2πN)-sin(2θcl-2πN))]]>F=sin(2θc-2πN)-sin(2θcl-2πN)-(θc-θcl)L+2πNlL-2πlNf0H]]>G=θc-θcl-2πNl]]>H=2π(6N2-4π2)3N2]]>L=1-2π2N2]]>式中，θcl表示相隔l点的数据窗内电力信号校正前DFT计算的相角。通过上式可求得：进而求得将θ1代入公式(4)求得校正后电力信号的相角θ0；将θ0和θ1代入公式(3)的计算公式，求得校正后电力信号幅值a，校正后电力信号频率f＝f0+θ1/(2π)。为了进一步验证本发明的电力系统同步相量快速计算方法的正确性，下面通过具体实施例对本发明方法进行仿真测试，仿真过程中采样频率为6400Hz等间隔采样，两相邻数据窗的间隔取为64点。1、频率偏差测试电力系统在不同运行模式下，实际频率将偏移额定频率。特别是在发生故障时，将会导致较大的频率偏差。为了测试相量测量方法在实际频率偏离额定频率时的性能，国标《电力系统同步相量测量装置检测规范》规定频率测量范围是45Hz～55Hz，在基波频率偏离额定值5Hz时，电压、电流幅值测量误差改变量应小于额定频率时测量误差极限值的100％，相角测量误差改变量应不大于1°。表1为本发明在频率偏离额定频率5Hz时的测试结果。从表1中可以看出，本发明的量测精度远高于标准要求。表1频率偏差为5Hz时相量测试结果最大误差平均绝对误差均方根误差角度误差-0.0022°0.0009°0.0012°幅值误差0.0072％0.0071％0.0071％2、频率斜坡响应测试频率变化率是系统解列的重要依据，也是系统切机和切负荷时的重要参数。IEEEC37.118.1中在频率斜坡测试中对测量级PMU的规定是：最大的综合矢量误差为1％，最大频率误差为0.01Hz，最大频率变化率误差为0.2Hz/s。本发明方法在频率偏差5Hz，频率变化率1Hz/s的斜坡测试信号下，误差统计结果如表2所示，可以看出各项指标均满足IEEE标准。表2频率斜坡响应测试结果最大误差平均绝对误差均方根误差角度误差(°)0.05370.04460.0449幅值误差(％)-0.0120％0.0069％0.0077％频率误差(Hz)0.001050.001020.00102频率变化率误差(Hz/s)0.008810.008710.00870上述各实施例仅用于说明本发明，其中方法的各实施步骤等都是可以有所变化的，凡是在本发明技术方案的基础上进行的等同变换和改进，均不应排除在本发明的保护范围之外。当前第1页1 2 3