基于自适应耦合观测与非线性压缩学习的光谱成像方法与流程
本发明属于图像处理技术领域,特别涉及一种压缩光谱成像方法,可用于高光谱图像的低成本与高质量获取。
背景技术:
压缩感知是近年来信号处理技术领域中发展起来的一种新的采样理论,利用信号的稀疏特性,可在远小于传统奈奎斯特采样率的条件下,实现信息的精确恢复。目前现存的压缩感知的方法均是基于显式的线性稀疏表示模型的。线性稀疏表示模型具有简单直观,容易理解,容易操作等优势。但是,实际场景信息比较复杂,很难在线性稀疏表示模型下获得足够稀疏的表示。如果使用线性稀疏表示模型,则获得稀疏系数的稀疏度较低,这就使得恢复出原信号所需要的测量值更多。另一方面,对于压缩感知技术在压缩成像中的应用,设计一个较好的观测系统能够提高成像质量。目前现有压缩成像方法大都是基于随机观测,观测矩阵被选为高斯随机矩阵,或者贝努利随机矩阵。然而,这类随机观测矩阵能够与大多数的正交字典不相关,满足有限等距特性条件,但该随机观测矩阵仍属于非自适应观测矩阵,其虽具有普适性,但对于不同的信号,由于没有充分挖掘信号的信息,且不具备自适应性和最优性,无法在少量传感器下获得高质量的压缩成像结果。
技术实现要素:
本发明的目的在于针对上述已有技术的不足,提出了一种基于自适应耦合观测与非线性压缩学习的光谱成像方法,以使观测矩阵与学习到的字典具有更好的非相关性,在少量观测下提高压缩成像的质量。
本发明的技术方案是,通过非线性核函数,把原始空间中的信号投影到特征空间上,并在特征空间中进行字典学习;通过类似K-SVD的方法,对由稀疏字典和初始观测矩阵的乘积所组成的感知矩阵进行迭代训练,得到一个经过耦合优化的观测矩阵;通过核压缩感知的方法实现非线性压缩感知光谱成像。其实现步骤包括如下:
(1)选取三组n1×n2×n3的高光谱图像,除第10谱段外随机选择n个谱段构造训练样本矩阵Y=[y1,y2,…,yj,…,yn],其中,n1×n2为高光谱图像的大小,n3表示总谱带的数目,yj表示第j个谱段拉成的列向量,j=1,2,…,n,n为训练样本的个数;
(2)利用训练样本矩阵Y训练字典,采用核主成份分析KPCA的方法求出训练样本的稀疏字典,记为n为样本个数,K为得到的稀疏字典的原子个数;
(3)设测量值的点数为m,并随机生成高斯随机矩阵作为初始观测矩阵i=1,2,…,m,φi是初始化观测矩阵Φ0的行向量;
(4)根据稀疏字典A,结合训练样本矩阵Y和初始观测矩阵Φ0,得到感知矩阵G=f(Φ0T)Tf(Y)A,对感知矩阵G进行训练,得到最终观测矩阵Φ,其中f为非线性映射函数,T表示转置;
(5)将三组第10谱段图像拉成列向量作为测试样本,分别记为e1,e2,e3;
(6)根据上述(4)所求的观测矩阵Φ,对(5)中的三幅测试样本e1,e2,e3进行非线性压缩成像,得到测量值m=fk(<Φ,ei>),其中ei表示第i组测试样本,i从1到3,fk为选择的核函数;
(7)利用最小二乘法计算稀疏系数其中表示伪逆;
(8)根据稀疏系数β以及稀疏字典A,利用pre-image方法重构出原图像其中为第i组恢复的图像。
本发明与现有的技术相比有以下优点:
1.本发明提出的核空间中的自适应耦合优化算法,使得观测矩阵与经过字典学习得到的稀疏字典具有更高的非相关性,能够更好的满足压缩感知理论的限制等距特性条件。
2.本发明根据字典学习所得到的稀疏字典来进行耦合优化得出观测矩阵,可以充分挖掘信号的信息,更具有自适应性,从而获得更好的重构效果。
附图说明
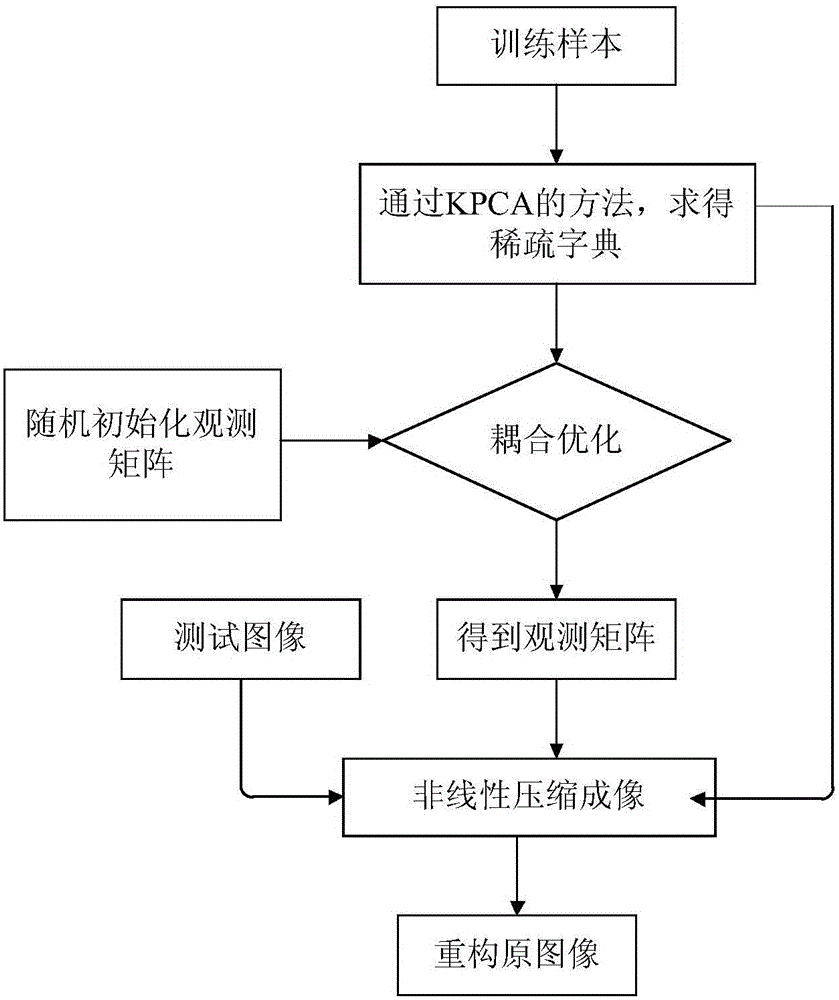
图1是本发明的实现流程图;
图2是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像IndianPines的重构效果对比图;
图3是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像IndianPines进行重构所恢复图像的均方误差曲线图;
图4是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像Moffet的重构效果对比图;
图5是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像Moffet进行重构所恢复图像的均方误差曲线图;
图6是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像WashtonDC的重构效果对比图;
图7是用本发明方法和以高斯随机矩阵作为观测矩阵的方法在采样率为10%时对测试图像WashtonDC进行重构所恢复图像的均方误差曲线图。
具体实施方法
参照图1,本发明的具体实现步骤如下:
步骤1.构建训练样本矩阵。
从图像库获取三组n1×n2×n3的高光谱图像,将每组高光谱图像的第10谱段的图像作为测试样本,其它的n个谱段作为训练样本,并把训练样本的每个谱段图像拉成列向量,组成大小为w×n的训练样本矩阵:Y=[y1,y2,…,yj,…,yn],其中,w=n1×n2yj表示每个谱段拉成的列向量,j=1,2,…,n。
步骤2.利用训练样本Y训练字典。
在非线性压缩成像中,训练字典的方法有核主成份分析、核K-SVD和核独立成分分析等方法,核主成份分析方法训练字典的时间相对较短,因此本发明采用核主成份分析KPCA的方法对训练样本进行训练,求出稀疏字典,其步骤如下:。
2a)选定核函数为多项式核函数k(x,y)=fk(<x,y>)=(<x,y>+c)d,其中x,y为核函数的输入变量,c为核函数的截距参数,其值为c=0.5,d为指数参数,其值为d=5;
2b)利用2a)选定的核函数求样本矩阵Y的核矩阵:
C=k(Y,Y)=(<Y,Y>+c)d
其中n为样本个数;
2c)对核矩阵C进行特征值分解,即C=VΣVT,其中Σ是对角矩阵,V是特征值所对应的特征向量矩阵,T表示转置;
2d)设贡献度Z=0.9,计算对角矩阵Σ中每一个正的特征值在所有正的特征值总和中的贡献率,根据降序排列的特征值的顺序,依次累加正的特征值的贡献率,当累加后的总和大于贡献率Z时停止,把所累加的特征值的数量记为p;
2e)根据前p个最大的特征值的特征向量,得出相对应的特征向量矩阵Vp,则稀疏字典A=Vp。
步骤3.生成初始观测矩阵Φ0。
设测量值的点数为m,随机生成大小为m×w的高斯随机矩阵,作为初始观测矩阵:φi是初始化观测矩阵Φ0的第i个行向量,i=1,2,…,m。
步骤4.根据稀疏字典A,结合训练样本矩阵Y和初始观测矩阵Φ0,得到感知矩阵G。
将稀疏字典A、训练样本矩阵Y、初始观测矩阵Φ0三者相乘,得到感知矩阵:G=f(Φ0T)Tf(Y)A,其中f表示非线性映射函数,T表示转置。
步骤5.对感知矩阵G进行训练,得到最终观测矩阵Φ。
5a)选定核函数为多项式核函数k(x,y)=fk(<x,y>)=(<x,y>+c)d,c为核函数的截距参数,其值为c=0.5,d为指数参数,其值为d=5;
5b)计算感知矩阵G的格兰姆矩阵GTG,求解下列优化问题得到与特征空间中稀疏字典相关性最小的观测矩阵:
其中IK是大小为K×K的单位矩阵,F表示矩阵的Frobenius范数;
5c)将上述优化问题转化为GTG≈IK,把感知矩阵G=f(Φ0T)Tf(Y)A代入GTG≈IK,并对其两边分别左乘稀疏字典A,右乘其转置AT,得到如下关系式:
AATf(Y)Tf(Φ0T)f(Φ0T)Tf(Y)AAT≈AAT;
5d)对上述AAT进行奇异值分解,即AAT=VΛVT,其中,是奇异值分解后所求得的正交矩阵,是对角矩阵,n为训练样本的数量;
5e)将AAT=VΛVT代入5c)中的公式,得到如下关系式:
VΛVTf(Y)Tf(Φ0T)f(Φ0T)Tf(Y)VΛVT≈VΛVT
5f)根据样本矩阵Y以及初始化观测矩阵Φ0,结合核函数,计算过渡核矩阵Knm:
5g)把5e)的公式化简为:
其中,中间变量
5h)把对角矩阵Λ写成diag(λ1,…,λn),将中间变量Γmn写成行向量形式Γmn=[τ1,…,τm]T,并把目标函数转化为其中,vi=[λ1τi,1,…,λnτi,n];
5i)将展开为:
同时,定义误差矩阵为:
5j)根据过渡核矩阵Knm以及正交矩阵V,利用下式初始化Γmn:
5k)设置循环次数t的最大值为m,t从1开始循环;
5l)在第t次循环中,计算误差矩阵Et,并对其进行特征值分解,得到最大的特征值ξt以及与其对应的特征向量ut;
5m)根据下式,更新的每一个行向量:
5n)循环m次,就能得到具有最小相关性的中间变量
5o)计算过渡核矩阵
5p)求解下式得到经过耦合优化的观测矩阵Φ:
其中,k(x,y)=fk(<x,y>)。
步骤6.获取测试图像。
把三组高光谱图像的第10个谱段的图像作为测试图像,并把其拉成列向量,分别记为e1,e2,e3。
步骤7.根据上述步骤2所求的字典A和步骤4所求的观测矩阵Φ,利用核压缩感知的方法对步骤5中的三幅测试图像e1,e2,e3进行非线性压缩成像。
7a)根据压缩观测方程M=Gβ的形式,计算测量值向量M和感知矩阵G:
7b)根据计算得到的测量值向量M和感知矩阵G,采用最小二乘算法得出稀疏系数
步骤8.根据稀疏系数β以及稀疏字典A,重构出原图像
利用pre-image方法,通过如下公式重构出原图像i=1,2,3:
其中,up表示单位正交基的第p列,p=1,2,…,w,w是高光谱图像的像素点的个数,Aβ=[c1,c2,…,cj,…,cn]T,cj表示Aβ的第j个元素,fk为先前选定的多项式核函数,是fk的逆函数。
本发明的效果可以通过以下实验进一步说明:
1)实验条件
本实验所用的三组高光谱图像为典型的AVIRIS高光谱数据:IndianPines、Moffet和WashtonDC。IndianPines数据是1992年由AVIRIS传感器对印第安那州西北农业区成像所得,Moffet图像是由1992年8月由AVIRIS传感器对加利福尼亚州的Moffett地区成像所得;两组图像波长范围为0.4um~2.5um,共224个光谱段,去掉所有像素为0和不透明的波段后有200个谱段,空间分辨率为20m。WashtonDC图像由HYDICE光谱仪对Washtington DC Mall地区成像而来,波长范围为0.4um~2.5um,共210个谱段,预处理后选191个波段,空间分辨率为2.8m。IndianPines图像的大小为145×145×200,Moffet图像的大小为145×145×200,WashtonDC图像的大小为145×145×191。
实验仿真环境:采用软件MATLAB 2012R作为仿真工具,CPU是AMD A8-5550M,主频为2.10GHz,内存16G,操作系统为Windows 7旗舰版。
从每组高光谱图像中随机抽取第10个谱段作为测试图像,取每组高光谱图像其他谱段的图像作为训练样本。
2)仿真内容
仿真1:在0.1%~20%的不同采样率下,分别采用本发明方法与现有以高斯随机矩阵作为观测矩阵的方法对测试图像进行非线性压缩感知仿真实验,实验结果如表1所示。
表1 不同采样率下两种方法的实验对比
从表1可以看出,随着采样率的不断提高,两种方法的PSNR不断上升,说明重构效果都在稳步提升,但是本发明方法提升幅度最大。在相同的采样率下,本发明方法的PSNR最高,重构效果最好。
仿真2:在10%的采样率下,分别采用本发明方法与现有以高斯随机矩阵作为观测矩阵的方法对测试图像IndianPines进行压缩感知仿真实验,实验结果如图2和图3所示,其中:
图2(a)是测试图像IndianPines第10谱段的原始图像;
图2(b)是采用现有以高斯随机矩阵作为观测矩阵的方法的重构图像,其PSNR为34.8322dB;
图2(c)是采用本发明方法的重构图像,其PSNR为37.3694dB;
图3是不同采样率下两种方法的均方误差曲线。
仿真3:在10%的采样率下,分别采用本发明方法与现有以高斯随机矩阵作为观测矩阵的方法对测试图像Moffet进行压缩感知仿真实验,实验结果如图4和图5所示,其中:
图4(a)是测试图像Moffet第10谱段的原始图像;
图4(b)是采用现有以高斯随机矩阵作为观测矩阵的方法的重构图像,其PSNR为47.2954dB;
图4(c)是采用本发明方法的重构图像,其PSNR为49.9599dB;
图5是不同采样率下两种方法的均方误差曲线。
仿真4:在10%的采样率下,分别采用本发明方法与现有以高斯随机矩阵作为观测矩阵的方法对测试图像WashtonDC进行压缩感知仿真实验,实验结果如图6和图7所示,其中:
图6(a)是测试图像WashtonDC第10谱段的原始图像;
图6(b)是采用现有以高斯随机矩阵作为观测矩阵的方法的重构图像,其PSNR为44.1374dB;
图6(c)是采用本发明方法的重构图像,其PSNR为46.4503dB;
图7是不同采样率下两种方法的均方误差曲线。
从图2、图4和图6的实验结果可以看出,在相同的采样率下,本发明与现有以高斯随机矩阵作为观测矩阵的方法相比,其PSNR更高,重构效果最好。
从图3、图5和图7的曲线图可以看出,随着采样率的提高,两种方法的均方误差均呈现下降趋势;但在相同采样率下,本发明的方法的所恢复的图像的均方误差更小,说明本发明方法的优越性。
- 还没有人留言评论。精彩留言会获得点赞!