光学跟踪系统及光学跟踪系统的标记部姿势及位置算出方法与流程

本发明涉及光学跟踪系统及光学跟踪系统的标记部姿势及位置算出方法，更详细而言，涉及一种利用图案信息的光学跟踪系统及光学跟踪系统的标记部姿势及位置算出方法。

背景技术：

一般而言，为了追踪预定物体的位置，使用光学跟踪系统(optical tracking system)。例如，所述光学跟踪系统可以在诸如手术机器人的装备中，用于实时跟踪标的物。

所述光学跟踪系统通常包括附着于标的物的多个标记和使由所述标记释放的光成像的成像单元，在数学上计算从所述成像单元获得的信息，获得位置信息等。

但是，以往的光学跟踪系统包括多个标记，因而存在装备的大小变大的缺点，因此，对于小型的要求精密性的跟踪而言，可能会不适合。

因此，要求一种能够在简化标记的同时，准确、容易地进行跟踪的光学跟踪系统。

技术实现要素：

解决的技术问题

因此，本发明要解决的课题是提供一种能够在简化标记的同时，准确、容易地进行跟踪的光学跟踪系统。

本发明要解决的另一课题是提供一种能够应用于所述光学跟踪系统的光学跟踪系统的标记部姿势及位置算出方法。

技术方案

本发明示例性的一个实施例的光学跟踪系统包括：标记(marker)部，其包括具有特定信息的图案(pattern)及从所述图案隔开配置且具有第1焦距的第1透镜；第1成像部，其包括具有第2焦距的第2透镜及第1成像单元，所述第1成像单元从所述第2透镜隔开配置，借助于所述第1透镜和所述第2透镜而成像所述图案的第1图像；第2成像部，其包括具有第3焦距的第3透镜及第2成像单元，所述第2成像单元从所述第3透镜隔开配置，借助于所述第1透镜和所述第3透镜而成像所述图案的第2图像；及处理部，其从所述图案的图案面上的坐标与所述图案的第1图像上的第1像素坐标之间的第1坐标变换式及包括所述第1像素坐标与所述图案的第2图像上的第2像素坐标之间的旋转变换在内的所述图案的图案面上的坐标与所述图案的第2图像上的第2像素坐标之间的第2坐标变换式，决定所述标记部的姿势，跟踪所述标记部。

作为一个实施例，所述处理部可以获得如下矩阵：第1变换矩阵，其把与所述图案的图案面上的坐标相应的第1坐标变换成，与所述标记部的对于所述第1透镜的三维坐标相应的第2坐标；第2变换矩阵，其把与所述第2坐标的对于所述第2透镜的三维坐标相应的第3坐标变换成，与所述第1成像部的所述图案的第1图像上的第1像素坐标相应的第4坐标；第3变换矩阵，其把与所述图案的图案面上的坐标相应的第5坐标变换成，与所述标记部的对于所述第1透镜的三维坐标相应的第6坐标，其与所述第1变换矩阵相同；及第4变换矩阵，其把与所述第6坐标的对于所述第3透镜的三维坐标相应的第7坐标变换成，与所述第2成像部的所述图案的第2图像上的第2像素坐标相应的第8坐标；所述第1坐标变换式定义为包括所述第1变换矩阵及所述第2变换矩阵，把所述第1坐标变换成，所述第4坐标，所述第2坐标变换式定义为包含所述第3变换矩阵及所述第4变换矩阵，把所述第5坐标定义为所述第8坐标，所述处理部可以从所述第1及第2坐标变换式，获得定义所述标记部相对于所述第1成像部的姿势的第1姿势定义矩阵。

例如，所述第1坐标变换式可以根据下述数学式定义：

((lu,lv)为所述第1坐标，(lu’,lv’)为所述第4坐标，[C]为所述第1变换矩阵，[A_l]为所述第2变换矩阵，[R_L]为所述第1姿势定义矩阵，s为比例常数)

所述第2坐标变换式可以根据下述数学式定义：

((ru,rv)为所述第5坐标，(ru',rv')为所述第8坐标，[C]为与所述第1变换矩阵相同的所述第3变换矩阵，[A_r]为所述第4变换矩阵，[R_R]为定义所述标记部相对于所述第2成像部的姿势的第2姿势定义矩阵，[R_LR]为定义所述第1成像部相对于所述第2成像部的姿势的第3姿势定义矩阵，s为比例常数)

例如，所述第1变换矩阵及所述第3变换矩阵可以根据下述数学式定义：

((u_c,v_c)为所述图案的中心的坐标，f_b为所述第1焦距)

所述第2及第4变换矩阵可以根据下述数学式定义：

((u'_c,v'_c)为与所述图案的中心对应的所述图案的图像上的像素坐标，f_c在所述第2变换矩阵时为所述第2焦距，在所述第4变换矩阵时为所述第3焦距，pw在所述第2变换矩阵时为所述图案的第1图像的像素宽度，在所述第4变换矩阵时为所述图案的第2图像的像素宽度，ph在所述第2变换矩阵时为所述图案的第1图像的像素高度，在所述第4变换矩阵时为所述图案的第2图像的像素高度)

作为一个实施例，所述处理部从至少3个以上的拍摄图像获得u_c、v_c及f_b的校准值，从而可以获得所述第1变换矩阵及所述第3变换矩阵，利用所述获得的数据，获得f_c、pw、ph的校准值，从而可以获得所述第2变换矩阵及所述第4变换矩阵。

作为一个实施例，所述处理部可以获得对于所述第1坐标和所述第4坐标的多个数据及对于所述第5坐标和所述第8坐标的多个数据，可以根据应用了所述获得的多个数据的下述数学式，获得所述第1姿势定义矩阵：

((lu₁,lv₁),…,(lu_n,lv_n)为所述第1坐标的数据，(lu'₁,lv'₁),…,(lu'_n,lv'_n)为所述第4坐标的数据，(lu'_c,lv'_c)为与所述图案的中心对应的所述图案的第1图像上的像素坐标，((ru₁,rv₁),…,(ru_n,rv_n)为所述第5坐标的数据，(ru'₁,rv'₁),…,(ru'_n,rv'_n)为所述第8坐标的数据，(ru'_c,rv'_c)为与所述图案的中心对应的所述图案的第2图像上的像素坐标)

作为一个实施例，所述处理部可以从对于所述第2坐标和所述第4坐标的第3坐标变换式及对于所述第6坐标和所述第8坐标的第4坐标变换式，决定所述标记部的位置，利用决定的所述标记部的位置，跟踪所述标记部。

例如，所述第3坐标变换式可以根据下述数学式定义：

((u'₁,v'₁)为所述第4坐标，(X,Y,Z)为所述第2坐标，[A_L]为所述第2变换矩阵，[I]为3x3形态的恒等矩阵(identity matrix)，[0]为3x1形态的零矩阵，s为比例常数)

所述第4坐标变换式可以根据下述数学式定义：

((u'₂,v'₂)为所述第8坐标，(X,Y,Z)为所述第6坐标，[AR]为所述第4变换矩阵，[RLR]为3x3形态的所述第3姿势定义矩阵，[T]为3x1形态的位置变换矩阵，s为比例常数)

作为一个实施例，所述处理部可以获得在所述第1及第2成像单元分别拍摄的作为所述图案视野范围中心的第1中心坐标及第2中心坐标，利用所述获得的多个中心坐标，可以校准所述第1成像部及所述第2成像部之间的位置变换矩阵，利用所述校准的位置变换矩阵，可以获得所述标记部的位置。

作为一个实施例，所述处理部可以在至少2个以上的位置测量所述标记部并获得换算系数，一同利用所述获得的换算系数和所述获得的多个中心坐标，可以校准所述第1成像部及所述第2成像部之间的所述位置变换矩阵。

本发明示例性的一个实施例的光学跟踪系统的标记部姿势及位置算出方法，提供用于算出所述标记部的姿势，以便跟踪所述标记部，所述光学跟踪系统包括：标记(marker)部，其包括具有特定信息的图案(pattern)及从所述图案隔开配置且具有第1焦距的第1透镜；第1成像部，其包括具有第2焦距的第2透镜及第1成像单元，所述第1成像单元从所述第2透镜隔开配置，借助于所述第1透镜和所述第2透镜而成像所述图案的第1图像；及具有第3焦距的第3透镜及第2成像单元，所述第2成像单元从所述第3透镜隔开配置，借助于所述第1透镜和所述第3透镜而成像所述图案的第2图像。所述光学跟踪系统的标记部姿势及位置算出方法包括：获得如下矩阵的步骤，即，第1变换矩阵，其把与所述图案的图案面上的坐标相应的第1坐标变换成，与所述标记部的对于所述第1透镜的三维坐标相应的第2坐标；第2变换矩阵，其把与所述第2坐标的对于所述第2透镜的三维坐标相应的第3坐标变换成，与所述第1成像部的所述图案的第1图像上的第1像素坐标相应的第4坐标；第3变换矩阵，其把与所述图案的图案面上的坐标相应的第5坐标变换成，与所述标记部的对于所述第1透镜的三维坐标相应的第6坐标，其与所述第1变换矩阵相同；及第4变换矩阵，其把与所述第6坐标的对于所述第3透镜的三维坐标相应的第7坐标变换成，与所述第2成像部的所述图案的第2图像上的第2像素坐标相应的第8坐标；及获得姿势定义矩阵的步骤，从第1坐标变换式及第2坐标变换式获得定义所述标记部的姿势的姿势定义矩阵，所述第1坐标变换式包括所述第1变换矩阵及所述第2变换矩阵，把所述第1坐标变换成所述第4坐标，所述第2坐标变换式包括所述第3变换矩阵及所述第4变换矩阵，把所述第5坐标变换成所述第8坐标。

作为一个实施例，所述光学跟踪系统的标记部姿势及位置算出方法可以还包括：获得在所述第1及第2成像单元分别拍摄的作为所述图案的视野范围中心的第1中心坐标及第2中心坐标的步骤；利用所述获得的多个中心坐标，校准所述第1成像部及所述第2成像部之间的位置变换矩阵的步骤；及利用所述校准的位置变换矩阵获得所述标记部的位置的步骤。

作为一个实施例，所述光学跟踪系统的标记部姿势及位置算出方法在所述校准位置变换矩阵的步骤之前，可以还包括在至少2个以上位置测量所述标记部而获得换算系数的步骤；在校准位置变换矩阵的步骤中，一同利用所述获得的换算系数和所述获得的多个中心坐标，可以校准所述第1成像部及所述第2成像部之间的位置变换矩阵。

发明效果

根据本发明，在跟踪标记部的光学跟踪系统中，标记部包含特定信息的图案，以便能够跟踪，可以实现标记部小型化，利用坐标变换式对所述标记部和所述成像部的光学系进行建模，立体构成所述光学系，从而能够更准确地决定所述标记部的姿势及位置，因而能够以更单纯容易的方法，更准确地跟踪标记部。

另外，应用立体方式，对包含特定信息的图案并小型化的标记部进行建模，从而能够更准确地决定所述标记部的位置，因而能够以更单纯容易的方法实现准确的标记部跟踪。

附图说明

图1是图示本发明一个实施例的光学跟踪系统的概念图。

图2是概略性地显示图1的光学跟踪系统的处理部为了决定标记部的姿势所需的解题过程的流程图。

图3是显示在图2的解题过程中进行系统建模的过程的流程图。

图4是用于说明图3的进行系统建模的过程的概念图。

图5是显示在图2的解题过程中校准第2变换矩阵的过程的流程图。

图6是显示在图2的解题过程中校准第1变换矩阵的过程的流程图。

图7是显示在图2的解题过程中获得姿势定义矩阵的过程的一个示例的流程图。

图8是显示在图2的解题过程中获得姿势定义矩阵的过程的另一示例的流程图。

图9是显示本发明一个实施例的光学跟踪系统的标记部姿势算出方法的流程图。

图10是图示本发明另一实施例的光学跟踪系统的概念图。

图11是概略性地显示图10的光学跟踪系统的处理部为了决定标记部的姿势所需的解题过程的流程图。

图12是显示在图11的解题过程中校准变换矩阵的过程的流程图。

图13是显示在图11的解题过程中获得姿势定义矩阵的过程的一个示例的流程图。

图14是显示本发明另一实施例的光学跟踪系统的标记部姿势算出方法的流程图。

图15是概略性地显示图10的光学跟踪系统的处理部为了决定标记部的位置所需的解题过程的流程图。

图16是用于说明在图15的解题过程中执行系统建模的过程的概念图。

图17是显示在图15的解题过程中校准位置变换矩阵的过程的流程图。

图18是显示在图15的解题过程中获得标记部的位置的过程的一个示例的流程图。

图19是显示在图15的解题过程中获得标记部的位置的过程的另一示例的流程图。

图20是显示本发明一个实施例的光学跟踪系统的标记部位置算出方法的流程图。

具体实施方式

本发明可以具有多样的变更，可以具有多种形态，在附图中示例性列举特定实施例并在正文中详细说明。但是，这并非用于将本发明限定于特定的公开形态，应理解为包括本发明的思想及技术范围内包含的所有变更、等同物乃至替代物。

第1、第2等术语可以用于说明多样的构成要素，但所述构成要素不得由所述术语限定。所述术语只用于把一种构成要素区别于其它构成要素之目的。例如，在不超出本发明的权利范围的同时，第1构成要素可以命名为第2构成要素，类似地，第2构成要素也可以命名为第1构成要素。

本申请中使用的术语只用于说明特定的实施例，并非要限定本发明之意图。只要在文理上未明确表示不同，则单数的表现也包括复数的表现。在本申请中，“包括”或“具有”等术语应理解为是要指定说明书中记载的特征、数字、步骤、动作、构成要素、部件或其组合的存在，不预先排除一个或其以上的其它特征或数字、步骤、动作、构成要素、部件或其组合的存在或附加可能性。

只要未不同地定义，包括技术性或科学性术语在内，在此使用的所有术语具有与本发明所属技术领域的普通技术人员一般理解的意义相同的意义。

与普遍使用的字典中定义的内容相同的术语，应解释为具有与相关技术文理上具有的意义一致的意义，只要在本申请中未明确定义，则不得解释为理想地或过度形式上的意义。

下面参照附图，更详细地说明本发明的优选实施例。

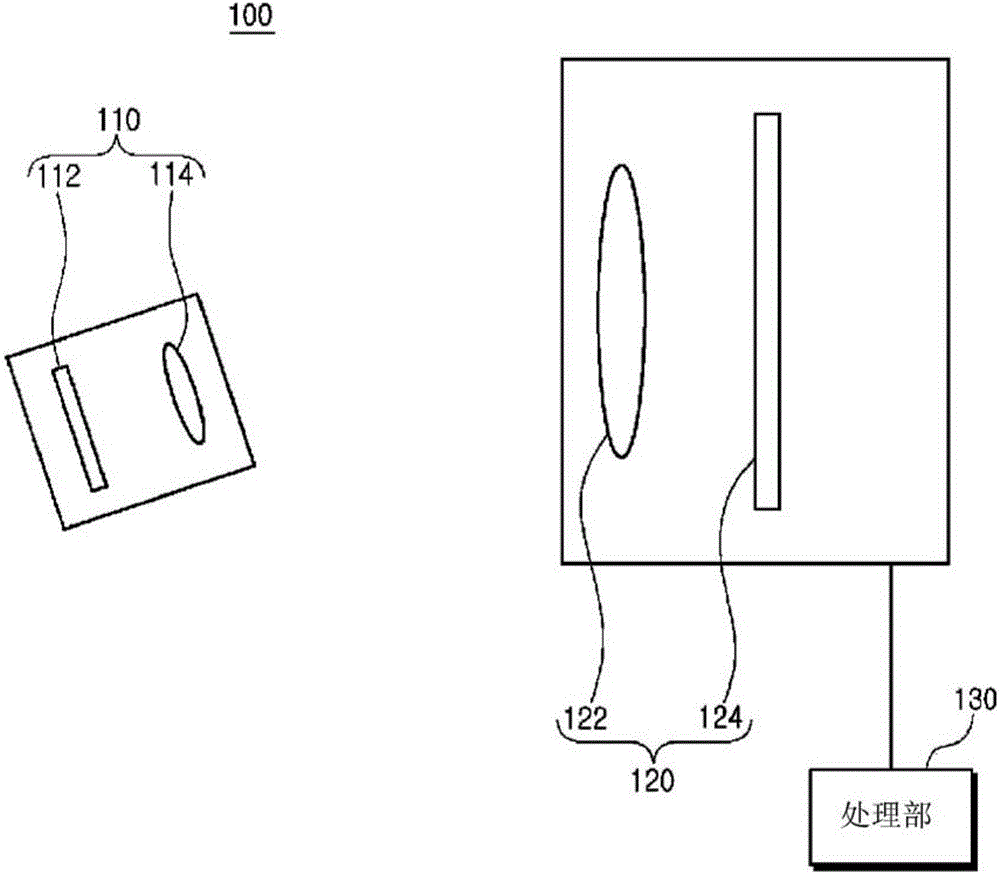
图1是图示本发明一个实施例的光学跟踪系统的概念图。

如果参照图1，本发明示例性的一个实施例的光学跟踪系统100包括标记(marker)部110、成像部120及处理部130。

所述标记部110包括图案(pattern)112及第1透镜114。

所述图案112具有特定信息。例如，所述特定信息是所述图案作为后述成像部120为了跟踪而能够识别的信息，可以包括与条形码(bar code)类似的一维图案、与QR码(QR code)类似的二维图案等。

所述第1透镜114从所述图案112隔开配置，具有第1焦距。例如，所述第1透镜114与所述图案112之间的隔开距离可以与所述第1透镜114的第1焦距相同，以便后述的成像部120远距离也可以对所述图案112进行成像并跟踪。此时，通过所述第1透镜114的对于所述图案112的光束(bundle of rays)可以实现平行。所述第1透镜114例如可以执行与显微镜的物镜类似的功能。

所述标记部110可以不包括光源，此时，所述标记部110可以使用利用位于外部的照明的被动标记(passive marker)。不同于此，所述标记部110也可以包括光源，此时，所述标记部110可以使用利用自身照明的主动标记(active marker)。

所述成像部120包括第2透镜122及成像单元124。

所述第2透镜122具有第2焦距。所述第2透镜114例如可以执行与显微镜的目镜类似的功能。

所述成像单元124从所述第2透镜122隔开配置，借助于所述第1透镜114和所述第2透镜122而成像所述图案112的图像。例如，所述成像单元124与所述第2透镜122之间的隔开距离可以与所述第2透镜122的第2焦距相同，以便可以使通过所述第1透镜114的实现平行的对于所述图案112的光束成像。例如，所述成像单元124可以包括诸如CCD(charge coupled device)、CMOS(complementary metal-oxide semiconductor)等的图像传感器。

所述处理部130从所述图案112的图案面上的坐标与所述图案112的图像上的像素坐标之间的坐标变换式来决定所述标记部110的姿势。所述处理部130利用决定的所述标记部110的姿势，跟踪所述标记部110。所述处理部130例如可以包括计算机，或更具体而言，可以包括中央处理装置(CPU)。

下面参照附图，更详细地说明成为所述处理部130的功能依据的系统建模过程及据此决定所述标记部110的姿势的过程。

图2是概略性地显示图1的光学跟踪系统的处理部为了决定标记部的姿势所需的解题过程的流程图。

如果参照图2，首先对具有所述构成的所述光学跟踪系统100执行系统建模(S100)。

在如图1所示的光学跟踪系统100中，所述图案112的图案面上的坐标与所述图案112的图像上的像素坐标之间的坐标变换借助于所述光学跟踪系统100的光学系而实现，因而对由所述光学跟踪系统100的光学系决定的坐标变换进行建模，从而可以设置所述坐标变换式。此时，由所述光学跟踪系统100的光学系决定的坐标变换，可以根据所述标记部110及所述成像部120各个光学系及它们之间的关系进行建模。

接着，在作为系统建模的结果而获得的坐标变换式中，对后述第1及第2变换矩阵进行校准(calibration)(S200)。

当分别把图1所示的所述图案112的图案面上的坐标定义为第1坐标、把所述第1坐标的对于所述第1透镜114的三维本地性坐标定义为第2坐标、把所述第2坐标的对于所述第2透镜122的三维本地性坐标定义为第3坐标、把所述成像部120的所述图案112的图像上的像素坐标定义为第4坐标时，所述第1变换矩阵是把所述第1坐标变换成所述第2坐标的矩阵，所述第2变换矩阵是把所述第3坐标变换成所述第4坐标的矩阵。

作为所述系统建模的结果而获得的坐标变换式虽然以对于图1所示的所述标记部110及所述成像部120的光学系的各种参数的公式进行确定，但由于可能无法准确获得所述参数或值可能会因机构的配置状态等而使值发生变化，因而通过校准所述第1及第2变换矩阵，从而能够进行更准确的系统建模。

接下来，利用校准结果获得姿势定义矩阵(S300)。

其中，姿势意味着所述标记部110朝向的方向，所述姿势定义矩阵作为提供对于所述标记部110的姿势的信息的矩阵，可以从所述姿势定义矩阵掌握所述标记部110的翻滚角(roll)、俯仰角(pitch)、偏航角(yaw)等。

下面，针对图2所示各步骤，以附图为参照更具体地说明。

图3是显示在图2的解题过程中进行系统建模的过程的流程图，图4是用于说明进行图3的系统建模的过程的概念图。

如果参照图3及图4，首先，获得由所述标记部110与所述成像部120之间的光路径决定的3条直线的方程式(S110)。

具体而言，把所述第1透镜114的中心点称为第1中心点A，把所述第2透镜122的中心点称为第2中心点O，把所述图案112上的任意点称为B。对于所述任意点B的光通过所述第1透镜114的第1中心点A后直行，把通过所述第1中心点A的光与所述第2透镜122相交的点称为D，把在所述D点被所述第2透镜122折射而在所述成像单元124成像的点称为E。另外，经过所述第1透镜114的第1中心点A并通过所述第2透镜122的第2中心点O的光直行，把该光与线段DE的延长线相交的点称为C。

此时，如图4所示，把对于线段AO(或线段AC)的直线方程式、对于线段AD的直线方程式及对于线段DC的直线方程式分别定义为L1、L2及L3。

在世界坐标系(world coordinate system)中，所述第1中心点A的坐标设置为(X,Y,Z)，所述第2中心点O的坐标设置为作为原点的(0,0,0)。由于把所述第2透镜122的第2中心点O的坐标设置为原点，因而对于所述第2透镜122的三维本地性坐标系与所述世界坐标系相同。

另外，把所述图案112上的任意点(对应于B点)的坐标定为(u,v)，把所述图案112的中心点的坐标定为(u_c,v_c)，把在所述成像单元124成像的所述图案112的图像的像素(对应于E点)的坐标定为(u’,v’)。作为一个示例，所述坐标(u,v)、(u_c,v_c)可以以所述图案112的左上侧为基准进行设置，作为一个示例，所述坐标(u’,v’)可以以所述图案112的图像的左上侧为基准进行设置。

另一方面，如果使所述成像单元124位于所述第2透镜122的焦距f_c，则所述成像单元124的z轴坐标为-f_c。

利用以上的信息，依次获得所述三个直线方程式。

直线L1的方程式从线段AO求出，在此获得C点的位置。直线L2的方程式从线段AB求出，在此获得D点的位置。直线L3的方程式从线段DC求出。此时，由于已知A点和O点的世界坐标，因而只要知道B点的世界坐标，则可知所述三个直线的方程式。

如果把定义所述标记部110的姿势的姿势定义矩阵定义为3*3矩阵[R]，把矩阵[R]的各成分分别定义为r₁₁、r₁₂、r₁₃、r₂₁、r₂₂、r₂₃、r₃₁、r₃₂、r₃₃，那么，B点的世界坐标可以把B点的图案上坐标(u,v)确定为以矩阵[R]和所述第1透镜114的焦距f_b为基础变换的(r₁₁u+r₁₂v+r₁₃f_b+X，r₂₁u+r₂₂v+r₂₃f_b+Y，r₃₁u+r₃₂v+r₃₃f_b+Z)。

因此，可以从A点、O点及B点的世界坐标获得三个直线方程式。

接着，从所述获得的三个直线方程式导出所述图案112及图案的图像之间的关系式(S120)。

在前面求出的直线L3的方程式中，可以获得E点的位置(E点的世界坐标)，因此，由此可知E点的像素坐标(u’,v’)。

因此，可以用B点的图案上坐标(u,v)表示E点的像素坐标(u’,v’)，因此，可以确定与B点对应的所述图案112及与E点对应的图案的图像之间的关系式。

接下来，把所述关系式表现为矩阵方程式，设置为所述坐标变换式(S130)。

所述关系式可以以诸如下述数学式1的矩阵方程式表现，可以把这种对于坐标变换的矩阵方程式设置为所述坐标变换式。

(数学式1)

其中，(u,v)意味着所述第1坐标，(u’,v’)意味着所述第4坐标，[C]意味着所述第1变换矩阵，[A]意味着所述第2变换矩阵，而且，[R]意味着所述姿势定义矩阵。另外，(u_c,v_c)意味着所述图案的中心的图案面上的坐标，f_b意味着所述第1焦距，f_c意味着所述第2焦距，pw意味着所述图案的图像的像素宽度，ph意味着所述图案的图像的像素高度。另外，在(u_i,v_i)、(u’_i,v’_i)中，i意味着预定的第i号图案。

可知，所述坐标变换式由图1中说明的所述第1及第2变换矩阵及所述姿势定义矩阵之积构成。

具体而言，如果从概念上考查所述坐标变换式，那么，如在图1中所作的说明，当分别把所述图案112的图案面上的坐标定义为第1坐标((u,v))、把所述第1坐标的对于所述第1透镜114的三维性本地坐标定义为第2坐标、把所述第2坐标的对于所述第2透镜122的三维本地性坐标(与世界坐标相同)定义为第3坐标、把所述成像部120的所述图案112的图像上的像素坐标定义为第4坐标((u’,v’))时，可知所述坐标变换式由把所述第1坐标变换成所述第2坐标的第1变换矩阵[C]、把所述第2坐标变换成所述第3坐标的姿势定义矩阵[R]及把所述第3坐标变换成所述第4坐标的第2变换矩阵[A]之积的[A][R][C]代表。

下面以附图为参照，对作为所述系统建模的结果而获得的坐标变换式中校准所述第1及第2变换矩阵的过程(S200)进行更详细说明。

所述校准先针对所述第2变换矩阵执行，然后针对所述第1变换矩阵进行。

图5是显示在图2的解题过程中校准第2变换矩阵的过程的流程图。

如果参照图5，首先定义矩阵[B]和矩阵[H]，以便容易进行校准所需的数学解析(S210)。

具体而言，如果利用所述第2变换矩阵([A])定义矩阵[B]，则如数学式2所示，如果利用所述第1变换矩阵([C])、所述第2变换矩阵([A])及所述姿势定义矩阵([R])定义矩阵[H]，则如数学式3所示。

(数学式2)

[B]＝[A]^-T＊[A]^-1

(数学式3)

[H]＝[A][R][C]

其中，各矩阵[A]、[B]、[C]、[H]、[R]均具有3*3形态，可以表示为[H]＝[h₁,h₂,h₃]，[R]＝[r₁,r₂,r₃]。

如果在数学式3的两边乘以A^-1，则获得数学式4。

(数学式4)

A^-1[h₁h₂h₃]＝[r₁r₂T]

接着，利用矩阵[R]的规范正交性(orthonormality)，设置由[H]和[B]的成分构成的方程式(S220)。

具体而言，如果利用与旋转矩阵(rotation matrix)相应的姿势定义矩阵([R])的规范正交性，则可以如数学式5所示定义矩阵[B]。

(数学式5)

其中，α＝-f_c/pw，β＝-f_c/ph，f_c意味着所述成像部120的第2透镜122的焦距，pw和ph分别意味着像素宽度和高度。

利用矩阵[B]的非0的成分，如数学式6所示定义列向量b和v_ij。

(数学式6)

b＝[B₁₁ B₂₂ B₁₃ B₂₃ B₃₃]^T

v_ij＝[h_i1h_j1，h_i2h_j2，h_i3h_j1+h_i1h_j3，h_i3h_j2+h_i2h_j3，h_i3h_j3]^T

在数学式6中，如果利用矩阵[R]的规范正交性，则可以获得数学式7。

(数学式7)

然后，把3张以上的影像数据应用于[H]，求出[B]的解(S230)。

具体而言，把至少3张以上的影像应用于数学式7后，作为一个示例，可以利用诸如奇异值分解(singular value decomposition，SVD)的方法，求出列向量b。如果求出列向量b，则可知矩阵[B]的所有成分。

接着，获得最终校准的[A](S240)。

具体而言，如果知道矩阵[B]的所有成分，则可通过下述数学式8而求出v′_c、α、β、u′_c(把λ、γ表现为参数)。

(数学式8)

γ＝-B₁₂α²β/λ

因此，从数学式9可知矩阵[A]的所有成分。

(数学式9)

然后，利用前面校准的第2变换矩阵([A])，校准第1变换矩阵([C])。

图6是显示在图2的解题过程中校准第1变换矩阵的过程的流程图。

如果参照图6，把先校准的矩阵[A]代入矩阵[H]并整理，获得矩阵[R](S250)。

具体而言，把数学式9的所述第2变换矩阵[A]代入数学式3，整理数学式1的[R][C]，获得数学式10。

(数学式10)

在数学式10中，如果把矩阵[R]放入[R]＝[r₁r₂r₃]，则[R]可以在数学式11中按列向量成分而获得。

(数学式11)

r₁＝[A]^-1h₁，r₂＝[A]^-1h₂，r₃＝r₁×r₂

接着，把矩阵[HK]定义为[HK]＝[A][R]，代入所述坐标变换式并整理(S260)。

具体而言，把矩阵[A]与矩阵[R]之积定义为矩阵[HK]，代入数学式1的坐标变换式并整理，使得由矩阵[HK]和矩阵[C]的成分构成。

此时，利用数学式9中求出的矩阵[A]和数学式11中求出的矩阵[R]，可以求出矩阵[HK]，如果将其应用于数学式1的坐标变换式，则获得由矩阵[HK]和矩阵[C]的成分构成的数学式12。

(数学式12)

然后，把整理的公式变形为[AA][CC]＝[BB]形态(S270)。

具体而言，在整理的公式中，把只由矩阵[C]的成分构成的矩阵定义为[CC]并分离后，把整理的公式变形为[AA][CC]＝[BB]形态。此时，由于已知矩阵[HK]，因而利用矩阵[HK]，可以如数学式13所示定义矩阵[AA]、矩阵[BB]及矩阵[CC]。

(数学式13)

接着，从[CC]＝[AA]^-1[BB]求出[CC]，获得校准的矩阵[C](S280)。

具体而言，从对公式[AA][CC]＝[BB]进行变形的[CC]＝[AA]^-1[BB]获得[CC]的成分，获得最终校准的所述第1变换矩阵[C]。

下面，以附图为参照，更详细说明利用所述校准的第1及第2变换矩阵而获得所述姿势定义矩阵的过程(S300)。

图7是显示在图2的解题过程中获得姿势定义矩阵的过程的一个示例的流程图。

如果参照图7，作为获得所述姿势定义矩阵[R]的一个示例，首先，设置在两边对自己自身进行外积的方程式(S310)。

具体而言，如果在所述数学式1的两边对自己自身进行外积，则为0，因此，如果将其设置为方程式，则可获得数学式14。

(数学式14)

接着，作为一个示例，利用诸如奇异值分解(SVD)的方法获得矩阵[H](S320a)。

具体而言，把数学式3的[H]＝[A][R][C]应用于数学式14后，整理成对于矩阵[H]的各成分(H1,H2,…,H9)的方程式，获得了数学式15。

(数学式15)

作为一个示例，利用诸如奇异值分解(SVD)的方法，获得数学式15的2n个公式。

然后，从[R]＝[A]^-1[H][C]^-1获得[R](S330a)。

具体而言，从对数学式3的[H]＝[A][R][C]进行变形的[R]＝[A]^-1[H][C]^-1获得[R]。

所述姿势定义矩阵也可以以其它方法获得。

图8是显示在图2的解题过程中获得姿势定义矩阵的过程的另一示例的流程图。

如果参照图8，作为获得所述姿势定义矩阵[R]的另一示例，首先设置在两边对自己自身进行外积的方程式(S310)。本过程与图7的过程相同，因而省略重复的说明。

接着，整理成对于r11～r33的方程式(S320b)。

具体而言，从数学式14整理成对于所述姿势定义矩阵[R]的各成分r₁₁、r₁₂、r₁₃、r₂₁、r₂₂、r₂₃、r₃₁、r₃₂、r₃₃的方程式，获得数学式16。

(数学式16)

然后，作为一个示例，利用诸如奇异值分解(SVD)的方法，获得矩阵[R](S330b)。

具体而言，利用诸如奇异值分解(SVD)的方法，获得数学式16的2n个公式。

如上所述，最终可以获得所述姿势定义矩阵[R]。

把如上所述的系统建模过程及姿势定义矩阵[R]的获得方法应用于图1所示的所述光学跟踪系统100，可以算出所述标记部110的姿势。

下面，以附图为参照，更详细地说明所述处理部130算出所述标记部110的姿势的方法。

图9是显示本发明一个实施例的光学跟踪系统的标记部姿势算出方法的流程图。

如果参照图9，首先，所述处理部130从至少3个影像校准第1及第2变换矩阵(S510)。

所述校准实质上与图2中说明的步骤S200、图5及图6中具体说明的步骤S210至步骤S280的过程相同，在所述处理部130中，如所述过程中的步骤S230和步骤S280所示，只利用校准所需的最终方程式，便可以校准所述第1及第2变换矩阵。

然后，从包括所述第1及第2变换矩阵的坐标变换式获得姿势定义矩阵(S520)。

所述姿势定义矩阵的获得实质上与图2中说明的步骤S300、图7及图8中具体说明的步骤S310至步骤S330a以及步骤S310至步骤S330b的过程相同，在所述处理部130中，如所述过程中的步骤S320a和S320a或步骤S320b所示，只利用所述姿势定义矩阵获得所需的最终方程式，便可以获得所述姿势定义矩阵。

因此，所述处理部130事先校准而预先获得把所述第1坐标变换成所述第2坐标的第1变换矩阵及把所述第3坐标变换成所述第4坐标的第2变换矩阵后，可以从所述坐标变换式获得定义所述标记部110的姿势的姿势定义矩阵。

如果获得所述姿势定义矩阵，则可知所述标记部110的姿势。例如，可以从所述姿势定义矩阵掌握所述标记部110的翻滚角(roll)、俯仰角(pitch)、偏航角(yaw)等。

根据如上所述的光学跟踪系统，标记部包括特定信息的图案而使得能够跟踪，可以实现标记部小型化，利用坐标变换式，对所述标记部和所述成像部的光学系进行建模，从而能够决定所述标记部的姿势，因而能够以更单纯容易的方法，实现准确的标记部跟踪。

图10是图示本发明另一实施例的光学跟踪系统的概念图。

如果参照图10，本发明另一实施例的光学跟踪系统1000包括标记部1110、第1成像部1120a、第2成像部1120b及处理部1130。

图10所示的光学跟踪系统1000除了应用包括两个成像部的立体方式及处理部1140利用两个成像部来决定姿势之外，实质上与图1所示的光学跟踪系统100相同，因而省略重复的详细说明。

所述标记部1110包括图案(pattern)1112及第1透镜1114，实质上与图1所示的标记部110相同。

所述第1成像部1120a包括具有第2焦距的第2透镜及第1成像单元，所述第1成像单元从所述第2透镜隔开配置，借助于所述第1透镜和所述第2透镜而成像所述图案的第1图像。

所述第2成像部1120b包括具有第3焦距的第3透镜及第2成像单元，所述第2成像单元从所述第3透镜隔开配置，借助于所述第1透镜和所述第3透镜而成像所述图案的第2图像。

所述第1成像部1120a及所述第2成像部1120b实质上分别与图1所示的成像部120相同。

所述处理部1130从所述图案1112的图案面上的坐标与所述图案1112的第1图像上的第1像素坐标之间的第1坐标变换式及所述图案1112的图案面上的坐标与所述图案1112的第2图像上的第2像素坐标之间的第2坐标变换式，决定所述标记部1110的姿势。此时，所述第2坐标变换式包括所述第1像素坐标与所述第2图像上的第2像素坐标之间的旋转变换。所述处理部1130利用决定的所述标记部1110姿势，跟踪所述标记部1110。

下面以附图以参照，详细说明成为所述处理部1130功能的根据的系统建模过程及据此决定所述标记部1110的姿势的过程。

图11是概略性显示图10的光学跟踪系统的处理部为了决定标记部的姿势所需的解题过程的流程图。

如果参照图11，首先，对具有上述构成的所述光学跟踪系统1000进行系统建模(S1100)。

在如图10所示的光学跟踪系统1000中，所述图案1112的图案面上的坐标与所述图案1112的图像上的像素坐标之间的坐标变换，借助于所述光学跟踪系统1100的光学系而实现，因而通过对由所述光学跟踪系统1000的光学系决定的坐标变换进行建模，从而可以设置所述坐标变换式。此时，由所述光学跟踪系统100的光学系决定的坐标变换可以根据所述标记部1110及所述第1及第2成像部1120a、1120b各个的光学系及它们之间的关系而建模。

接着，在作为系统建模的结果而获得的坐标变换式中，校准后述的第1、第2、第3及第4变换矩阵(S1200)。

当分别把图10所示所述图案1112的图案面上的坐标定义为第1坐标、把所述第1坐标的对于所述第1透镜1114的三维本地性坐标定义为第2坐标、把所述第2坐标的对于所述第2透镜1122a的三维本地性坐标定义为第3坐标、把所述第1成像部1120a的所述图案1112的第1图像上的像素坐标定义为第4坐标时，所述第1变换矩阵是把所述第1坐标变换成所述第2坐标的矩阵，所述第2变换矩阵是把所述第3坐标变换成所述第4坐标的矩阵。

另外，当分别把图10所示的所述图案1112的图案面上的坐标定义为第5坐标、把所述第5坐标的对于所述第1透镜1114的三维本地性坐标定义为第6坐标、把所述第6坐标的对于所述第3透镜1122b的三维本地性坐标定义为第7坐标、把所述第2成像部1120b的所述图案1112的第2图像上的像素坐标定义为第8坐标时，所述第3变换矩阵是把所述第5坐标变换成所述第6坐标的矩阵，所述第4变换矩阵是把所述第7坐标变换成所述第8坐标的矩阵。

作为所述系统建模的结果而获得的坐标变换式虽然以对于图10所示的所述标记部1100及所述成像部1120的光学系的各种参数的公式而确定，但由于无法准确获得所述参数或值会因机构的配置状态等而变化，因而通过校准所述第1及第2变换矩阵，可以能更准确系统建模。

然后，利用校准结果获得姿势定义矩阵(S1300)。

所述姿势定义矩阵作为提供对于所述标记部1110的姿势的信息的矩阵，从所述姿势定义矩阵可以掌握所述标记部1110的翻滚角(roll)、俯仰角(pitch)、偏航角(yaw)等。

下面对图11所示的各步骤进行更具体说明。

首先，在执行系统建模(S1100)方面，如图3中说明的方式及结果相同地应用。因此，可以针对所述第1成像部1120a和所述第2成像部1120b，独立地应用数学式1。因此，系统建模结果可以获得下述数学式17。出于便利，在数学式17中，在对于第1成像部1120a的变数中应用L、l，在对于第2成像部1120b的变数中应用R、r。

(数学式17)

其中，(lu,lv)意味着所述第1坐标，(lu',lv')意味着所述第4坐标，[C]意味着所述第1变换矩阵，[A_l]意味着所述第2变换矩阵，[R_L]意味着所述第1姿势定义矩阵，(ru,rv)意味着所述第5坐标，(ru',rv')意味着所述第6坐标，[C]意味着与所述第1变换矩阵相同的所述第3变换矩阵，[A_r]意味着所述第4变换矩阵，[R_R]意味着所述第2姿势定义矩阵。另外，如果参照图10，矩阵[R_R]可以用矩阵[R_LR][R_L]表现。其中，[R_LR]意味着把对于所述第1成像部1120a的三维本地性坐标变换成对于所述第2成像部1120b的三维本地性坐标的矩阵，可以视为定义所述第1成像部1120a相对于所述第2成像部1120b的姿势的矩阵。

下面以附图为参照，更详细说明作为所述系统建模的结果而获得的坐标变换式中校准所述第1、第2、第3及第4变换矩阵的过程(S1200)。

图12是显示在图11的解题过程中校准变换矩阵的过程的流程图。

校准所述变换矩阵的过程基本上与前面在图5及图6中说明的过程相同。

如果参照图12，首先把步骤S210至步骤S240的过程应用于所述第1成像部1120a，校准[A_l](S1210a)。接着，把步骤S250应用于所述第1成像部1120a而获得[R_L](S1220a)。

另外，与此并列，把步骤S210至步骤S240的过程应用于所述第2成像部1120b，校准[A_r](S1210b)。接着，把步骤S250应用于所述第2成像部1120b而获得[R_R](S1220b)。

对于根据如上所述在图5及图6中说明的方式而独立地获得的[A_l]、[R_L]、[A_r]及[R_R]，以与图5及图6中说明的方式类似的方式校准[C]。

具体而言，首先把矩阵[HK_l]定义为[HK_l]＝[A_l][R_L]，把矩阵[HK_r]定义为[HK_r]＝[A_r][R_R]，代入各个坐标变换式并整理(S1260)。该过程对应于图6中说明的步骤S260，由此，获得由矩阵[HK_l]及[HK_r]和矩阵[C]的成分构成的数学式18。

(数学式18)

接着，把整理的公式变形成[AA2][CC2]＝[BB2]形态(S1270)。该过程对应于图6中说明的步骤S270，此时，可以如数学式19所示定义矩阵[AA2]、矩阵[BB2]及矩阵[CC2]。

(数学式19)

接着，从[CC2]＝[AA2]^-1[BB2]求出[CC2]，获得校准的[C]获得(S1280)。该过程对应于图6中说明的步骤S280，从对[AA2][CC2]＝[BB2]进行变形的[CC2]＝[AA2]^-1[BB2]获得[CC2]的成分，获得与最终校准的所述第1变换矩阵及第3变换矩阵相应的[C]。

下面以附图为参照，更详细地说明利用所述校准的第1、第2、第3及第4变换矩阵而获得所述姿势定义矩阵的过程(S1300)。

图13是显示在图11的解题过程中获得姿势定义矩阵的过程的一个示例的流程图。

获得所述姿势定义矩阵的过程基本上与前面在图8中说明的过程相同，但作为立体方式，在利用更多数据方面有差异。

如果参照图13，首先，在所述第1坐标变换式中，把步骤S310及步骤S320b的过程应用于[R_L]，整理成对于成分r11～r33的第1方程式(S1310)。该过程对应于图8中说明的步骤S310及步骤S320b的过程，在下述数学式21中显示出所述第1方程式。

(数学式20)

接着，在所述第2坐标变换式中，把[R_LR]的成分放入r'11～r'33，把步骤S310及步骤S320b的过程应用于[R_L]，整理成对于成分r11～r33的第2方程式(S1320)。该过程应用图8中说明的步骤S310及步骤S320b的过程，在下述数学式21中显示出所述第2方程式。

(数学式21)

接着，把整理的对于r11～r33的所述第1及第2方程式整理成统合方程式(S1330)。由此，获得数学式22。

(数学式22)

接着，作为一个示例，利用诸如奇异值分解(SVD)的方法获得矩阵[R_L](S1340)。

具体而言，在数学式22中，矩阵[LW_i]及[RW_i]分别包括2个公式，因此，针对r11～r33获得共4n个公式，因而可以利用诸如奇异值分解(SVD)的方法而获得。

数学式22包括4n个公式，包括比图1至图9中说明的方法更多的公式，因而可以获得对于矩阵[R_L]的更准确结果，因此，可以实现所述标记部1110的更准确的姿势测量。

下面以附图为参照，更详细地说明所述处理部1130算出所述标记部1110的姿势的方法。

图14是显示本发明另一实施例的光学跟踪系统的标记部姿势算出方法的流程图。

如果参照图14，首先，所述处理部1130从至少3个影像校准第1、第2、第3及第4变换矩阵(S1510)。

所述校准实质上与图11中说明的步骤S1200、图12中具体说明的步骤S1210a及S1210b至步骤S1280的过程相同，在所述处理部1130中，如所述过程中的步骤S1210a、S1220a、S1210b、S1220b及步骤S1280等所示，只利用校准所需的最终方程式，便能够校准所述第1及第2变换矩阵。

然后，从包括所述第1、第2、第3及第4变换矩阵的第1及第2坐标变换式获得姿势定义矩阵(S1520)。

所述姿势定义矩阵的获得实质上与图11中说明的步骤S1300、图13中具体说明的步骤S1310至步骤S1340的过程相同，在所述处理部1130中，如所述过程中的步骤S1330及步骤S1340所示，只利用获得所述姿势定义矩阵所需的最终方程式，便能够获得所述姿势定义矩阵。

因此，所述处理部1130事先校准而预先获得把所述第1坐标变换成所述第2坐标的第1变换矩阵、把所述第3坐标变换成所述第4坐标的第2变换矩阵、把所述第5坐标变换成所述第6坐标的第3变换矩阵及把所述第7坐标变换成所述第8坐标的第4变换矩阵后，可以从所述第1及第2坐标变换式获得定义所述标记部1110的姿势的姿势定义矩阵。

如果获得所述姿势定义矩阵，则可知所述标记部1110的姿势。例如，从所述姿势定义矩阵可以掌握所述标记部1110的翻滚角(roll)、俯仰角(pitch)、偏航角(yaw)等。

根据如上所述的光学跟踪系统，就跟踪标记部的光学跟踪系统而言，标记部包括特定信息的图案而使得能够实现跟踪，可以实现标记部小型化，以坐标变换式对所述标记部和所述成像部的光学系进行建模，且应用立体方式，从而能够更准确地决定所述标记部的姿势，因而能够以更单纯容易的方法实现标记部的准确跟踪。

另一方面，如上所述的光学跟踪系统1000在所述标记部1110的姿势的基础上，可以决定所述标记部1110的位置。

下面以附图为参照，更详细地说明决定所述标记部1110位置所需的系统建模过程及据此决定所述标记部1110位置的过程。

图15是概略性地显示图10的光学跟踪系统的处理部为了决定标记部的位置所需的解题过程的流程图。

如果参照图15，首先，针对具有上述构成的所述光学跟踪系统1000执行系统建模(S2100)。

所述系统建模为了获得所述标记部1110(参照图10)的位置，不同于前面说明的坐标变换式，包括与所述标记部1110的第1透镜1114(参照图10)中心的坐标对应的所述第2坐标(与所述第6坐标相同)地执行。

接着，从所述系统建模的结果校准位置变换矩阵[T](S2200)。

所述位置变换矩阵[T]由于所述第1成像部1120a(参照图10)与所述第2成像部1120b(参照图10)隔开，意味着把所述第1成像部1120a的位置变换成所述第2成像部1120b的位置的矩阵。

接着，获得所述标记部1110的位置(S2300)。

具体而言，获得所述标记部1110的所述第1透镜1114中心的三维坐标。

图16是用于说明在图15的解题过程中执行系统建模的过程的概念图。

如果参照图16，针对与所述标记部1110的第1透镜1114中心坐标对应的所述第2坐标(P2)及与所述第1成像部1120a的所述图案1112的第1图像上的第1像素坐标相应的所述第4坐标(P4)之间，设置第3坐标变换式。所述第3坐标变换式可以如下述数学式23所示表现为矩阵方程式。

(数学式23)

其中，(u’,v’)为所述第4坐标(P4)，(X,Y,Z)为所述第2坐标(P2)，[A_L]为所述第2变换矩阵，[I]为3x3形态的恒等矩阵(identity matrix)，[0]为3x1形态的零矩阵。如图16所示，所述第1成像部1120a的第2透镜1122a)为原点，因此，以此为基准，就所述第4坐标(P4)而言，旋转变换部分显示为恒等矩阵，而且，位置变换部分显示为零矩阵，可以如[I|0]所示表现。

接着，针对与所述标记部1110的第1透镜1114中心坐标对应的所述第6坐标(P6)(与所述第2坐标(P2)相同)及与所述第2成像部1120b的所述图案1112的第2图像上的第2像素坐标相应的所述第8坐标(P8)之间，设置第4坐标变换式。当设置所述第4坐标变换式时，包括所述第1成像部1120a及所述第2成像部1120b之间的位置变换矩阵[T]地进行设置。因此，所述第4坐标变换式可以如下述数学式24所示表现为矩阵方程式。

(数学式24)

其中，(u'₂,v'₂)意味着所述第8坐标(P8)，(X,Y,Z)意味着第6坐标(P6)(与所述第2坐标(P2)相同)，A_R意味着所述第4变换矩阵，[R_LR]具有3x3形态，意味着定义图11等中说明的所述第1成像部1120a相对于所述第2成像部1120b的姿势的矩阵，[T]具有3x1形态，意味着把所述第1成像部1120a的位置变换成所述第2成像部1120b的位置的位置变换矩阵。如图16所示，所述第1成像部1120a的第1透镜1122a)为原点，因此，以此为基准，就所述第2成像部1120b的所述第8坐标(P8)而言，旋转变换部分用矩阵[R_LR]代表，位置变换部分用[T]代表，可以如[R_LR|T]所示表现。

所述系统建模中出现的因子除位置变换矩阵[T]之外，均是从前面图11至图14中获得的因子。因此，如果获得位置变换矩阵[T]，则可以获得所述第2坐标(P2)(与所述第6坐标(P6)相同)，即，获得所述标记部1110的位置。

下面以附图为参照，更详细地说明作为所述系统建模的结果而获得的第3及第4坐标变换式中校准所述位置变换矩阵[T]的过程(S2200)。

图17是显示在图15的解题过程中校准位置变换矩阵的过程的流程图。

如果参照图17，首先，获得所述第1及第2成像单元1124a、1124b分别拍摄的第1中心坐标及第2中心坐标(S2210)。

其中，所述第1及第2中心坐标分别意味着所述第1及第2成像单元1124a、1124b在拍摄所述图案1112时显示的视野范围(filed of view)的中心，可以获得多个中心坐标。

然后，利用获得的所述第1及第2中心坐标，算出基础矩阵(fundamental matrix)[F](S2220)。

所述基础矩阵可以如数学式25所示表现。

(数学式25)

在数学式25中，下标字j代表获得多个中心坐标时获得的多个数据的序号。

如果把数学式25整理成所述基础矩阵[F]的成分，则可以获得数学式26，如果以数学式26为例，针对至少8个点，作为一个示例而应用诸如奇异值分解(SVD)的方法，可以获得所述基础矩阵[F]。

(数学式26)

接着，利用获得的基础矩阵[F]，算出本质矩阵(essential matrix)[E](S2230)。

所述本质矩阵[E]如数学式27所示表现。

(数学式27)

从数学式27算出的本质矩阵[E]表现为位置变换及旋转变换之积，因此，如果如数学式28所示进行整理，则可以求出对应于位置变换成分的矩阵[t]_X。

(数学式28)

E＝[t]_xR_LR

所述矩阵[t]_X可以与所述位置变换矩阵相同，但必要时，可以乘以换算系数(scale factor)而算出位置变换矩阵。

因此，接下来获得换算系数(S2240)。

所述换算系数可以通过在至少2个位置测量标记而获得。例如，可以通过使标记移动配置于已知隔开距离的至少2个标记位置进行测量而算出。

接着，利用获得的所述本质矩阵[E]和所述换算系数，获得位置变换矩阵[T](S2250)。

具体而言，所述位置变换矩阵[T]可以把以获得的所述矩阵[t]_X成分中的t_x、t_y、t_z为成分的3x1形态的矩阵(t_x,t_y,t_z)^T乘以换算系数而算出。

下面以附图为参照，更详细地说明利用所述校准的位置变换矩阵[T]而获得所述标记部1110的位置的过程(S2300)。

图18是显示在图15的解题过程中获得标记部的位置的过程的一个示例的流程图。

如果参照图18，首先，从对于所述第1成像单元1120a的第1位置变换式，获得第1方程式(S2310)。

具体而言，如数学式29所示定义作为所述第1位置变换式的数学式23。

(数学式29)

如果在数学式29的两边对自己自身进行外积，放入0，对其整理，则可获得对应于所述第1方程式的数学式30。

(数学式30)

接着，从对于所述第2成像单元1120b的第2位置变换式，获得第2方程式(S2320)。

具体而言，如数学式31所示定义作为所述第2位置变换式的数学式24。

(数学式31)

如果对数学式31应用与获得所述第1方程式的过程(S2310)相同的过程，则可以获得所述第2方程式。

对应于所述第1方程式的数学式30包括2个方程式，以相同的方式，所述第2方程式也包括2个方程式，因而对应于两个成像单元，共可获得4个方程式。

然后，从所述第1及第2方程式和位置变换矩阵[T]获得所述标记部1110的位置(S2330)。

具体而言，把校准的所述位置变换矩阵[T]应用于所述第1及第2方程式，可以获得所述标记部1110的所述第1透镜1114中心的三维坐标。

图19是显示在图15的解题过程中获得标记部的位置的过程的另一示例的流程图。

如果参照图19，首先从对于所述第1成像单元1120a的第1图案坐标变换式，获得第3方程式(S2350)。

具体而言，如数学式32所示设置并整理对所述第1位置变换式进行变形的第1图案坐标变换式。

(数学式32)

如果把数学式32整理成方程式，则可以获得数学式33。

(数学式33)

(m_{i_31}u′-m_{i_11})(u-u_c)r₁₁+(m_{i_31}u′-m_{i_11})(v-v_c)r₁₂+(m_{i_31}u′-m_{i_11})f_br₁₃+(m_i_₃₁u′-m_{i_11})X+(m_{i_32}u′-m_{i_12})(u-u_c)r₂₁+(m_{i_32}u′-m_{i_12})(v-v_c)r₂₂+(m_{i_32}u′-m_{i_12})f_br₂₃+(m_{i_32}u′-m_{i_12})Y+(m_{i_33}u′-m_{i_13})(u-u_c)r₃₁+(m_{i_33}u′-m_{i_13})(v-v_c)r₃₂+(m_{i_33}u′-m_{i_13})f_br₃₃+(m_{i_33}u′-m_{i_13})Z+(m_{i_34}u′-m_{i_14})＝0

(m_{i_31}v′-m_{i_21})(u-u_c)r₁₁+(m_{i_31}v′-m_{i_21})(v-v_c)r₁₂+(m_{i_31}v′-m_{i_21})f_br₁₃+(m_{i_31}v′-m_{i_21})X+(m_{i_32}v′-m_{i_22})(u-u_c)r₂₁+(m_{i_32}v′-m_{i_22})(v-v_c)r₂₂+(m_{i_32}v′-m_{i_22})f_br₂₃+(m_{i_32}v′-m_{i_22})Y+(m_{i_33}v′-m_{i_23})(u-u_c)r₃₁+(m_{i_33}v′-m_{i_23})(v-v_c)r₃₂+(m_{i_33}v′-m_{i_23})f_br₃₃+(m_{i_33}v′-m_{i_23})Z+(m_{i_34}v′-m_{i_24})＝0

接着，从对于所述第2成像单元1120b的第2图案坐标变换式，获得第4方程式(S2360)。

本步骤除对象不是所述第1成像单元1120a而是所述第2成像单元1120b之外，实质上与获得所述第3方程式的步骤(S2350)相同。

对应于所述第3方程式的数学式33包括2个方程式，以相同的方式，所述第4方程式也包括2个方程式，因而对应于两个成像单元，共可获得4个方程式。

然后，从所述第3及第4方程式和位置变换矩阵[T]，获得所述标记部1110的位置(S2370)。

具体而言，把校准的所述位置变换矩阵[T]应用于所述第1及第2方程式，可以获得所述标记部1110的所述第1透镜1114中心的三维坐标。

下面以附图为参照，更详细地说明所述处理部1130算出所述标记部1110的位置的方法。

图20是显示本发明一个实施例的光学跟踪系统的标记部位置算出方法的流程图。

如果参照图20，首先，借助于所述第1及第2成像单元1124a,1124b的拍摄而获得多个坐标值(S2510)。

所述坐标值的获得实质上与图17中说明的获得所述第1中心坐标及所述第2中心坐标的过程(S2210)相同，作为一个示例，至少获得8个坐标值。

接着，获得换算系数(S2520)。

所述换算系数的获得实质上与图17中说明的步骤S2240相同。

然后，利用获得的坐标值和换算系数，校准位置变换矩阵(S2530)。

所述校准实质上与图15中说明的步骤S2200、图17中具体说明的步骤S2250的过程相同，因而所述处理部1130只利用校准所需的最终方程式，便能够校准所述位置变换矩阵。

接着，利用校准的位置变换矩阵，获得标记部1110的位置(S2540)。

所述标记部1110的位置的获得实质上与图15中说明的步骤S2300、图18中具体说明的步骤S2310至步骤S2330的过程或图19中具体说明的步骤S2350至步骤S2370的过程相同，所述处理部1130如所述过程中的步骤S2330或步骤S2370所示，可以只利用获得所述位置所需的最终方程式。

根据如上所述的光学跟踪系统，针对包括特定信息的图案并小型化的标记部，应用立体方式进行建模，从而能够更准确地决定所述标记部的位置，因而能够以更单纯容易的方法实现准确的标记部跟踪。

在前面说明的本发明的详细说明中，参照本发明的优选实施例进行了说明，但只要是相应技术领域的熟练从业者或相应技术领域的普通技术人员便会理解，在不超出后述专利权利要求书中记载的本发明的思想及技术领域的范围内，可以多样地修订及变更本发明。因此，前述的说明及下面的附图应解释为并非限定本发明的技术思想，而是对本发明的示例。

(附图标记说明)

100,1000：光学跟踪系统；110,1110：标记部

112,1112：图案； 114,1114：第1透镜

120,1120：成像部； 122,1122：第2透镜

124,1124：成像单元； 130,1130：处理部