针对多目标柔性作业车间调度问题的含救济算子的混合遗传算法的利记博彩app
本发明用于制订多目标柔性作业车间调度的生产调度计划。
背景技术:
柔性作业车间调度问题是传统作业车间调度问题的一般化。不同于传统作业车间调度问题中每个工序只能在唯一一台机器上加工的特点,柔性作业车间调度问题中的每个工序通常能够在多台机器上加工,问题因此变得更加复杂,是一个NP困难问题。而实际生产环境中通常又会有多个目标,将问题变得更加复杂。以遗传搜索和邻域搜索组合的混合遗传算法已经被广泛运用于这类问题的求解,这种组合使算法同时具备了全局搜索能力和局部搜索能力。然而,算法对每个得到的解的利用仍有待提高。
技术实现要素:
本算法是针对多目标柔性作业车间调度的混合遗传算法,通过对混合遗传算法的改进使算法对每个得到的解利用率大大提高。本算法对混合遗传算法的改进主要包括以下方面:
本算法对传统遗传局部搜索算法的改进主要包括以下方面:第一,多目标柔性作业车间调度方案的编码方式的复杂性;第二,可行的解(调度方案)在经过交叉、变异操作后可能产生不可行的解(调度方案);第三,局部搜索可能作用于局部最优解,会产生无意义的搜索过程;第四,搜索过的解可能被重复搜索;第五,以加权法解决多目标问题时各目标函数的加权值不易确定;第六,一个解的邻域解数量非常多,占用计算时间过多;第七,已经产生的优良解(调度方案)可能在之后的迭代过程中被遗失。
本发明解决其技术问题所采用的技术方案是:第一,采用一种新的编码方式;第二,采用一种专门用于本编码方式的交叉算子和突变算子;第三,采用一种通过各目标的相对重要性为各目标函数赋加权值;第四,对每个解同时进行遗传搜索和局部搜索;第五,在对每个解进行遗传搜索与局部搜索的同时,对劣解执行救济算子;第六,在局部搜索中,只随机选取每个当前解的部分邻域解进行检测;第七,设置精英组保存搜索过程中发现的非支配解。
本发明的有益效果:第一,简化了编码过程;第二,避免了可行的解(调度方案)经交叉和突变后出现不可行的解(调度方案);第三,使各目标函数加权值更加符合实际生产情况;第四,对每个得到的解的利用率提高;第五,救济算子使劣解也得到了充分的利用;第六,避免了局部搜索占用过多的计算时间;第七,避免了非支配解的遗失。
附图说明
下面结合附图和实施例对本发明型进一步说明。
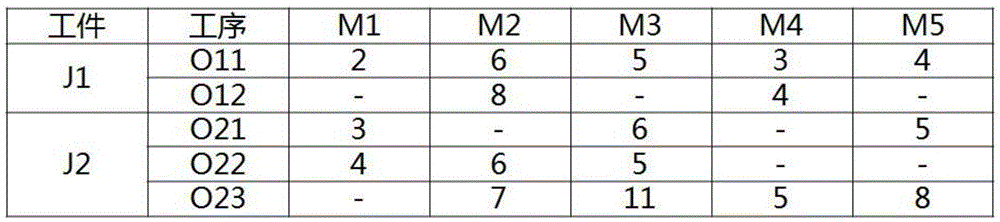
图1是柔性作业车间调度的示例图。
图2是编码结构的示意图。
图3是机器选择部分编码方式的示例图。
图4是工序序列部分编码方式的示例图。
图5是解码过程的示例图。
图6是非支配解的示意图。
图7是救济算子的示例图。
图8目标函数相对重要性的示例图。
图9是两点交叉算子示意图。
图10是基于工序编码交叉算子的示例图。
图11是机器选择部分编码的突变算子的示例图。
图12是工序序列部分编码的突变算子的示例图。
图13是含救济算子的混合遗传算法的流程的示意图
图14是算法详细流程的示意图。
具体实施方式
一、柔性作业车间调度问题
在传统的作业车间调度问题中,每个工序只能在唯一一台机器上加工。而对于柔性作业车间调度问题而言,每个工序能够在多台机器上加工,这从图1的示例中可以看出(图1中的“-”表示该机器无法加工此工序)。这种改变使问题模型更加符合实际的生产情境,但同时也加大了问题的复杂性。
二、生产信息的表示
1.n个工件:J1,J2,…,Jn。
2.m台机器:M1,M2,…,Mm。
3.工件Ji的第j道工序:Oij。
4.工序集W:将J1-Jn上的工序依次排列,
W={w1,w2,…},
(1)
“w”的下标为工序集中每个工序的编号,从1开始依次编号。
5.工件集中工序wi在第j台机器的加工时间:tij。
6.工序的机器集Mij:可加工工序Oij的机器的集合
Mij={m1,m2,…},
(2)
“m”的下标为机器集中每台机器的编号,从1开始依次编号。
7.全部工件的全部加工时间T:
每一行依次表示工序集(式(1))中的工序,每一列以此表示机器集(式(2))中的机器。如果工序i无法在机器j上加工,则tij=-1。
三、编码方式
如图2所示的编码结构,本编码方式对每个解的编码分为两个部分,分别为机器选择部分和工序序列部分。
1.机器选择部分的编码
如图3所示的编码示例(生产信息对应图1),编码的每一位依次对应工序集(式(1))上的工序,编码的每一位的值为加工该工序的机器在机器集(式(2))中的编号。
2.工序序列部分的编码
如图4所示的编码示例(生产信息对应图1),每个工件的每个工序都用此工件的编号表示,以同一编码值出现的顺序依次表示每个工件的各 工序,编码的顺序表示各工序的加工顺序。
3.解码过程
如图5所示的解码示例(生产信息对应图1),首先将工序序列部分的工序依次在机器选组部分找到加工机器,然后将这些工序依次加入对应机器,即可得到生产调度方案。
四、非支配解
对于最大化n个目标函数f1(x),f2(x),…,fn(x),当两个解x、y满足:
则称解y支配解x。
如果一个解不被多目标优化问题的任何其他解支配,那么这个解被称为一个非支配解。
对于两目标优化问题(最大化目标函数)的非支配解可以被图6形象地描述出来。
五、精英组
通过将每一代中的非支配解加入精英组,并在每一代更新精英组(即删掉加入新的解后精英组中不再是非支配解的解)。
六、救济算子
救济算子是一种优化劣解的算子。
救济空间用来存储种群中的优良个体的共有序列。
如图7所示的示例(生产信息对应图1),救济算子的执行过程如下:
1.选择工件
随机选择一个工件。
2.确定救济空间
对于机器选择部分,从最优解将被选择工件的工序所使用的加工机器编号提取;对于工序序列部分,从最优解中将被选择工件的工序的位置提取。将提取到的信息记入救济空间。
3.优化劣解
对于劣解的机器选择部分,将被选择工件的工序所使用的加工机器的编号更换为救济空间中的机器编号;对于劣解的工序序列部分,将被选择工件的工序先加入对应位置,再将其他工件的工序按照原有的相对位置加入供需序列部分的空位。
七、通过相对重要性的权值确定法
实际生产中,各目标函数间的相对重要性通常由生产者根据实际情况得出。加权法解决多目标(f1(x),f2(x),…,fn(x))问题时,适应度函数为
f(x)=w1f1(x)+w2f2(x)+…+wnfn(x), (6)
其中
wi≥0,i=1,2,…,n, (7)
w1+w2+…+wn=1. (8)
以如图8所示的三个目标函数的相对重要性示例为例,加权值的确定方法
如下:
1.将相对重要性表(图8)转化为矩阵:
2.对得到的矩阵的各列进行标准化(即对每列分别乘以一个数,使各列的和为1):
3.对各列标准化后的矩阵的各行进行标准化(即先将每行求和,再对每行分别乘以一个数,使各行的和为1):
4.对行标准化后的矩阵的每行依次表示三个目标函数的加权值,即f1、f2、f3的加权值分别为w1=0.578、w2=0.302、w3=0.120。
八、两点交叉算子
在本算法中,两点交叉算子被用于编码机器选择部分的交叉。
如图9所示,两点交叉算子的步骤为:
1.随机选择编码中两个不同的位置。
2.交换两个位置点之间的部分。
九、基于工序编码交叉算子
在本算法中,基于工序编码交叉算子被用于编码的工序序列部分的交叉。
如图10的示例所示,基于工序编码交叉算子的步骤为:
1.随机地从工件中产生两个子工件集Js1和Js2。
2.把父代1中属于Js1的元素复制入子代1中的相同位置,把父代2中属于Js2的元素复制入子代2中的相同位置。
3.把父代2中除Js2所含元素以外的其他元素按顺序填入子代1的空位置,把父代1中除Js1所含元素以外的其他元素按顺序填入子代2的空位置。
十、机器选择部分的突变算子
如图11的示例所示,机器选择部分的突变算子为:
1.在机器选择部分随机选择一个位置。
2.从该位置对应工序的机器集中随机选择一台机器(的编号)替换当前机器(的编号)。
十一、工序序列部分的突变算子
如图12的示例所示,工序序列部分的突变算子为:
1.在工序序列部分随机选择两个位置。
2.交换这两个位置对应的值(工序)。
十二、只检测部分邻域解的局部搜索算法
预先指定邻域解检测个数k。
那么,对于当前解的局部搜索过程如下:
1.随机选择当前解的一个邻域解。
2.如果此邻域解比当前解更优,则邻域解作为新的当前解替换原来的当前解,并返回本步骤1;否则执行下一步。
3.如果已经检测了当前解的k个邻域解,即当前解被检测的k个邻域解中没有更优的解,则程序结束;否则返回本步骤1。
十三、轮盘赌选择法
预先制定要选择的解的个数为n。
轮盘赌选择法的过程如下:
1.计算每个个体(xi)被遗传到下一代的概率P(xi):
其中N为待选择种群的种群规模。
2.计算每个个体(xi)的积累概率qi:
3.在[0,1]之间产生一个随机数r。
4.如果r<q1,则个体x1被选择;如果qk-1<r≤qk,则选择个体xk。
5.对本步骤3、步骤4重复n次。
十四、含救济算子的混合遗传算法
如图13,假设种群规模为Npop,含救济算子的混合遗传算法的执行步骤为:
1.更新救济空间,即随机选择一个工件,在救济空间中记录最优解中与该工件有关的信息。
2.随机选择Npop/2个个体,进行遗传搜索(交叉、突变)。
3.(与2同时进行)随机选择Npop/2个个体,进行遗传搜索(交叉、突变)。
4.(与2同时进行)选择适应度最差的Npop/2个个体,执行救济算子。
5.将通过本步骤2、步骤3、步骤4产生的解合并,从中选择Npop个解进入下一代。
十五、算法详细流程如下
如图14。
设种群规模为Npop;突变概率为Pm;局部搜索中对每个当前解检测k个邻域解;算法迭代的终止条件为已经迭代了n次。
步骤一—初始化种群
1.根据生产信息分别产生全部工件的工序集W(式(1))和全部工序的机器集Mij(式(2))。
2.按照工序集中工序的顺序,依次从相应工序的机器集中随机选择一台机器,以机器集中的编号组成机器选择部分的编码。
3.根据每个工件的工序数产生相应个数的数值为工件编号的数,并将这些数随机排列组成工序序列部分的编码。
4.机器选择部分的编码在前,工序序列部分的编码在后,将它们组合。
5.返回本步骤2,直至已经产生Npop个解。
步骤二—更新精英组
1.将当前种群中的非支配解复制入精英组。
2.检测精英组中的解,将被其他解所支配的解从精英组中删除。
步骤三——更新救济空间
1.选择工件
随机选择一个工件。
2.确定救济空间
对于机器选择部分,从最优解将被选择工件的工序所使用的加工机器编号提取;对于工序序列部分,从最优解中将被选择工件的工序的位置提取。将提取到的信息记入救济空间。
步骤四—计算适应度函数值
1.根据生产者给出的相对重要性关系,通过式(9)、式(10)、式(11)确定各目标函数的加权值。
2.通过式(6)计算每个解的适应度函数值。
步骤五——遗传搜索
1.随机选择Npop/2个个体。
2.交叉
随机将被选择的解两两一组作为一对父代解。
对每个解的机器选择部分使用如图9所示的两点交叉算子进行交叉,对每个解的工序序列部分采用如图10所示的基于工序编码交叉算子进行交叉。
3.根据突变概率Pm计算进行交叉的解的数目,并随机选出相应数目的解。对每个解的机器选择部分和工序序列部分分别采用如图11所示的突变算子和如图12所示的突变算子进行突变。
步骤六—局部搜索(与步骤五同时进行)
(对每个解)
1.随机选择当前解的一个邻域解,邻域解通过遗传搜索中的突变算子产生。
2.如果邻域解优于当前解,则以邻域解作为当前解替换原当前解,返回本步骤1;否则,执行下一步。
3.如果已经检测了当前解的k个邻域解,则局部搜索结束,当前解即为局部搜索的结果;否则,返回本步骤1。
步骤七——救济算子(与步骤五同时进行)
1.获取步骤三得到的救济空间中的信息,包括被选择的工件及其加工机器和工序位置。
2.选择适应度最差的Npop/2个个体。
3.对于劣解的机器选择部分,将被选择工件的工序所使用的加工机器的编号更换为救济空间中的机器编号;对于劣解的工序序列部分,将被选择工件的工序先加入对应位置,再将其他工件的工序按照原有的相对位置加入供需序列部分的空位。
步骤七—选择
采用轮盘赌选择法选择:
1.通过式(12)计算每个个体(xi)被遗传到下一代的概率P(xi)。
2.通过式(13)计算每个个体(xi)的积累概率qi。
3.在[0,1]之间产生一个随机数r。
4.如果r<q1,则个体x1被选择;如果qk-1<r≤qk,则选择个体xk。
5.对3、4重复Npop次,以选择到Npop个个体。
步骤八—迭代
1.如果算法已经迭代了指定次数,则执行下一步骤(更新精英组);否则,返回步骤二。
步骤十一—更新精英组
1.将当前种群中的非支配解复制入精英组。
2.检测精英组中的解,将被其他解所支配的解从精英组中删除。
- 还没有人留言评论。精彩留言会获得点赞!