针对多目标流水车间调度的加权式遗传局部搜索算法的利记博彩app

本发明型专利用于制订多目标流水车间调度的生产调度计划。

背景技术：

遗传算法是一种高效的全局搜索算法，其与局部搜索算法的结合，即遗传局部搜索算法，使得算法对于非支配解的搜索能力大大提高。目前，这种全局搜索与局部搜索相结合的算法已经被广泛地运用于生产优化之中，并取得了很好的效果。然而，现有的局部搜索算法往往难以简单高效地找到多目标问题的全部非支配解。

技术实现要素：

本算法针对传统的遗传局部搜索算法作出改进，以简单高效地找到多目标流水车间调度问题的全部非支配解。本算法对传统遗传局部搜索在以下三个方面进行改进：第一，每个目标函数的加权值不易确定；第二，对局部搜索过程中产生的大量邻域解的比较往往占据大量的计算时间；第三，局部搜索方向不够全面；第四，搜索过程中得到的优良解可能在之后的算法迭代过程中被遗失。

本发明型解决其技术问题所采用的技术方案是：第一，通过随机加权法为每个目标函数赋予加权值；第二，限制局部搜索过程中对每个当前解搜索的邻域解的个数；第三，以产生子代解的父代解所使用的加权值作为子代解在局部搜索中的目标函数加权值；第四，采用精英策略，将每一代中的非支配解存入暂时组并逐代更新。

本发明型的有益效果：第一，使确定目标函数加权值的过程不再困难；第二，平衡了全局搜索与局部搜索；第三，局部搜索中的每个解都有自己独特的搜索方向，使得局部搜索的方向多样化；第四，避免了产生的优良解在之后算法的迭代过程中被遗失。

附图说明

下面结合附图和实施例对本发明型进一步说明。

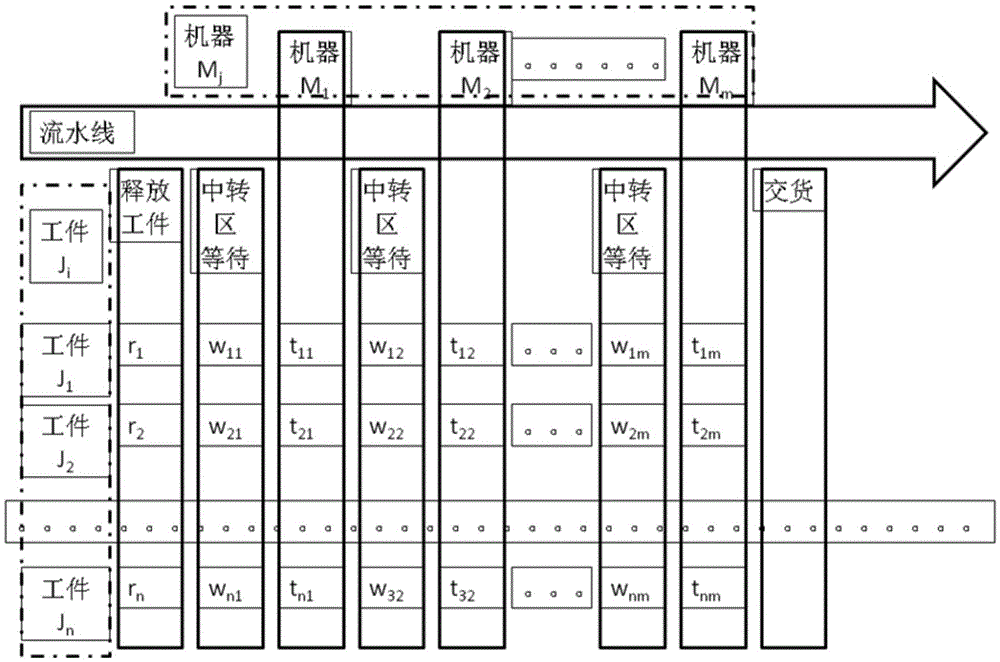
图1是流水车间调度的示意图。

图2是局部搜索方向的示意图。

图3是非支配解的示意图。

图4是精英策略的示意图。

图5是加权式遗传局部搜索流程的示意图。

图6是两点交叉算子示意图。

图7是移动突变示意图。

图8是算法详细流程的示意图

具体实施方式

一、生产信息的表示

如图1，设在流水车间中，有n个待生产的工件J₁，J₂，…，J_n，有m台机器M₁，M₂，…，M_m，工件J_i的释放时间为r_i，工件J_i的在机器M_j前的等待时间为w_ij，工件J_i的交货时间：d_i。

二、调度方案的表示方法：

机器i上的调度方案表示为X_i＝(s₁，s₂，…，s_n)，1≤i≤m(s_i表示工件编号，1≤i≤n)，则总调度方案表示为X＝(X₁，X₂，…，X_m)

三、随机加权法

对n个目标的加权值的赋值方法：

1.随机产生n个和为1的加权值random₁，random₂，…，random_n；

2.第i个目标函数的加权值w_i为

w_i＝random_i/(random₁+…random_n)，i＝1，2，…，n.

四、只检测部分邻域解的局部搜索算法

指定邻域解检测个数k，将产生当前解X的父代解的目标函数加权值作为当前解X的目标函数加权值(这将使每个当前解都有自己独特的局部搜索方向，从而使局部搜索方向多样化，其特点被图2形象地描述出来)，局部搜索采用移动突变的方式产生邻域解。

那么，对于解X的局部搜索过程如下：

1.检测当前解X的一个邻域解X’；

2.如果X’是比X更优的解，则用X’替代当前解X并返回1；否则执行下一步；

3.如果当前解X的随机选择的k个邻域解已经被检测，即X的被检测的k个邻域解中没有更优的解，则程序结束；否则返回1。

五、非支配解

对于最大化n个目标函数f₁(x)，f₂(x)，…，f_n(x)，当两个解x、y满

足

且

f_j(x)<f_j(y)时，则称解y支配解x。如果一个解不被多目标优化问题的任何其他解支配，那个解被称为一个非支配解。对于两目标优化问题(最大化目标函数)的非支配解可以被图3形象地描述出来。

六、精英策略

如图4，本算法的执行过程中含有两组解，分别为当前种群和存储非支配解的暂时组。

每一代种群首先用本种群中的非支配解更新暂时组，并随机选择指定个数的解；然后，该种群经遗传算子处理后，将之前随机选择的非支配解加入当前种群，共同进行局部搜索；局部搜索结束后产生的种群作为下一代继续执行上述过程。七、加权式遗传局部搜索

如图5，本算法在初始化种群后，首先确定目标函数加权值，接着通过遗传算子对种群进行全局搜索，然后进行局部搜索，而后采用精英策略保护非支配解，最后通过对上述过程的反复迭代来寻找全部的非支配解。

八、两点交叉算子

如图6

九、移动突变

如图7

十、算法详细流程如下

如图8

步骤一——初始化(产生初始解)

1.产生m个序列(m为机器数)，每个序列为数1-n的一个随机排序序列(n为待生产工件数)。

2.根据种群规模N_pop，产生对应数目的初始解。

步骤二——计算目标函数值

1.计算目标函数f₁(x)，f₂(x)，…，f_n(x)的值。

步骤三——更新暂时组的非支配解

1.寻找初始种群中的非支配解。

2.将初始解中的非支配解复制入暂时组。

步骤四——计算适应度函数值

对每个解——

1.确定加权值

w_i＝random_i/(random₁+…random_n)，i＝1，2，…，n.

2.计算适应度函数值：

f(x)＝w₁f₁(x)+w₂f₂(x)+…+w_nf_n(x).

步骤五——选择优良个体

1.计算每个个体(解)的选择概率

其中Ψ表示当前种群，f(x)为解x的适应度值，f_min(Ψ)＝min{f(x)|x∈Ψ}。

2.根据选择概率，选择选择概率大的(N_pop-N_elite)个个体(解)。

步骤六——交叉

1.根据交叉概率计算进行交叉的解的数目，随即选出相应个数的解。

2.随机将被选择的个体两两一组作为一对父代解，运用两点交叉算子进行交叉。对每对父代解交叉时，分别对两个解的每行进行交叉，再把结果重新组合成子代解。

步骤七——突变

1.根据突变概率计算进行交叉的解的数目，随即选出相应个数的解。

2.对被选择的个体进行移动突变。对每对父代解进行突变时，分别对每行突变，再把结果重新组合成子代解。

步骤八——局部搜索

1.从暂时组(步骤三产生)中随机选择N_elite个解，加入有(N_pop-N_elite)个解的当前种群，构造一个有N_pop个解的种群。

2.(对每个解)通过移动突变随机产生k个邻域解。

3.(对每个解)通过选择该解的父代解的适应度函数加权值来构造该解的适应度函数，然后计算这k个邻域解的适应度函数值。

4.(对每个解)如果这k个邻域解中有比该解更优的解，则以之替换该解；否则，该解不做变化。

步骤九——迭代

1.如果算法已经搜索指定个数的解，则算法结束；否则返回步骤二。

步骤十——产生调度方案

1.迭代结束后，当前种群中的最优解和暂时组中的解即为算法所求得的优良解，根据调度方案的表示方式，即可将这些解转换为对应的调度方案。