恒定阻抗的变步长元件伴随模型的利记博彩app
本发明涉及一种在步长改变时具有恒定阻抗的元件伴随模型,可以用于仿真计算中的事件处理和数值震荡抑制,属于电力系统电磁暂态仿真以及计算机辅助电路分析技术等领域。
背景技术:
在电磁暂态仿真程序中,为了仿真电力电子设备等非线性元件,通常可以使用理想开关或分段线性化非线性电阻模拟;电磁暂态仿真程序需要有效地处理这些电力电子设备元件的状态改变所导致的事件。传统的电磁暂态仿真程序采用定步长仿真,而电力电子器件的动作时刻却可能落在仿真步之间,而对于电力电子器件的动作时刻的精确模拟很多情况下却是必要的。采用变步长可以方便地在电力电子器件的动作时刻插入仿真点,为了获得较好的数值稳定性,电磁暂态仿真程序通常会使用隐式的数值方法(常用梯形法),改变仿真步长会导致元件的伴随模型的导纳发生变化,这就需要重新形成系统方程的导纳阵,并重新进行LU分解,降低仿真的效率。为了解决这个问题,目前主流的电磁暂态仿真程序都是通过插值的方法在步长间插入仿真点:电磁暂态仿真程序依然使用固定的步长仿真,但是当发现某个器件在步长之间发生了事件时,通过线性插值得到事件发生时刻系统的状态。
电磁暂态仿真程序通常会采用梯形法,梯形法虽然是A稳定的,但是却不是L稳定的;当系统中有快速的暂态过程的时候,如果仿真步长相对于暂态过程太大,非状态变量会产生围绕准确解来回震荡的现象。目前解决电磁暂态仿真程序数值震荡问题主要有两种方法:文献“Neville Watson and Jos Arrillaga,“Power System Electromagnetic Transients Simulation”Published by Institute of Engineering and Technology,London,United Kingdom,2003.”的NOS方法(Numerical Oscillation Suppression)以及文献“Marti,Jose R.;Lin,Jiming,"Suppression of numerical oscillations in the EMTP,"in Power Systems,IEEE Transactions on,vol.4,no.2,pp.739-747,May 1989.”中的CDA方法(Critical Damping Adjustment)。NOS的原理简单直观,既然变量是围绕准确的值来回震荡,那么相邻的两个计算点的中间位置必然很接近准 确值,因此NOS使用半个步长的插值来抑制数值震荡。由于为了准确模拟事件发生时刻,各元件已经实现插值功能,因此通过半步长插值抑制数值震荡,比较容易实现,电磁暂态仿真程序PSCAD/EMTDC就是使用的这种方式。CDA使用半步长的后退欧拉法抑制数值震荡,由于后退欧拉法是L稳定的方法,它可以有效地抑制由于快暂态过程造成的数值震荡,而且使用半步长的后退欧拉法所得到的诺顿等值的导纳与整步长的梯形法所得到的诺顿等值的导纳是一样的,这样可以避免修改和重新分解导纳矩阵,有些电磁暂态软件(如:EMTP-RV)就是使用的这类方法。
本发明针对电磁暂态仿真程序中元件模型可以表示为诺顿等值或戴维南等值的形式,对诺顿等值或戴维南等值中的电压和电流进行线性插值,从而得到具有恒定阻抗或导纳的元件伴随模型,避免了系统的导纳矩阵在捕捉准确事件时刻和抑制数值震荡时的变化,大大提高了计算效率;同时由于新得到的元件模型跟原有元件模型具有同样的结构形式,其实现不需要对程序已有结构进行调整,易于实现。
技术实现要素:
本发明提出一种变步长时具有恒定阻抗或导纳的元件伴随模型,避免系统导纳矩阵的重新形成和分解,大大提高了计算效率。该方法物理概念清晰,实现方式简单,对于电磁暂态仿真和计算机辅助电路分析软件开发有一定的意义。本发明的技术方案如下:
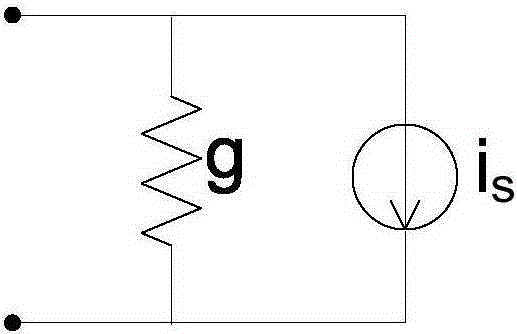
由于诺顿等值和戴维南等值的等价性,为了便于叙述,假定元件伴随模型均采用诺顿等值,当元件采用戴维南等值描述时,结果是类似的。在电磁暂态仿真程序或计算机辅助电路分析程序中,元件的伴随模型最终可以表示为如图1和(1)式所示的诺顿等值形式。
i(t+Δt)=gu(t+Δt)+is(t) (1)
其中g为元件诺顿等值导纳,is(t)为元件的诺顿等值电流,它是根据系统当前已知的状态计算出来的。当(1)式被用来从t时刻计算t+Δt时刻系统的状态时,对于t时刻到t+Δt时刻间的任何时刻t′∈(t,t+Δt],假定
t′=t+kΔt,k∈(0,1] (2)
假定电流在t时刻到t+Δt时刻是线性变化的,则有:
进一步可得:
类似地,对于电压可得:
将(4)和(5)式代入(1),可得:
i(t′)=gu(t′)+kiS(t)+(1-k)[i(t)-gu(t)] (6)
其中新伴随模型的诺顿等值电流由(7)式给出
i′s(t)=kiS(t)+(1-k)[i(t)-gu(t)] (7)
考虑到:
ihist(t-Δt)=i(t)-gu(t) (8)
(6)式也可以表示为:
i(t′)=gu(t′)+kihist(t)+(1-k)ihist(t-Δt) (9)
通过假定电压和电流在t时刻到t+Δt时刻间线性变化,由已有的诺顿等值(可以是任何数值方法得到的诺顿等值),(6)或(9)式给出了一个由t时刻的系统状态计算t′时刻系统状态的一个新的诺顿等值,或者说(6)或(9)式给出了一种新的变步长仿真的方式。由于其形式与经典的电磁暂态仿真程序完全一样,因此其实现可以完全照搬已有程序的流程,而且由于新的诺顿等值的导纳跟原来的完全一样,避免了导纳矩阵的修改和重分解。
当式(1)中的原始伴随模型是使用梯形法获得,且(2)式中的系数k取1/2时,通过(6)或(9)式所得到的新伴随模型与使用半步长的后退欧拉方法得到的伴随模型是完全一致的,因此通过(6)或(9)式所得到的新伴随模型像后退欧拉方法一样具有抑制数值震荡的作用。
附图说明
图1诺顿等值电路结构图。
图2电感元件。
具体实施例
下面通过实施例对本发明做进一步的补充说明:
例如,对如图2所示的电感使用梯形法进行离散化,可以得到元件的伴随模型的参数为:
is(t)=gu(t)+i(t) (11)
使用(6)式或者(9)式可以得到新的伴随模型参数为:
导纳g没有变化,依然通过(10)式计算;而诺顿等值电流则可以通过(12)式来计算。
i′s(t)=i(t)+(2k-1)gu(t) (12)
当k取1/2时,可知新伴随模型正好与使用半步长的后退欧拉法直接离散化电感所得到的伴随模型是完全一致的。
- 还没有人留言评论。精彩留言会获得点赞!