一种基于遗传蚂蚁算法的无人机全局路径规划方法与流程
本发明主要涉及无人自主水下航行器(auv)智能算法技术领域,具体涉及一种基于遗传蚂蚁算法的auv路径规划方法。
背景技术:
无人自主水下航行器(autonomousunderwatervehicle,auv)是水下机器人的一种,依靠自身的自治能力和控制自己以完成所赋予的使命。当前海洋及海洋科学的战略地位急剧上升,具有全球变化和走向深海两大发展趋势,逐渐形成从近岸向远洋、从浅水向深海拓展的新格局。auv目标小、水下隐蔽性较强,在详细海洋勘测、预警搜索侦察、反潜、反水雷、防御、战斗支援等方面均有不可估量的潜在应用价值。路径规划是保障auv航行安全必不可少的重要功能,它指综合考虑地形、威胁等多种因素,找到从起始点到目标点的最优航迹。
根据环境中障碍物的分类,可将auv的路径规划分为全局路径和局部路径两种规划,其中,全局路径规划主要针对仅包含静止、信息已知的障碍物对象的环境。
全局路径规划可分为两个步骤:环境建模与规划算法。环境建模从某种意义上说是路径规划的基础,合理的环境表示能有利于规划中搜索量的减少,才能有利于时空开销的减少,环境建模的方法直接影响路径规划的效率和准确性。
栅格法的原理是将整个空间用规划的小格点划分成许多小空间,非障碍物占据的栅格成为自由栅格,一般用白格表示,障碍物占据的栅格为非自由栅格,一般用黑格表示。路径规划的过程即为搜索自由栅格(白格)的最短路径的过程。该方法的特点是简单,易于实现,并易于扩展到三维环境;它的缺点是表示效率不高,存在着时空开销与求解精度之间的矛盾,当环境区域太大时,将使栅格的数量急剧增加,使搜索存在组合爆炸的问题。
现有研究对栅格法存在的缺陷进行了一定的改进,如李向军,霍艳丽等人提出了子平面分隔,即在一条轴上按照固定的间隔划分区间的方法,路径由每个平面上的一个点组成,将每一点的信息表示从三维降为二维,可有效简化数据的表示,同时减少了搜索栅格的数量。
基于生物智能的路径规划算法不必建立复杂的环境模型,目前应用较多的主要有遗传算法、蚁群算法等。这类算法的突出优点是可以方便的处理复杂问题模型和约束条件。
遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法。遗传算法模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选种群,并按某种指标从种群中选取较优的个体,利用遗传算子对这些个体进行组合,产生新一代的候选种群,重复此过程直到满足收敛目标。与一般的启发式优化搜索算法相比,群体搜索使遗传算法突破领域搜索的限制,可实现整个解空间上的分布式信息采集和探索,而遗传算子仅仅利用适应值度量作为运算指标进行随机操作,降低了一般启发式算法在搜索中对人机交互的依赖。遗传算法的缺点是对于系统中的反馈信息利用不够,当求解到一定范围时往往做大量无为的冗余迭代,求解精度效率低。选择保留精英算法(elitistgeneticalgorithm,ega)是遗传算法的一种,其基本思想在每次迭代中保留适应值最优的个体,该算法一定程度上提高了搜索效率,但仍存在着在算法后期搜索效率降低的问题。
蚂蚁算法真实地模拟了自然界蚂蚁群体的觅食行为。将蚂蚁算法应用于解决优化问题的基本思路为:用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多,随着时间的推进,较短的路径上累积的信息素浓度逐渐增高,选择该路径的蚂蚁个数也越来越多。最终,整个蚂蚁会在正反馈的作用下集中到较优的路径上。蚂蚁算法的缺点是初期信息素匮乏,求解速度慢。最大最小蚂蚁系统(max-minantsystem,mmas)对基本的蚂蚁算法从信息素更新、信息素浓度范围等方面进行了一定改进,提高了算法的收敛速度,但仍存在着搜索效率不高,搜索到最优解时间过长的问题。
遗传算法与蚂蚁算法的融合(geneticalgorithm-antalgorithm,gaaa),其基本思想是汲取两种算法的优点,克服各自的缺陷,优势互补。其基本思想是算法前过程采用遗传算法,充分利用遗传算法的快速性、随机性、全局收敛性,其结果是产生有关问题的初始信息素分布;算法后过程采用蚂蚁算法,在有一定初始信息素分布的情况下,充分利用蚂蚁算法并行性、正反馈性、求精解效率高等特点。两种基本算法的融合在一定程度上提高了算法的搜索速度,但仍存在融合机制没有充分利用两种算法的收敛特点和算法后期寻找最优解的效率不足的缺点。
虽然现有技术通过对混合算法的融合方式和融合时刻等方面的改进,提高了gaaa算法由于自身局限性而导致的收敛速度慢的问题,但在应用中仍然存在许多不足。
如梁旭,刘鹏飞,黄明等人提出了一种新的动态蚂蚁遗传混合算法,其动态地控制调用时机,并改进了信息素的更新方法,同时引入迭代调整阈值控制算法后期的遗传操作和蚂蚁规模,在一定程度上加快了种群的进化速度,但在应用中仍然存在许多不足。
总体来看,现有的路径规划方法中,环境建模部分通过对传统栅格法的改进,在数据量的存储与运算速度方面已经有了较大改进;但混合算法存在没有充分利用路径规划的特点,融合策略有待进一步改进,最优解的搜索效率和搜索精度需进一步提高的问题。
因此希望有一种基于改进的遗传蚂蚁混合算法的auv路径规划方法可以进一步克服或至少减轻现有技术上的上述缺陷。
技术实现要素:
针对现有技术存在的问题,本发明提供了一种基于遗传蚂蚁算法的无人机全局路径规划方法,提高了搜索效率,缩短最优路径的规划时间,使auv成功躲避障碍物,快速到达目标点。
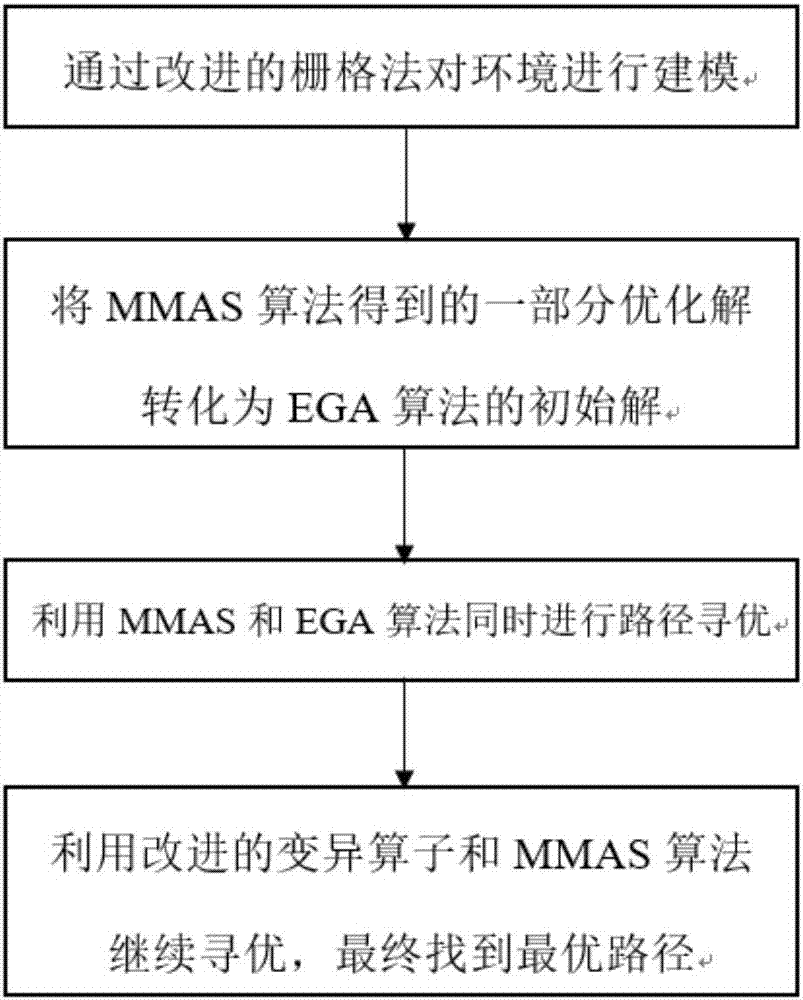
为解决上述技术问题,本发明采用了以下技术方案:一种基于遗传蚂蚁算法的无人机全局路径规划方法,包括以下步骤:
(1)通过改进的栅格法对环境进行建模;
(2)将mmas算法得到的部分优化解转化为ega算法的初始解;
(3)利用mmas和ega算法同时进行路径寻优;
(4)利用改进的变异算子和mmas算法继续寻优,最终找到最优路径
进一步的,步骤(1)中改进的栅格法对环境建模的步骤包括:
(1)环境处理:首先将auv简化为质点,将环境中障碍物长度等效为auv长度与自身原本长度之和,auv与障碍物最短安全距离定义为路径与障碍物边缘重合;然后使用栅格法对环境进行建模,将环境中的每一点用单元栅格表示,并对可行区域和障碍物区域做出不同划分;
(2)子区域划分:在三维环境下,以auv运动的主方向为x轴,将x轴坐标间距小于α的障碍物聚为一类,聚类结果记为n;接着在每一类障碍物中x轴最小值和最大值处作与x轴垂直的两个平面,从而划分成2n+1个子区间;二维环境依次类推。
进一步的,步骤(2)中mmas算法得到部分优化解转化为ega算法初始解的方法包括以下步骤:
a、对mmas和ega算法的参数进行初始化,所述参数包括蚂蚁数量m1,挥发系数ρ,种群数量m2,交叉概率pc,变异概率pm,最大迭代次数iter_max,信息素重要程度因子α,启发函数重要程度因子β,初始化时迭代次数iter设置为1;
b、确定解的表示形式,算法得到对路径的解用该路径经过的栅格信息集合标识;(采用区域划分的方法,可使解中的每一个栅格减少一个维度的信息,而按照步骤s12中子区域划分的方法,auv在不包含障碍物的子区间中的路径就可以只用起始和终点两个栅格表示,而在包含障碍物的子区间中再考虑用具体的栅格表示,减小了需要的栅格量,从而进一步减少了需处理和存储的数据量;)
c、通过迭代最优解和全局最优解的关系定义算法的转换时刻,将转化时刻mmas的路径解和此时全局最优解作为ega算法的初始解。
进一步的,步骤(3)中利用mmas和ega算法同时进行路径寻优时,
一方面,采用mmas算法继续优化解的质量,并以每次迭代得到的最优解更新路径信息素浓度,其计算公式如下:
式中,τij(t)表示t时刻ij两栅格间的信息素浓度,ρ表示挥发系数,
同时将ega算法每次迭代得到最优解用于信息素浓度的更新中。
每次迭代中,继续按照mmas算法,更新迭代最优解所对应路径上的信息素浓度;每次迭代中,执行ega算法的选择、交叉和变异操作,并将得到的解保留作为下一代ega算法的初始解群,循环次数iter=iter+1;变异算子包括两种,第一种变异算子为解在栅格序列中随机选取两个点,将这两个栅格位置对换形成新的解的序列,另一种变异算子为在解的栅格序列中随机选取两个点,将这两个栅格件的栅格按倒序排列形成新的栅格序列。
进一步的,步骤(4)中利用改进的变异算子和mmas算法继续寻优时,当算法陷入停滞状态时,算法中蚂蚁数量进行增加以提高找到粳稻路径的可能性;在ega算法中仅保留改进的变异算子。(此时最优解已接近理论上的全局最优解,仅保留对最优解的变异操作,且规定变异后的解得到了改进才得到保留;在每5次迭代中采用作用类似于2-opt优化的变异算子,有效改进解中交叉的路径)。
有益效果:相对于现有技术,本发明具有以下优点:1)采用新的子区域划分方法,简化了解的表达形式,减少了数据的计算量与存储量;2)设计了新的基本算法结合机制,根据mmas算法与ega算法的收敛速度的特点,采取了在每次中将迭代最优解和ega优化得到的最优解共同更新信息素的方法,提高了搜索最优解的效率;3)在算法陷入停滞状态时,采用了增大蚂蚁数量和改进的ega变异算子,进一步提高了最优路径的搜索效率。。
附图说明
图1为本发明所述auv路径规划方法的流程框图;
图2为本发明所述auv路径规划方法的算法逻辑流程图;
图3为本发明具体实施方式中25×25栅格环境下本发明的混合算法规划路径示意图;
图4为本发明具体实施方式中算法二在25×25栅格环境下的规划路径示意图;
图5为本发明具体实施方式中算法三在25×25栅格环境下的规划路径示意图;
图6为本发明在500×500×500栅格环境下三种算法比较的规划路径的示意图。
具体实施方式
下面结合附图并以具体实施例,进一步阐明本发明。应理解这些实施例仅用于说明本发明而不用于限制本发明的范围,在阅读了本发明之后,本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。
本发明的auv路径规划方法的工作原理:由于在大范围空间内,蚂蚁算法较遗传算法初始解质量明显改善,而mmas算法在仿真初期全局最优解会快速收敛,因而在算法初期采用mmas迅速改善解的质量;转入ega算法后,采用mmas与ega算法共同更新信息素的机制,可加快收敛速度的同时,保证信息素分布的多样性;在仿真后期陷入停滞状态时,采用变异算子和增加蚂蚁数量的mmas算法,保留优良解特征的同时,增加找到最优解的可能性。
在本发明一宽泛实施例中,路径规划方法包括以下步骤:
步骤s1,通过改进的栅格法对环境进行建模;
步骤s2,将mmas算法得到的一部分优化解转化为ega算法的初始解;
步骤s3,利用mmas和ega算法同时进行路径寻优;
步骤s4,利用改进的变异算子和mmas算法继续寻优,最终找到最优路径。
所述步骤s1中通过改进的栅格法对环境进行建模包括以下内容:
步骤s11,环境处理,将auv简化为质点,障碍物作适当“膨化”处理为球体(三维环境)或圆(二维环境),其半径为auv长度与自身长度之和,auv经过障碍物的最短安全距离定义为路径与障碍物球心(或圆心)的最短距离大于障碍物球体(或圆)半径,使用栅格法为环境建模,将环境中的每一点(包括障碍物)用单元栅格表示,进一步对可行区域和障碍物区域做出不同划分;
步骤s12,子区域划分,以三维环境为例,在auv运动的主方向x轴上,各点仅依据各障碍物的x坐标对障碍物进行聚类,将x轴坐标间距较小或x轴有重合的障碍物聚为一类,其聚类结果记为n;再在每一类中,以x坐标最小和最大处,作与x轴垂直、与yz平面平行的两个平面,则区域中共有2n个平面,划分为2n+1个子区间;二维环境依此类推。
所述步骤s2中将mmas算法得到的一部分优化解转化为ega算法的初始解包括以下内容:
步骤s21,初始化mmas和ega算法参数,主要包括设置蚂蚁数量m1,挥发系数ρ,种群数量m2,交叉概率pc,变异概率pm,最大迭代次数iter_max,信息素重要程度因子α,启发函数重要程度因子β,初始化时迭代次数iter设置为1;
步骤s22,设置适应度函数,将路径长度和安全性作为主要参考指标,由于auv在航行中的威胁主要来自高度差的变化和障碍物,而在规划中路径不会与障碍物发生碰撞,因此安全性主要考虑auv的高度变化;
在auv高度不允许发生变化时,将其运动视为二维环境的运动,适应度函数只考虑路径长度最短;
在auv高度允许发生变化的情况时,将其运动视为三维环境下的运动,此时适应度函数f的表达式如下:
式中,i表示不同的蚂蚁,每只蚂蚁形成的路径一共有ni段路径。lij表示第i只蚂蚁第j段路径的长度,hij表示该段路径起点与终点间的高度差,wij为权重系数,θij表示第i只蚂蚁第j段路径的危险系数,当该段路径通过障碍物所在的栅格时,该系数取一个较大的值,反之设置为0;
步骤s23,确定解的表示形式,在算法中一条路径的解用该路径经过的栅格信息集合表示,采用区域划分的方法,可使解中的每一个栅格减少一个维度的信息,而按照步骤s12中子区域划分的方法,auv在不包含障碍物的子区间中的路径就可以只用起始和终点两个栅格表示,而在包含障碍物的子区间中再考虑用具体的栅格表示,减小了需要的栅格量,从而进一步减少了需处理和存储的数据量;
步骤s24,形成算法的初始解,在每次迭代中利用mmas算法得到路径解,蚂蚁k在栅格i选择下一个栅格j的转移公式如下:
式中,allowedk为蚂蚁k待访问的栅格的集合;
对迭代最优解对应的路径进行信息素更新,同时,在每次迭代中,计算解的平均值length_ave,全局最优解length_best和迭代最优解length_ibest;
定义判断算法转换时刻的变量length_diff1,length_diff2和length_diff3如下:
length_diff1(iter)=length_ave(iter)-length_best(iter);
length_diff2(iter)=length_ibest(iter)-length_best(iter);
length_diff3(iter)=length_ave(iter)-length_ibest(iter);
步骤s25,确定算法的转化时机iter_1,设置转化的最小迭代数iter1和最大迭代数iter2,iter_1应满足以下表达式:
iter1≤iter_1≤iter2;
步骤s26,将转化时刻mmas的路径解和此时的全局最优解作为ega算法的初始解。
所述步骤s3中利用mmas和ega算法同时进行路径寻优包括以下内容:
步骤s31,在每一次迭代中,继续按照mmas算法,更新迭代最优解所对应的路径上的信息素浓度;
步骤s32,在每一次迭代中,执行ega算法的选择、交叉和变异操作,并把得到的解保留作为下一代ega算法的初始解群,循环次数iter=iter+1;
变异算子分为两种,第一种为在解的栅格序列中随机选取两个点,将这两个栅格的位置对换,形成新的解的序列;
第二种变异算子为在解的栅格序列中随机选取两个点,将这两个栅格间的栅格按倒序排列,形成新的栅格序列;
步骤s33,将每一代ega算法得到的最优解的信息素更新;
每一次迭代中,信息素的更新由mmas和ega两种算法的迭代最优解共同更新。
所述步骤s4中利用改进的变异算子和mmas算法继续寻优包括以下内容:
步骤s41,判断算法陷入停滞状态的时刻iter_2,设置最小迭代数iter3,停滞时刻iter_2连续m次迭代和迭代次数满足以下表达式:
iter_2≥iter3;
length_best(iter_2-m)=···=length_best(iter_2-1)=length_best(iter_2);
步骤s42,将算法中蚂蚁的数量增加,以增加找到更多路径的可能性;
步骤s43,在ega算法中仅保留改进的变异算子,此时最优解已接近理论上的全局最优解,交叉操作可能会破坏已有的优良模式,因此仅保留对最优解的变异操作,且规定变异后的解得到了改进才得到保留;
步骤s44,在每5次迭代中采用作用类似于2-opt优化的变异算子,可有效改进解中交叉的路径;
为验证本发明混合算法的有效性与可行性,在cpu为i3-3220,4g内存的硬件环境下,利用软件matlab进行模拟仿真,分别在二维和三维环境下对auv路径规划的效果进行验证;
首先在25×25的二维栅格环境下,使用本发明算法,算法二和传统gaaa算法对auv进行路径规划,设定算法仿真迭代次数均为50次,实验结果如图3,图4和图5所示;
对比图3-5可知,在设置的仿真迭代次数(50次)下,本发明算法规划的路径明显短于算法二和算法三规划的路径,因此本发明算法在寻优能力上明显较优;
为验证本发明改进混合算法在不同环境下的适应性,在500×500×500的三维栅格环境下进行仿真。此环境下,本发明的混合算法与算法二和算法三寻找最优路径结果如图6所示。
为更好的说明本发明混合算法的有效性,分别对传统gaaa算法,算法二和本发明的混合算法进行30次仿真,设置仿真次数200次,将得到的结果进行对比分析,如表1-2所示;
表1为二维环境下仿真结果比较
通过表1可以看出,本发明改进混合算法优于传统gaaa算法和算法二。本发明的混合算法较传统gaaa算法和算法二在出现最优解的次数方面提高了150%和42.9%;而第一次出现最优解的迭代数则降低了31.9%和21.5%;相应的,本发明混合算法第一次出现最优解的时间缩短了35.3%和18.5%。因此,新算法不仅提高了搜索最优解的概率,还缩短了最优解搜索的时间和迭代次数。而三种算法最优解和运行时间的比较,说明了新算法虽然使得程序运行时间有所增加,但第一次出现最优解的时间仍有明显优势。
表2为三维环境下仿真结果比较
通过表2可知,三维环境下性能指标的变化与上表二维环境中的变化趋势基本一致,对比表明,本发明改进混合算法不仅收敛速度较快,寻找最优路径的概率同样较大,再次验证了本发明所提改进算法的有效性和可行性。综上说明,本发明混合算法相较现有遗传蚁群混合算法,提高了搜索效率和最优解的出现概率,得到符合最短要求的路径。
- 还没有人留言评论。精彩留言会获得点赞!