一种基于宏纤维复合材料的拉索附加弯矩减振系统的利记博彩app
本发明涉及结构工程、自动控制技术领域,尤其涉及一种基于宏纤维复合材料的拉索附加弯矩减振系统。
背景技术:
随着交通的日益发达,人们对于桥梁的跨度与舒适度也越来越高,因此斜拉桥与悬索桥对拉索的减振要求也越来越高。作为斜拉桥与悬索桥的主要承重构件之一,拉索起着传递桥面荷载的重要作用,并且拉索的特点是阻尼小,柔度大和固有频率频段较宽。这些特点使得拉索极易在外荷载或桥面桥塔的作用下产生多种振动形式。由于拉索长期处于不同振动形式作用的组合或单独作用下,拉索极可能发生疲劳破坏或者发生拉索锚固端破坏。拉索的疲劳破坏对于斜拉桥与悬索桥是致命的,这将造成严重的人员伤亡和经济损失。
关于拉索的减振策略,目前主要分为三种,空气动力学法、改变拉索自身特性与安装机械阻尼器的方法。其中,通过改变拉索自身特性来减振的方法是一种易于实现的方法,一般为辅助索法。虽然辅助索法易于布置,但辅助索减振效果受环境影响较大且不美观,因此减小外界环境对拉索的影响与改变拉索自身特性相结合的方法是拉索振动控制的重要问题之一。
宏纤维复合材料(mfc)是新型智能压电纤维复合材料,主要由三层组成,包括上下两层的交叉指型电极层与中间的压电陶瓷纤维和聚合物基质。mfc具有质量轻、韧性大、出力大、耐腐蚀性好、易于粘贴与布置等特点,具有很好的发展前景。因此结合宏纤维复合材料的韧性大、出力大、耐腐蚀性好,拉索-mfc系统将会对拉索的振动控制起到极大的作用。
技术实现要素:
基于背景技术存在的技术问题,本发明目的之一在于提供一种方法:通过对拉索轴向同位置处对称粘贴的mfc施加电压,产生与外界荷载作用引起的弯矩方向相反的附加弯矩,减小拉索承受的弯矩,从而减小拉索的振幅。
一种宏纤维复合材料的拉索,所述拉索的轴向设有若干mfc组和位移传感器,所述位移传感器连接dspace实时仿真系统的输入端,所述dspace实时仿真系统的输出端连接高压放大器的输入端,所述高压放大器的输出端连接mfc组。
优选的,所述mfc组是将若干大小相同的mfc对称地粘贴在拉索钢绞线的周围。
优选的,所述dspace实时仿真系统与计算机连接。
优选的,采用对同位置处对称粘贴的mfc施加相反方向电压的方法,从而使各mfc组产生相反方向的应变,并通过控制算法使mfc产生的附加弯矩与外界荷载产生的弯矩方向相反,构成拉索-mfc减振系统用于实时减小拉索的振幅
一种基于宏纤维复合材料的拉索附加弯矩减振系统,方法步骤如下:
s1:首先通过模态截断法大致地截取所要控制的低阶模态,以此作为确定粘贴mfc与传感器位置的预先估计;
s2:建立拉索动力学方程与状态空间方程组;
s3:由于拉索是一种频率较为密集的柔性结构,然后选用内平衡降阶方法,构造对角块占优的系统可控、可观gram矩阵,求解系统的奇异值,对比奇异值大小,若没有出现明显大于其它奇异值的情况,就增加mfc数量,直到出现远大于其它奇异值的奇异值时停止,保留奇异值较大的内平衡模态作为系统保留模态。再通过步骤二的状态空间方程与保留模态修正为基于模态坐标的状态空间方程;
s4:编写模糊pid控制算法,提取所截取模态的模态函数矩阵在传感器位置处的模态函数建立新的模态函数矩阵,并将传感器得到的物理空间信号与模态坐标信号和新的模态函数矩阵联立得到方程组,这样可以实时地求出模态坐标信号。由此实现了物理空间与模态空间的转换。通过dspace实时仿真系统输出控制信号,通过高压放大器放大电压作用于mfc,使mfc出力抵抗外界荷载作用,从而起到减振的作用。
进一步的,所述s2中拉索动力学方程与状态空间方程组的建立方法,方法步骤入下:
设e为拉索的弹性模量,i为惯性矩,s0为拉索初始索力,s为振动引起的索力增量,η为y方向的挠度,w为振动引起的y方向挠度,qx为忽略垂度影响的拉索沿水平跨长分布重量,t为时间,t为系统动能,v为系统势能,w为外力做功,m(x)为mfc产生的附加弯矩。
因为mfc对拉索的附加弯矩在拉索与mfc的横截面边界处有类似于突变的增长,且粘贴mfc的面积远小于未粘贴位置,所以mfc在除粘贴位置外的部位产生的弯矩较小,对未粘贴部位振幅的不利影响可忽略不计。
1)首先建立恒载作用下的静力平衡方程
eiη(4)-s0η″-qx=0
2)推导拉索在附加弯矩时的动力方程
根据哈密顿原理有
所以
上式的后两项与边界条件有关,其中边界的δy与δy′均为0。
所以
所以拉索的动力学方程为
3)将拉索的动力学方程写为状态空间方程的形式。
一种基于宏纤维复合材料的拉索附加弯矩减振系统统用于控制拉索的振幅。与现有技术相比,本发明具有的有益效果在于:
本发明的系统提出的基于mfc的拉索附加弯矩减振方法,将多组mfc在拉索轴向同位置处对称粘贴,通过对同位置处对称粘贴的mfc施加方向相反的电压,从而使各组mfc产生相反方向的应变,并通过控制算法使mfc产生的附加弯矩与外界荷载产生的弯矩方向相反,构成拉索-mfc减振系统以此实时地减小拉索的振幅。
本发明提出的一种基于宏纤维复合材料的拉索附加弯矩减振系统,方便实施、便于观测,提高了工作效率;该系统测试灵敏度高,能够精准调节拉索的频率。
附图说明
附图用来提供对本发明的进一步理解,并且构成说明书的一部分,与本发明的实施例一起用于解释本发明,并不构成对本发明的限制。在附图中:
图1为本发明的基于mfc的拉索附加弯矩减振系统的布置示意图,以斜拉索为例;
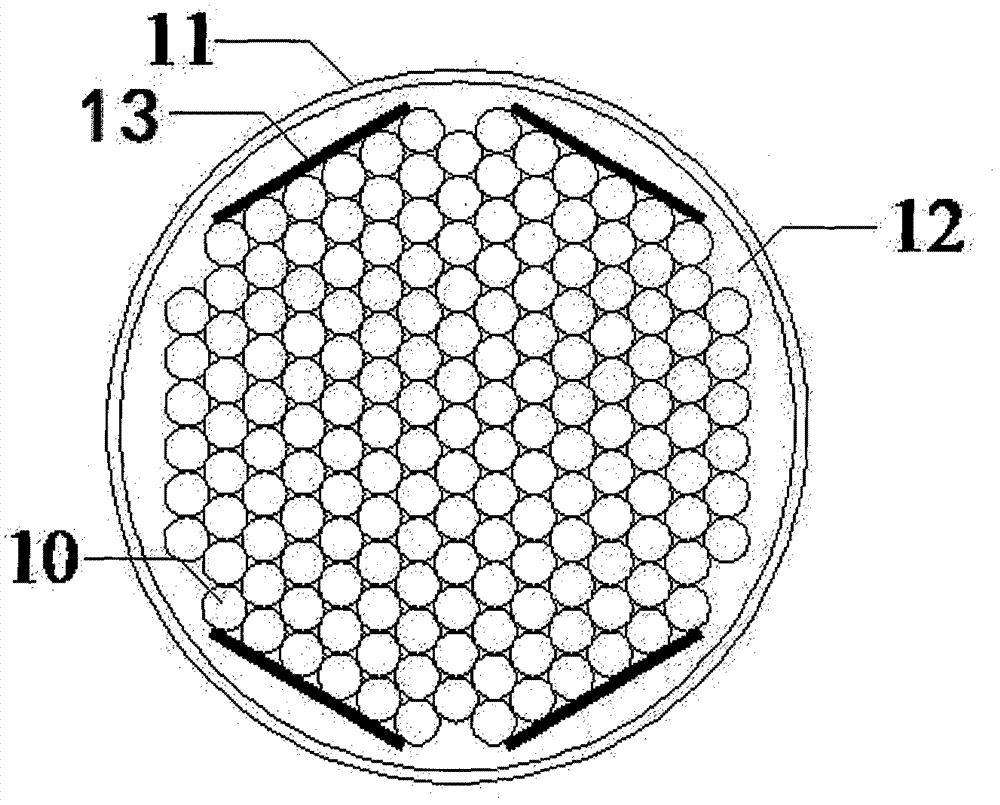
图2为本发明的mfc的粘贴位置横截面示意图;
图3为本发明的基于mfc的拉索附加弯矩减振系统的流程示意图,以斜拉索为例;
图4为基于模糊pid的拉索振动控制系统;
图5为模糊pid与pid的控制效果对比图;
图6为一阶频率下拉索的控制效果图;
图7为二阶频率下拉索的控制效果图。
图中:1-mfc组、2-拉索、3-拉索固定端、4-桥塔、5-桥面、6-位移传感器、7-高压放大器、8-计算机、9-dspace实时仿真系统、10-拉索钢绞线、11-套管、12-填料、13-mfc。
具体实施方式
下面结合具体实施例对本发明作进一步解说。
实施例1
图1表示的是基于mfc的拉索附加弯矩减振系统,在桥塔4和桥面5之间通过拉索固定端3连接拉索2,在拉索2上设有mfc组1和位移传感器6,位移传感器6连接dspace实时仿真系统9的输入端,dspace实时仿真系统9的输出端连接高压放大器7的输入端,高压放大器7的输出端连接mfc组1,dspace实时仿真系统9与计算机连接8。
实施例2
图2表示的是mfc的横向粘贴位置。在拉索钢绞线10的周围两两对称粘贴四个mfc13,拉索钢绞线10的外部设有套管11,在拉索钢绞线10与套管11之间还设有填料12。
实施例3
图3为基于mfc的拉索附加弯矩减振系统的流程示意图,(1)首先要确定mfc与传感器的粘贴位置,先通过模态截断法大致地截取所要控制的低阶模态,以此作为确定粘贴mfc与传感器位置的预先估计;(2)建立基于mfc的拉索附加弯矩的动力方程和状态空间方程;(3)由于拉索是一种频率较为密集的柔性结构,然后选用内平衡降阶方法,构造对角块占优的系统可控、可观gram矩阵,求解系统的奇异值,对比奇异值大小,若没有出现明显大于其它奇异值的情况,就增加mfc与传感器数量或改变mfc与传感器的粘贴位置,直到出现远大于其它奇异值的奇异值时停止,保留奇异值较大的内平衡模态作为系统保留模态,修正由初始估计得到的状态方程组,得到最终使用的状态方程组,此方法解决了频率密集的问题并确定了mfc与传感器的最终粘贴位置;(4)最后编写模糊pid控制算法,当有外荷载或桥塔桥面作用时,将传感器得到的物理空间信号转化为模态坐标信号,再通过dspace实时仿真系统输出控制信号,通过高压放大器放大电压作用于mfc,使mfc出力抵抗外界荷载作用,从而起到减振的作用。
实施例4
1)指定相关参数
以如图1所示的斜拉索为模型,e为拉索的弹性模量,i为惯性矩,s0为拉索初始索力,s为振动引起的索力增量,η为y方向的挠度,w为振动引起的y方向挠度,qx为忽略垂度影响的拉索沿水平跨长分布重量,t为时间,m(x)为mfc产生的附加弯矩,p(x,t)为干扰力,p0为激励力的幅值,θ为激励力的圆频率,q(t)为模态位移,v(x)为振型曲线。且粘贴mfc的面积远小于未粘贴面积,所以mfc在除粘贴位置外的部位产生的弯矩较小,对未粘贴部位振幅的不利影响可忽略不计。选用的mfc为m8514-p1型mfc,可知其长度为85mm,宽度为14mm,厚度为0.3mm,弹性模量为30.336gpa,压电常数d33为400×10-12c/n,指叉电极间距为0.35mm。本实例为粘贴5对mfc,拉索的参数为:长20m,直径25mm,初始索力为2000n,单位质量3.17kg/m,弹性模量为130gpa。
2)建立拉索动力学方程
此处使用激振器进行单点激励,假设p0为100n,激振位置为距原点位置5m处,所以取
p(x,t)=p0δ(x-0.25l)sinθt
3)列出初始条件与边界条件并求解固有频率
假设初始条件与边界条件为
v(x,0)=v0(x)
v(0,t)=0
v(l,t)=0
所以可得
w(x,t)=v(x)q(t)
分离变量得
s0v″-eiv(4)+ω2mv=0
求解可得
v=a1sin(αx)+a2cos(αx)+a3sh(βx)+a4ch(βx)
其中
代入初始条件与边界条件可得下式,求解下式得到各阶频率,由于下式为超越方程,所以只能通过数值求解解出。
2αβ(1-cos(αl)ch(βl))+(β2-α2)sin(αl)sh(βl)=0
计算得出前十阶频率
f1=0.7176hz、f2=1.4972hz、f3=2.3900hz、f4=3.4323hz、f5=4.6484hz
f6=6.0537hz、f7=7.6580hz、f8=9.4679hz、f9=11.4874hz、f10=13.7195hz
4)求解各阶振型
由此可以求解拉索的前十阶振型,可以看出拉索具有密频的特性,即一阶与二阶频率大小相差不大,因此选用内平衡降阶技术,由此可得前十阶振型。
v1(x)=x1(sin(0.176x)-0.193sh(0.913x))-0.193x1(cos(0.176x)-ch(0.913x))
v2(x)=x2(sin(0.349x)-0.363sh(0.961x))-0.363x2(cos(0.349x)-ch(0.961x))
v3(x)=x3(sin(0.518x)-0.500sh(1.035x))-0.500x3(cos(0.518x)-ch(1.035x))
v4(x)=x4(sin(0.683x)-0.606sh(1.126x))-0.606x4(cos(0.683x)-ch(1.126x))
v5(x)=x5(sin(0.846x)-0.686sh(1.232x))-0.686x5(cos(0.846x)-ch(1.232x))
v6(x)=x6(sin(1.007x)-0.747sh(1.348x))-0.747x6(cos(1.007x)-ch(1.348x))
v7(x)=x7(sin(1.167x)-0.793sh(1.471x))-0.793x7(cos(1.167x)-ch(1.471x))
v8(x)=x8(sin(1.326x)-0.829sh(1.600x))-0.829x8(cos(1.326x)-ch(1.600x))
v9(x)=x9(sin(1.485x)-0.856sh(1.734x))-0.856x9(cos(1.485x)-ch(1.734x))
v10(x)=x10(sin(1.643x)-0.878sh(1.871x))-0.878x10(cos(1.643x)-ch(1.871x))
其中
x1=0.1840、x2=0.1740、x3=0.1637、x4=0.1551、x5=0.1486
x6=0.1438、x7=0.1402、x8=0.1376、x9=0.1354、x10=0.1337
5)计算各阶模态阻尼比
由此可得到模态方程组,引入模态阻尼比
写成状态空间方程
其中
b=diag(b1b2b3…b10)
模态阻尼依靠rayleigh阻尼考虑
假设前两阶模态阻尼比为0.22%,则可得出a0与a1的值,进而求出剩余各阶阻尼比,步骤如下
由此得
可得
ξn=0.22%,0.22%,0.28%,0.37%0.48%,0.62%,0.77%,0.95%,1.15%1.37%
6)拉索的模型降阶
通过内平衡降阶技术降阶,首先求解两个李雅普诺夫方程中的wc与w0,方程如下两式
awc+wcat+bbt=0
atw0+w0a+ctc=0
然后在求解wcw0的特征值即为奇异值的平方,奇异值表征了系统模态的可控性与可观性,以此可以根据奇异值的大小来截取模态,截取奇异值较大的模态。根据奇异值的大小,这里截取前两阶模态。奇异值如下:
δ=5.602、5.577、1.287、1.281、0.394、0.392、0.145、0.144…
7)计算模态干扰力与模态控制力的大小
a)模态干扰力
0.7176hz的模态干扰力为
f1(t)=35.868sin(62.832t)f2(t)=54.849sin(62.832t)
1.4972hz的模态干扰力为
f1(t)=35.868sin(125.66t)f2(t)=54.849sin(125.66t)
2hz的模态干扰力为
f1(t)=35.868sin(188.50t)f2(t)=54.849sin(188.50t)
b)模态控制力
宏纤维复合材料的力电公式为
由于宏纤维复合材料边界处横截面的正应力一定为0,所以此处可将正应力的分布形式近似为抛物线的形式,如下所示
其中a与b分别为mfc的坐标值,d为拉索直径。
mfc附加弯矩的等效分布荷载公式如下:
由此可知弯矩二阶导数与电压之间关系为m″=3.967u,并可以计算模态控制力
其中ai1与ai2为第i片mfc的端部与尾部坐标值。
本实例为粘贴5对mfc为了有效的控制这两阶模态,将其分别粘贴在距坐标原点5m、9m、10m、11m和15m处,其中5m、9m、10m、11m处mfc的出力与15m处mfc相反,这样可以使两个模态控制都不会过小。经计算如下二式,以此作为对模态控制力的仿真限值。下面两式为
fc1=0.19122ufc2=0.24611u
传感值的求取是通过将两阶模态位移值分别乘以各自所属的振型函数得到拉索位移响应公式,再求传感器坐标下的函数值。在模糊pid控制中,通过对传感值与传感值导数的模糊化,可以调节pid参数。拉索的位移响应公式i如下:
w=v1(x)×q1(t)+v2(x)×q2(t)
8)模糊pid控制计算
本实例使用如下所示的控制系统求出拉索模态坐标下的响应,再将其转化为物理空间下的响应,本实例给出了在拉索坐标原点15m处,两个模态频率下的控制效果图与2hz作用下的模糊pid算法与pid算法的对比图,如图4所示。
从图4可以看出模糊pid控制优于pid控制,模糊pid控制控制效果更好且平稳,说明选择模糊pid算法是合适的,从图5、6可以看出mfc附加弯矩的方法有着良好的控制效果。
以上所述,仅为本发明较佳的具体实施方式,但本发明的保护范围并不局限于此,任何熟悉本技术领域的技术人员在本发明揭露的技术范围内,根据本发明的技术方案及其发明构思加以等同替换或改变,都应涵盖在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!