一种基于CompactLogix的模糊自整定PID的液位控制方法与流程
本发明属于自动控制、自动调节技术领域,具体涉及一种基于CompactLogix的模糊自整定PID的液位控制方法。
背景技术:
液位控制技术在自动化控制、自动调节系统领域有着不可替代的位置,涉及炼油、发电、化工、冶金、医药、造纸和轻工等工业部门,对国民经济的发展起着十分重要的作用。比如,锅炉的汽包水位控制,一旦液位过低,会使锅炉的温度过高而发生安全事故;供水单位的供水,如果水位过低,达不到供水的标准,对于百姓的吃水、用水会产生极大影响。总之,为确保生产的安全性和稳定性,就必须不断开发先进的液位控制技术和控制策略。
液位控制具有非线性、强耦合、大滞后、数学模型难确立等特点,使得采用常规PID控制会由于参数整定困难产生超调量大、响应速度慢、控制不稳定等问题,常规的PID控制策略已愈加不能满足工业生产的需求。由此,寻求一种适用于液位控制的PID参数自整定方法对提高液位控制的快速性、鲁棒性有着重要的意义。
技术实现要素:
本发明的目的是提供一种基于CompactLogix的模糊自整定PID的液位控制方法,解决了现有常规PID控制参数整定困难、效率低下及难以达到最佳控制效果的问题。
本发明所采用的技术方案是,一种基于CompactLogix的模糊自整定PID的液位控制方法,具体按照以下步骤实施:
步骤1:对实际液位信号y进行采样、滤波、整定和量化,然后计算设定液位信号yd与实际液位信号y间的偏差e及偏差变化率ec;
步骤2:将步骤1处理后的信号作为模糊控制器的输入量,进行模糊化、模糊推理及清晰化处理,最后得到模糊控制器的输出量ΔKp、ΔKi、ΔKd,其中,ΔKp、ΔKi、ΔKd分别为PID调节器比例增益Kp的增量、积分增益Ki的增量和微分增益Kd的增量;
步骤3:结合常规PID控制器设置的初始基准值,从而得到PID控制器的三个参数,再由PID调节器运算公式,计算控制输出,然后作用于被控对象。
本发明的特点还在于:
偏差e为:e=yd-y。
偏差变化率ec为:ec=de/dt。
步骤2具体为:
步骤2.1:确定模糊控制器的输入、输出变量的论域;
步骤2.2:模糊化,即将精确的输入变量转化为模糊量,具体为:
假设精确的输入变量x的实际变化范围为[a,b],将精确的输入变量x转换为离散论域[c,d]之间的值y:
其中,x表示输入变量,即e及ec;y表示输入变量x经过模糊化处理后所对应的模糊量;a、b分别表示输入变量x的下限与上限,c、d分别表示输入变量x经过模糊化处理后所对应输入论域的下限与上限;
如果计算出来的y值不是整数,按四舍五入的办法把它归入最接近的整数,这样就把连续量变换为离散论域中的有限整数值;
步骤2.3:定义模糊集合及其隶属度函数,其中,输入变量的模糊集合e={NB,NM,NS,ZO,PS,PM,PB},ec={NB,NM,NS,ZO,PS,PM,PB},输出变量的模糊集合ΔKm={NB,NM,NS,ZO,PS,PM,PB},m=p,i,d;
步骤2.4:建立模糊控制规律表,
ΔKp的模糊规则表如表1:
表1ΔKp的模糊规则表
ΔKi的模糊规则表如表2:
表2ΔKi的模糊规则表
ΔKd的模糊规则表如表3:
表3ΔKd的模糊规则表
步骤2.5:采用重心法对模糊控制器的输出值进行清晰化处理,具体为:
其中,zi表示第i个精确的输入变量,i=1…n,z0表示控制输出的清晰化量,μc(zi)表示输出模糊集合中的元素zi对应的隶属度函数;
步骤2.6:在Matlab环境下,利用模糊逻辑工具箱的图形用户界面建立模糊推理系统;按照步骤2.1-步骤2.5生成ΔKp、ΔKi、ΔKd的模糊控制查询表,并将查询表存储在CompactLogix控制器的内存中。
步骤3具体为:
步骤3.1:结合常规PID控制器设置的基准值,得到PID控制器的三个参数:
Kp=Kp0+ΔKp
Ki=Ki0+ΔKi
Kd=Kd0+ΔKd
其中,Kp0,Ki0,Kd0表示常规PID控制器设置的基准值;
步骤3.2:根据PID调节器运算公式,计算控制输出u(t):
然后作用于被控对象。
本发明的有益效果是:本发明一种基于CompactLogix的模糊自整定PID的液位控制方法,是一种变ΔKp、ΔKi、ΔKd的模糊PID自整定算法,它克服了变Kp、Ki、Kd模糊自整定算法对其参数选择盲目性,又兼顾常规PID和模糊控制两种方法的优点,对控制液位精度高、鲁棒性好、参数易整定,可满足更高的控制要求;同时在对象模型结构发生较大改变的情况下也能获得较好的控制效果。本发明将模糊自整定PID方法应用到水位控制算法上,将预先生成的查询表存储在CompactLogix的内存中,当进行实时控制时,便于CompactLogix的CPU根据输入信息从控制表查询所对应的控制输出量,节省计算时间,大大提高效率。与传统的PID相比较,模糊自整定PID方法对于水位控制鲁棒性更强、控制精度更高、快速性更好、参数更易整定。
附图说明
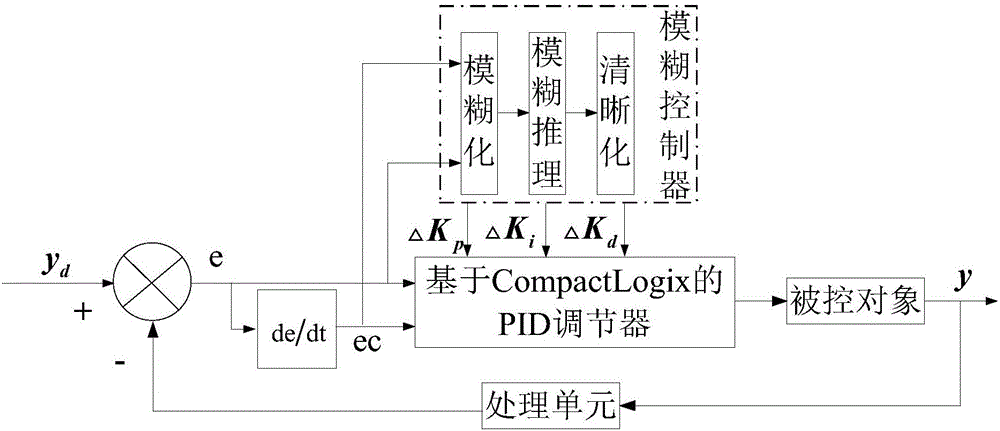
图1是本发明液位控制方法的控制结构示意图;
图2是本发明液位控制方法在PLC实现的具体流程图。
具体实施方式
下面结合附图和具体实施方式对本发明进行详细说明。
本发明一种基于CompactLogix的模糊自整定PID的液位控制方法,控制结构如图1所示,对实际液位信号y进行采样、滤波、整定和量化,然后计算设定液位信号yd与实际液位信号y间的偏差e及偏差变化率ec;将e和ec作为模糊控制器的输入变量,对输入变量进行模糊化、模糊推理、清晰化处理,得到模糊控制器的输出量ΔKp、ΔKi、ΔKd,结合常规PID控制器设置的初始基准值可得到PID控制器的三个参数,最后由PID调节器运算公式计算出控制信号,作用于被控对象。
本发明一种基于CompactLogix的模糊自整定PID的液位控制方法,具体按照以下步骤实施:
步骤1:对实际液位信号y进行采样、滤波、整定和量化,然后计算设定液位信号yd与实际液位信号y间的偏差e及偏差变化率ec;
偏差e为:e=yd-y。
偏差变化率ec为:ec=de/dt。
步骤2:将步骤1处理后的信号作为模糊控制器的输入量,进行模糊化、模糊推理及清晰化处理,最后得到模糊控制器的输出量ΔKp、ΔKi、ΔKd,其中,ΔKp、ΔKi、ΔKd分别为PID调节器比例增益Kp的增量、积分增益Ki的增量和微分增益Kd的增量;
步骤2.1:确定模糊控制器的输入、输出变量的论域;论域的选择要结合现场实际和现场经验。
步骤2.2:模糊化,即将精确的输入变量转化为模糊量,具体为:
假设精确的输入变量x的实际变化范围为[a,b],将精确的输入变量x转换为离散论域[c,d]之间的值y:
其中,x表示输入变量,即e及ec;y表示输入变量x经过模糊化处理后所对应的模糊量;a、b分别表示输入变量x的下限与上限,c、d分别表示输入变量x经过模糊化处理后所对应输入论域的下限与上限;
如果计算出来的y值不是整数,按四舍五入的办法把它归入最接近的整数,这样就把连续量变换为离散论域中的有限整数值。
步骤2.3:定义模糊集合及其隶属度函数;其中,输入变量的模糊集合e={NB,NM,NS,ZO,PS,PM,PB},ec={NB,NM,NS,ZO,PS,PM,PB},输出变量的模糊集合ΔKm={NB,NM,NS,ZO,PS,PM,PB},m=p,i,d,隶属度函数的选择是难点,要不断仿真调试,选取合适的隶属度函数曲线,才能使系统处于最优控制。
步骤2.4:根据经验知识和实验测得的数据,建立模糊规则表,ΔKp的模糊规则表如表1,ΔKi的模糊规则表如表2,ΔKd的模糊规则表如表3;控制规则的制定是关键、核心,要根据经验知识和实验测得的数据不断总结,从而得出一条条的控制规律。
表1ΔKp的模糊规则表
表2ΔKi的模糊规则表
表3ΔKd的模糊规则表
步骤2.5:通过模糊推理得到的模糊量要进行清晰化计算后才能应用于实际的控制,采用重心法对模糊控制器的输出值进行清晰化处理,虽然此方法计算量稍大,但模糊控制器的性能比较好。确立公式如下:
其中,zi表示第i个精确的输入变量,i=1…n,z0表示控制输出的清晰化量,μc(zi)表示输出模糊集合C中的元素zi对应的隶属度函数。
步骤2.6:在Matlab环境下,利用模糊逻辑工具箱的图形用户界面(GUI)可以建立模糊推理系统;按照步骤2.1-步骤2.5生成ΔKp、ΔKi、ΔKd的模糊控制查询表,并将查询表存储在CompactLogix控制器的内存中。
步骤3:结合常规PID控制器设置的初始基准值,从而得到PID控制器的三个参数,再由PID调节器运算公式,计算控制输出,然后作用于被控对象,具体为:
步骤3.1:结合常规PID控制器设置的基准值,得到PID控制器的三个参数:
Kp=Kp0+ΔKp
Ki=Ki0+ΔKi
Kd=Kd0+ΔKd
其中,Kp0,Ki0,Kd0表示常规PID控制器设置的基准值;
步骤3.2:根据PID调节器运算公式,计算控制输出u(t):
然后作用于被控对象。
具体在CompctLogix系列PLC实现具体流程如图2所示,首先将Matlab环境下生成的ΔKp、ΔKi、ΔKd的模糊控制查询表预存在CompctLogix指定内存中,根据PLC控制器扫描周期,对实时数据进行采样,之后对采样到的输入量滤波、整定和量化,从而建立输入量e、ec的模糊论域,然后对输入量e、ec模糊化,根据e、ec的模糊量确定PID参数变化量所在模糊控制查询表中的位置,查模糊控制查询表,确定ΔKp、ΔKi、ΔKd的值,结合PID调节器的三个参数的预设初值,即可得到PID调节器的三个参数,根据PID调节器运算公式,计算出的控制量直接作用于被控对象,一次控制结束。
- 还没有人留言评论。精彩留言会获得点赞!